2023年講題比賽獲獎論文之九:用思維分析揭示2023年天津卷第20題

高文娟

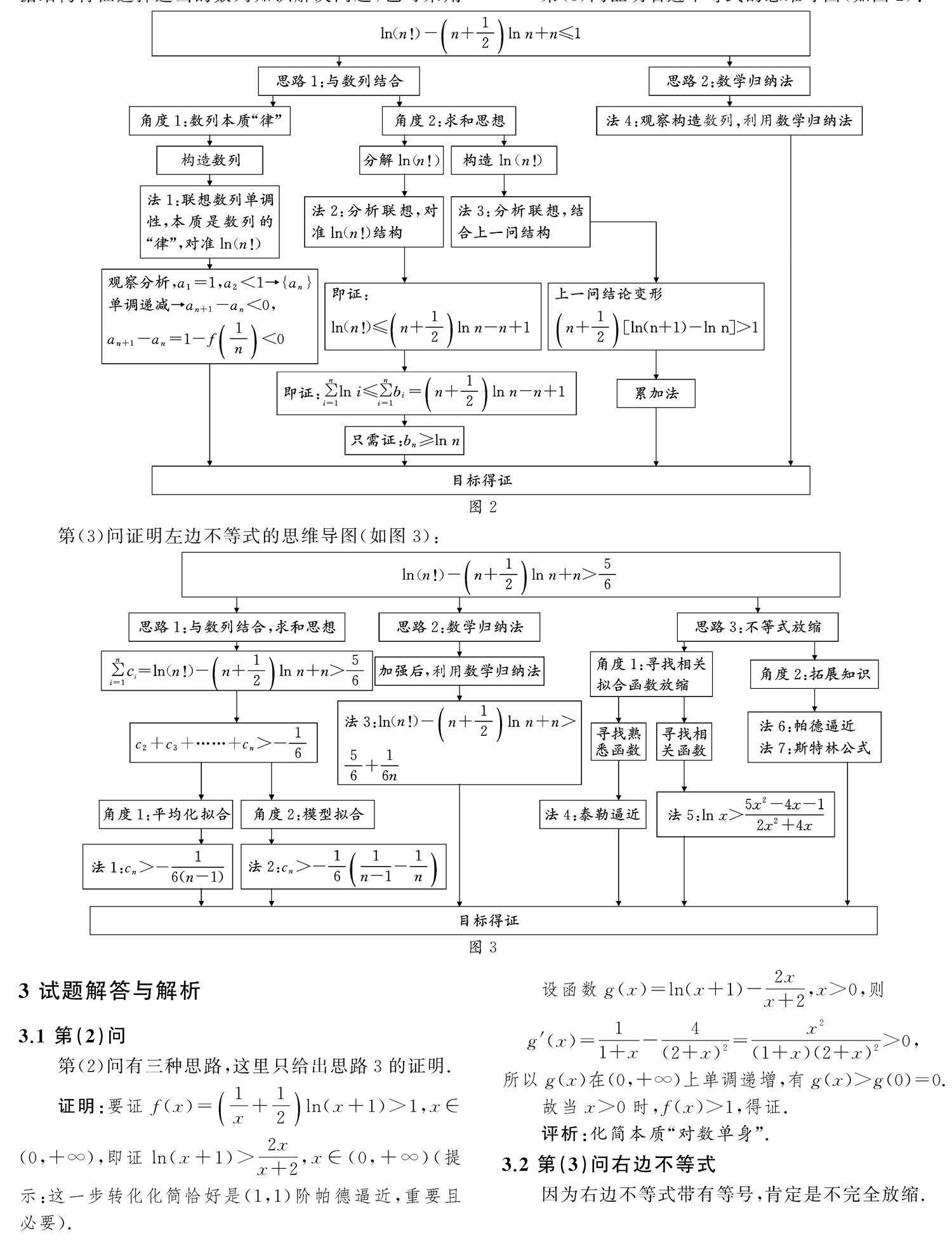
2023年天津卷第20題考查數列與不等式結構關系，運用函數思想解決問題.題目解法多樣，思維開源，充分考查學生的數學素養和思維分析能力.

1 題目：2023年天津卷第20題

已知函數f（x）=1x+12ln（x+1）.

（1）求y=f（x）在x=2處切線的斜率；

（2）當x>0時，證明：f（x）>1；

（3）證明：56

2 分析與思維導圖

2.1 思路分析

第（1）問簡單，本文從略.

第（2）問證明要觀察結構，化簡到合適結構再運算，也就是對構造函數的能力有較高要求.若令g（x）=1x+12ln（x+1）-1或g（x）=（x+2）＼5ln（x+1）-2x，則其導數中含有“ln（x+1）”，不如選擇變形為g（x）=ln（x+1）-2xx+2，這就是本題化簡的本質（“對數單身”）！這一點在以往高考題中經常出現.

本題第（3）問的命題背景源自大學數學專業《數學分析》的“斯特林公式”，但是該公式只是它的命題背景，我們無需知道，即可用高中知識解決它.當然，本題也深刻考查了學生的數學核心素養和思維分析能力.對于第（3）問：（指向最簡單與最本質的方法）觀察發現本題屬于數列型不等式，所以解答時可以結合數列知識.先看右邊不等式，要證ln（n！）-n+12＼5ln n+n≤1，

設該不等式左側為an，即證an≤1，

不難發現a1=1，則即證an≤a1，猜想an+1-an≤0，因此解題思路就出來了，證明過程用到第（2）問的結論.再看左邊不等式，不等號方向決定需要構造f（x）<1+h（x），因為要證

an-a1=（a2-1）+（a3-a2）+……+（an-an-1）=∑n-1i=11-f1i>-16，

可聯想∑n-1i=1161i+1-1i>-16，等等，也可聯想泰勒展開、帕德逼近、斯特林公式等拓展知識結論，但是都需要具體運算后才能發現是否可行.相對來講，后面給出的利用數列知識、求和思想的方法，對分析能力的要求更低，但是運算量較大.拓展知識對于培優生可以使用，但是對絕大部分學生而言，拓展知識的解法并不能讓其看到解題本質即思維的分析，所以建議教學中以初等數學知識方法為主.

2.2 思維導圖

第（2）問的思維導圖（如圖1）：

第（3）問需證明的是數列型不等式，解題時可根據結構特征選擇適當的數列知識解決問題，也可采用證明不等式問題常用的數學歸納法及放縮法.

第（3）問證明右邊不等式的思維導圖（如圖2）：

第（3）問證明左邊不等式的思維導圖（如圖3）：

3 試題解答與解析

3.1 第（2）問

第（2）問有三種思路，這里只給出思路3的證明.

證明：要證f（x）=1x+12ln（x+1）>1，x∈（0，+∞），

即證ln（x+1）>2xx+2，x∈（0，+∞）（提示：這一步轉化化簡恰好是（1，1）階帕德逼近，重要且必要）.

設函數g（x）=ln（x+1）-2xx+2，x＞0，則

g′（x）=11+x-4（2+x）2=x2（1+x）（2+x）2>0，

所以g（x）在（0，+∞）上單調遞增，有g（x）>g（0）=0.

故當x>0時，f（x）>1，得證.

評析：化簡本質“對數單身”.

3.2 第（3）問右邊不等式

因為右邊不等式帶有等號，肯定是不完全放縮.

3.2.1 法1：觀察聯想，構造數列

證明：設an=ln（n！）-n+12ln n+n，則

an+1-an=1-n+12ln1+1n=1-f1n.

由（2）知f1n>1，所以

an+1-an=1-f1n<0.

所以，數列{an}為單調遞減數列，則an≤a1=1.

故ln（n！）-n+12ln n+n≤1，得證.

評析：本質是數列的“律”，對準“ln（n！）”，如何消掉？作差.

3.2.2 法2：分析聯想，求和思想，消掉ln（n！）

證明：要證ln（n！）-n+12ln n+n≤1，即證

ln（n！）≤n+12ln n-n+1.

聯想∑ni=1ln i≤∑ni=1bi=n+12ln n-n+1.

設an=n+12ln n-n+1，則

當n=1時，b1=a1=0.

當n≥2時，

bn=an-an-1=n+12ln n-n-12ln（n-1）-1.

故bn=0，n=1，n+12ln n-n-12ln（n-1）-1，n≥2.

只需證bn≥ln n.

因為b1≥ln 1顯然成立，所以即證

n+12ln n-n-12ln（n-1）-1≥ln n，n≥2.

只需證n≥2時，有

n-12ln n-n-12ln（n-1）≥1.

只需證n≥2時，n-12lnnn-1≥1.

只需證n≥2時，n-1+12lnn-1+1n-1≥1.

即證n≥2時，f1n-1≥1.

由（2）知，不等式

f1n-1≥1顯然成立，所以有ln（n！）-n+12ln n+n≤1，得證.

評析：觀察聯想數列前n項和，利用求和思想，求出通項公式，消掉ln（n！）.

3.2.3 法3：求和思想，結合（2）的結論構造ln（n！）

證明：由（2）知f（x）=1x+12ln（x+1）>1，則

n+12ln1n+1=n+12［ln（n+1）-ln n］>1.

當n≥2時，1+12（ln 2-ln 1）>1，

2+12（ln 3-ln 2）>1，

…………

n-2+12［ln（n-1）-ln（n-2）］>1，

n-1+12［ln n-ln（n-1）］>1.

由累加法可得

n-1+12ln n-［ln（n-1）+ln（n-2）+……+ln 2］>n-1.

所以當n≥2時，n+12ln n-ln（n！）>n-1，

即ln（n！）-n+12ln n+n<1.

又當n=1時，ln（n！）-n+12ln n+n=1，

所以ln（n！）-n+12ln n+n≤1，得證.

3.2.4 法4：觀察構造數列，利用“數學歸納法”

具體過程略，可掃后面的二維碼查看.

3.3 第（3）問左邊不等式

3.3.1 法1：求和思想，平均化擬合

證明：設an=ln（n！）-n+12ln n+n.

猜想∑ni=1ci=ln（n！）-n+12ln n+n>56，

即c1+c2+……+cn>56.因為c1=1，

所以即證n≥2，c2+c3+……+cn>-16.

只需證n≥2時，an-an-1=cn>-16（n-1）.

只需證cn=1-n-1+12ln1+1n-1>-16（n-1）（n≥2）.

只需證n≥2時，有

n-1+12ln1+1n-1-16（n-1）-1<0.

令t=1n-1∈（0，1］，則只需證

ln（1+t）<16t+11t+12=t（t+6）3（t+2）.

只需證F（t）=ln（1+t）-t（t+6）3（t+2）<0，t∈（0，1］.

因為t∈［0，1］時，F′（t）=-t［（t+1）2+3］3（t+2）2（t+1）<0（運算量大！）且F（0）=0，

所以F（t）在（0，1］上單調遞減，則F（t）

評析：本方法關鍵是聯想到平均化擬合，將c2+c3+……+cn>-16轉化為通項cn>-16（n-1），化簡過程中使用了“對數單身”的化簡本質和“整體代換”的化簡技巧.

3.3.2 法2：求和思想，擬合熟悉的較簡單模型

證明：設an=ln（n！）-n+12ln n+n.

猜想∑ni=1ci=ln（n！）-n+12ln n+n>56，即

c1+c2+……+cn>56.

因為c1=1，聯想n≥2時，

c2+c3+……+cn>-161-12+12-13+……+1n-1-1n=-161-1n>-16.

只需證n≥2時，an-an-1=cn>-161n-1-1n.

只需證cn=1-n-1+12ln1+1n-1>-16（n-1）n，n≥2.

接下來整理與轉化方式同法1，略.

評析：關鍵是聯想到簡單熟悉模型進行擬合.

3.3.3 法3：加強后，利用數學歸納法

具體過程略，可掃碼查看.

3.3.4 法4：分析放縮+泰勒逼近

掃碼看附錄

秒殺法，具體過程略，可掃碼查看.

其他拓展性解法，如尋找擬合函數、帕德逼近、斯特林公式等解法不再細述，可掃碼看附錄.

4 方法延伸

解決問題的一種放縮方式：根據學生儲備知識12x-1x12x-1x進行放縮，最終的結果是an>34不夠大，進一步通過12x-1x與2（x-1）x+1的加權值調整一下，讓左側放縮結果大一點，如取12·2（x-1）x+1+14x-1x，構造函數g（x）=ln x-12·2（x-1）x+1-14x-1x，x∈（0，1），經過運算可得g（x）>0，即ln x>12·2（x-1）x+1+14x-1x，再用累加法即可得到an>78>56，得證.若取23·2（x-1）x+1+16x-1x，同理可證an>1112>56.這種構造方法學生可以掌握.

5 溯源與新題練習

5.1 溯源

（1）2022年新高考Ⅱ卷第22題：

已知函數f（x）=xeax-ex.

（ⅰ）當a=1時，討論f（x）的單調性；

（ⅱ）當x>0時，f（x）<-1，求a的取值范圍；

（ⅲ）設n∈N*，證明：112+1+122+2+……+1n2+n>ln（n+1）.

（2）2018年全國Ⅲ卷理科卷第21題：

已知函數f（x）=（2+x+ax2）ln（1+x）-2x.

（ⅰ）若a=0，證明：當-10時，f（x）>0.

（ⅱ）若x=0是f（x）的極大值點，求a.

5.2 新題練習

（1）原創命題練習

已知函數f（x）=x-aln（x+1）.

（ⅰ）當a=1時，求y=f（x）在x=2處的切線斜率；

（ⅱ）若x∈（0，+∞），f（x）>0恒成立，求a的取值范圍；

（ⅲ）證明：n∈N+，ln（n！）-nln（n+1）+n>0.

（2）2019年調研試題改編

已知函數f（x）=7+x1+x（x>0）.

（ⅰ）討論g（x）=x［f（x）］2的單調性；

（ⅱ）設a1=1，an+1=f（an）（n∈N*），試證明

2n-2|ln an-ln 7|<1.

6 結語

本題難點在第（3）問，它充分突出了數學學科的選拔性功能，深刻地考查了學生的數學核心素養和思維分析能力.具備泰勒展開等拓展知識的學生可以利用拓展知識解決問題，充分體現了數學教學的基本理念：以學生發展為本，立德樹人，提升素養，實現人人都能獲得良好的數學教育，不同的人在數學上得到不同的發展.