結(jié)構(gòu)化視角下解析幾何的教學(xué)內(nèi)容分析

虞濤 時杰

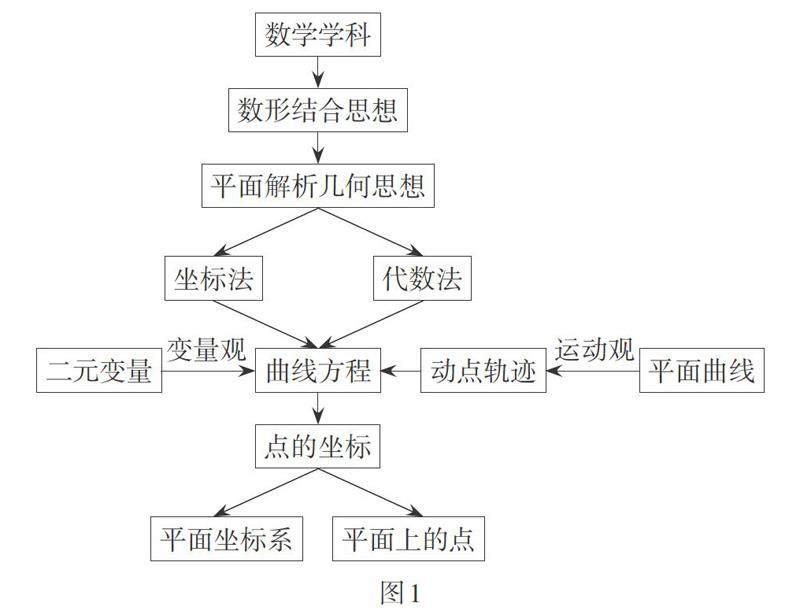
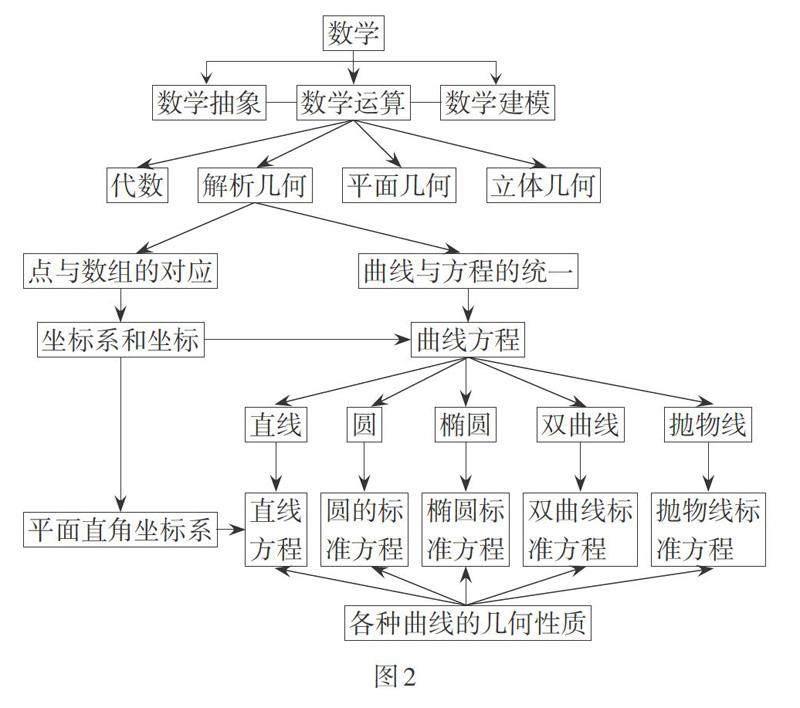
摘? 要：結(jié)構(gòu)化視角下，對中學(xué)數(shù)學(xué)教學(xué)內(nèi)容的把握需要體現(xiàn)聯(lián)系入手、整體思考和發(fā)展演繹的特點. 在此結(jié)構(gòu)下，分析了解析幾何的建立框架，包括其建構(gòu)設(shè)想、學(xué)科基石、方法精髓和教育價值，提出解析幾何的研究重點應(yīng)該包括用代數(shù)方法研究幾何問題的學(xué)科觀念、建立曲線與方程對應(yīng)的知識脈絡(luò)，以及以曲線方程和坐標(biāo)法為核心和紐帶.

關(guān)鍵詞：結(jié)構(gòu)化；解析幾何；學(xué)科框架；學(xué)科核心

中圖分類號：G633.6? ? ?文獻(xiàn)標(biāo)識碼：A? ? ?文章編號：1673-8284（2024）03-0014-05

引用格式：虞濤，時杰. 結(jié)構(gòu)化視角下解析幾何的教學(xué)內(nèi)容分析［J］. 中國數(shù)學(xué)教育（高中版），2024（3）：14-18.

課程內(nèi)容結(jié)構(gòu)化是新一輪課程改革的重要議題，《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版2020年修訂）》（以下簡稱《標(biāo)準(zhǔn)》）在“前言”關(guān)于“修訂的主要內(nèi)容和變化”中強(qiáng)調(diào)“重視以學(xué)科大概念為核心，使課程內(nèi)容結(jié)構(gòu)化，以主題為引領(lǐng)”，并在“教學(xué)與評價建議”“學(xué)業(yè)水平考試與高考命題建議”“教材編寫建議”中反復(fù)強(qiáng)調(diào). 關(guān)注課程內(nèi)容的結(jié)構(gòu)化是由數(shù)學(xué)的聯(lián)系性和整體性特點決定的. 數(shù)學(xué)的結(jié)構(gòu)是客觀存在的，只有從整體上看待數(shù)學(xué)，才能把握數(shù)學(xué)內(nèi)容的本質(zhì)，厘清中學(xué)數(shù)學(xué)課程內(nèi)容的結(jié)構(gòu)與發(fā)展脈絡(luò)，建立各條內(nèi)容主線之間的邏輯關(guān)聯(lián)，從而發(fā)展學(xué)生的數(shù)學(xué)核心素養(yǎng).

結(jié)構(gòu)化視角下對中學(xué)數(shù)學(xué)教學(xué)內(nèi)容的把握體現(xiàn)在三個方面：其一，聯(lián)系入手，站在數(shù)學(xué)知識整體的立場探尋知識產(chǎn)生的背景，捋順知識發(fā)生發(fā)展的邏輯過程和知識之間的層級關(guān)系，理解知識外在的符號表征；……