基于虛擬阻抗優化的VSG暫態功角穩定自適應控制策略

摘 要：

在電網短路故障發生的情況下，虛擬同步發電機系統不僅會發生暫態功角失穩，同時還可能會出現過流。為了提升虛擬同步發電機的暫態功角穩定性及故障電流限制性能，首先建立了包含電壓和電流控制環、虛擬阻抗及功率控制環結構的虛擬同步發電機系統的總體控制結構，給出了虛擬阻抗功率模型建立的理論依據。對無功功率控制環路惡化暫態功角穩定性，提出了設置電壓增量自由控制支路來實現提高暫態功角穩定性的方法。其次，在無功功率控制環路及電壓增量自由控制支路的共同作用下，對“不考慮切除故障”和“考慮切除故障”兩種不同的運行工況，提出了能夠同時滿足暫態功角穩定性和故障電流限制的虛擬阻抗優化方法。最后提出了虛擬同步發電機的暫態功角失穩控制和故障電流限制的自適應控制算法，以滿足實際運行工況的需求，通過Simulink仿真模型驗證了所提自適應控制策略的有效性和可行性。

關鍵詞：虛擬同步發電機；同步穩定性；等面積法則；虛擬阻抗；故障電流限制；李雅普諾夫穩定性

DOI：10.15938/j.emc.2024.01.004

中圖分類號：TM46

文獻標志碼：A

文章編號：1007-449X（2024）01-0035-14

Improvement of transient stability performance of VSG considering power angle stability and fault current limiting

SUN Jiuliang，"CAI Wei，"GUO Qingbo

（School of Electrical and Electronic Engineering， Harbin University of Science and Technology， Harbin 150080， China）

Abstract：

In addition to transient power angle instability， the virtual synchronous generator system may also experience overcurrent in the event of a grid short circuit fault. In order to improve the transient power angle stability and fault current limiting performance of VSG， firstly， the overall control structure of virtual synchronous generator system including voltage and current control loop， virtual impedance and power control loop structure is established in this paper，the theoretical basis for establishing a virtual impedance power model is provided. Due to the activation of reactive power control loop， transient power angle stability will be reduced， a method of improving the power angle curve by setting the free control branch of the voltage increment is proposed. Secondly， with the combined effect of the reactive power control loop and the voltage increment free control branch， a virtual impedance optimisation method that can simultaneously satisfy transient power angle stability and fault current limitation is proposed for two different operating conditions， namely “without considering fault removal” and “considering fault removal”. Finally，adaptive control algorithms for transient power angle instability control and fault current limitation of virtual synchronous generators are proposed to meet the requirements of real operating conditions. The validity and feasibility of the control strategy proposed in this paper are verified by the simulation model.

Keywords：virtual synchronous generator; synchronous stability; equal area rule; virtual impedance; fault current limitation; Lyapunov stability

0 引 言

隨著“雙碳”戰略的提出和實施，以風力、光伏為主導的大規模的清潔型能源（新能源）所產生的電能將會通過并網變流器流向電網。以同步發電機為主體的傳統電力系統將會逐漸被以變流器為并網接口的新能源所替代[1]。目前，并網變流器通過鎖相環（phase locked loop，PLL）與電網保持同步的運行方式還處于主導地位，其優勢在于通過使用最大功率跟蹤（maximum power point tracking，MPPT）控制器可以使系統輸出最大功率[31-32]。然而，由于其本身不具備慣性及阻尼特性，大規模的使用將會導致電網的慣性降低、阻尼變弱。除此之外，當交流電網的短路比（short circuit ratio，SCR）接近13時，由于PLL的負面影響，基于PLL同步型的并網變流器難以保證其控制穩定性[2-3]。同時，受功率半導體器件過載能力的限制，變流器過載能力相對較弱。上述差異性對電力系統的穩定運行帶來了新的挑戰。

針對電力系統存在的低慣性、弱阻尼的特征。目前，面對分布式電源接入的微電網系統，具備組網能力的虛擬同步發電機（virtual synchronous generator，VSG）技術逐漸成為一種可行的解決方案，理論上這一技術可以使微電網當中的并網變流器表現出和傳統同步發電機（synchronous generator，SG）完全相同的外特性。同時，這種控制策略使并網變流器能夠在超弱交流電網下穩定運行，SCR幾乎等于1[4]。

從目前看來，VSG要比SG更加靈活可控，可以通過對控制算法的優化進一步提升小信號穩定性，進而提高虛擬同步發電機在慣性提供、調頻和調壓方面的性能。隨著基于線性系統理論（如特征值和頻率分析）工具應用的成熟，VSG的小信號穩定性已從不同方面進行了廣泛研究，如小信號動態特性、與SG的差異、建模和參數設計、具有改進小信號穩定性的新型VSG等。然而，小信號穩定性是實現暫態功角穩定的必要條件，而不是充分條件。

在大信號穩定性的研究工作范疇當中，作為一種功率同步型變流器控制技術，盡管文獻[5-6]證明了組網控制比跟網控制在弱電網中表現出更好的暫態功角穩定性。并且文獻[7]已經證明了基于下垂控制的并網逆變器的暫態功角穩定性要強于同步發電機。然而，由于其不能為電網提供慣性，這可能會對高滲透率的電網穩定性帶來嚴重挑戰。由于虛擬同步發電機與同步發電機工作原理的相似性，虛擬同步發電機在嚴重故障下同樣面臨過流的風險和功率振蕩[8-13]。因此，隨著虛擬同步發電機技術在逆變器控制技術方向上的發展，其暫態功角穩定性的研究工作變得越來越重要。

在以往的針對VSG的暫態功角穩定性的研究工作內容當中，不僅涉及到不同類型虛擬同步發電機的暫態功角穩定性問題[14-16]。而且也關注了環路參數對暫態功角穩定性的影響，同時也有考慮到有功功率環和無功功率環結構的不同對VSG的暫態功角穩定性的影響[5-6，17-20]。比如，文獻[20]研究了慣量對暫態功角穩定性的影響，發現大慣量有利于首擺穩定性，但不利于全局穩定性，配置合適的慣量有助于平衡VSG的首擺穩定性和全局穩定性。文獻[18]已經證明了在低慣量和弱阻尼條件下，轉矩形式的有功功率控制環路比功率形式的有功功率控制環路具有更好的穩定性，且兩者的差異隨著慣量的增大而減小。又比如，由于在電網電壓跌落時，變換器端電壓與電網電壓的相角差將導致輸出無功功率突增。由無功功率環路下垂關系可知，輸出無功功率增加將導致參考電壓幅值的下降，并同時帶來變換器輸出有功功率的減小，加劇了故障期間變換器輸出有功功率和參考有功功率的不平衡，導致無功功率控制環路會對暫態功率角穩定性產生“惡化效應”[17]。因此，在分析VSG系統的暫態功角穩定性時，無功功率環路不可以忽視，因為當系統發生大擾動時，VSG的無功功率環路會影響電壓指令值的幅值。盡管文獻[30]提出了基于無功功率控制環路頻率前饋的暫態功角穩定性提升方法。文獻[20]提出了通過將角加速度的動態引入到無功功率控制環路中，通過提高功角曲線來提高暫態功角穩定性的方法。然而，由于兩者對電壓指令增量沒有建立約束條件，由此可能產生的過流問題并未得到認識和解決。

在以往的研究工作內容當中，虛擬阻抗被認為是一種很好的限流措施，并且可以實現動態調整，可以對功率響應特性和穩定性的提升起到重要作用。因此，可以通過設計虛擬阻抗來重塑VSG輸出阻抗，進而提高VSG的穩定性。然而，如果輸出阻抗的設計僅基于小信號穩定性分析。在大擾動發生的情況下，僅能滿足小信號穩定性約束的輸出阻抗不能保證系統的安全、穩定運行。

由于大擾動類型的故障（如短路故障和線路跳閘）會導致過電流和暫態功角失穩等問題。文獻[21]建立了包括虛擬阻抗在內的簡化成網模型，并揭示了虛擬阻抗會危害功角穩定性，但動態性能和響應是未知的。文獻[19]分析了不同結構的虛擬阻抗在電磁暫態過程中的動態性能，在電壓指令恒定的條件下，對于I型擾動和II型擾動發生的情況，建立了同時滿足電流限制約束和李亞普諾夫穩定性條件的虛擬阻抗邊界。因此，在此基礎之上，無功功率控制環路對暫態功角穩定性和過流的影響需要被考慮。

針對上述問題，首先近一步分析和考慮VSG的無功功率控制環路對暫態功角穩定性和過流的影響，通過設置不帶增益系數的電壓增量自由控制支路來實現功角曲線的抬升，進而提升暫態功角穩定性。其次，在電壓增量沒有建立約束條件的情況下，針對“不考慮切除故障”和“考慮切除故障”兩種不同的運行工況，建立能夠滿足電流限制條件和李雅普諾夫穩定性條件的虛擬阻抗約束條件。提出滿足VSG的暫態功角失穩控制和故障電流限制的自適應控制算法。最后，通過Simulink仿真模型驗證了本文所提自適應控制策略的有效性和可行性。

1 模型的建立及分析

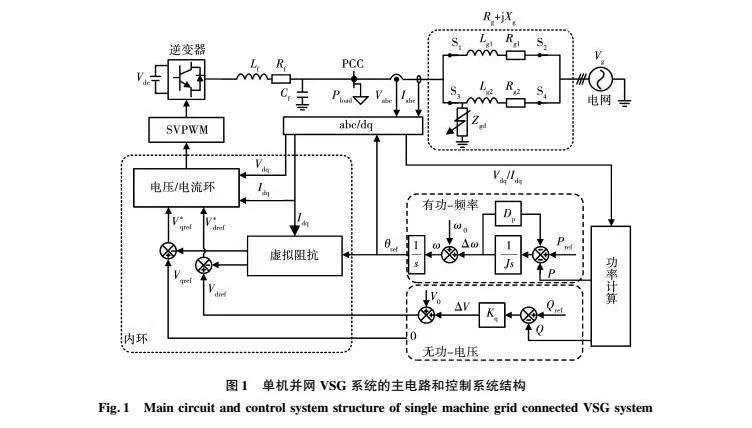
目前，由于單機無窮大系統已經成為暫態同步穩定研究工作的基礎。因此，本文在基于dq軸旋轉坐標系的控制框架下，建立了如圖1所示單機無窮大三相并網VSG系統的主電路和控制系統結構。

由于文獻[7]已經指出其暫態特性取決于故障期間的運行場景（是否有平衡點，是否觸發電流限制），而不是具體的故障類型。因此，可以采用輸電線路的三相短路故障模擬不同的故障運行場景。其中：Rg、Lg分別表示的是線路的電阻和電感，Vg表示電網的電壓，兩者共同構成電網的戴維南等效電路；S1～S4表示斷路器；Rg1～Rg2表示線路電阻；Lg1～Lg2表示線路電感；Lf、Rf、Cf表示濾波器的電阻、電感和電容；Iabc是注入電網的電流矢量；Vpcc是PCC（公共耦合點）點的電壓；VSG輸出的有功功率在本文中用P表示，無功功率用Q表示，其參考值分別用Pref和Qref表示。由于直流測電壓通常由儲能變流器控制，在分析VSG的暫態功角穩定性時，可以認為直流測電壓是恒定的。有功功率控制環提供角度參考值，無功功率控制環提供電壓幅值的參考值。

1.1 控制環路模型

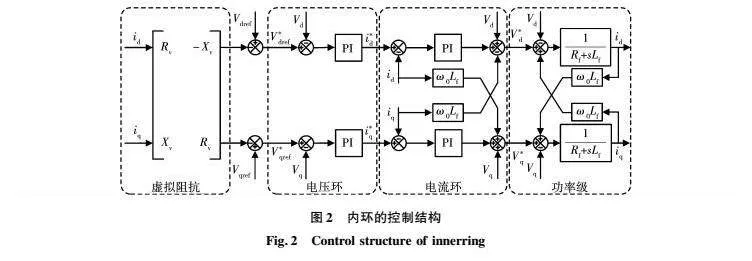
內環控制部分具體內容如圖2所示，虛擬阻抗采用虛擬復阻抗，電壓控制環路和電流控制環路均采用比例積分（proportional integral，PI）控制器。值得注意的是，內環控制的時間尺度通常與外環控制的時間尺度存在數量級差別[13]。因此，由于他們存在時間尺度解耦，這2個環路的動態特性可以進行獨立分析[14]。同時，由于電壓環和電流環控制的引入，逆變器的等效阻抗和內部電壓發生了變化，將會有助于暫態功角穩定性的提升[17-22]。

在有功功率控制環路中，ω被定義為VSG的角頻率，在此基礎之上，可以很容易推導出ω=ω0+Δω。由此，得到如下的有功功率控制律：

其中J和Dp分別表示虛擬慣量和調速器的增益。通過降低有功參考值Pref，在提高暫態功角穩定性的同時，降低了系統的頻率穩定性。因此，應當盡量避免采取這一措施。

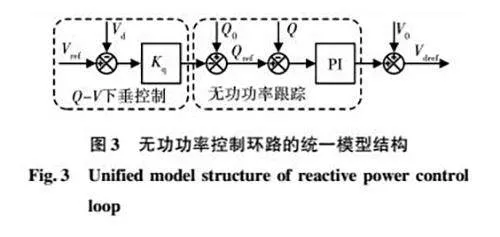
由于VSG的虛擬慣量與同步發電機的慣量實際作用效果存在明顯差距，導致頻率和電壓控制效果存在較強的時間尺度上的耦合，無法忽略無功功率控制環路對暫態功角穩定性的影響[29]。為了研究不同的無功功率控制環路對暫態功角穩定性的影響，可以應用等面積法則（equal area criterion，EAC）函數和李雅普諾夫函數對VSG的暫態功角穩定性進行分析的無功功率控制環的統一模型結構被建立[20]，如圖3所示。基于所提出的統一模型，可以分析驗證不同無功功率控制環對VSG的暫態功角穩定性的影響。

盡管Q-V下垂控制對VSG的暫態功角穩定性的作用更加靈敏，然而，無功功率下垂系數Dq對VSG的暫態角穩定性的影響受Vd和Vref的狀態的影響。隨著電壓指令Vref、參考無功功率和電容電壓的增加，加速面積減小，減速面積增加。相反，隨著電壓指令Vref的減小，加速面積增加，減速面積減小。除此之外，無功功率控制環的響應速度與暫態功角失穩問題的時間尺度存在數量級差別，可以認為在故障發生后，無功功率控制環能夠快速響應至穩態，因此，從這個角度來看，Vdref可以被視為一個參數變量，而不是作為一個狀態變量來處理。

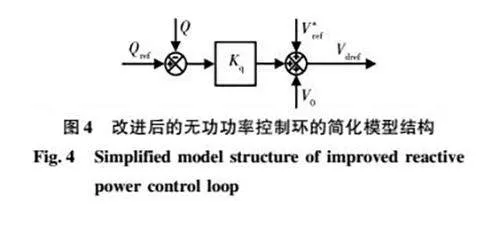
綜合考慮上述因素，本文提出通過設置電壓增量的自由控制支路來提高暫態功角穩定性的控制方法，如圖4所示。其中Kq是無功功率的控制器增益，其控制律為

值得說明的是，Vref的增量大小如何設置將會在第3部分內容當中具體給出。

1.2 虛擬阻抗功率模型

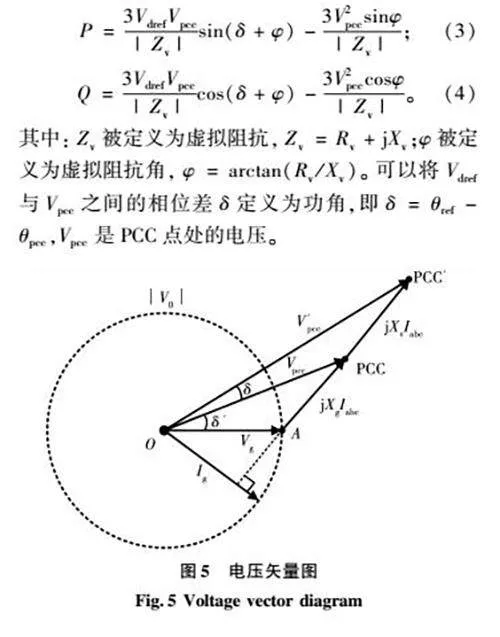
在不計濾波器阻抗、電網電阻Rg和虛擬電阻Rv的情況下，以電網電壓Vg為參考向量，VSG的電壓矢量圖如圖5所示。其中：PCC′是虛擬公共耦合點；δ′是Vg和Vpcc之間的相位差；δ是V′pcc（Vdref）和Vpcc之間的相位差；V′pcc是虛擬公共耦合點處的電壓。根據電壓矢量圖可以發現δ′和δ同時穩定。如果δ′不穩定，δ就會發生振蕩。因此，δ可以表征系統在PCC點電壓驟降下的動態性能，也就是說可以表征VSG系統的暫態功角穩定性，這一發現為功率模型的建立奠定了理論基礎。在此基礎之上，根據圖1及線路功率傳輸原理，VSG的輸出有/無功功率可以建模如下：

其中：Zv被定義為虛擬阻抗，Zv=Rv+jXv；φ被定義為虛擬阻抗角，φ=arctan（Rv/Xv）。可以將Vdref與Vpcc之間的相位差δ定義為功角，即δ=θref-θpcc，Vpcc是PCC點處的電壓。

2 虛擬阻抗約束條件及穩定性分析

2.1 Ⅰ型擾動：平衡點存在

暫態功角穩定性分析工作的主要難點在于提取其大信號的非線性動態響應。由于小信號建模方法和線性控制理論已不適用，通常基于非線性微分方程的理論分析又是一項非常繁瑣的工作。因此，本文采用等面積法則和相位圖相結合的方法進行暫態功角穩定性分析。

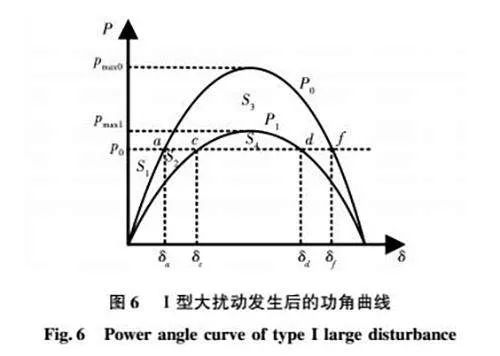
在不考慮阻尼影響的情況下，Ⅰ型大擾動發生后的功角失穩機理可以在基于等面積法則理論的基礎之上用圖6所示的功角曲線解釋，其中實線P0為擾動發生前的功角曲線，其最大輸出功率極限幅值為pmax0，a、f分別為其平衡點和不平衡點，δa和δf為對應的功角，并且δf=π-2φ-δa，減速面積S3（由曲線P0和p0的a、f段包圍的區域）將大于加速面積S1（由曲線P0和p0的0、a段包圍的區域）。其中實線P1為擾動發生后的功率角曲線，其最大輸出功率極限為pmax1，c、d分別為其平衡點和不平衡點，δc和δd為對應功角，由于減速面積S4（由曲線P1和p0的c、d段包圍的區域）將小于加速面積S1+S2的出現，導致功角將會越過δd（不穩定平衡點，有的文獻當中也稱之為最大臨界點），出現功角震蕩失穩。

假設在利用電壓增量的自由控制支路動態調整電壓指令的基礎之上，通過對VSG的虛擬阻抗進行優化，為阻抗優化設計準則，能夠正確響應PCC點電壓和電流的變化，那么電磁暫態過流和暫態功角穩定性問題就有期望能夠同時得到解決。

由于在大擾動發生后，電壓、電流控制環路會出現最快的動態響應過程，因此，可以將故障發生后的電壓指令的初始值Vdref0用于計算限流阻抗的邊界。如果在電壓、電流的動態變化過程中，忽略電壓、電流控制環路的延遲所造成的影響。在dq軸坐標系當中，VSG的輸出電流可以用下式表示：

其中：|Zv|表示阻抗的模值；δ0可以通過后文計算得出。如果PCC點的電壓從V0下降到Vsag，在dq軸坐標系當中，VSG的輸出電流的d軸和q軸分量可以分別寫為：

根據Park反變換，可以很容易得到α-β參考坐標系中α軸的電流iα，即

通過求解式（7）的極大值可以獲得電流的最大值，最大值的求解如下：

通過對式（7）求導數獲得最大電流出現的時刻tmax，具體如下：

在確定電流極限值Imax以后，Imax值的選取主要取決于所采用的功率半導體器件的電流極限，一般在實際工程當中最低也要保持15IN的裕度。由此，可以導出限流阻抗的邊界如下：

本文的貢獻在于經過研究發現，在無功功率控制環路和不同結構的虛擬阻抗結構作用下，文獻[19]當中提出的限流虛擬阻抗模型仍然適用。值得說明的是，為了保證穩態裕度，虛擬阻抗應當盡可能的小，這也就對功率器件的過流能力提出了更高的要求。

由于穩定平衡點處和不穩定平衡點處Δω=0。因此，在式（12）的基礎之上，令Δω=0，可以推導出穩定平衡點處的功角如下式：

為保證平衡點的存在，穩定平衡點處的功角δa必須滿足下式條件：

從式（13）中可以看出，隨著虛擬阻抗、PCC點電壓及電壓指令值的變化，穩定平衡點和不穩定平衡點也將隨著發生變化。同時，在Ⅰ型擾動發生后，穩定平衡點和不穩定平衡點仍然可以確定。而且，在式（13）和式（14）的基礎之上，將大擾動發生后的相應變量代入其中，便可導出大擾動發生時平衡點存在的虛擬阻抗邊界為

根據式（1）和式（3），在不考慮阻尼效應的情況下，大擾動發生后的VSG的轉動方程可以用下式表示：

如圖6所示，假設電壓指令此時是一個定值，大擾動發生后的平衡點為（δc，Δω=0），將式（16）從這一點開始積分，可以得到如下函數：

從中不難看出，式（17）當中的函數是一個具有明確物理意義的函數，可以準確描述功率波動過程中動能Ek與勢能Ep之間的轉換，因此，在后面的分析中可以被當作李雅普諾夫能量函數來使用[19，24]。

值得注意的是，在考慮電壓動態變化時，重新構建李雅普諾夫函數有一定的難度。為此，如果將電壓指令值不再作為狀態變量，而是作為參數變量，這一問題就可以得到解決。當確定某一參數變量Vdref，虛擬阻抗的邊界就可以確定，而隨著狀態變量的改變，參數變量Vdref同樣會改變，因此需要根據系統此時刻的運行狀態求解下一時刻的參數變量Vdref，進而確定下一時刻的虛擬阻抗邊界。

在Ⅰ型大擾動的情況下，將初始點（δa，Δω=0）代入式（17），可得初始能量V（δa，0）為

不穩定平衡點為（π-2φ-δc，Δω=0），因此，類似地，臨界能量Vcr可導出為

根據李雅普諾夫穩定性判據，暫態功角穩定的虛擬阻抗邊界可由下式確定：

此外，為了保證VSG在故障清除后仍然穩定運行，即當終端電壓恢復到正常水平時，平衡點仍應存在，與式（15）類似，虛擬阻抗應當滿足式（21）的條件。

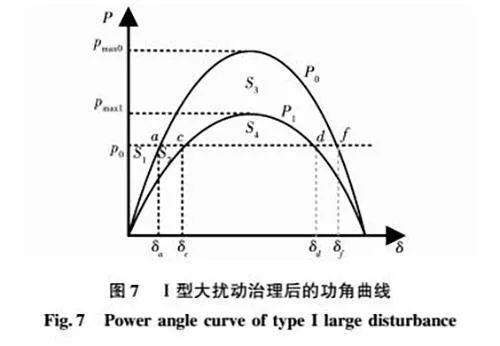
經過提出的控制策略治理后的功角曲線如圖7中實線P1所示，c、d為其平衡點和不平衡點，δc和δd為對應功角，減速面積S4將大于加速面積S1+S2。

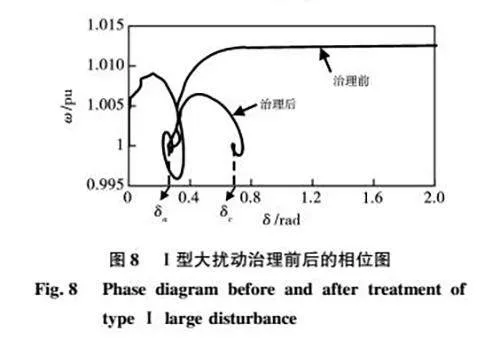
對于Ⅰ型擾動發生的情況，在Simulink仿真模型運行的過程中，提取出的相位圖如圖8所示。在故障發生時刻前，不管是經過治理的VSG系統和沒有經過治理的VSG系統，平衡點都是（δa，Δω=0）。在故障發生后，沒有經過治理的VSG的功角和頻率一直增大，直到超出不穩定平衡點。然而，經過治理的VSG的頻率和功角在經過一段時間波動以后，重新穩定在一個新的平衡點（δc，ω0）。

2.2 Ⅱ型擾動：平衡點不存在

2.2.1 不考慮切除故障

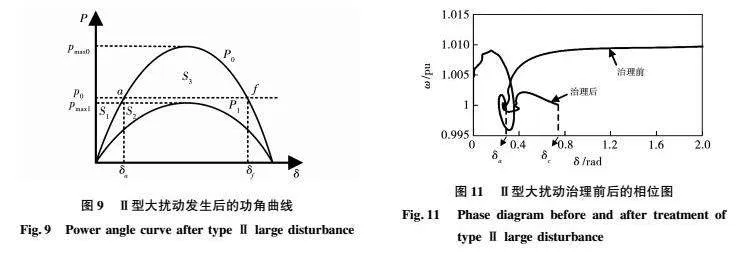
在三相短路故障發生期間，由于斷路器故障或其他原因，可能會導致故障無法被切除，在這種情況下，仍然需要保證VSG系統與電網保持同步運行。如圖9所示，在不考慮阻尼影響的情況下，Ⅱ型大擾動發生前的功角曲線為P0，大擾動發生后的功角曲線為P1，加速面積為S1+S2，減速面積為0，由于p0gt;pmax1，導致ω·gt;0，VSG的輸出頻率ω會一直處于增大的狀態，功角δ也會一直增大，直至出現功角失穩狀態。在這種情況下，VSG系統必須迅速采取措施保持穩定。如果要求在故障期間保持一定時間的穩定運行，那么就需要恢復平衡點。

針對平衡點不存在的情況，受文獻[28]中恢復平衡點的思想啟發。在不考慮切除故障的情況下，本文提出通過主動改變電壓指令、功率指令調整的綜合治理方法使平衡點恢復。同時，在平衡點恢復后，可以再次通過式（10）、式（15）、式（20）和式（21）確定新的阻抗邊界。此外，本文提出了適用于新型控制策略的迭代算法，詳細內容可見第3節所述。

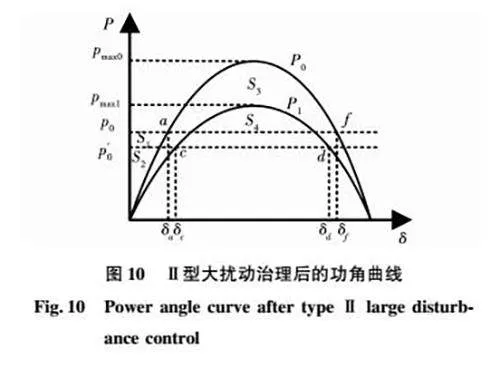
經本文所提出的控制策略治理后的VSG的功角曲線如圖10中實線P1所示，c、d為對應的其平衡點和不平衡點，δc和δd為對應的功角，減速面積S4將大于加速面積S2。

對于Ⅱ型擾動發生的情況，在Simulink仿真模型運行的過程中，提取出的相位圖如圖11所示。在故障發生時刻前，不管是經過治理的VSG和沒有經過治理的VSG，平衡點都是（δa，Δω=0）。在故障發生后，沒有經過治理的VSG的功角和頻率一直增大，直到超出最大臨界點。然而，經過治理的VSG的頻率和功角在經過一段時間波動以后，重新穩定在一個新的平衡點（δc，Δω=0）。

2.2.2 考慮切除故障

由于微電網的短路故障保護有一個快速反應時間，這個反應時間依賴于參數設置，同時也可能會與控制器及斷路器的反應時間相關。因此，從短路故障發生到短路故障線路被切除會需要一定的時間才能完成。而且必須在越過不穩定平衡點之前，確保故障被切除。除此之外，在考慮切除故障情況下，可以利用擴展的等面積法則理論對暫態功角穩定性進行分析。

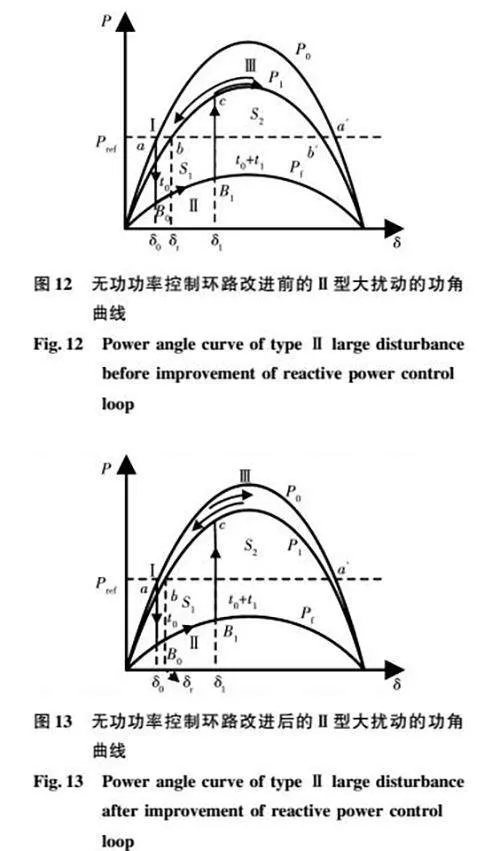
在考慮切除故障的情況下，Ⅱ型大擾動發生的整個物理過程按照時間順序可以被分成第Ⅰ、Ⅱ及Ⅲ階段，如圖12所示。假設擾動發生在t0起始時刻，那么在t0時刻以前，VSG系統一直處于穩定運行狀態，其中：a（δ0，Δω=0）點為穩定平衡點，a′（π-2φ-δ0，Δω=0）為不穩定平衡點，這一階段被定義為第I階段。在t0時刻發生大擾動，運行點從功角曲線P0上的點a下降到功角曲線Pf上的點B0。由于Prefgt;Pf，導致dω/dtgt;0，功率指令和功率輸出表現為不平衡，頻率和功率角開始增大，直到繼電器動作切除故障線路。從大擾動發生到故障清除這一階段被定義為第Ⅱ階段。在t0+tf及以后時刻，故障被切除后，如果在無功功率環路不采用所提控制策略的情況下，由于雙回線路變成單回線路，線路阻抗變大，PCC點電壓回不到額定值。因此，功角曲線一般不會快速重新回到功角曲線P0，此時的功角曲線P1會低于功角曲線P0。此外，由于c點遠離b點，在S2gt;S1的前提條件下，即減速區域面積大于加速區域面積，功角會經過一個動態振蕩過程之后，最終穩定在b點。相反，如果無功功率控制環路采用所提控制策略，功角曲線則會提高，并且有希望快速重新回到P0。隨著功角曲線被提高，加速面積減小，減速面積增大，更有利于功角穩定，如圖13所示。

在第Ⅰ階段，在t0時刻及以前，VSG系統以穩態運行情況下的虛擬阻抗Zs工作在穩定平衡點a，在平衡點a處，VSG的轉動方程可以描述為

其中|Zs|和φs分別是穩定運行態運行狀態下使用的虛擬阻抗的幅值和阻抗角。由于這一階段的狀態變量可以作為第Ⅱ階段的初始條件。因此，根據式（13），平衡點a（δ0，Δω=0）處的功角δ0的表達式可寫成如下形式：

同樣，為保證平衡點的存在，穩定平衡點處的功角δ0必須滿足如下條件：

在第Ⅱ階段，在t0時刻至t0+t1時刻這一時間段內，由于電網三相短路故障會導致Vpcc的幅值瞬間大幅降低，無功功率控制環路來不及響應，如果虛擬阻抗仍然保持著Zs，則會出現非常大的電磁暫態電流。因此，需要確定限流虛擬阻抗的邊界Zf。參照Ⅰ型擾動發生過程中限流阻抗邊界的確定方法，限流阻抗邊界條件如下：

在第Ⅲ階段，由于第Ⅱ階段的結束狀態B1是第Ⅲ階段的初始狀態。在點B1處的狀態變量，即功率角δ1和角頻率偏差Δω1，可以通過使用鎖相環測量獲得，用于評估第Ⅲ階段的暫態功角穩定性。當故障線路被切除后，Vpcc會快速恢復。假設恢復后的電壓為Vpost，則轉動方程可以用下式表示：

其中|Zr|和φr分別表示第Ⅲ階段特定的虛擬阻抗幅值和阻抗角。

為了評估系統是否能再次實現漸近穩定，類似于前面對Ⅰ型大擾動的分析，采用了李雅普諾夫穩定性定理。如前所述，李雅普諾夫能量函數可以寫成如下形式：

其中δr為電壓恢復后的穩定平衡點對應的功角，可通過替換式（13）中的相關變量計算得到。

將這一階段的不穩定平衡點（π-2φr-δr，Δω=0）和B1（δ1，Δω1）代入到式（28），可得到臨界能量值Vcr和初始能量值V（δ1，Δω1）。然后，根據式（17）描述的李雅普諾夫穩定性標準，類似于式（19）的推導，最終可得到滿足功角穩定性的虛擬阻抗邊界，即

與文獻[19]相比，本文的貢獻在于經過研究發現，在無功功率控制環路的作用下，將電壓指令值不再作為狀態變量，而是作為參數變量處理，避免了重新構造李雅普諾夫函數。并且將I型擾動的虛擬阻抗優化模型擴展到了Ⅱ型擾動的不考慮切除故障類型當中。除此之外，將故障線路切除后，功角曲線降低的情況考慮其中。因此，本文的目的是通過虛擬阻抗優化對建立電壓增量的自由控制支路的無功控制環路提供約束條件。

3 自適應電壓和虛擬阻抗控制

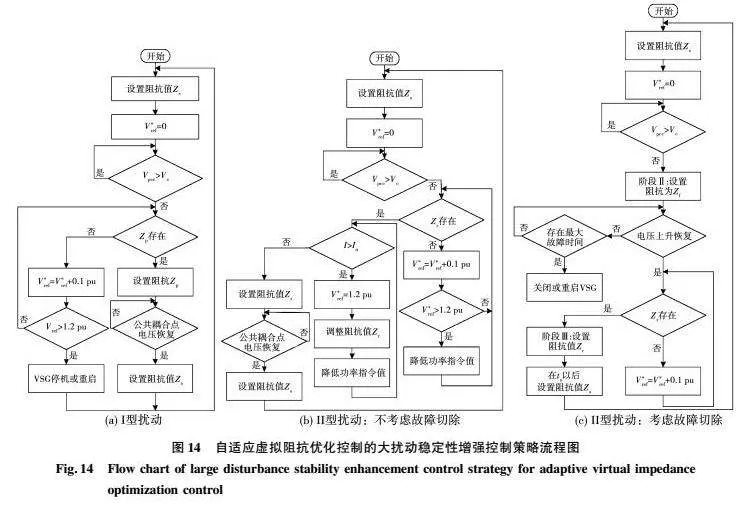
在不同的應用工況條件下，為了獲得更好的動態性能，必須優化控制參數。為此，在上述理論分析的基礎之上，提出一種自適應的虛擬阻抗和電壓優化控制策略。首先，應當時刻檢測公共耦合點電壓，一旦出現電壓值低于09 pu的情況，則會進入故障分類、處理階段。如上所述，根據大擾動的類型Ⅰ和類型Ⅱ，將控制程序分為兩種情況分別處理。為了區分這兩種情況，應導出它們之間的臨界電壓邊界Vc，如下式所示：

邊界位于功率基準線與功率角曲線相切的位置，如圖9所示。

如果Vpccgt;Vc，表示擾動屬于I類大擾動，如圖14（a）所示，則將從預先制作的查找表中選擇大擾動期間的虛擬阻抗，該表由Zp表示。如果電網較弱，Zp可能會不存在，需要動態提高逆變器的電壓指令值，電壓指令值變化的步長不易過大或過小，步長過小則收斂速度變慢，步長過大會跨越最優動態電壓值達到極限值，本文設定步長為01 pu，經過仿真驗證實際可行。在提高電壓指令后，需要重新判斷Zp的存在，如果在電壓達到極限的情況下Zp仍然不存在的情況下，應當關停VSG，待清除故障后重新開機。

如果Vpcclt;Vc，表示擾動屬于Ⅱ類大干擾，如果故障不能夠清除，如圖14（b）所示，此時，應當通過提高逆變器的電壓指令來恢復平衡點，在動態增加電壓的過程中時刻檢測Zr的存在。如果在電壓達到極限的情況下Zr仍然不存在的情況下，則需要通過降低功率指令恢復平衡點，使得Zr恢復存在。如果出現過流，則應當調整Zr和降低功率指令值。如果故障可以被清除，如圖 14（c）所示，則應該在每個階段選擇合適的虛擬阻抗。

4 仿真分析

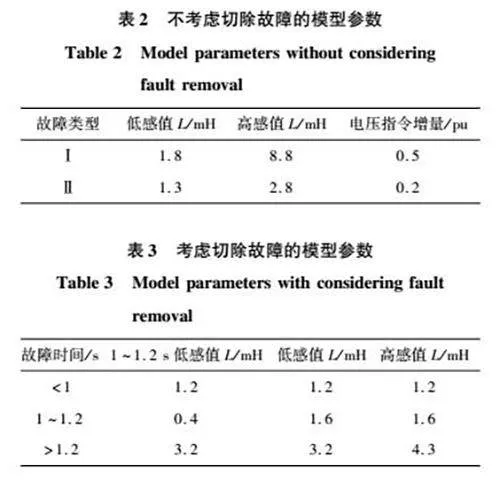
為了驗證本文當中所提的控制策略理論的準確性及可行性，搭建了完整的 VSG 單機無窮大并網系統 Simulink 仿真驗證模型，在仿真模型當中所用到的主要部分參數如表 1 ～ 表 3 所示。"值得說明的是，本文沒有考慮阻抗比對暫態功角穩定性的影響，將阻抗比取了一個定值。

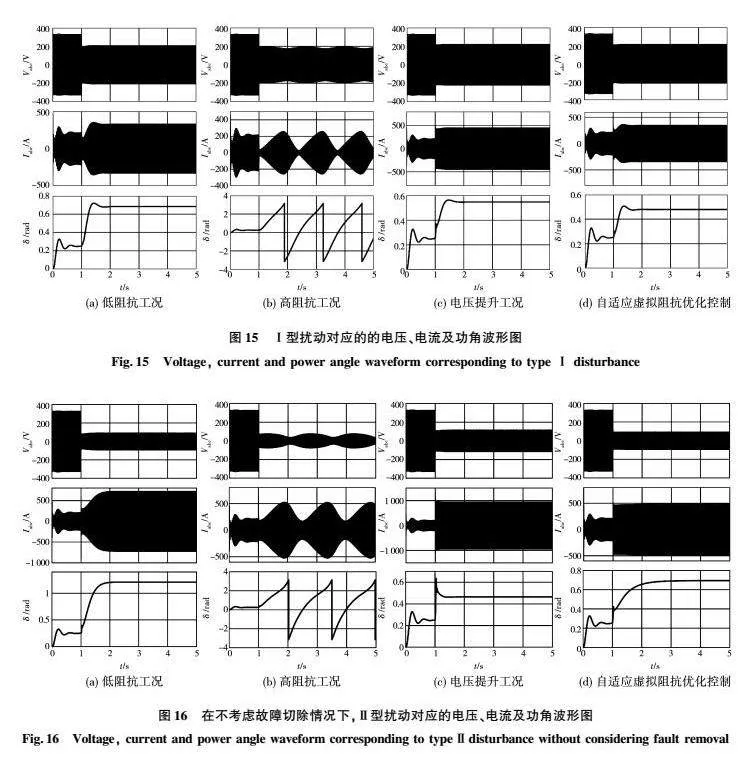
Ⅰ型大擾動對應的仿真結果如圖15所示。其中，圖15（a）顯示的是在沒有Vref作用下，低虛擬阻抗情況下的實驗結果。在t=1 s的時候發生三相短路故障，此時電壓跌落固定值值為04 pu。可以發現，在低虛擬阻抗條件下，功角保持穩定，并且電流峰值滿足15IN的要求。證明了在I型擾動發生后，虛擬阻抗邊界內重疊區域存在。然而，如圖15（b）所示，隨著虛擬阻抗值的增加，功角發生振蕩。在Vref作用下，功角再次穩定，如圖15（c）所示。通過對比圖15（a）和圖15（c）可以發現，Vref雖然使功角穩定，并且此時功角要小于低虛擬阻抗作用下的功角，但是電流卻遠大于低虛擬阻抗作用下的電流。在自適應電壓和虛擬阻抗作用下，情況如圖15（d）所示。通過對比圖15（a）和圖15（d）可以發現，此時兩者電流大小幾乎相同，然而，后者的功角要小于前者。因此，功角穩定性更好。對比圖15（c）和圖15（d），可以發現后者的電流幅值和功角都要好于前者。因此，低虛擬阻抗有利于功角穩定，但不利于限制電流。高虛擬阻抗有利于限制過流，但不利于功角穩定。主動調高電壓指令可以提高功角穩定性，但是會出現過流問題。因此，在主動提高電壓和虛擬阻抗優化的作用下，暫態功角穩定性和過流同時被優化。

對于Ⅱ型大擾動發生情況下，不考慮故障切除條件的仿真結果如圖16所示。其中，圖16（a）展示的是在沒有Vref作用下，低虛擬阻抗情況下的實驗結果。在t=1 s的時候發生三相短路故障，此時電壓跌落值為08 pu。可以發現，在低虛擬阻抗條件下，功角保持穩定，電流峰值大于15IN。證明在Ⅱ型擾動發生后，虛擬阻抗邊界內重疊區域不存在。隨著虛擬阻抗值的增加，電流峰值降低，功角發生振蕩，如圖16（b）所示。在Vref作用下，功角再次穩定，如圖16（c）所示。然而，同樣通過對比圖16（a）和圖16（c）可以發現，Vref雖然使功角穩定，并且此時功角要小于低虛擬阻抗作用下的功角，但是電流卻遠大于低虛擬阻抗作用下的電流。在自適應電壓和虛擬阻抗作用下的情況如圖16（d）所示，通過對比圖16（a）和圖16（d），可以發現此時后者電流峰值小于前者，并且后者的功角也要小于前者。但是，盡管圖16（d）有功參考值降低了50%，然而，VSG的輸出電流仍然無法滿足15IN的要求。因此，一方面可以進一步降低功率指令值，直至滿足電流限制要求，另一方面如果功率區間滿足2IN或更高，那么在故障不切除的情況下，VSG并網系統將保持與電網同步運行。

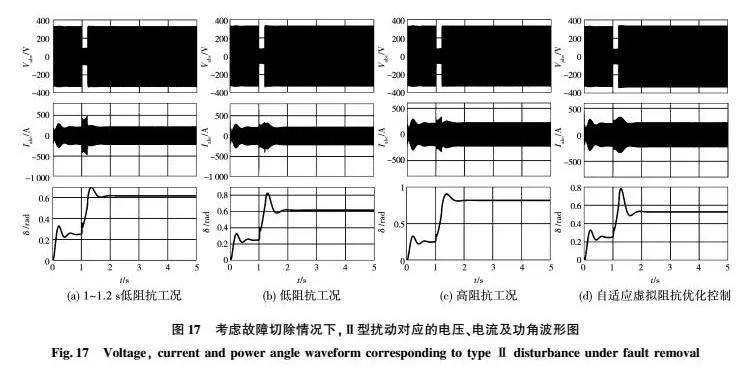
對于Ⅱ型大擾動發生情況下，考慮故障切除條件的仿真結果如圖17所示。對比圖17（a）和圖17（b）可以得知，在1～12 s之間如果虛擬阻抗不滿足Zf的要求，會導致VSG系統出現過電流。對比圖17（b）和圖17（c）可以得知，從雙回線路切換成單回線路之后，由于虛擬阻抗增大，降低了功角的穩定裕度。對比圖17（c）和圖17（d）可以得知，在故障切除后主動提高電壓指令值會提高功角的穩定裕度。

5 結 論

針對不同的運行工況，通過設置電壓增量的自由控制支路可以有效提高暫態功角穩定性，然而，電壓增量的設置需要約束條件。采用本文所提出的基于虛擬阻抗優化的自適應控制算法可以建立約束條件，在保證暫態功角穩定性的前提下，對過電流也可以起到明顯的抑制作用。

通過設置電壓增量的自由控制支路有助于解決在弱電網條件下，虛擬阻抗優化對提高暫態功角穩定性的局限性。因此，無功功率控制環路優化和虛擬阻抗優化對提高暫態功角穩定性可以起到相輔相成的作用。

參 考 文 獻：

［1］"耿華， 何長軍， 劉浴霜，等. 新能源電力系統的暫態同步穩定研究綜述[J]. 高電壓技術， 2022， 48（9）：3367.

GENG Hua， HE Changjun， LIU Yushuang， et al. Overview on transient synchronization stability of renewablerich power systems［J］. High Voltage Engineering， 2022， 48（9）： 3367.

［2］"ZHOU Jenny Z， DING Hui. Impact of short circuit ratio and phase locked loop parameters on the smallsignal behaviour of a VSCHVdc converter[C]//2016 IEEE Power and Energy Society General Meeting （PESGM）， July 17-21， 2016，Boston， MA， USA. 2016： 56.

［3］"HARNEFORS Lennart， BONGIORON Massimo， LUNDBERG Stenfan. Inputadmittance calculation and shaping for controlled voltagesource converters[J]. IEEE Transactions on Industrial Electronics， 2008， 54（6）：3323.

［4］"JIANGHAFNER Ying， MANCHEN Manfred. Stability enhancement and blackout prevention by VSC based HVDC[C]//CIGRE symposium， September 13-15， 2011， Bologna， Italy.2011：42.

［5］"WANG Xiongfei，HARNEFORS Lennart，FREDE Blaabjerg.Unified impedance model of gridconnected voltagesource converters[J].IEEE Transactions on Power Electronics，2018，33（2）：1775.

［6］"FU Xikun， SUN Jianjun， HUANG Meng， et al. Largesignal stability of gridforming and gridfollowing controls in voltage source converter： a comparative study[J].IEEE Transactions on Power Electronics，2021，36（7）：7832.

［7］"WU Heng， WANG Xiongfei. Designoriented transient stability analysis of gridconnected converters with power synchronization control[J]. IEEE Transactions on Industrial Electronics， 2019， 66（8）：6473.

［8］"SHUAI Zhikang， SHEN Chao， YIN Xin， et al. Fault analysis of inverterinterfaced distributed generators with different control schemes[J]. IEEE Transactions on Power Delivery， 2018，33（3）：1223.

［9］"HE Lili， SHUAI Zhikang， ZHANG Xin， et al. Transient characteristics of synchronverters subjected to asymmetric faults[J]. IEEE Transactions on Power Delivery， 2019，34（3）：1171.

［10］"ZHONG Qingchang， WEISS George. Synchronverters： inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics， 2011， 58（4）：1259.

［11］"SHINTAI T， MIURA Y， ISE T.Oscillation damping of a distributed generator using a virtual synchronous generator[J]. IEEE Transactions on Power Delivery， 2014， 29（2）：668.

［12］"SHUAI Zhikang， HUANG Wen， SHEN Zheng John， et al. Active power oscillation and suppression techniques between two parallel synchronverters during load fluctuations[J]. IEEE Transactions on Power Electronics， 2020，35（4）：4127.

［13］"MENG Xin， LIU Jinjun， LIU Zeng.A generalized droop control for gridsupporting inverter based on comparison between traditional droop control and virtual synchronous generator control[J]. IEEE Transactions on Power Electronics， 2019， 34（6）：5416.

［14］"PAQUETTE Andrew D， DIVAN Deepak M.Virtual impedance current limiting for inverters in microgrids with synchronous generators[C]// Energy Conversion Congress and Exposition（ECCE），September 15-19，2013，Denver，CO，USA.2013：1039.

［15］"HUANG Linbin， XIN Huanhai， WANG Zhen， et al. Transient stability analysis and control design of droopcontrolled voltage source converters considering current limitation[J]. IEEE Transactions on Smart Grid， 2019， 10（1）：578.

［16］"LIU Teng， WANG Xiongfei.Transient stability of singleloop voltagemagnitude controlled gridforming converters[J]. IEEE Transactions on Power Electronics， 2021， 36（6）：6158.

［17］"SHUAI Zhikang， SHEN Chao， LIU Xuan， et al. Transient angle stability of virtual synchronous generators using Lyapunov’s direct method[J]. IEEE Transactions on Smart Grid， 2019， 10（4）：4648.

［18］"CHEN M， ZHOU D， BLAABJERG F. Enhanced transient angle stability control of gridforming converter based on virtual synchronous generator[J]. IEEE Transactions on Industrial Electronics， 2021， 69（9）： 9133.

［19］"LI Mingxuan， SHU Sirui， WANG Yue， et al. Analysis and improvement of largedisturbance stability for gridconnected VSG based on output impedance optimization[J]. IEEE Transactions on Power Electronics， 2022（8）：37.

［20］"ZHAO Feng， SHUAI Zhikang， HUANG Wen， et al. A unified model of voltagecontrolled inverter for transient angle stability analysis[J]. IEEE Transactions on Power Delivery， 2021， 37（3）： 2275.

［21］"QORIA T， GRUSON F， COLAS Fréderic， et al. Critical clearing time determination and enhancement of gridforming converters embedding virtual impedance as current limitation algorithm[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2020，8（2）：1050.

［22］"SHUAI Zhikang， SHEN Chao， YIN Xin， et al. Fault analysis of inverterinterfaced distributed generators with different control schemes[J]. IEEE Transactions on Power Delivery， 2018，33（3）：1223.

［23］"張余余， 趙晉斌， 李芬，等. 基于功角動態補償的VSG故障穿越方法研究[J]. 電網技術， 2021，45（9）：3667.

ZHANG Yuyu， ZHAO Jinbin， LI Fen， et al. VSG fault crossing method based on dynamic compensation of power angle［J］. Power System Technology，2021，45（9）： 3667.

［24］"MACHOWSKI J. Power system dynamics—stability and control[M]. New York：Wiley，2008.

［25］"SASAKI H. An approximate incorporation of field flux decay into transient stability analyses of multimachine power systems by the second method of Lyapunov[J]. IEEE Transactions on Power Apparatus and Systems， 1979， 98（2）：473.

［26］"KHALIL H. Nonlinear systems englewood cliffs[M]. NJ， USA：PrenticeHall， 1996.

［27］"葛平娟， 涂春鳴， 肖凡，等. 面向暫態穩定性能提升的VSG參數靈活控制策略[J]. 中國電機工程學報， 2022， 42（6）：2109.

GE Pingjuan， TU Chunming， XIAO Fan， et al. Transient stability enhancement of a VSG based on flexible switching of control parameters［J］. Proceedings of the CSEE， 2022， 42（6）： 2109.

［28］"JIN Zheming， WANG Xiongfei. A DQframe asymmetrical virtual impedance control for enhancing transient stability of gridforming inverters[J]. IEEE Transactions on Power Electronics， 2022， 37（4）： 4535.

［29］"唐英杰， 查曉明， 田震， 等. 弱電網條件下虛擬同步機與SVG并聯系統的暫態穩定性分析[J]. 電網技術， 2022， 46（10）：4020.

TANG Yingjie， ZHA Xiaoming， TIAN Zhen， et al. Transient stability analysis of virtual synchronous generator and SVG parallel system under weak grid conditions［J］. Power System Technology， 2022， 46（10）： 4020.

［30］"XIONG Xiaoling， WU Chao， PAN Donghua， et al. An improved synchronization stability method of virtual synchronous generators based on frequency feedforward on reactive power control loop[J].IEEE Transactions on Power Electronics，2021，36（8）：9136.

［31］"宋丹，張武洋，王成華.含光儲系統的微電網能量協調控制策略［J］.哈爾濱理工大學學報， 2021， 26（6）： 94.

SONG Dan， ZHANG Wuyang， WANG Chenghua. Coordinated control strategy of microgrid energy with optical storage system［J］. Journal of Harbin University of Science and Technology， 2021， 26（6）： 94.

［32］"全少理，樸哲勇，陳鵬浩，等.光伏系統自適應光照和局部遮光的MPPT跟蹤[J].哈爾濱理工大學學報，2020，25（6）：53.

QUAN Shaoli， PIAO Zheyong， CHEN Penghao， et al. MPPT tracking of adaptive lighting and partial shading in photovoltaic systems［J］. Journal of Harbin University of Science and Technology， 2020， 25（6）： 53.

（編輯：劉琳琳）

收稿日期： 2023-04-13

基金項目：國家自然科學基金（U21A20145）；中國博士后科學基金（2021M701018）

作者簡介：孫久亮（1991—），男，博士研究生，研究方向為新能源發電及其并網穩定性控制；

蔡 蔚（1959—），男，博士，教授，博士生導師，研究方向為驅動電機、功率電子控制器及汽車電動化電驅動系統、低振動噪聲電機等；

郭慶波（1987—），男，博士，研究方向為新能源汽車電機驅動器控制、繞組切換、電機優化設計。

通信作者：蔡 蔚