武漢某超高層建筑對(duì)臺(tái)灣花蓮6.9級(jí)地震的結(jié)構(gòu)響應(yīng)分析

羅淵 楊江 范濤

摘要：為研究2022年臺(tái)灣花蓮6.9級(jí)地震對(duì)武漢市某超高層建筑結(jié)構(gòu)的影響，初步分析了該建筑結(jié)構(gòu)4個(gè)加速度測(cè)點(diǎn)記錄的各向PGA放大效應(yīng)、傅立葉譜及反應(yīng)譜，分別利用互功率譜法和基于協(xié)方差的隨機(jī)子空間法分別識(shí)別結(jié)構(gòu)在頻域和時(shí)域上的一階模態(tài)。結(jié)果表明：結(jié)構(gòu)的峰值加速度隨樓層的增高而有顯著的放大效應(yīng)，最大放大倍數(shù)達(dá)7.322倍；各向傅立葉譜峰值均集中在0.275 Hz和1.171 Hz；加速度響應(yīng)反應(yīng)譜遠(yuǎn)小于該地區(qū)Ⅵ度設(shè)防地震設(shè)計(jì)譜；兩種方法識(shí)別的結(jié)構(gòu)一階模態(tài)頻率基本一致，均接近數(shù)值分析值。臺(tái)灣花蓮6.9級(jí)地震沒有對(duì)該高層建筑結(jié)構(gòu)造成損傷。

關(guān)鍵詞：臺(tái)灣花蓮地震；模態(tài)頻率識(shí)別；互功率譜法；隨機(jī)子空間法；結(jié)構(gòu)響應(yīng)觀測(cè)臺(tái)陣

中圖分類號(hào)：TU311.3文獻(xiàn)標(biāo)識(shí)碼：A文章編號(hào)：1000-0666（2024）03-0452-09

doi：10.20015/j.cnki.ISSN1000-0666.2024.0042

0引言

近年來，隨著我國(guó)城市化進(jìn)程的加快，超高層建筑數(shù)量激增。超高層建筑的服役時(shí)間要求長(zhǎng)、耐久性要求高，結(jié)構(gòu)復(fù)雜、高寬比較大，易受外部環(huán)境和荷載（地震、大風(fēng)等）的作用影響。人們根據(jù)震中距場(chǎng)地的遠(yuǎn)近將地震分為近場(chǎng)地震和遠(yuǎn)場(chǎng)地震。有關(guān)震害研究表明，近場(chǎng)地震對(duì)建筑結(jié)構(gòu)的破壞性比遠(yuǎn)場(chǎng)地震嚴(yán)重，因此近場(chǎng)地震研究受到了較為廣泛的關(guān)注（Hall et al，1995；Hall，Aagaard，1998；Zhang，Iwan，2002a，b）。近年來的一些大震災(zāi)害表明，遠(yuǎn)場(chǎng)地震對(duì)建筑結(jié)構(gòu)尤其是超高層建筑結(jié)構(gòu)造成的災(zāi)害同樣不可忽視（杜東升等，2020；張令心，張繼文，2010），其長(zhǎng)周期分量是導(dǎo)致超高層建筑產(chǎn)生結(jié)構(gòu)響應(yīng)的主要原因。超高層建筑結(jié)構(gòu)由于其自振周期較大，在遠(yuǎn)場(chǎng)長(zhǎng)周期地震動(dòng)作用下容易發(fā)生類共振現(xiàn)象而遭到破壞，尤其是大地震產(chǎn)生的長(zhǎng)周期（約2～10 s）地震動(dòng)在大盆地中被放大，會(huì)對(duì)城市高層建筑產(chǎn)生嚴(yán)重威脅（Furumura，Oishi，2023）。如2008年四川汶川8.0級(jí)地震發(fā)生時(shí)，距震中750 km的西安地區(qū)部分高層建筑發(fā)生了較為嚴(yán)重的破壞，距震中3 000 km的泰國(guó)曼谷市中心的一些高樓發(fā)生搖晃，持續(xù)了近7 min（陳平，吳博，2010）。

武漢市位于江漢斷坳與鄂東南褶皺帶的交接地帶，易受遠(yuǎn)場(chǎng)地震的影響，如1986年中國(guó)臺(tái)灣花蓮7.6級(jí)地震、1994年臺(tái)灣海峽7.3級(jí)地震和2008年汶川8.0級(jí)地震發(fā)生時(shí)，武漢市均有震感。2015年，武漢市依據(jù)有關(guān)法律法規(guī)

湖北省人民政府.2006.湖北省地震監(jiān)測(cè)管理實(shí)施辦法.

規(guī)定，高度超過160 m的高層建筑和重大工程設(shè)施均設(shè)置強(qiáng)震動(dòng)監(jiān)測(cè)設(shè)施進(jìn)行結(jié)構(gòu)健康監(jiān)測(cè)，目前武漢市120余棟超高層建筑共布設(shè)了400多個(gè)強(qiáng)震動(dòng)監(jiān)測(cè)點(diǎn)，現(xiàn)已建成全國(guó)最大規(guī)模的監(jiān)測(cè)臺(tái)陣。基于強(qiáng)震動(dòng)監(jiān)測(cè)臺(tái)陣進(jìn)行建筑結(jié)構(gòu)模態(tài)參數(shù)識(shí)別是針對(duì)大型結(jié)構(gòu)的一種有效而實(shí)用的故障診斷和安全檢測(cè)方法，其獲取的結(jié)構(gòu)模態(tài)參數(shù)在結(jié)構(gòu)動(dòng)力特性評(píng)價(jià)、結(jié)構(gòu)振動(dòng)控制（施袁鋒等，2021）、結(jié)構(gòu)損傷診斷與安全性評(píng)價(jià)（何定橋，2021）等領(lǐng)域有重要應(yīng)用。結(jié)構(gòu)模態(tài)識(shí)別常用方法有隨機(jī)子空間識(shí)別法、稀疏時(shí)域法、隨機(jī)減量法、最小二乘法圓擬合、HHT法、正交多項(xiàng)式擬合法、神經(jīng)網(wǎng)絡(luò)模型、小波變換等（張鳴祥等，2022；孫猛猛，2019；秦世強(qiáng)等，2012；單德山，李喬，2015；許斌等，2011；代煜，張建勛，2012；Baker，2007；巴振寧等，2020）。在上述研究的基礎(chǔ)上，何定橋和楊軍（2022）提出了一種基于HHT的結(jié)構(gòu)模態(tài)自動(dòng)識(shí)別方法，利用深度神經(jīng)網(wǎng)絡(luò)和奇異譜分析對(duì)只包含單一模態(tài)信息的固有模態(tài)函數(shù)進(jìn)行模態(tài)參數(shù)識(shí)別；陶冬旺等（2021）利用功率譜法和復(fù)模態(tài)指數(shù)方法對(duì)建筑物結(jié)構(gòu)響應(yīng)記錄的原始數(shù)據(jù)進(jìn)行分析，得到了水平方向前三階的模態(tài)振型和頻率。互功率譜法簡(jiǎn)單易行且算法直觀可信，對(duì)結(jié)構(gòu)的前幾階固有頻率的識(shí)別較為準(zhǔn)確，但該方法在一些真假峰值的辨別上對(duì)人員的經(jīng)驗(yàn)要求較高，在模態(tài)逐漸趨于密集時(shí)該方法存在局限性。隨機(jī)子空間法具有較好的抗噪聲擾動(dòng)能力，適合土木結(jié)構(gòu)尤其是橋梁結(jié)構(gòu)的實(shí)際工程系統(tǒng)識(shí)別問題，能夠比較準(zhǔn)確地識(shí)別結(jié)構(gòu)的模態(tài)參數(shù)，是目前較先進(jìn)的結(jié)構(gòu)環(huán)境振動(dòng)模態(tài)參數(shù)識(shí)別方法。

2022年9月18日中國(guó)臺(tái)灣花蓮縣發(fā)生6.9級(jí)地震，距震中1 000余千米的武漢市某35層超高層建筑結(jié)構(gòu)觀測(cè)臺(tái)陣完整地獲取了這次地震的結(jié)構(gòu)動(dòng)力響應(yīng)。本文以該建筑結(jié)構(gòu)對(duì)花蓮地震的地震動(dòng)響應(yīng)為例，在分析地震動(dòng)響應(yīng)的頻譜、反應(yīng)譜、地震動(dòng)持時(shí)和峰值加速度（PGA）放大效應(yīng)的基礎(chǔ)上，分別采用互功率譜法和基于協(xié)方差的隨機(jī)子空間法兩種方法在頻域和時(shí)域上對(duì)該超高層建筑結(jié)構(gòu)的一階模態(tài)頻率進(jìn)行識(shí)別，并與數(shù)值分析結(jié)果進(jìn)行了對(duì)比分析。

1武漢某超高層建筑臺(tái)陣簡(jiǎn)述

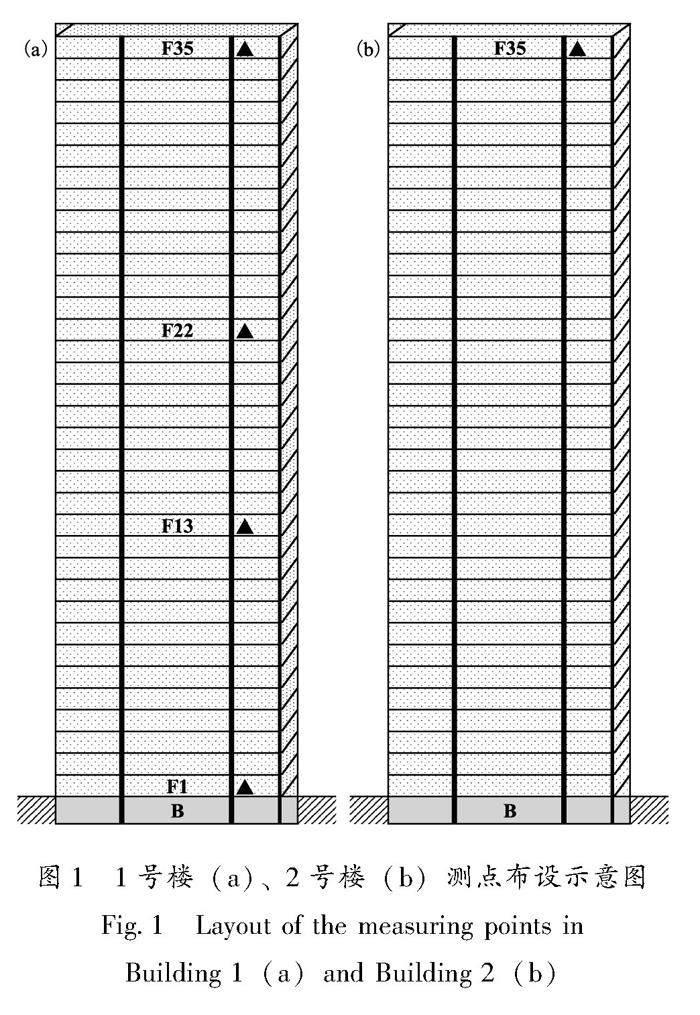
武漢市某超高層建筑強(qiáng)震動(dòng)監(jiān)測(cè)臺(tái)陣布設(shè)于兩棟超高層建筑內(nèi)（下文簡(jiǎn)稱為“1號(hào)樓”和“2號(hào)樓”），兩棟建筑處于相同地塊，相距約50 m，結(jié)構(gòu)布置完全一致，均采用鋼筋混凝土框架剪力墻結(jié)構(gòu)。單棟結(jié)構(gòu)屋面標(biāo)高163.25 m，地下共3層，地上1～2層為小開間單元式商店，1層層高為5.75 m、2層層高為5.4 m，2層連通，3～4層層高4.2 m，5層層高4.35 m，其余辦公樓層高均為4.5 m，在6層、16層、26層設(shè)置避難層，層高為5.95 m。建筑抗震設(shè)防烈度為Ⅵ度，設(shè)計(jì)基本地震加速度值為0.05 g，設(shè)計(jì)地震分組為第一組。分別在1號(hào)樓第1層（標(biāo)高）、第13層（56.85 m）、第22層（98.8 m）、第35層（158.75 m）和2號(hào)樓第35層共布設(shè)5個(gè)三分量一體化力平衡加速計(jì)，結(jié)構(gòu)地震響應(yīng)臺(tái)陣測(cè)點(diǎn)布設(shè)如圖1所示。

2地震動(dòng)數(shù)據(jù)分析

2.1加速度時(shí)程與放大效應(yīng)

在臺(tái)灣花蓮6.9級(jí)地震作用下，結(jié)構(gòu)地震響應(yīng)臺(tái)陣5個(gè)測(cè)點(diǎn)的加速度響應(yīng)時(shí)程曲線如圖2所示，其PGA見表1，對(duì)加速度做2階巴特沃斯帶通濾波（0.01～10 Hz）。從圖中可看出，3個(gè)方向的加速度遠(yuǎn)小于近場(chǎng)地震所引起的地震動(dòng)響應(yīng)，但均符合地震動(dòng)所引起的建筑物樓層振動(dòng)響應(yīng)特性，即加速度的幅值隨樓層的增高而增大。表1顯示，1號(hào)樓和2號(hào)樓頂層的加速度最大，且EW向的加速度最大，分別為4.547和3.842 Gal，其次是NS向。地震動(dòng)在與破裂擴(kuò)展的垂直方向上衰減很快，因此UD向幅值最小。

圖3為根據(jù)5個(gè)測(cè)點(diǎn)的PGA得到的PGA擬合圖，圖中斜率代表放大效應(yīng)，1號(hào)樓各監(jiān)測(cè)點(diǎn)PGA相對(duì)于地面層PGA的比值見表2。從圖3和表2可以看出，EW向PGA隨樓層的增高而快速增大，頂層的PGA為地面層的7.322倍，放大效應(yīng)顯著；NS向和UD向的PGA增長(zhǎng)緩慢，頂層PGA分別為地面層的2.067和2.039倍。

2.2傅立葉譜

圖4為經(jīng)傅立葉變換后得到的各測(cè)點(diǎn)的傅立葉譜。從圖中可以看出，臺(tái)陣各測(cè)點(diǎn)記錄的地震動(dòng)加速度響應(yīng)在0.275 Hz出現(xiàn)一階峰值，且EW向峰值最高，二階峰值集中在1.17 Hz，符合遠(yuǎn)場(chǎng)長(zhǎng)周期地震動(dòng)影響下的結(jié)構(gòu)響應(yīng)特性。在頻域處理信號(hào)時(shí)，通常計(jì)算任一測(cè)點(diǎn)信號(hào)響應(yīng)的傅立葉譜與自功率譜即可得出結(jié)構(gòu)的固有頻率，而傅立葉譜與自功率譜出現(xiàn)最大峰值處對(duì)應(yīng)的頻率即為該結(jié)構(gòu)的一階主頻。根據(jù)1號(hào)樓和2號(hào)樓頂層3個(gè)方向的傅立葉譜分布可以得出，兩棟樓的一階模態(tài)主頻均為0.275 Hz，符合其配置完全相同的設(shè)計(jì)。

2.3反應(yīng)譜

將1號(hào)樓地面層的觀測(cè)加速度近似作為地震動(dòng)輸入，計(jì)算得到結(jié)構(gòu)阻尼比為0.05的加速度反應(yīng)譜及其與Ⅵ度設(shè)防地震設(shè)計(jì)譜的對(duì)比，如圖5所示。從圖中可以看出，距花蓮地震超過1 000 km的武漢某超高層建筑臺(tái)陣，其記錄的加速度響應(yīng)反應(yīng)譜遠(yuǎn)小于Ⅵ度設(shè)防地震設(shè)計(jì)譜。

2.4地震動(dòng)持時(shí)

目前關(guān)于地震動(dòng)持時(shí)的計(jì)算還沒有形成統(tǒng)一的規(guī)范，本文采用相對(duì)一致持時(shí)的規(guī)定值，取相對(duì)于PGA的1/3為起始時(shí)間節(jié)點(diǎn)，到下一次PGA的1/3為終止時(shí)間節(jié)點(diǎn)內(nèi)的連續(xù)時(shí)間段定義為本次地震動(dòng)持續(xù)時(shí)間，5個(gè)測(cè)點(diǎn)的地震動(dòng)持時(shí)見表5。

2.5頂層波形相關(guān)性

從1號(hào)樓和2號(hào)樓頂層的加速度重疊圖（圖6）中可看出，兩棟樓頂層3個(gè)方向的加速度曲線具有較高的吻合度。對(duì)1號(hào)樓和2號(hào)樓頂層NS、EW和UD向的加速度響應(yīng)分別做互相關(guān)可得到2棟樓3個(gè)方向的互相關(guān)系數(shù)分別為0.780、0.795和0.629。可見1號(hào)樓和2號(hào)樓EW向和NS向的加速度響應(yīng)相關(guān)性較高，接近80%，UD向的相關(guān)性較低，結(jié)合圖2分析可能是由于加速度幅度較小，受背景噪聲的影響較大，導(dǎo)致UD向的相關(guān)性較其他兩個(gè)方向偏低。

3一階模態(tài)頻率識(shí)別

結(jié)構(gòu)的一階模態(tài)在荷載激勵(lì)頻率與結(jié)構(gòu)固有頻率相近時(shí)出現(xiàn)，此時(shí)結(jié)構(gòu)的振動(dòng)形態(tài)通常稱為一階振型或主振型。本文主要分析的是在激勵(lì)較小的長(zhǎng)周期地震動(dòng)響應(yīng)下的結(jié)構(gòu)地震動(dòng)響應(yīng)，其一階模態(tài)振型占主導(dǎo)，使用互功率譜法和基于協(xié)方差的隨機(jī)子空間法分別在時(shí)域和頻域上對(duì)結(jié)構(gòu)的一階模態(tài)頻率進(jìn)行識(shí)別，并與數(shù)值分析的結(jié)果進(jìn)行對(duì)比分析。

3.1互功率譜法

互功率譜是模態(tài)參數(shù)識(shí)別中常用的一種方法，由環(huán)境的振動(dòng)響應(yīng)與參考點(diǎn)響應(yīng)中的自功率譜和互功率譜代替頻率響應(yīng)函數(shù)（簡(jiǎn)稱“頻響函數(shù)”），在結(jié)構(gòu)響應(yīng)中，利用結(jié)構(gòu)點(diǎn)響應(yīng)之間的互功率譜與參考點(diǎn)自功率譜的比值來確定模態(tài)的振型和固有頻率。

為了獲得其他結(jié)構(gòu)層地震動(dòng)加速度相對(duì)于結(jié)構(gòu)首層地震動(dòng)加速度的頻響函數(shù)，首先計(jì)算結(jié)構(gòu)首層地震動(dòng)加速度的自相關(guān)函數(shù)，再計(jì)算其他結(jié)構(gòu)層地震動(dòng)加速度分別與結(jié)構(gòu)首層地震動(dòng)加速度的互相關(guān)函數(shù)，最后利用傅立葉變換分別計(jì)算自相關(guān)函數(shù)和互相關(guān)函數(shù)的傅立葉自功率譜和互功率譜，通過下式構(gòu)建頻響函數(shù)Hn1（f）表示為：

Hn1（f）=Pa1an（f）Pa1a1（f）（1）

式中：Pa1an（f）為根據(jù)第n結(jié)構(gòu)層地震動(dòng)加速度an與結(jié)構(gòu)首層地震動(dòng)加速度a1構(gòu)建的互相關(guān)函數(shù)求得的互功率譜；Pa1a1（f）為根據(jù)結(jié)果首層地震動(dòng)加速度構(gòu)建的自相關(guān)函數(shù)求得的自功率譜。

花蓮6.9級(jí)地震引起的1號(hào)樓結(jié)構(gòu)樓層水平方向的頻響函數(shù)如圖7所示。從圖中可以看出一階特征峰值十分突出，13層、22層和35層EW向的頻響函數(shù)的峰值頻率均為0.291 Hz，NS向?yàn)?.275 Hz。

3.2基于協(xié)方差的隨機(jī)子空間法

隨機(jī)子空間方法可分為基于協(xié)方差驅(qū)動(dòng)隨機(jī)子空間識(shí)別法（Cov-SSI）和基于數(shù)據(jù)驅(qū)動(dòng)隨機(jī)子空間識(shí)別法（Data-SSI），其基本原理都是以線性系統(tǒng)的最小實(shí)現(xiàn)理論為基礎(chǔ)，利用Hankel 矩陣與系統(tǒng)可觀測(cè)性、可控制性矩陣的特殊關(guān)系求得系統(tǒng)矩陣A和輸出矩陣C，在狀態(tài)空間辨識(shí)系統(tǒng)的模態(tài)參數(shù)。

本文利用Cov-SSI法，首先根據(jù)地震動(dòng)響應(yīng)數(shù)據(jù)構(gòu)建Hankel矩陣，通過計(jì)算獲得的協(xié)方差序列組成Toeplitz矩陣，經(jīng)過奇異值分解（Sigular Value Decomposition，SVD）求出系統(tǒng)矩陣，從而得到結(jié)構(gòu)的模態(tài)參數(shù)。通常Hankel矩陣劃分為兩塊，第一塊稱作“過去輸出”，第二塊稱作“未來輸出”，可表示為：

H0，2i-1=1[KF（]j[KF）][JB（（][HL（4]y0y1…yj-1[XZ（135#][XZ）]yi-1yi…yi+j-2yiyi+1…yi+j-1[XZ（135#][XZ）]y2i-1y2i…y2i+j-2[HL）][JB））][KH*2D]=（H0，i-1Hi，2j-1）=（[SX（]HpastHfuture[SX）]）（2）

式中：Hankel矩陣是由2i行、j列組成的矩陣；yi為系統(tǒng)的輸出，因?yàn)殡S機(jī)系統(tǒng)需要足夠量的統(tǒng)計(jì)分析，所以假定j→∞；H0，2i-1下標(biāo)的0表示Hankel矩陣第1列第1個(gè)元素的下標(biāo)，2i-1表示第1列最后一個(gè)元素的下標(biāo)，矩陣行數(shù)取決于輸出數(shù)據(jù)響應(yīng)的通道數(shù)和系統(tǒng)最大計(jì)算階數(shù)。

由于Cov-SSI法采用的是隨機(jī)狀態(tài)空間模型，其協(xié)方差輸出表示為：

Λi=[SX（]1j[SX）]∑[DD（]j-1k=0[DD）]hk+1hTk（3）

由一系列協(xié)方差矩陣組成的Toeplitz矩陣可寫為：

T1/i=YfYTP=[JB（（][HL（5]ΛiΛi-1Λi-2…Λ1Λi+1ΛiΛi-1…Λ2Λi+2Λi+1Λi…Λ3[XZ（135#][XZ）]Λ2i-1Λ2i-2Λ2i-3…Λi[HL）][JB））]（4）

對(duì)式（4）進(jìn)行SVD分解求得系統(tǒng)狀態(tài)矩陣和輸出矩陣，并對(duì)狀態(tài)矩陣進(jìn)行特征值分解得到包含復(fù)特征值的對(duì)角矩陣和特征向量組成的矩陣，最后求得結(jié)構(gòu)模態(tài)頻率等模態(tài)參數(shù)。

本文分別對(duì)1號(hào)樓的EW向和NS向兩個(gè)水平分量分別做Cov-SSI識(shí)別，計(jì)算出的模態(tài)穩(wěn)定圖如圖7中星點(diǎn)圖所示，根據(jù)圖中頻率、阻尼和模態(tài)穩(wěn)定點(diǎn)可識(shí)別出一階模態(tài)頻率分別為0.276和0.294 Hz。

3.3一階模態(tài)頻率對(duì)比

表4給出了一階模態(tài)頻率的數(shù)值分析值以及互功率譜法和Cov-SSI法計(jì)算得出的計(jì)算值。其中，數(shù)值分析值來源于該高層建筑的超限高層建筑工程抗震設(shè)防可行性論證報(bào)告，采用了盈建科建筑結(jié)構(gòu)設(shè)計(jì)軟件YJK-EP模塊對(duì)結(jié)構(gòu)進(jìn)行動(dòng)力彈塑性時(shí)程分析，基于YJK彈性分析，得到根據(jù)構(gòu)件配筋數(shù)據(jù)形成構(gòu)件截面的彈塑性分析參數(shù)。

從圖7可以看出，識(shí)別結(jié)果有較好的一致性。從表4可見，使用互功率譜法和Cov-SSI法得到的EW向和NS向的一階模態(tài)頻率差值分別為0.015和0.023 Hz，相對(duì)誤差分別為5.4%和7.7%，且兩種方法的計(jì)算值與傅立葉頻譜識(shí)別值0.275 Hz較為接近，這與兩棟建筑結(jié)構(gòu)實(shí)際布置一致。如果以數(shù)值分析值為真實(shí)值，兩種方法得到的EW向的一階模態(tài)頻率與數(shù)值分析值分別相差0.077和0.062 Hz，相對(duì)誤差分別為36%和29%。NS向的一階模態(tài)頻率與數(shù)值分析值分別相差0.042和0.065 Hz，相對(duì)誤差分別為18%和28%。

4結(jié)論

本文對(duì)布設(shè)在武漢某超高層建筑強(qiáng)震動(dòng)監(jiān)測(cè)臺(tái)陣獲取的臺(tái)灣花蓮6.9級(jí)地震動(dòng)響應(yīng)進(jìn)行了傅立葉峰值、地震動(dòng)持時(shí)、PGA放大效應(yīng)及其與結(jié)構(gòu)頂層的相關(guān)性分析；分別利用互功率譜法和基于協(xié)方差的隨機(jī)子空間法分別在頻域和時(shí)域上對(duì)1號(hào)樓的一階模態(tài)進(jìn)行識(shí)別，并與傅立葉譜幅值特性確定的一階頻率進(jìn)行對(duì)比，主要得到以下結(jié)論：

（1）各測(cè)點(diǎn)所在樓層地震動(dòng)持續(xù)時(shí)間均有所不同；隨著樓層的增高，水平向和縱向的PGA均存在放大效應(yīng)，EW向的PGA放大效應(yīng)最明顯，頂層的PGA放大效應(yīng)最顯著，約為地面層的7.322倍，NS向和UD的PGA分別為地面層的2.067倍和2.039倍；各測(cè)點(diǎn)3個(gè)方向的傅立葉譜峰值均集中在0.275和1.171 Hz；結(jié)構(gòu)反應(yīng)能量主要以第一階頻率0.275 Hz為主，接近結(jié)構(gòu)一階模態(tài)頻率識(shí)別結(jié)果；兩棟樓頂層EW向和NS向的加速度響應(yīng)相關(guān)性較高，而UD向加速度響應(yīng)可能受背景噪聲的影響，相關(guān)性不高；結(jié)構(gòu)地面層的3個(gè)方向反應(yīng)譜峰值遠(yuǎn)小于設(shè)計(jì)反應(yīng)譜，分析認(rèn)為臺(tái)灣花蓮6.9級(jí)地震沒有對(duì)該高層建筑結(jié)構(gòu)造成損傷。

（2）采用互功率譜法和基于協(xié)方差的隨機(jī)子空間法得到1號(hào)樓EW向和NS向的一階模態(tài)頻率相對(duì)誤差分別為5.4%和7.7%，并且這兩種方法計(jì)算值均略大于數(shù)值分析值，EW向相對(duì)誤差分別為36%和29%，NS向相對(duì)誤差分別為18%和28%。這可能與填充墻對(duì)結(jié)構(gòu)剛度的影響有關(guān)，填充墻自身結(jié)構(gòu)的質(zhì)量和荷載對(duì)結(jié)構(gòu)的剛度有一定提升作用，而數(shù)值分析建模未考慮填充墻對(duì)結(jié)構(gòu)剛度的影響。綜上分析認(rèn)為，臺(tái)灣花蓮6.9級(jí)地震對(duì)武漢某超高層建筑結(jié)構(gòu)沒有造成損壞。

參考文獻(xiàn)：

巴振寧，焦鵬，劉冰松，等.2020.嘉峪關(guān)光化樓磚墻結(jié)構(gòu)對(duì)抗震性能的影響［J］.地震研究，43（3）：500-507.Ba Z N，Jiao P，Liu B S，et al.2020.The influence of brick wall structure of Jiayuguan Guanghua building on seismic performance［J］.Journal of Seismological Research，43（3）：500-507.（in Chinese）

陳平，吳博.2010.汶川地震中西安高層建筑震害調(diào)查及分析［J］.水利與建筑工程學(xué)報(bào)，8（2）：60-62.Chen P，Wu B.2010.Seismic damage investigation and analysis for high structure of Xian in Wenchuan Earthquake［J］.Journal of Water Resources and Architectural Engineering，8（2）：60-62.（in Chinese）

代煜，張建勛.2012.基于小波變換和反向傳播網(wǎng)絡(luò)的模態(tài)參數(shù)辨識(shí)［J］.振動(dòng)與沖擊，31（3）：55-59.Dai Y，Zhang J X.2012.Identification of modal parameters based on wavelet transform and back propagation network［J］.Journal of Vibration and Shock，31（3）：55-59.（in Chinese）

杜東升，宋寶璽，許偉志，等.2020.高層鋼結(jié)構(gòu)考慮長(zhǎng)周期地震動(dòng)的減震加固研究［J］.工程力學(xué)，37（7）：189-200.Du D S，Song B X，Xu W Z，et al.2020.Seismic retrofit of a high-rise steel structure considering long-period and long-duration ground motions［J］.Mechanics，37（7）：189-200.（in Chinese）

何定橋，楊軍.2022.基于HHT的結(jié)構(gòu)模態(tài)參數(shù)自動(dòng)化識(shí)別方法和試驗(yàn)驗(yàn)證［J］.工程力學(xué)，39（11）：109-122.He D Q，Yang J.2022.An automatic structural modal parameters identification method based on HHT and its experimental verification［J］.Engineering Mechanics，39（11）：109-122.（in Chinese）

何定橋.2021.建筑結(jié)構(gòu)地震響應(yīng)監(jiān)測(cè)和風(fēng)險(xiǎn)評(píng)估算法研究［D］.北京：清華大學(xué).He D Q.2021.Structural seismic response monitoring and risk assessment algorithm study［D］.Beijing：Tsinghua University.（in Chinese）

秦世強(qiáng)，蒲黔輝，施洲.2012.環(huán)境激勵(lì)下大型橋梁模態(tài)參數(shù)識(shí)別的一種方法［J］.振動(dòng)與沖擊，31（2）：95-100.Qin S Q，Pu Q H，Shi Z.2012.A method of modal parameters identification using ambient vibration measurements for a large-scale bridge［J］.Journal of Vibration and Shock，31（2）：95-100.（in Chinese）

單德山，李喬.2015.橋梁結(jié)構(gòu)模態(tài)參數(shù)的時(shí)頻域識(shí)別［J］.橋梁建設(shè)，31（2）：26-31.Shan D S，Li Q.2015.Model parameters of bridge structure in time-frequency domain［J］.Bridge Construction，31（2）：26-31.（in Chinese）

施袁鋒，朱正言，陳鵬，等.2021.基于EM算法和模態(tài)形式的狀態(tài)空間模型自降階工作模態(tài)分析［J］.工程力學(xué)，38（9）：15-25.Shi Y F，Zhu Z Y，Chen P，et al.2021.Operational modal analysis using EM algorithm and modal-form state-space model with auto model order reduction［J］.Engineering Mechanics，38（9）：15-25.（in Chinese）

孫猛猛.2019.非平穩(wěn)環(huán)境激勵(lì)下高層建筑結(jié)構(gòu)模態(tài)參數(shù)識(shí)別［D］.武漢：武漢理工大學(xué).Sun M M.2019.Modal parameter identification of high-rise building under non-stationary environmental excitation［D］.Wuhan：Wuhan University of Technology.（in Chinese）

陶冬旺，劉泉，馬強(qiáng)，等.2021.云南漾濞地震大理某高層建筑結(jié)構(gòu)地震響應(yīng)觀測(cè)數(shù)據(jù)初步分析［J］.世界地震工程，37（3）：19-30.Tao D W，Liu Q，Ma Q，et al.2021.Preliminary analysis of structural seismic response of a tall building in Dali recorded in Yunnan Yangbi earthquakes［J］.World Earthquake Engineering，37（3）：19-30.（in Chinese）

許斌，龔安蘇，賀佳，等.2011.基于神經(jīng)網(wǎng)絡(luò)模型的結(jié)構(gòu)參數(shù)提取新方法［J］.工程力學(xué)，28（4）：35-41.Xu B，Gong A S，He J，et al.2011.A novel structural parameter extraction with neural network based nonparametric model［J］.Engineering Mechanics，28（4）：35-41.（in Chinese）

張令心，張繼文.2010.近遠(yuǎn)場(chǎng)地震動(dòng)及其地震影響分析［J］.土木建筑與環(huán)境工程，32（2）：84-86.Zhang L X，Zhang J W.2010.Analysis of near far field vibration and its seismic effects［J］.Journal of Civil & Environmental Engineering，32（2）：84-86.（in Chinese）

張鳴祥，廖海飛，王建國(guó)，等.2022.大跨度橋梁顫振時(shí)域的直接分析法［J］.合肥工業(yè)大學(xué)學(xué)報(bào)（自然科學(xué)版），45（4）：487-492.Zhang M X，Liao H F，Wang J G，et al.2022.Time domain flutter direct analysis of long-span bridges［J］.Journal of Hefei University of Technology（Natural Science），45（4）：487-492.（in Chinese）

Baker J W.2007.Quantitative classification of near-fault ground motions using wavelet analysis［J］.Buletin of the Seismological Society of America，97（5）：1486-1501.

Furumura T，Oishi Y.2023.An early forecast of long-period ground motions of large earthquakes based on deep learning［J］.Geophysical Research Letters，50（6）：1-9.

Hall J F，Aagaard B T.1998.Fundamentals of the near-source problem［C］//Proceedings of the 5th Caltrans Seismic Research Workshop Sacramento，10.

Hall J F，Heaton T H，Hailing M W，et al.1995.Near-source ground motion and its effects on flexible buildings［J］.Earthquake Spectra，l1（4）：569-605.

Zhang Y，Iwan W D.2002a.Active interaction control of tall buildings subjected to near-field ground motions［J］.Journal of Structural Engineering，128（1）：69-79.

Zhang Y，Iwan W D.2002b.Protecting base-isolated structures from near-field ground motion by tuned interaction damper［J］.Journal of Engineering Mechanics，128（3）：287-295.

Analysis of the Structural Response of a Super High-rise Building in Wuhan?to the Hualian，Taiwan MS6.9 Earthquake

LUO Yuan1，YANG Jiang1，2，3，F(xiàn)AN Tao1，2，3

（1.Institute of Seismology，China Earthquake Administration，Wuhan 430071，Hubei，China）

（2.Wuhan Institute of Seismic Scientific Instruments Co.Ltd.，Wuhan 430071，Hubei，China）

（3.Engineering Technology Research Center for Earthquake Monitoring and Early Warning Disposal?of Major Projects in Hubei Province，Xianning 437000，Hubei，China）

Abstract

Wuhan city is located at the junction of the Jianghan Fault Depression and the Southeastern Hubei Fold Belt，which is often affected by far-field earthquakes.At 14：00 on September 18，2022，a 6.9-magnitude earthquake occurred in Hualian County，Taiwan Province of China.The structural dynamic response of a super high-rise building to the Hualian earthquake was completely recorded at 4 monitoring points in this building in Wuhan，more than 1000 km away from the epicenter.In order to study the impact of the earthquake on the building structure，the anisotropic PGA amplification effect，the Fourier spectrum and the response spectrum are analyzed.The mutual power spectrum method and the stochastic subspace identification method based on covariance are used respectively to identify the first-order modes of the structure in the frequency domain and the time domain.The results show that the peak acceleration of the structure has a significant amplification effect with the increase of the height of the floor，and the maximum amplification factor is 7.322.The peak value of the Fourier spectrum is concentrated at 0.275 Hz and 1.171 Hz.The response spectrum of acceleration response is much smaller than the design spectrum of the Ⅵ-degree fortification earthquake in this area.The frequencies of the firstorder modes identified by the two methods are generally the same，and are close to the values of numerical simulation.It is believed that the Hualian，Taiwan MS6.9 earthquake did not cause damage to the structure of the case building.

Keywords：?the Hualian，Taiwan earthquake；modal frequency identification；the mutual power spectrum method；the stochastic sub-space method；the structural response observation array

*收稿日期：2023-07-24.

基金項(xiàng)目：中國(guó)地震局地震研究所和應(yīng)急管理部國(guó)家自然災(zāi)害防治研究院基本科研業(yè)務(wù)費(fèi)專項(xiàng)資助項(xiàng)目（IS202216317）；湖北省重點(diǎn)研發(fā)計(jì)劃項(xiàng)目（2022BAD059）；地震科技星火計(jì)劃項(xiàng)目（XH23027YB）.

第一作者簡(jiǎn)介：羅淵（1997-），碩士研究生在讀，主要從事防災(zāi)減災(zāi)技術(shù)研究.E-mail：1070732111@qq.com.

通信作者簡(jiǎn)介：楊江（1980-），高級(jí)工程師，主要從事觀測(cè)技術(shù)研究.E-mail：meblor@whsii.com.

羅淵，楊江，范濤.2024.武漢某超高層建筑對(duì)臺(tái)灣花蓮6.9級(jí)地震的結(jié)構(gòu)響應(yīng)分析［J］.地震研究，47（3）：452-460，doi：10.20015/j.cnki.ISSN1000-0666.2024.0042.

Luo Y，Yang J，F(xiàn)an T.2024.Analysis of the structural response of a super high-rise building in Wuhan to the Hualian， Taiwan MS6.9 earthquake ［J］.Journal of Seismological Research，47（3）：452-460，doi：10.20015/j.cnki.ISSN1000-0666.2024.0042.