相對論體系下衛星原時及星間鐘差機理建模

賈前，李青，劉磊

（1.西北工業大學航天學院，西安 710072；2.陜西省空天飛行器設計重點實驗室，西安 710072；3.清華大學航天航空學院，北京 100084）

0 引言

星載原子鐘是衛星導航系統的核心部件，其性能決定了導航系統時間基準的精度［1-2］。目前，地面光學原子鐘的穩定度即將突破10-19量級［3-4］，JPL 的星載汞離子鐘已通過在軌驗證，比目前應用的星載原子鐘精度提高了1 個量級以上，有望應用于新一代衛星導航系統［5］。然而，空間中變化的引力場以及衛星的運動會導致星載原子鐘計量的原時產生偏差［6］，不同衛星的原時偏差導致了星間鐘差，影響對原子鐘性能極限的利用［7］。新一代導航衛星均計劃或已經通過確定星間鐘差來建立與維持星座自主時間基準［8］，以實現導航系統的自主運行，但衛星原時及星間皮秒鐘差機理尚不清晰。為滿足新一代導航系統對高精度自主時間基準的需求，亟需開展衛星原時偏差以及星間皮秒鐘差模型研究。

在衛星原時偏差方面，國內外學者基于衛星鐘的物理模型以及相對論效應研究了多種模型。基于衛星鐘的物理模型主要利用原子鐘的數據進行模型參數求解，進而得到鐘差數據，精度在ns 量級［9］。常用的模型有多項式模型［10］、灰色模型［11］、譜分析模型［12］、時間序列模型［13］以及組合模型［14］等。文獻［15］提出了二次多項式擬合預報模型，基于衛星鐘的物理特性擬合得到衛星鐘差，文獻［9］在二次多項式模型基礎上增加了顯著周期項，并結合BP神經網絡設計了超快速鐘差預報算法實現流程。然而上述模型需要衛星的精密鐘差數據與原子鐘的隨機先驗信息，且精度無法滿足新一代導航系統分米級導航定位需求［9］。基于相對論效應的模型通過研究衛星原時速率與引力場及衛星運動的關系得到衛星原時偏差。文獻［6］與文獻［16］在開普勒軌道假設下研究了GPS 和北斗衛星導航系統（BDS）衛星原子鐘的相對論效應，并指出周期性累積鐘差需要根據衛星星歷實時進行計算和改正，但未考慮攝動對星載原子鐘的影響。文獻［17］以地球同步軌道衛星為研究對象分析了軌道攝動引起的鐘差，文獻［18］估計了地球J2 項攝動引起Galileo 衛星的原時偏差幅值，文獻［19］建立了衛星原時與坐標時轉換模型，并指出J2 項攝動引起的原時偏差對于中軌道衛星達到了納秒量級。根據文獻［6］和文獻［16-19］的研究可知，基于廣義相對論的鐘差模型可實現的精度更高，但仍需要在開普勒軌道假設的基礎上引入J2 項修正以達到皮秒級精度。星間鐘差主要基于星間鏈路獲得的觀測數據進行計算，目前雙向測量工作體制的星間鏈路已經用于高精度的鐘差測量［20］。文獻［21］提出了一種利用星間偽距擬合多項式和鐘差擬合多項式聯合求解星間鐘差算法，精度在5ns 以內。文獻［22］針對北斗2 導航系統的星間鏈路建立了同步時分雙工（STDD）體制下星間鐘差測量模型，精度優于1ns；文獻［23］研究了STDD體制下星間鐘差的測量誤差模型，并與GPS 采用的輪詢時分雙工體制（PTDD）進行了對比，驗證了其性能。文獻［21-23］所采用的方法主要以激光或者微波為信號載體，通過計算兩終端發射接收信號的時間差來確定鐘差，精度取決于不同路徑中延時修正模型，且未從原時模型角度研究星間皮秒鐘差機理。文獻［19］在開普勒軌道的假設下利用衛星原時模型建立了星間鐘差模型，能夠有效計算星間鐘差，但該模型并未考慮攝動加速度，誤差會隨時間增加而增大。

本文從廣義相對論出發，提出一種考慮J2 項攝動的衛星原時和星間鐘差模型，根據衛星的位置速度信息計算得到衛星原時偏差以及星間鐘差，并通過仿真對模型進行驗證，為星載原子鐘的校正和星間鐘差確定提供了一種可行的建模方法。

1 坐標系與衛星運動方程

1.1 坐標系描述

為建立衛星運動與時間的聯系，首先借助廣義相對論建立衛星的運動方程。運動的描述離不開相應的坐標系，本文選擇地心參考坐標系（Geocentric coordinate reference system，GCRS）建立地球引力場中衛星的運動模型。GCRS的原點在地球質量中心，并且由四維坐標X≡(ct，x，y，z)T所定義，其中c為真空中的光速，值為2.997 924 58×108m/s，t為坐標系對應的坐標時，x，y，z為衛星的空間位置坐標。在GCRS中，兩個確定事件的間隔微分ds可以表示為：

式中：gμυ為GCRS 的度規張量；xμ，υ(μ，υ=0，1，2，3)為GCRS中的時空坐標分量，μ，υ=0時，x0=ct，μ，υ=1，2，3分別對應衛星的三軸坐標分量x，y，z。

度規張量可以由一組諧波勢表示，諧波勢包含標量勢w與矢量勢wE，保留至c-4項，選取度規張量為［24］：

式中：α，β和λ為索引標號，從1取至3；γ=diag(-1，-1，-1) ;為wE的第λ個分量。

矢量勢wE的表達式為：

式中：G為引力常數，值為6.673 5×10-11N·m2/kg2；ME為地球的質量，為5.974 2×1024kg；r=‖r‖2為衛星地心距；r=[x，y，z]T為衛星在GCRS 中的位置矢量；SE=[0，0，9.8 × 108]Tm2s為地球單位質量的角動量；“(·)×”符號表示矢量叉乘運算的反對稱矩陣：

地球引力場中，標量勢w由地球引起的引力勢UE和其他天體引起的潮汐勢組成，表達式為：

考慮地球引力勢至J4項，UE的表達式為：

式中：RE為地球平均赤道半徑，取值為6 378 km；J2，J3和J4為地球的二至四階帶諧系數，值分別為1.082 6×10-3，-2.532 7×10-6和-1.619 6×10-6；為簡化描述，定義UJ為地球的二至四階帶諧項引起的引力勢變化的總和。

式中：Mb為天體b 的質量，太陽質量MS為1.980 4×1030kg，月球質量MM為7.336 9×1022kg；rbE為天體b與地球之間的距離；nbE=rbErbE為rbE的單位向量；符號S和M分別代表太陽和月球。

1.2 衛星運動方程

考慮衛星運動的相對論效應時，可以在牛頓體系下衛星的運動方程中添加相應的相對論修正項，也可以利用度規張量直接在廣義相對論體系下建立衛星的運動學方程，本文選擇第2種方式。

根據式（1）以及選擇的度規張量，可以得到兩事件的時空間隔微分為：

衛星的運動方程以坐標時t為變量，因此引入拉格朗日乘子L=dsdt，根據式（8）可得拉格朗日乘子的平方表達式為：

式中：v=為衛星運動速度大小；vx=dxdt，vy=dydt，vz=dzdt分別為衛星各軸向的速度大小。

對式（9）進行開方并保留至c-4項，可得拉格朗日乘子L的表達式為：

拉格朗日乘子L應滿足Euler-Lagrange方程：

將式（10）代入式（11），并引入非引力項以及日地相對運動引起的加速度項［24］，推導可得廣義相對論體系下衛星的運動方程為：

式中：n=r r為衛星位置r的單位向量；rSE為太陽相對地球的位置向量，且為非引力項產生的衛星加速度。

2 考慮J2項修正的衛星原時以及星間鐘差模型

2.1 衛星原時模型

衛星在軌運行時，星載原子鐘記錄的時間稱為原時τ，原時速率會受到衛星運動與引力場的影響發生改變，而坐標時僅與選定的坐標系相關［16］，因此可通過建立坐標時與原時的關系得到衛星的原時模型。在衛星附近的無窮小區域內，度規張量為常值，且原子鐘相對衛星靜止，即dx=dy=dz=0，因此可得：

聯立式（8）與（13）可得衛星原時模型為：

式中：δ(r，v)為由于衛星運動與引力勢的存在而產生的原時速率偏差。假設坐標時為導航系統的參考時間，此時原時偏差即為對應的衛星鐘差，如圖1所示。

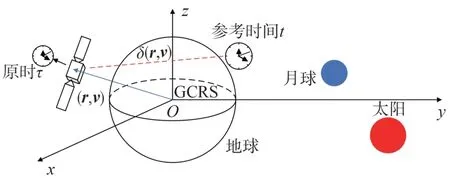
圖1 引力場中原時偏差示意圖Fig.1 Schematic of proper time deviation in the gravitational field

僅考慮地球引力勢中的牛頓主項，忽略其他天體引起的潮汐勢，即標量勢w簡化為：

在地球引力場內，衛星所在位置處的引力勢主要為地球產生的影響，并且J2 項的量級遠大于高階項，因此在引力勢中引入地球非球形J2 項攝動，得到考慮J2項修正的衛星原時模型為：

衛星的狀態也可以通過軌道六要素來表示，將式（17）中對應的變量轉換為軌道六要素，即可得到基于軌道六要素的衛星原時模型。

衛星地心距r的表達式為：

式中：a為衛星所在軌道的半長軸；e為軌道偏心率；E為偏近點角。

衛星的z軸位置分量可表示為：

式中：i為軌道傾角；f為真近點角；ω為近地點幅角。

衛星的地心距與速度大小滿足：

聯立式（18）和（20）可得：

在軌道偏心率較小的情況下，根據軌道攝動理論，考慮J2項攝動，相關軌道參數可以表示為：

式中：a0，i0，e0，ω0和E0分別為不受攝動影響的衛星軌道對應的半長軸，軌道傾角，偏心率，近地點幅角以及偏近點角。

將式（18），（19），（21）以及式（22）聯立，忽略高階小量，代入式（17）可得到基于軌道六要素的衛星原時模型為：

根據式（23）可以看到，衛星運行過程中原時與坐標時產生的差異由四部分組成，前兩項表示僅考慮牛頓主項加速度時衛星在軌運動引起的相對論效應，后兩項為J2項攝動引起的相對論效應。

2.2 星間鐘差模型

根據式（17）可以看到，當衛星的狀態不同時，衛星原時相對參考時間的差異不同。而導航系統通常由多顆衛星組成，這些衛星分布在不同軌道面或者同一軌道面的不同位置處，因此導航衛星的狀態間存在差異，在軌運行時不同的衛星原時會產生對應的星間鐘差，如圖2所示。

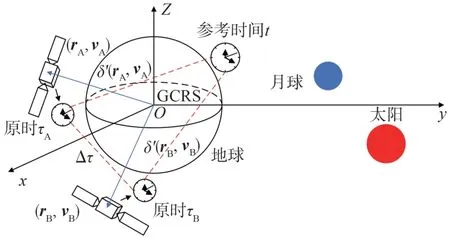
圖2 星間鐘差示意圖Fig.2 Schematic of inter-satellite clock difference

考慮導航系統中兩顆衛星A和B，假設在坐標時t0時刻，兩顆衛星的星載原子鐘讀數即原時分別為τA0和τB0，初始鐘差為Δτ0=τB0-τA0，則在t1時刻兩顆衛星的原時可以表示為：

進一步對兩顆衛星的原時作差，可以得到衛星A和B的星間鐘差為：

式（25）即為考慮J2 項修正的星間鐘差模型，該模型分為四部分：（1）衛星初始鐘差；（2）衛星地心距差異引起的星間鐘差；（3）衛星速度差異引起的星間鐘差；（4）J2項攝動引起的星間鐘差。

3 仿真分析

3.1 衛星軌道誤差仿真

北斗衛星導航系統（BDS）是我國自主建立的全球衛星導航系統，可在全球范圍內全天候、全天時為各類用戶提供高精度、高可靠定位、導航、授時服務。本節以BDS 中北斗三號MEO-01 衛星為研究對象，對建立的衛星運動方程進行仿真分析，非引力項加速度考慮為太陽光壓引起的加速度，計算方式參考文獻［19］。仿真中衛星的初始軌道要素如表1所示，仿真時長為兩個軌道周期，仿真步長為1 s，仿真時為坐標時。

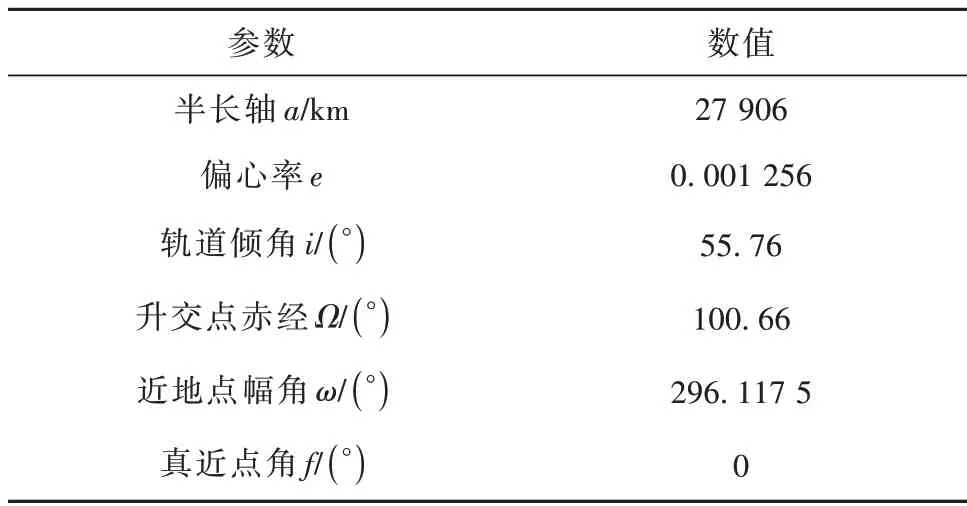
表1 北斗三號-MEO-01衛星初始軌道要素Table 1 Initial orbital elements of BeiDou-3 MEO-01 satellite

考慮式（12）右端的全部加速度項時，攝動加速度引起的衛星位置誤差以及速度誤差分別如圖3和圖4 所示，兩者均隨時間的增加而增大。對于MEO-01 衛星而言，在兩個軌道周期時，位置誤差已經達到了25.48 km，速度誤差達到了3.78 m/s，根據衛星原時模型可知，這些誤差均會導致原時與坐標時之間產生偏差。

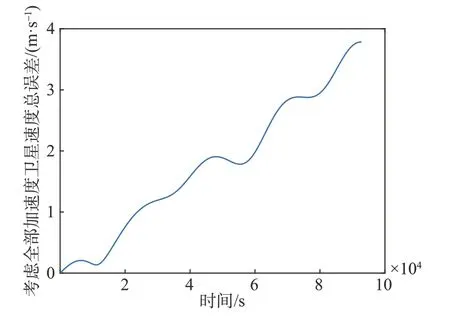
圖4 攝動加速度引起的速度總誤差Fig.4 Total velocity error induced by perturbation acceleration

僅考慮J2 項攝動加速度時，MEO-01 衛星的位置誤差以及速度誤差如圖5 和圖6 所示。根據仿真結果可知，J2 項攝動加速度引起的位置誤差與速度誤差與模型考慮的全部攝動加速度引起的誤差變化趨勢相同。兩個軌道周期時，J2 項攝動加速度引起的位置誤差為21.11 km，速度誤差為3.22 m/s。與圖3和圖4仿真結果對比可知，在考慮的攝動加速度中，J2 項攝動加速度對MEO-01 衛星的影響最大，并且對于地球引力場中的衛星，J2 項的影響會隨著軌道高度的減小而增大，因此，對于高精度時間基準的建立，J2項攝動加速度引起的原時偏差不可忽略。

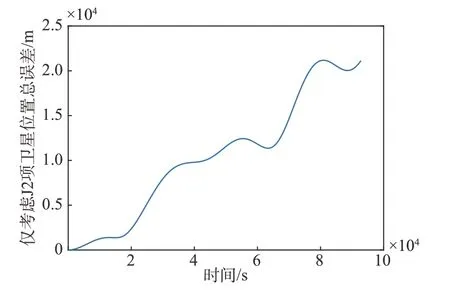
圖5 僅考慮J2項攝動加速度時位置誤差Fig.5 Position error only considering J2 perturbation acceleration

圖6 僅考慮J2項攝動加速度時速度誤差Fig.6 Velocity error only considering J2 perturbation acceleration

3.2 衛星鐘差仿真

本節根據建立的衛星原時模型對衛星鐘差進行仿真分析。仿真中利用衛星運動方程（12）得到衛星狀態，將狀態信息代入式（14）計算得到的原時偏差并將其作為實際鐘差，與考慮J2 項修正的衛星原時模型（17）得到的鐘差進行對比，進而分析模型精度，仿真參數與3.1節相同。

實際鐘差、考慮J2 項修正的模型（17）以及簡化模型（16）的計算結果如圖7 所示。根據仿真結果可知，衛星原時與坐標時的偏差即衛星鐘差隨著時間的增加而增大，在偏心率接近0時，衛星鐘差與坐標時之間近似為線性關系，與文獻［19］結論一致，在兩個軌道周期時，MEO-01 衛星的鐘差已經達到了2.21×10-5s。

圖7 衛星鐘差計算結果Fig.7 Satellite clock difference calculation results

兩種模型的誤差如圖8所示，隨著時間的增加，兩種模型的計算誤差都逐漸增大。在兩個軌道周期內，考慮J2項修正的模型誤差峰值為26.97 ps，簡化模型的誤均差峰值為47.95 ps，兩者比實際鐘差小6個數量級，即兩種模型都能用于計算衛星鐘差。但由于簡化模型未考慮J2 項攝動對衛星原時速率的影響，計算得到的鐘差波動大，誤差的均方根為27.23 ps，而考慮J2 項修正的模型計算結果波動較小，誤差的均方根為16.27 ps，提高了40.26%。仿真結果表明考慮J2 項修正的衛星原時模型可以有效提高衛星鐘差的計算精度。

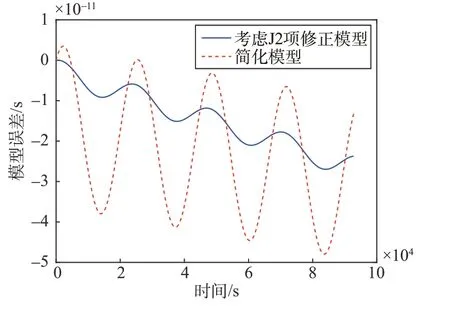
圖8 原時模型誤差Fig.8 Proper time model error

模型（23）為衛星鐘差的軌道要素表示形式，該形式表明J2 項引起的鐘差中包含常值項與周期項，軌道傾角為0°時，常值項達到最大值，此最大值與軌道半長軸成反比；當軌道傾角為54.73°時，常值項為0。周期項的周期為衛星軌道周期的一半，幅值與軌道半長軸及軌道傾角有關。在小偏心率情況下，真近點角可通過軌道平均角速度n近似為：

對周期項積分可得：

周期項幅值與軌道半長軸和軌道傾角的關系如圖9所示，隨著軌道傾角的增加，J2項攝動加速度引起的周期項鐘差逐漸增大，并隨著軌道半長軸的增加而快速減小。

圖9 J2項攝動加速度引起的周期項鐘差幅值與軌道傾角及半長軸關系Fig.9 Relationship between the amplitude of periodic proper time deviation caused by J2 perturbation acceleration，orbital inclination，and semi-major axis

3.3 星間鐘差仿真

3.2 節的衛星原時仿真結果表明，衛星在軌運行期間星載原子鐘會產生鐘差，并且鐘差與衛星軌道相關，進而導致不同衛星間產生星間鐘差。本節對兩衛星間的鐘差進行仿真研究。文獻［19］的研究表明兩衛星軌道半長軸不同時，星間鐘差分為線性與周期項兩部分，線性部分會隨著半長軸差異的增加而迅速累積，但通常衛星發射前都會根據目標軌道對原子鐘進行頻率校正［16］，因此本節只研究衛星軌道半長軸相同的情況下星間鐘差的變化規律，且假設初始時刻星載原子鐘均經過校準，即Δτ0=0。與衛星鐘差仿真相同，仿真中兩顆衛星的狀態由運動方程（12）得到，衛星原時通過式（14）計算，作差后得到實際星間鐘差，與式（25）計算得到的星間鐘差進行對比，分析模型誤差。

仿真中一顆衛星軌道參數與表1 相同，另一顆衛星初始真近點角為180°，即兩衛星軌道面相同，在軌道平面內初始位置相差180°。兩衛星間的鐘差以及模型誤差如圖10 和圖11 所示。仿真結果表明，兩個軌道周期內，模型的計算結果與理論鐘差基本吻合，星間鐘差呈周期性變化，周期與衛星軌道周期相同，仿真中兩顆衛星的鐘差峰值為5.89 ns；模型誤差也近似為周期變化，最大誤差為8.86×10-2ps。

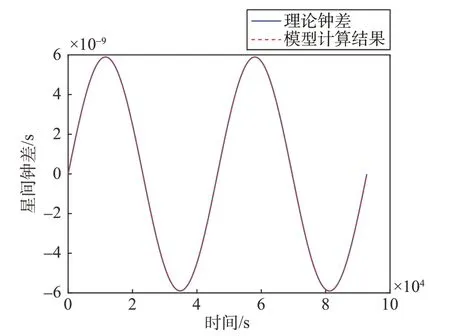
圖10 星間鐘差Fig.10 Inter-satellite clock difference

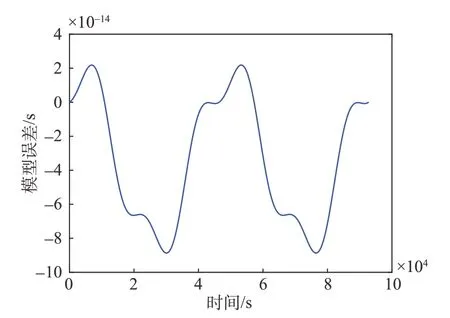
圖11 星間鐘差模型誤差Fig.11 Inter-satellite clock difference model error

為說明J2 項修正的有效性，采用文獻［19］的模型對相同參數的衛星進行星間鐘差仿真，模型誤差如圖12所示。仿真結果表明，無J2項修正的星間鐘差模型誤差隨時間逐漸增大，在兩個軌道周期時，誤差為16.37 ps，遠大于本文提出的考慮J2 項修正的星間鐘差模型的誤差。

除了中軌（MEO）衛星，BDS 星座還包含高軌同步（GEO）衛星及高軌傾斜（IGSO）衛星。美國的GPS星座由近圓形軌道（e=0.02）的中軌衛星組成［6］，選取對應軌道上的一顆衛星，另一顆衛星與其在同一軌道平面上，初始位置相差180°，根據星間鐘差模型計算這兩顆衛星間的鐘差，衛星的軌道參數以及計算結果如表2 所示。根據表2 的仿真結果可以看到，四種軌道平面中星間鐘差峰值從小到大依次為BDS-GEO，BDS-MEO，BDS-IGSO 和GPS-MEO。這是因為隨著軌道偏心率的增加，衛星速度與位置的變化引起的原時偏差增大，進而引起星間鐘差峰值變大。對于BDS-IGSO 和GPS-MEO 這兩個軌道平面，由于其半長軸、偏心率和軌道傾角的影響，兩個軌道平面上衛星受到的太陽及月球的影響較大，而本文建立的星間鐘差模型（25）忽略了其余天體的影響，因此模型誤差的峰值大于其余兩個軌道平面的誤差峰值，但仍在皮秒量級。這些算例的計算結果表明考慮J2 項修正的星間鐘差模型誤差最大在皮秒量級，能夠準確計算星間鐘差。

表2 不同軌道的星間鐘差計算結果Table 2 Calculation results of inter-satellite clock difference in different orbits

4 結論

本文針對新一代導航衛星對高精度時間基準的需求，在廣義相對論體系下建立了衛星的運動方程，考慮地球引力場內衛星受到的J2 項攝動影響，提出了包含J2 項修正的衛星原時模型以及星間鐘差模型，模型能夠有效地計算出衛星在引力場中運動時產生的原時偏差以及星間鐘差。相比基于開普勒軌道假設得到的模型，考慮J2 項修正可以提高衛星原時以及星間鐘差的計算精度。仿真結果表明，衛星運動過程中產生的原時偏差與衛星軌道要素緊密關聯，并隨著時間增加而增大，考慮J2 項修正計算得到的原時偏差與實際鐘差更為接近。同時本文提出的星間鐘差模型能夠在皮秒量級的精度上計算星間鐘差。本文工作可為導航系統的時間基準建立與自主維持提供理論支持。