從生長數學視角看規則下的概念教學

程玉林 吳境川 蔡華遠

摘要：規則下的概念教學要通過問題驅動，讓學生自主探索、創造規則、發明規則，讓規則隨著思維的生長自然地生長出來，從而建立概念.在這一過程中，學生能感受到數學概念的生長過程和數學概念形成的必要性、必然性、客觀性、合理性.

關鍵詞：規則下的概念教學；函數的奇偶性；生長數學

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2024）12-0059-03

數學概念是數學思維的起點，是學生認識的根本，是數學教學的關鍵，它在數學學習與數學教學中具有舉足輕重的作用[1].然而在實際的數學教學中，并沒有把概念教學放在它應有的位置上.通常是“三個例子、一個概念、八項注意”.這樣的數學概念教學，不但給學生數學學習造成認知上的障礙，而且還喪失了數學概念的教學功能，不利于學生數學核心素養的形成.如何讓數學概念教學為學生身心成長助力，讓數學核心素養落地生根，因此數學概念教學十分重要.

1 規則下的數學概念教學理解

發明不同于科學發現，發明主要是創造出過去沒有的事物.規則就是制定規矩，它應該屬于發明.所以，規則下的數學概念教學，重點是制定相應概念準則.但是在平時的教學中，往往將規則下的數學概念教學，變成直接地告訴學生應該遵守的規則并讓其按照規則進行操作，且只是在操作中理解規則的教學，更有甚者不追求理解，只要會操作就可以.這樣的數學概念教學就是一個執行標準的過程，它是一個簡單化的思維過程，顯然這樣來設計規則下的概念課，定是白白浪費了可貴的教學資源.這就是華羅庚先生所說的“入寶山而空返”.現在的問題是，如何入寶山而不空返呢？卜以樓認為，讓學生主動地構建規則制定標準，并且讓學生在生活實踐中有自己的思考，這是一種“制定標準”的“管理者”的思維[2].請注意一個是“執行標準”的“打工仔”的思維，另一個是“制定標準”的“管理者”思維，這兩種思維方式涇渭分明.

2 教學設計與說明

2.1 給情境：導入新課

同學們，我們生活在美的世界中，有許多對美的感受，今天我們就來談一談其中的對稱美，請同學們想一想哪些東西會給你對稱美的認識呢？函數來源于生活，函數中的對稱美又是什么樣的呢？這就是我們本節課要學習的內容：函數的奇偶性.（學生先舉例，教師后在屏幕上給出一組圖片：蝴蝶，喜字，故宮太和殿，雪花晶體.）

觀察1：觀察函數f（x）=x2和g（x）=2-|x|的圖象，它們有什么共同特征？（引導學生從對稱性方面觀察）

說明：給情境.通過以上的圖例和觀察給出問題情境，讓學生運用自己的智力和思維來解決.

2.2 建規則：奇偶性的符號化定義

探究一：我們來繼續研究函數f（x）=x2和g（x）=2-|x|.從圖象上，我們已經看出它們的圖象是關于y軸對稱的.類似于函數的單調性，大家能用數學語言描述“函數圖象關于y軸對稱”這一特征嗎？

問題1：觀察f（x）=x2圖象和課本表3.2-1，你發現函數的解析式具有什么特征了嗎？

師生活動：通常情況下，學生會從表格中觀察到一些數值的變化情況，如：

f（-3）=9=f（3），

f（-2）=4=f（2），

f（-1）=1=f（1），

…………

學生不難發現：當x的取值互為相反數的時候，其函數值總是相等的.

追問1：這種數值的變化情況具有一般性嗎？對任意的x都成立嗎？

追問2：這種對任意的x都滿足的規律，我們可以通過什么方式準確地表達出來？（這時教師要引導學生聯系全稱量詞的表述形式）

追問3：大家嘗試通過量詞的表述，把這個函數的對稱關系表達出來.

問題2：對于函數f（x）=x2圖象關于y軸對稱，這說明函數f（x）=x2圖象上任意兩個點橫坐標如果互為相反數，那么這兩個點相應的函數值相等，即f（-x）=f（x）.反之，如果函數f（x）=x2對任意的自變量x都有f（-x）=f（x），則函數的圖象是否關于y軸對稱？

說明：建規則.這個環節一定要舍得花時間，讓學生做這個看起來與考試無關，可事實上，它不僅與考試有關，更與人的成長有關，它是一個人的核心素養的行為展現.“探究一”學生會遇到困難，這個沒有關系，讓學生帶著疑惑繼續進行下面的思考和研究，這樣他獲得的感受會更深.對于問題2利用數學畫板展示函數圖象關于y軸的對稱關系，展示將整體的對稱關系用任意點的形式動態表達，讓學生通過數學直觀上升到數學抽象，用語言進行描述，進而用符號語言準確的表達.反之，學生會遇到困難，引導學生要證明函數圖象關于y軸對稱，就是相當于證明任一點關于y軸對稱點也在圖象上.

追問：你能將上面由具體函數得到的關系，推廣到一般的圖象關于y軸對稱的函數上嗎？

師生活動：學生不難得到“x∈I，都有f（-x）=f（x）”，但是教師要引導學生注意函數的定義域，逐步完善，并總結出偶函數的定義[3].

一般地，設函數f（x）的定義域為I，如果x∈I，都有-x∈I，且f（-x）=f（x），那么函數f（x）就叫做偶函數.

2.3 偶函數定義的鞏固與辨析

追問：你能再舉出幾個偶函數的例子嗎？（學生舉例）

問題3：函數f（x）=x2，x∈-1，2是偶函數嗎？偶函數的定義域有什么特征？

說明：下定義.引導學生共同討論后，會達成比較相同的意見與結論.得出偶函數的定義.

2.4 奇函數的定義和鞏固辨析

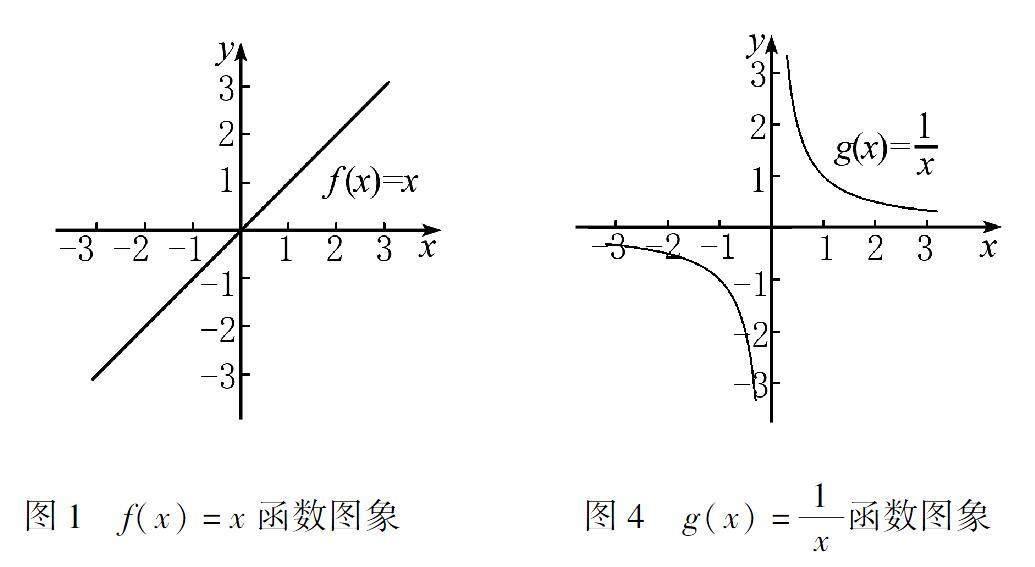
探究二：觀察函數f（x）=x和g（x）=1x的圖象，它們有什么共同特征嗎？同學們能用數學符號語言來描述這一特征嗎？

類比偶函數的研究，考慮下面這幾個問題：

問題4：完成課本表3.2-2，你發現函數的解析式具有什么特征了嗎？

問題5：對于函數f（x）=x，圖象關于原點對稱，表明函數圖象上橫坐標互為相反數的點相應的函數值相反，即f（-x）=-f（x）.反之，如果函數f（x）=x對任意的自變量x有f（-x）=-f（x），那么函數的圖象是否關于坐標原點對稱呢？

問題6：類似于偶函數的定義，請同學們給出奇函數的定義？奇函數的定義域有什么特征？

追問：奇偶性是函數的局部性質嗎？

問題7：有了奇（偶）函數的定義，請問有哪些需要注意的地方？

說明：生長數學視角下的數學概念教學必須關注好、選擇好、應用好生長的種子.所謂“種子”是那些反復強化的數學知識、數學思想方法和數學活動經驗.讓這些數學知識、數學思想方法和數學活動經驗在學生的腦海里烙上深深的印記，就是埋下了種子，等到學生的數學理解能力到位了，數學潛能也就自然而然地發揮出來了，數學核心素養也就自然而然地養成了.

2.5 再運用：函數奇偶性的應用

例1判斷下列函數的奇偶性

（1）f（x）=x4；（2）f（x）=x5；（3）f（x）=xx-1；

（4）f（x）=x+1；（5）f（x）=|x-2|.

變式練習：

判斷對錯：

（1） 若函數f（x）為偶函數，則f（x）=f（-x）；

（2） 若函數f（x）為奇函數，則f（x）=f（-x）；

（3） 奇函數的圖象一定過原點；

（4） 奇函數f（x）在x=0上有意義，則f（0）=0；

（5） 奇函數的圖象關于x軸對稱；

（6） 偶函數的圖象關于y軸對稱；

（7） 若f（x）為奇函數且f（1）=3，則f（-1）=-3.

說明：函數奇偶性的再運用，在教師的引導下，學生自主構建了規則，那么學生就很容易遵守規則了.例6和變式練習就是對學生進行遵守規則的訓練.

2.6 課堂小結

（1）這節課我們研究了函數的什么性質？從哪兩個方面研究的？用了什么方法研究的？

（2）什么是偶函數？什么是奇函數？它們的圖象有什么特征？

（3）判斷函數奇偶性有幾種方法？具體步驟？

說明：本課小結不僅體現了奇偶性的概念、基本性質、圖象特征等知識點的回歸，還滲透了數學思想方法.這是研究函數性質的一般過程的學習方法的總結，是對學生思考、推理過程的總結，也是對函數奇偶性概念規則的構建過程的總結.3 結束語

規則下的數學概念教學是這樣的：給情境-建規則-下定義-再運用.即用問題驅動來激發學生的發明創造，來構建解決數學問題的規則，獲得數學概念和規則，從而把學習數學內化為一種自覺的思維形式.規則下的數學概念教學，課堂上學生要努力做到經歷具體的問題情境，妥善運用創新意識數學邏輯思維，尋找解決數學問題的規則和方法.同時不斷調整優化數學概念的規則和方法，直至發現數學概念的規則和方法，最終建立數學概念.規則下的數學概念教學關鍵就是構建利于學生思維的數學活動，進而讓學生進行發明創造.

參考文獻：

[1]卜以樓.生長數學：卜以樓初中數學教學主張[M].西安：陜西師范大學出版總社，2018（6）.

[2] 王紅兵，卜以樓.生長過程：概念教學的本質標志[J].中學數學教學參考，2017（07）：27-29.

[3] 吳艷芹，馬杰.暢言智慧課堂下的“函數奇偶性”主題教學設計[J].中學數學研究，2023（04）：8-11.

［責任編輯：李璟］