電容器能量公式在強基計劃試題中的應用

黃通

摘要：電容器中存儲的電能及其等價形式，是高校強基計劃考試中的一個考點.電容器中存儲的靜電能可以細分為自能和互能.文章先給出電容器的能量公式，并分析其來龍去脈，然后分析自能和互能以及它們之間的關系，最后給出電容器的能量公式在高校強基計劃考題中的應用.

關鍵詞：電容器；能量公式；自能和互能；強基計劃

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2024）12-0068-03

電容器是一種容納電荷的器件，任何兩個彼此絕緣且相隔很近的導體間都構成一個電容器.電容器有多種，下面主要研究平行板電容器中存儲的電能及其能量公式在高校強基計劃考題中的應用.

1 電容器的能量公式

電容器中存儲的電能為W=12CU2，這就是電容器的能量公式.

由于Q=CU，故它還有另外兩個等價形式：

W=Q22C，W=12QU［1］.

要牢牢記住這個公式， 一般強基計劃的考試中一旦出現， 只需要簡單使用此公式就可以了.

2 自能和互能

靜電能又可以細分為自能和互能.自能是指只有一個帶電體的靜電體系所帶的電能.任何一個帶電物體，可以將其看作由無限多個小塊組成的靜電體系，因此也會有靜電能，這個靜電能就叫作帶電體的自能.如果帶電的物體較多（大于等于兩個），除了帶電體自身引起的自能外，還有一個相互作用能，這個相互作用能就叫作互能.

一般來說，對于多個帶電體組成的系統，其總電能包含以下兩個部分：

（1）每個帶電體的自能.它的大小定義為讓它的每一小塊依次無限遠離時電場力所做的功[2].

（2）各個帶電體之間的互能.它的大小為各個帶電體距離無限遠離時電場力所做的功.

經過推導，我們可以把互能定義為W=12W12+W21，寫成平權形式，是為了便于推廣.推而廣之，如果有3個點電荷系統，則有

W=12W12+W21+W23+W32+W13+W31

=W12+W23+W13.

簡單地說，假定電荷qi在qj處激發的電勢為Uij，則有qjUij=qiUji.比如q2U12=q1U21.以此類推，得總功為

W=12［q1（U21+U31）+q2（U12+U32）+q3（U13+U23）］

令U1=U21+U31，U2=U12+U32，U3=U13+U23，則

W=12q1U1+q2U2+q3U3=12∑3i=1qiUi.

推廣可知，n個點電荷系統的互能為

W=12∑ni=1qiUi.

特別注意，式中Ui為qi所在處除qi以外的其他電荷所產生的電勢.

如果我們畫個圈，把上面討論中的q1，q2和q3全部囊括進去，使其變成一個帶電體A的 3個組成部分，這樣上面討論中得到的W=12∑3i=1qiUi就是A的自能了.

3 自能和互能的關系

就像研究運動時要說明參考系一樣，在研究靜電能時也要說明要研究的對象到底是點電荷還是一個帶電體.如圖2所示的3個點電荷，我們做兩種處理來比較：

（1）將每個獨立的點電荷看作一個“子系統”，整個體系的靜電能等于3個點電荷的自能和它們之間的互能之和.

（2）將q1和q2合起來看作一個“子系統”，而q3視作另一個“子系統”，整個系統的靜電能等于兩個子系統的自能和它們之間的互能之和.

很明顯，兩次的自能和互能都不相等，但是自能和互能之和是相同的.如果系統中有點電荷q，除了它還有許多其他的電荷，假定q在其他電荷共同激發的電場中運動，再假設在q運動的過程中q和其他電荷的電荷分布均不改變，即q和其他電荷的自能均不改變.我們把眼光緊緊盯著q，如果它在加速，則根據能量守恒可知，它增加的動能必然來源于兩個子系統之間的互能的減少量.而我們又知道q動能的增加量等于系統勢能的減少量.這樣就自然可以得：到子系統互能的減少量=系統勢能的減少量.

所以點電荷q在電場中一點的勢能就是點電荷q在外電場中一點的互能，即并未包括q的自能.

將以上的點電荷系統推而廣之，自然只需要考慮體系中互能的變化量，前提是自能不發生變化，即帶電體的電荷分布不改變.但實際上是很難保持電荷分布不變的，例如由兩個導體組成的帶電系統，由于遠近不同，其上分布的電荷肯定會有所變化，這個時候再把導體整體作為一個子系統，其自能就必然會變化.

這樣一想，我們不如把每個微元電荷作為一個子系統，這樣每個子系統的自能就自動為零，所有的靜電能全為互能，并且所有的“導體系”也不再成立，變成了“點電荷系”.這樣，總的靜電能自然是W=12∑ni=1qiUi，其中Ui為qi所在處除qi以外的其他電荷所產生的電勢.

如果只有一個帶電體，它的靜電能可做如下定義： 設想將該帶電體分割成無限多的電荷元，把所有電荷元從現有的集合狀態彼此移送至無限遠處，則電場力所做的功即為此帶電體的自能.可用下式表示：W=12∫qUdq.

4 在強基計劃試題中的應用

例1一絕緣的均勻帶電球體，其半徑為R，總電荷為Q，求其靜電能.

解導體內、外的電場分布為

E1=kQR3r（rR），

球內取r→r+dr的薄球殼， 電量為

dQ=ρdV=Q43πR3·4πr2dr=3QR3r2dr，

電勢為

U=∫RrkQR3rdr+∫

SymboleB@

RkQr2dr=kQ2R33R2-r2，

所以靜電能為

W=12∫UdQ=12∫R0kQ2R33R2-r2·3QR3r2dr

=3kQ25R.

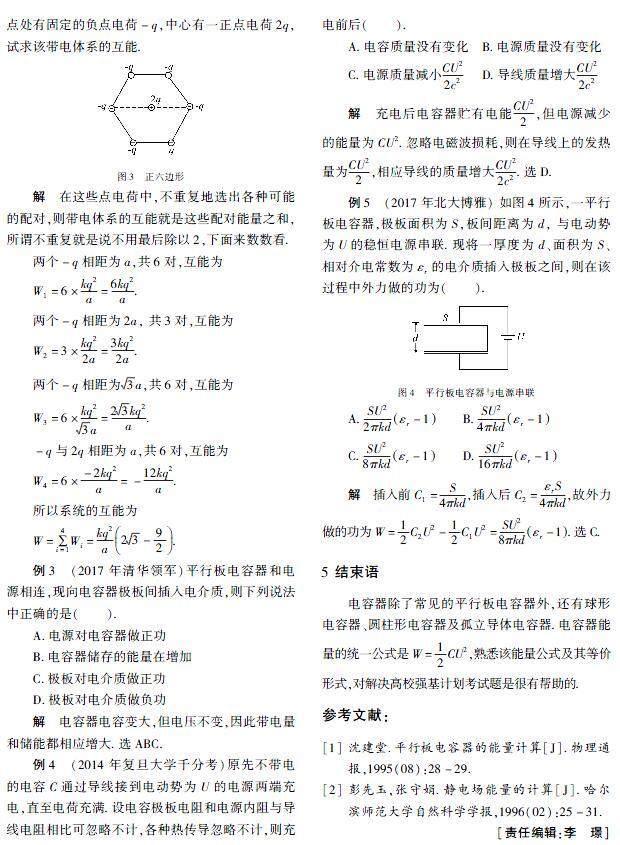
例2如圖3所示，正六邊形的邊長為a，各頂點處有固定的負點電荷-q，中心有一正點電荷2q，試求該帶電體系的互能.

解在這些點電荷中，不重復地選出各種可能的配對，則帶電體系的互能就是這些配對能量之和，所謂不重復就是說不用最后除以2，下面來數數看.

兩個-q相距為a，共6對，互能為

W1=6×kq2a=6kq2a.

兩個-q相距為2a， 共3對，互能為

W2=3×kq22a=3kq22a.

兩個-q相距為3a，共6對，互能為

W3=6×kq23a=23kq2a.

-q與2q相距為a，共6對，互能為

W4=6×-2kq2a=-12kq2a.

所以系統的互能為

W=∑4i=1Wi=kq2a23-92.

例3（2017年清華領軍）平行板電容器和電源相連，現向電容器極板間插入電介質，則下列說法中正確的是（）.

A.電源對電容器做正功

B.電容器儲存的能量在增加

C.極板對電介質做正功

D.極板對電介質做負功

解電容器電容變大，但電壓不變，因此帶電量和儲能都相應增大.選ABC.

例4（2014年復旦大學千分考）原先不帶電的電容C通過導線接到電動勢為U的電源兩端充電，直至電荷充滿.設電容極板電阻和電源內阻與導線電阻相比可忽略不計，各種熱傳導忽略不計，則充電前后（）.

A.電容質量沒有變化

B.電源質量沒有變化

C.電源質量減小CU22c2

D.導線質量增大CU22c2

解充電后電容器貯有電能CU22，但電源減少的能量為CU2.忽略電磁波損耗，則在導線上的發熱量為CU22，相應導線的質量增大CU22c2.選D.

例5（2017年北大博雅） 如圖4所示，一平行板電容器，極板面積為S，板間距離為d， 與電動勢為U的穩恒電源串聯.現將一厚度為d、面積為S、相對介電常數為εr的電介質插入極板之間，則在該過程中外力做的功為（）.

A.SU22πkdεr-1B.SU24πkdεr-1

C.SU28πkdεr-1D.SU216πkdεr-1

解插入前C1=S4πkd，插入后C2=εrS4πkd，故外力做的功為

W=12C2U2-12C1U2=SU28πkdεr-1.

選C.

5 結束語

電容器除了常見的平行板電容器外，還有球形電容器、圓柱形電容器及孤立導體電容器.電容器能量的統一公式是W=12CU2，熟悉該能量公式及其等價形式，對解決高校強基計劃考試題是很有幫助的.

參考文獻：

[1]沈建堂.平行板電容器的能量計算[J].物理通報，1995（08）：28-29.

[2] 彭先玉，張守娟.靜電場能量的計算[J].哈爾濱師范大學自然科學學報，1996（02）：25-31.

［責任編輯：李璟］