蹺板式面板開關觸點接觸壓力一致性參數優化研究*

□ 竺振韜 □ 常秋香 □ 王賢成 □ 余林茂

1.寧波大學 機械工程與力學學院 浙江寧波 315211

2.寧波大學科學技術學院 浙江慈溪 315300

3.寧波公牛電器有限公司 浙江慈溪 315300

1 研究背景

面板開關為機械式結構,操作簡便,外觀精美,是日常生活中普遍使用的電路控制設備,在低壓電器行業中具有較高的市場占有率。國內面板開關研究相較于繼電器、斷路器等低壓電器,設計理論不完善,產品設計大多采用仿制和經驗模式。國內企業在批量生產過程中,產品壽命的分散性大,影響人們的日常使用安全[1]。合理的參數組合設計可以保證產品性能要求,公差會影響性能波動范圍,設計最佳參數組合并提高公差精度,產品的一致性必然會得到提高。對于低價格且大批量生產的產品而言,改善關鍵零件的公差,則生產中成本較高。

在現有的研究中,Del Casale等[2]采用參數設計和容差設計方法,確定閉環控制器的最佳參數組合。陳昊等[3]基于Stoner-Wohlfarth模型和Preisach模型,獲得非線性永磁體局部磁滯曲線,結合徑向基函數提高質量一致性。周月閣等[4]建立基于退化失效時間準則的優化模型,降低功率變換器性能退化敏感性。劉曉明等[5]建立考慮公差不確定性的斥力操動機構保持單元多目標優化設計模型,基于非支配排序粒子群算法的多變量多目標優化方法,獲得參數設計公差。目前的研究主要為設計最佳性能,并通過容差設計保證一致性。上述研究通過重新設計容差提高一致性。綜合考量下,提高容差勢必使成本增加,因此更傾向于采用產品現行公差進行參數優化設計,提高優化目標的一致性。

國內企業對面板開關一致性影響顯著的關鍵設計參數組合無法確定,對此,根據性能一致性和大批量生產中的成本控制要求進行研究[6]。低壓電器電壽命與電性能相關,電性能主要包括觸點接觸電阻[7]、熔焊電流[8]、溫升[9]等。觸點接觸壓力與電路通斷性能直接相關,是電性能的重要影響參數,受結構設計參數影響較大[10-12]。筆者以某型號蹺板式面板開關為研究對象,提高觸點接觸壓力一致性。分析面板開關工作原理,確定影響參數。通過有限元仿真,計算觸點接觸壓力。根據企業現行設計公差,設計正交試驗,獲取影響因素貢獻率。采用Kriging模型建立輸入參數與觸點接觸壓力的近似模型,結合非線性二次規劃算法確定輸出特性在設計公差下的最小波動值,進而確定參數組合。

2 蹺板式面板開關工作原理

蹺板式面板開關的主要部件包括按鈕、過渡件、壓板、彈簧、彈子、蹺板、動靜觸點、支撐片、連接片和端子等,結構如圖1所示。

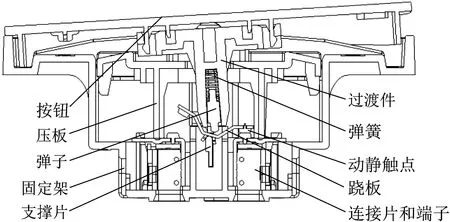
圖1 蹺板式面板開關結構

面板開關根據功能,主要可分為輔助機構、傳動機構、執行機構。輔助機構滿足用戶審美、固定安裝、內部機構保護作用。傳動機構由按鈕、過渡件、壓板、彈簧、彈子組成,用于力傳遞,將外部驅動力改變為合適的執行機構驅動力。執行機構由動靜觸點、蹺板、支撐片、連接片和端子組成,用于實現電路通斷。

觸點接觸過程可分為動態接觸過程和靜態接觸過程。在彈簧系統推動下,彈性勢能轉換為動觸點的動能。動靜觸點接觸,大部分動能轉換為觸點表面材料的彈性變形和塑性變形。在動態接觸過程中,動能和彈性勢能來回轉換,轉換中伴隨能量損耗,最終從動態接觸轉變為靜態接觸。

由彈性力學接觸理論和動能守恒定理,觸點碰撞接觸壓力表示為[13-14]:

F=kδ3/2

(1)

(2)

(3)

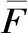
觸點穩定接觸由彈簧變形保證,根據力矩計算式,彈簧彈力和觸點接觸壓力的關系式為:

F=D2/D1×Fecosθ

(4)

式中:Fe為彈簧彈力;D1為觸點接觸壓力力臂;D2為彈力力臂;θ為彈力偏移角度。

通過上述分析,觸點接觸壓力與觸點間距、蹺板轉動角度、彈簧壓縮距離、彈子作用位置等因素有關。根據零件設計圖,將靜觸點高度、支撐片高度、蹺板間距作為輸入參數。

3 執行機構仿真模型

面板開關主要由注塑件和金屬件組成,注塑件優化開模成本高,因此將金屬件作為優化部件。執行機構為金屬件,將其作為優化部件。觸點接觸壓力測量需要破壞面板開關外殼,對此,采用仿真分析計算。基于零件圖紙和產品實測數據,獲取零件尺寸和空間位置,通過SolidWorks軟件建立執行機構三維模型,如圖2所示。

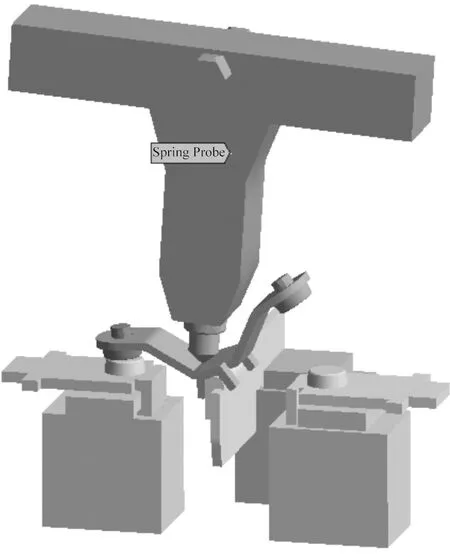
圖2 執行機構三維模型

將執行機構三維模型導入ANSYS Workbench軟件,利用瞬態結構分析模塊進行動力學仿真。對模型添加材料,根據接觸面連接方式設置綁定接觸、摩擦接觸,對過渡件添加轉動副,對彈子和過渡件添加平移副和彈簧連接,對彈簧設置1.2 N/mm剛度、12 mm自由長度,加載方式選擇過渡件旋轉角度代替外部驅動,對其它零件添加固定、位移約束,然后進行計算求解觸點接觸壓力。執行機構建模流程如圖3所示。

圖3 執行機構建模流程

根據仿真結果,不同尺寸參數組合下觸點接觸壓力波動較大,觸點接觸壓力經歷陡增、跳動、增長、穩定四個階段。觸點跳動過程彈簧仍在釋放彈性勢能,起到抑制作用,觸點跳動幅度較小。動觸點初速度越大,靜態接觸壓力越大。觸點接觸壓力曲線如圖4所示,仿真和實測誤差約為5%。

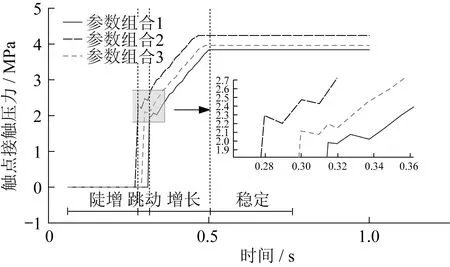
圖4 觸點接觸壓力曲線

4 試驗設計

試驗設計可以最大限度獲得有效信息,識別每個輸入變量對全局目標響應的影響[15-16]。影響輸出特性的因素很多,考慮成本和實際情況,結合模型結構和動力學分析,選取靜觸點高度、支撐片高度、蹺板間距作為輸入變量。

采用正交試驗設計,將三個輸入變量記作因素A、因素B、因素C,將現有設計值作為中心值,根據零件強度要求、工藝要求、生產經驗確定參數模糊區間,控制優化加工成本,以現行加工精度為約束節點。

正交試驗中,為確定最佳參數組合,以粗加工公差作為邊界值,對公差上下限各增加一個水平,試驗因素水平表見表1,第一水平為參數下邊界,第二水平為參數中心值減參數偏差,第三水平為參數中心值,第四水平為參數中心值加參數偏差,第五水平為參數上邊界。

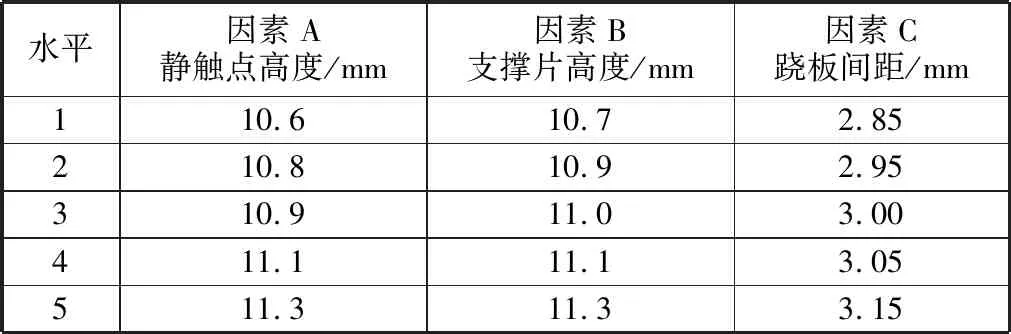
表1 試驗因素水平表

通過正交試驗,分析各因素對觸點接觸壓力的影響,不考慮各因素之間的相互作用。采用L25(53) 正交表,需進行25次試驗,獲得動靜觸點間接觸壓力輸出特性值。正交試驗結果見表2,μ1～μ5表示對應水平下的輸出特性均值,Delta表示各因素五水平試驗均值極差,反映各因素對輸出特性的影響程度。對于觸點接觸壓力,影響因素從主到次排序為支撐片高度、靜觸點高度、蹺板間距。均值主效應圖如圖5所示。

表2 正交試驗結果

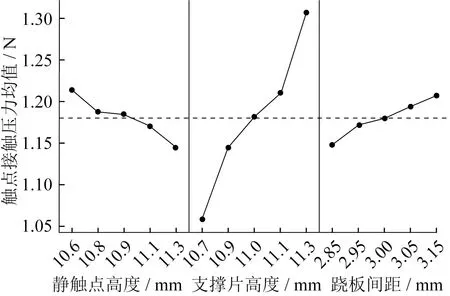
圖5 均值主效應圖

5 Kriging模型

正交試驗通過特殊試驗組數確保試驗的均衡性和有效性,未包含所有水平組合情況,需建立輸入變量與輸出特性關系進行預測。Kriging模型是一種用于插值和預測的統計模型,根據采樣點數據建立輸入與輸出參數之間的函數關系,對輸入量進行快速計算,避免煩瑣的仿真計算求解[17]。Kriging模型相較于響應面模型等對高維非線性問題擬合效果較好,相較于人工神經網絡所需樣本數量少。Kriging模型建模是對目標函數在求解區域內尋求最優無偏估計的過程,建立靜觸點高度、支撐片高度、蹺板間距與觸點接觸壓力的關系函數。Kriging模型表達式為[18]:

(5)

(6)

rT(γ)=[R(γ,γ1),R(γ,γ2),…,R(γ,γm)]T

(7)

(8)

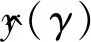
模型擬合度誤差分析為0.95,預測效果較好。擬合度誤差分析表達式為:

R2=SSR/SST=1-SSE/SST

(9)

(10)

(11)

(12)

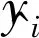
6 優化模型

對蹺板式面板開關的觸點接觸壓力一致性進行優化,在不改變結構形狀和參數公差精度的前提下,對參數組合進行優化,要求觸點接觸壓力波動最小。觸點接觸壓力最小值為1.1 N,限制參數邊界和參數公差值。目標函數為min(Δyi),約束為:

ymin≥1.1 N

10.6 mm≤A≤11.3 mm

10.7 mm≤B≤11.3 mm

2.85 mm≤C≤3.15 mm

ΔA=0.3 mm

ΔB=0.2 mm

ΔC=0.1 mm

Δyi為各參數組合下的波動值,ymin為輸出特性最小值,A為因素A,B為因素B,C為因素C,ΔA、ΔB、ΔC為各因素公差。

7 優化流程

采用非線性二次規劃算法,求解獲取輸出特性波動值的最大值和最小值。非線性二次規劃算法利用二次規劃,將原始的非線性規劃問題轉換為一系列二次規劃子問題,并通過求解這些二次規劃子問題來逼近最優解[19-20]。對因素A、因素B、因素C以各自公差進行分組,并進行排列組合,確定參數區間,經非線性二次規劃算法獲得輸出特性最大最小值,計算確定最小輸出特性波動范圍和最佳參數組合。參數優化流程如圖6所示。為減少計算次數,進行分級優化,根據參數優先級確認最佳組別,計算次數從nk1減少至k1n,n為參數組別數,k1為參數數量。

圖6 參數優化流程

8 優化結果

通過非線性二次規劃算法,求解獲得不同參數下的觸點接觸壓力值波動范圍。根據參數影響優先級,將因素B作為首要約束條件,因素B影響下的觸點接觸壓力在B2至B5范圍內波動相近,在B1范圍內波動最小。結合最小觸點接觸壓力設計需求,選取B4(10.9～11.1 mm)作為支撐片高度尺寸區間。在因素B約束條件下,計算因素A約束下的觸點接觸壓力變化,從A1至A5觸點接觸壓力波動呈減小趨勢,選取A5(11～11.3 mm)作為靜觸點高度尺寸區間。因素A、因素B確定后,C1范圍內觸點接觸壓力波動最小,C4范圍內觸點接觸壓力波動最大,選取C1(2.85～2.95 mm)作為蹺板間距尺寸區間。各因素組合下觸點接觸壓力波動見表3。A1至A5的中心值分別為10.7 mm、10.8 mm、10.9 mm、11.0 mm、11.1 mm,B1至B5的中心值分別為10.8 mm、10.9 mm、11.0 mm、11.1 mm、11.2 mm,C1至C5的中心值分別為2.90 mm、2.95 mm、3.00 mm、3.05 mm、3.10 mm。

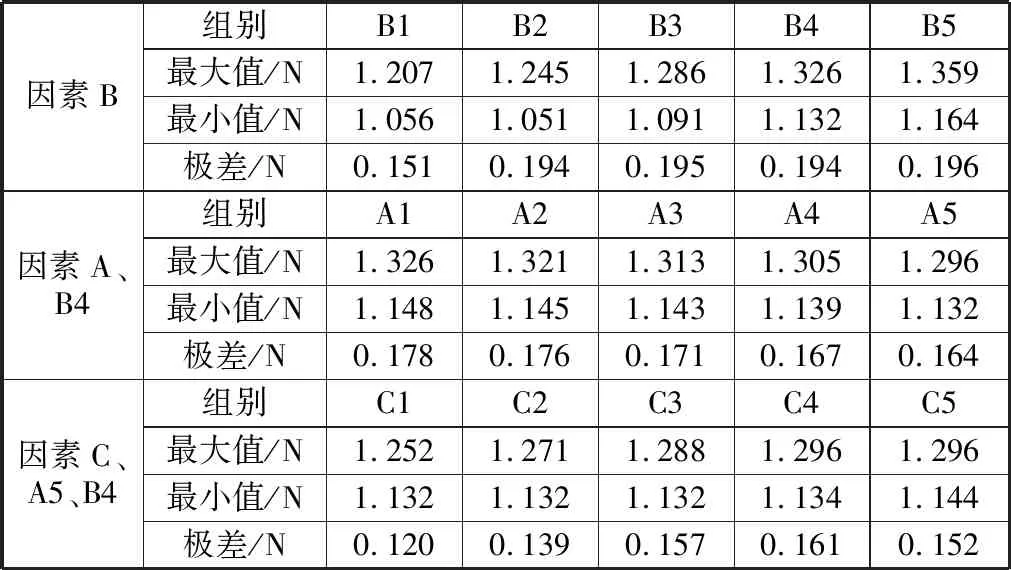
表3 各因素組合下觸點接觸壓力波動

因素B約束下輸出特性波動如圖7所示,因素A和B4約束下輸出特性波動如圖8所示, 因素C和A5、B4約束下輸出特性波動如圖9所示,輸出特性波動重疊如圖10所示。

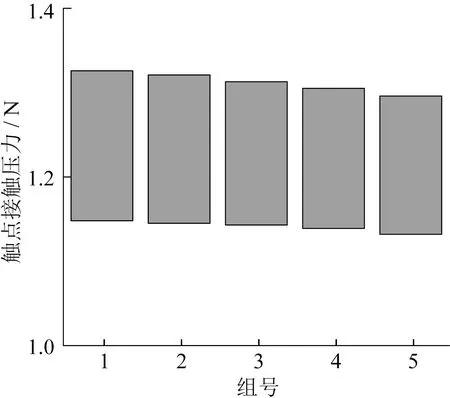
圖7 因素B約束下輸出特性波動

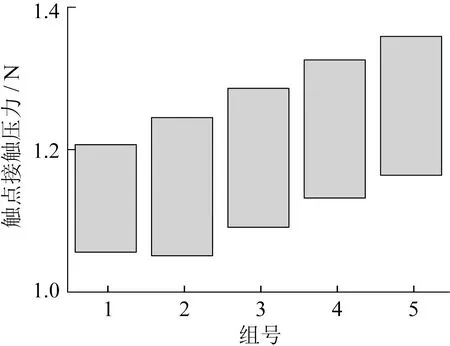
圖8 因素A和B4約束下輸出特性波動

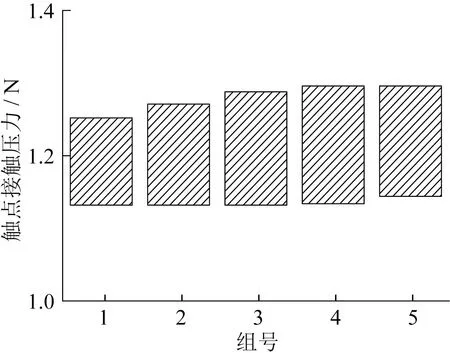
圖9 因素C和A5、B4約束下輸出特性波動

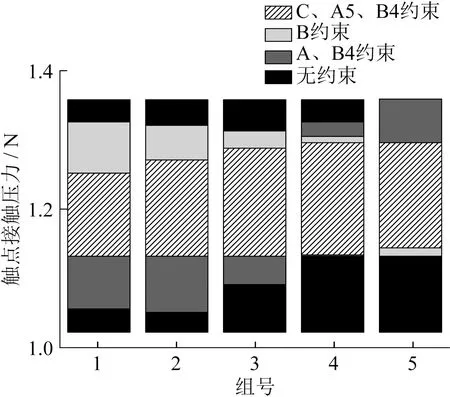
圖10 輸出特性波動重疊

選取A5、B4、C1作為觸點接觸壓力優化組合,優化前后對比見表4。模型計算觸點接觸壓力波動范圍減小14.9%。通過試制樣品實際測量,觸點接觸壓力從1.11～1.25 N變為1.12～1.19 N,波動減小50%。實際測量裝置如圖11所示。

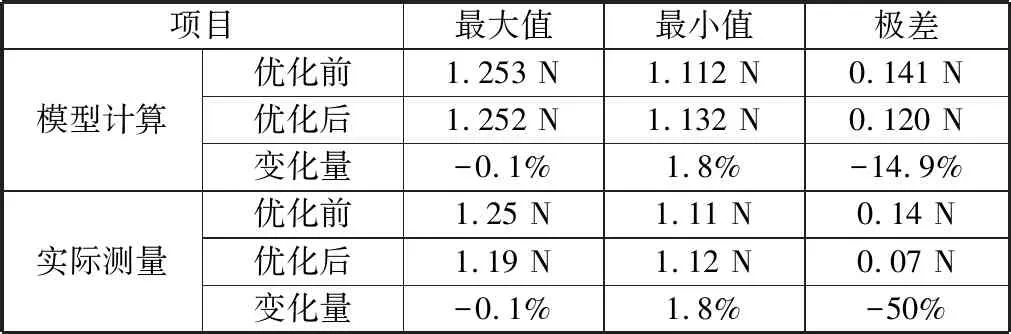
表4 觸點接觸壓力優化前后對比

圖11 實際測量裝置

9 結束語

筆者選取蹺板式面板開關的執行機構作為研究對象,對動靜觸點間的接觸壓力進行有限元分析。針對觸點接觸壓力一致性問題,采用正交試驗、Kriging模型、非線性二次規劃算法等進行分析優化。

在蹺板式面板開關執行機構中,靜觸點高度、支撐片高度、蹺板間距對觸點接觸壓力影響顯著,貢獻率從高到低為支撐片高度、靜觸點高度、蹺板間距。

在企業現行設計公差條件下,最佳性能參數組合并非性能一致性最佳參數組合,觸點接觸壓力一致性提高50%。

筆者計算模型將參數轉換為線性關系,實際參數為離散點,計算模型與實際數值存在偏差,但能反映數值變化趨勢,為產品設計提供參考。如果最佳輸出特性的參數組合和一致性的參數組合相同,那么為進一步提高輸出特性一致性,需提高參數公差或對結構進行優化。