用數(shù)組模型解決“移拼倒三角形”問題

殷素文

［摘 ?要］ 文章以棋子移動為例，把生活中貌似復雜錯亂的圖形變化題，用數(shù)組模型的方法進行解答，使之既有序又簡約，更好地體現(xiàn)用數(shù)學模型解題的高效性和優(yōu)越性，從而培養(yǎng)、激發(fā)學生的模型意識，提升學生的數(shù)學核心素養(yǎng)。

［關鍵詞］ 數(shù)學模型；數(shù)組；轉(zhuǎn)化

小學數(shù)學蘇教版五年級下冊“解決問題的策略”把兩種典型的數(shù)列求和問題運用轉(zhuǎn)化的策略進行教學，即把等差數(shù)列轉(zhuǎn)化成梯形，把等比數(shù)列（比值是0.5）轉(zhuǎn)化成正方形。這兩種轉(zhuǎn)化的策略是由數(shù)到圖的典型應用，屬于計算技巧的類別。現(xiàn)實生活中經(jīng)常遇到由文字表達或圖形呈現(xiàn)出的問題，探尋這些問題背后的數(shù)學模型，實現(xiàn)由圖到數(shù)的思維提升，可以助力學生更高效地解決問題。

一、網(wǎng)絡小視頻，問題在身邊

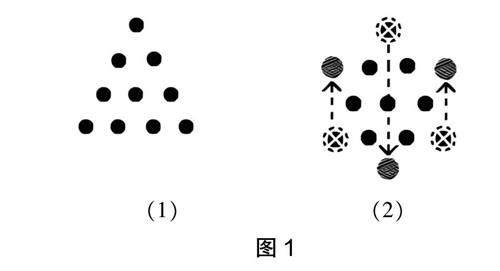
網(wǎng)絡小視頻有一道題：如圖1（1），請在10秒內(nèi)，只移動3顆棋子，使圖形變成倒三角形。解題圖示見圖1（2）。

很多網(wǎng)友挑戰(zhàn)失敗，在解題過程中棋子既有上移又有下移，容易干擾思維。當多次刷到這個視頻時，筆者逐漸產(chǎn)生以下想法：

①這只是一道簡單的棋子移動問題嗎？可不可以用數(shù)學方法來解決？

②最少只需要移動3顆棋子嗎？

③如果是一個5層、6層以及更多層結構的三角形，最少需要移動多少顆棋子？

④這種研究方法對于其他圖形有沒有通用性？

帶著這樣的問題，筆者開始了“移拼倒三角形”背后的數(shù)學模型的探究。

二、過程再還原，有序更清晰

《福爾摩斯探案》是受青少年喜愛的偵探小說之一，當案件偵破遇到困難的時候，探員便使用“現(xiàn)場還原”技法進行案件偵破，并屢試不爽。“重回”案發(fā)現(xiàn)場，有助于從源頭剖析案件各要素特點、邏輯關系以及推測事件進展的可能性［１］。同樣，在研究“移拼倒三角形”過程中，筆者以網(wǎng)絡視頻中的4層結構三角形為例，還原移拼過程，以利于觀察其中的變化規(guī)律，抽絲剝繭，進而提煉問題背后的數(shù)學方法。

因為研究需要移動的最少棋子數(shù)，就一定存在不需要移動的最大棋子數(shù)，也就是移動前與移動后的兩個三角形存在最大的重疊棋子數(shù)，這樣就只需要觀察兩個三角形可能存在的不同位置情況，并結合這些情況，用合理的數(shù)學模型來研究棋子的移動情況，這樣研究起來就要理性、快捷得多。

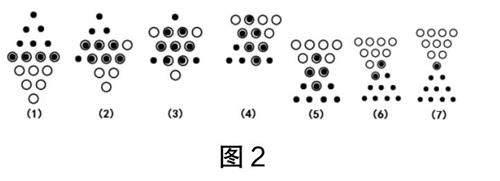
圖2中，用實心圓表示原來的三角形，用空心圓表示移動后的倒三角形。兩個三角形先用棋子數(shù)為4的2層重疊，然后倒三角形逐層上移，直至棋子數(shù)為1的2層重疊。兩個三角形的重疊部分表示不需要移動的棋子，剩下的實心圓數(shù)量就是需要移動的棋子數(shù)量。圖2（1）到圖2（7）中重疊部分的棋子數(shù)分別為4、6、7、6、4、2、1顆，則需要移動的棋子數(shù)分別為6、4、3、4、6、8、9顆。不難發(fā)現(xiàn)，圖2（3）中重疊棋子數(shù)最多，同時也是需要移動棋子數(shù)最少的，只需要移動3顆棋子。圖形分析到這里好像已經(jīng)找到了最少移動棋子的方法，但這種方法無疑會消耗學生較多的時間和精力，雖簡單但無趣。

三、數(shù)組作模型，簡易又形象

《孫子算經(jīng)》認為數(shù)學是天地萬物最根本的東西。現(xiàn)代社會的一切信息都可以用“數(shù)字化”來表示和加工，推動現(xiàn)代社會進步的也是一系列的數(shù)據(jù)計算［２］。那么“移拼倒三角形”問題必然可以用數(shù)學的方法來探究背后的奧秘。

根據(jù)三角形棋子的空間形式和數(shù)量關系，可以把移動前的三角形棋子分布抽象得出數(shù)組，移拼后的倒三角形也可以表示為數(shù)組，接下來只要研究兩個數(shù)組在重疊層數(shù)不同的情況下，重疊的棋子數(shù)及需要移動的棋子數(shù)，問題就簡單多了。圖2的7種情況可以用7個新的數(shù)組來表示（如圖3）：

圖3中每個新數(shù)組的左列數(shù)據(jù)表示原來的三角形棋子，右列表示移拼后的倒三角形棋子。當同一行中兩列數(shù)據(jù)都出現(xiàn)，說明兩個三角形有重疊的部分，重疊數(shù)的大小取兩個數(shù)據(jù)中的較小數(shù)。同一行中，當左列數(shù)據(jù)比右列數(shù)據(jù)大，說明多出的棋子數(shù)就是原三角形需要移動的棋子數(shù)。如圖3（1）中第一、二、三行（從上往下數(shù)，下同）左列數(shù)據(jù)比右列大，需要移動的棋子數(shù)就是：1+2+3=6（顆），圖3（5）中，第四、五行左列數(shù)據(jù)比右列大，需要移動的棋子數(shù)就是：3-1+4=6（顆）。這樣一來，研究“移拼倒三角形”問題就轉(zhuǎn)化成兩個數(shù)組在重疊層數(shù)不同的情況下，同一行中左列數(shù)據(jù)大于右列數(shù)據(jù)的情況，再進行求和，這樣，思維效率就提高了很多。

從圖3中可以得出：4層結構的三角形移拼成倒三角形，當重疊層數(shù)為3時，需要移動的棋子數(shù)是：1+4-2=3（顆），最少。因為從圖3（5）開始，同一行中左列數(shù)據(jù)大于右列數(shù)據(jù)是增加趨勢。因此，在圖3中，分析4層結構的“移拼倒三角形”問題，當重疊層數(shù)達到4層時，后面的情況可以排除，不再分析。

接下來用數(shù)組模型研究5層結構的“移拼倒三角形”問題中出現(xiàn)的情況及最少移動棋子數(shù)。

從圖4（3）可以得到，需要移動的棋子數(shù)為：1+2+5-3=5（顆），圖4（4）中需要移動的棋子數(shù)為：1+4-3+5-2=5（顆），結合圖形可以確定，這兩種方法都是移動棋子數(shù)最少的，棋子的實際分布情況如圖4（6）和圖4（7），數(shù)組模型的結論符合實際情況。

四、數(shù)據(jù)重整合，效率再提高

數(shù)學研究的特點之一是可以進行算法優(yōu)化，即在獲取新的知識或技能后，可以重新組織已有的知識結構使之不斷改善自身的性能，實現(xiàn)對數(shù)據(jù)模型的優(yōu)化重建。

為了更快地探究不同重疊層數(shù)時需要移動的棋子數(shù)，對圖4（1）到圖4（5）的數(shù)組進行重建。通過觀察不難發(fā)現(xiàn)，可以將左邊的數(shù)列看作是固定的，將右邊的數(shù)列看作是自下而上的移動，把不同情況的右列數(shù)合并在同一數(shù)組中，得到圖5。

圖5中帶圓圈的數(shù)字表示通過計算后需要移動的棋子數(shù)，用這種數(shù)組重建的簡化方法把求解的效率提高了很多。這種用數(shù)組的方法解答“移拼倒三角形”問題很容易推廣到6層、7層等結構的三角形。

五、由數(shù)回到圖，呈現(xiàn)方完美

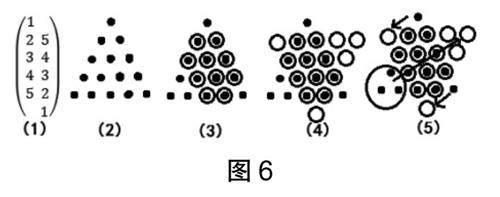
從上面的數(shù)組分析，可以快速得到原三角形與倒三角形存在的重疊層數(shù)，以及需要移動的棋子數(shù)。筆者以圖4（4）的情況為例，示范由數(shù)組回到圖形，給出最終移動棋子的方法。

圖6（1）是兩個三角形的數(shù)組模型。在原來的三角形圖6（2）中，首先，根據(jù)同一行中左列數(shù)據(jù)比右列數(shù)據(jù)小，說明左列該行棋子不要移動的原理，圈出圖6（3）中的上面第2、3層；其次，根據(jù)右列數(shù)據(jù)比左列數(shù)據(jù)小，說明右列該行只要這幾顆棋子，且盡量居中，呈逐步收縮狀排布，圈出圖6（3）中的下面2層；第三，根據(jù)最終倒三角形棋子的排布，補充出倒三角形需要的棋子，如圖6（4）中的空白圓圈；最后，對照原三角形多出的棋子和倒三角形需要補充的棋子，進行移動，最終得出移拼的結果，如圖6（5）。

至此，用數(shù)組模型解決“移拼倒三角形”問題已全景呈現(xiàn)，這種應用是對圖形中數(shù)據(jù)的抽象與提煉，是圖形到數(shù)學模型的轉(zhuǎn)化。

六、追根溯源，問題背后的問題

在探究“移拼倒三角形”問題的時候，通過逆向推導發(fā)現(xiàn)決定最少移動棋子數(shù)的關鍵變量是兩個三角形的重疊層數(shù)，即重疊層數(shù)決定重疊的棋子數(shù)，重疊的棋子數(shù)決定需要移動的棋子數(shù)。雖然重疊層數(shù)是一個變量，總存在著一個重疊層數(shù)，可以導出最少的移動棋子數(shù)，但圖4（6）和圖4（7）的情況又與這一結論相悖，因此這一問題的背后一定關聯(lián)著一個更深或暫且未知的問題。

聯(lián)想到正弦函數(shù)圖象及函數(shù)極值相關的內(nèi)容，圖4（6）和圖4（7）的重疊層數(shù)相等，說明這兩種情況應該是極值兩端的某個相等值，就像圖2（2）與圖2（4）或圖2（1）與圖2（5）。難道5層結構的三角形重疊層數(shù)應為3.5（或為其他小數(shù)）層？但三角形棋子分布中，3.5層就是中間的空格地帶。

仔細推敲一下，人們平時表述的三角形是一個密鋪的圖形，中間不存在空域。三角形棋子分布只是完整三角形的抽象表達，這樣一來整個問題就清晰了：三角形棋子是被局限于整數(shù)的原三角形的抽象表達，“移拼倒三角形”問題的原型是兩個三角形的最大重疊面積問題。最大重疊面積導致非重疊面積最小，最大重疊面積又是由某個重疊高度所決定，只不過這個重疊高度在一般三角形里表現(xiàn)為唯一值，在三角形棋子中可以表現(xiàn)為這個重疊高度的兩個相鄰整數(shù)。至此，“移拼倒三角形”問題完成了“認祖歸宗”。

當然，如果設定參數(shù)，用方程或通過編程的方式也能解決倒三角形的移拼問題，在小學階段暫且探究到這個程度。用數(shù)組模型解決“移拼倒三角形”問題的重要性在于：這種思維方式能夠培養(yǎng)學生用數(shù)學的眼光觀察身邊事物的習慣，培養(yǎng)學生的模型意識，提高學生用數(shù)學模型解決問題的能力，提升學生的數(shù)學核心素養(yǎng)。

參考文獻：

［１］ 宗曉榮. 試析小學數(shù)學教學中數(shù)學模型思想的融入［Ｊ］. 天津教育，２０２０（１１）：１７６－１７７.

［２］ 柯黎青. 小學數(shù)學教學中融入模型思想的探討［Ｊ］. 考試周刊，２０１９（１３）：８９.