微元法在高中物理解題中的應(yīng)用例析

李圓圓

【摘要】微元思想是中學(xué)物理中的重要思想.所謂微元思想，是將研究對象或者物理過程分割成無限多個(gè)無限小的部分，先取出其中任意部分進(jìn)行研究，再從局部到整體綜合起來加以考慮的科學(xué)思維方法.本文從高中物理中的幾個(gè)難點(diǎn)問題入手，探討微元法在高中物理解題中的應(yīng)用.

【關(guān)鍵詞】高中物理；微元法；變力做功

1 微元法在解決變力做功中的應(yīng)用

變力對物體做功時(shí)，很難用功的定義求解變力對物體做的功.當(dāng)力的大小不變，僅方向隨位移發(fā)生變化時(shí)，這類變力做功問題可用微元法求解.

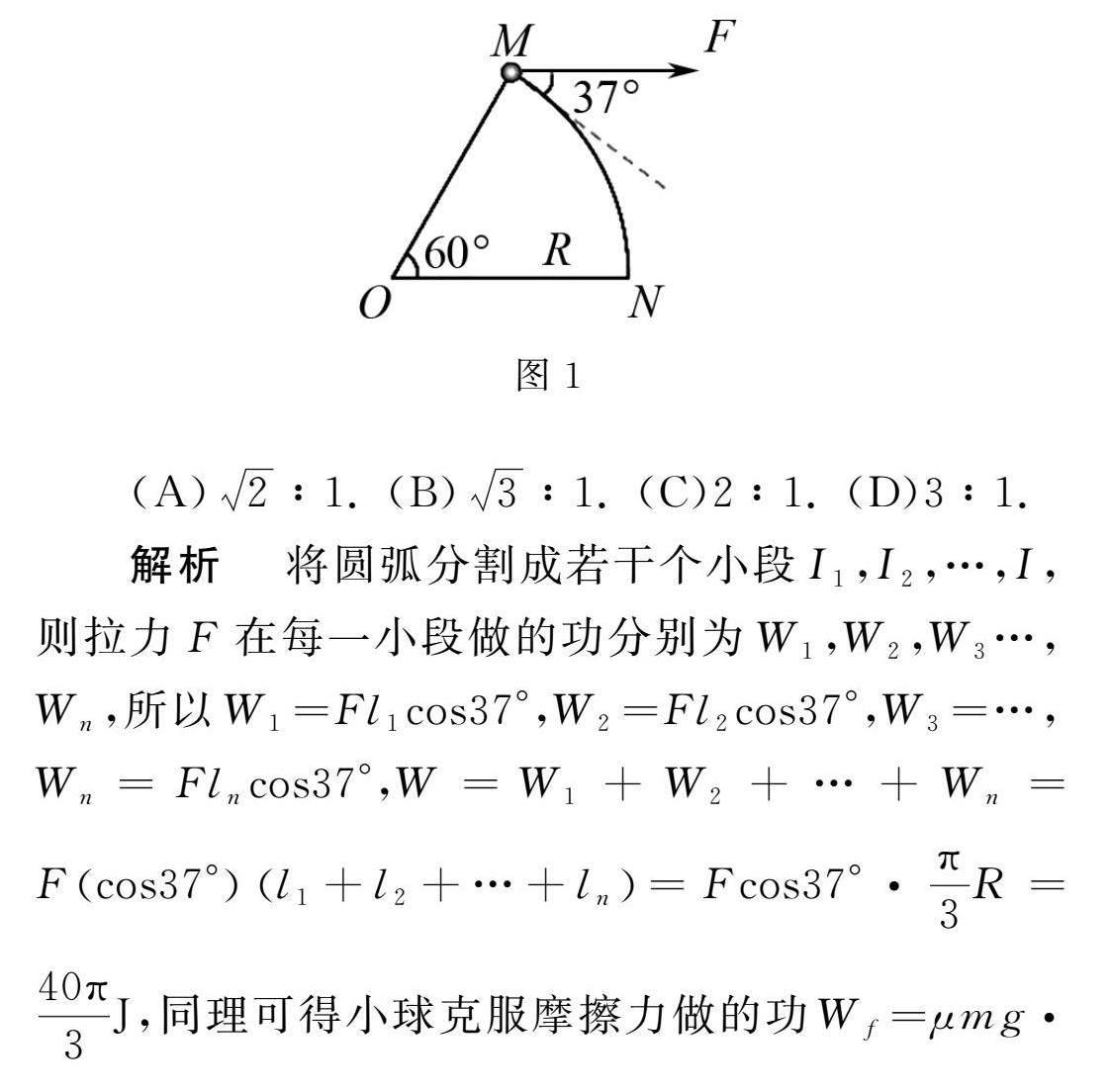
例1 水平桌面上，長R=5m的輕繩一端固定于O點(diǎn)，俯視圖如圖1所示，另一端系一質(zhì)量m=2.0kg的小球，現(xiàn)對小球施加一個(gè)F=10N的力，F(xiàn)拉著物體從M點(diǎn)運(yùn)動(dòng)到N點(diǎn)，方向始終與小球的運(yùn)動(dòng)方向成37°角.已知小球與桌面間的動(dòng)摩擦因數(shù)μ=0.2，不計(jì)空氣阻力，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8，則拉力F做的功與克服摩擦力做的功之比為（ ?）

（A）2∶1. （B）3∶1. （C）2∶1. （D）3∶1.

解析 將圓弧分割成若干個(gè)小段I1，I2，…，I，則拉力F在每一小段做的功分別為W1，W2，W3…，Wn，

所以W1=Fl1cos37°，W2=Fl2cos37°，W3=…，Wn=Flncos37°，W=W1+W2+…+Wn=Fcos37°l1+l2+…+ln=Fcos37°·π3R=40π3J，同理可得小球克服摩擦力做的功Wf=μmg·π3R=20π3J，拉力F做的功與小球克服摩擦力做的功之比為2∶1.故選（C）.

點(diǎn)評 力的大小不變，方向與運(yùn)動(dòng)方向相同，如果將小球運(yùn)動(dòng)的軌跡分成若干個(gè)微小段，力在每一微小段上可近似看成恒力做功，由于功是標(biāo)量，所以力在全過程中做的總功可用各微小段的功之和來計(jì)算.

2 微元法在解決空間電場問題中的應(yīng)用

例2 如圖2所示，兩個(gè)固定的半徑均為r的細(xì)圓環(huán)同軸放置，O1，O2分別為兩細(xì)圓環(huán)的圓心，且O1O2=2r，兩環(huán)分別帶有均勻分布的等量異種電荷+Q，－Q（Q>0）.一不計(jì)重力的帶正電的粒子從O1處由靜止釋放，靜電力常量為k，下列選項(xiàng)正確的是（ ?）

（A）粒子在O2處動(dòng)能最大.

（B）粒子在O1O2中點(diǎn)處動(dòng)能最大.

（C）O1O2中點(diǎn)處的電場強(qiáng)度為2kQr2.

（D）O1O2中點(diǎn)處的電場強(qiáng)度為2kQ2r2.

解析 根據(jù)電場疊加原理，在O2左側(cè)場強(qiáng)方向先向左后向右，因此粒子到達(dá)O2左側(cè)某一點(diǎn)時(shí)，速度最大，動(dòng)能最大，以后向左運(yùn)動(dòng)速度開始減小，動(dòng)能也在減小，故（A）錯(cuò)誤；帶電粒子從O1點(diǎn)開始由靜止釋放，在粒子從O1向O2運(yùn)動(dòng)的過程中，兩圓環(huán)對粒子的作用力都向左，可見電場對帶電粒子做正功.故粒子在O1O2中點(diǎn)處動(dòng)能不是最大，故（B）錯(cuò)誤；把圓環(huán)上每一個(gè)點(diǎn)都看成一個(gè)點(diǎn)電荷，則電荷量為q=Q2πr，根據(jù)點(diǎn)電荷場強(qiáng)公式，各點(diǎn)電荷在O1O2中點(diǎn)處產(chǎn)生的場強(qiáng)大小E=kq2r2，根據(jù)電場的疊加原理，單個(gè)圓環(huán)在O1O2中點(diǎn)的場強(qiáng)為E=kQ2r2cos45°，兩個(gè)圓環(huán)的場強(qiáng)，再疊加一下，有E總=2kQ2r2，故（C）錯(cuò)誤，（D）正確.

點(diǎn)評 高中階段的學(xué)生對點(diǎn)電荷周圍空間的電場分布比較熟悉，對均勻帶電圓環(huán)周圍空間電場的分布還比較陌生，如果將圓環(huán)分割成無限個(gè)小微元，每一個(gè)小微元就可看成一個(gè)點(diǎn)電荷，然后根據(jù)場強(qiáng)的疊加原理求解電場強(qiáng)度.

3 微元法求解導(dǎo)體棒切割磁感線的運(yùn)動(dòng)問題

例3 ?如圖3所示，兩根電阻不計(jì)的足夠長的平行金屬導(dǎo)軌MN和PQ放在水平面上，兩導(dǎo)軌的間距為L，左端連接有阻值為R的電阻.兩導(dǎo)軌處于豎直向上的磁感應(yīng)強(qiáng)度為B的勻強(qiáng)磁場中.現(xiàn)有一質(zhì)量為m、阻值為r的金屬棒放置在水平導(dǎo)軌上，給金屬棒一個(gè)瞬時(shí)沖量，使它獲得一個(gè)水平向右的初速度v0后開始沿導(dǎo)軌向右運(yùn)動(dòng).金屬棒運(yùn)動(dòng)過程中始終與導(dǎo)軌垂直且接觸良好，不計(jì)一切摩擦.

（1）金屬棒的速度為v時(shí)受到的安培力是多大？

（2）金屬棒向右運(yùn)動(dòng)的最大距離是多少？

解析 （1）當(dāng)金屬棒在磁場中運(yùn)動(dòng)到某一位置時(shí)的速度為v時(shí)，此時(shí)回路中的感應(yīng)電動(dòng)勢為E=BLv，

回路中的電流為I=ER+r，

金屬棒所受的安培力F安=BIL，

得F安=B2L2vR+r.

（2）金屬棒從速度為v0至停下來的過程中，由動(dòng)量定理得I安=0－mv0.

將整個(gè)運(yùn)動(dòng)過程劃分成很多小段，可認(rèn)為每個(gè)小段中的速度幾乎不變，設(shè)每小段的時(shí)間為Δt，則安培力的沖量

I安=－B2L2R+rv1·Δt+B2L2R+rv2·Δt+B2L2R+rv3·

Δt+…，

I安=－B2L2R+rv1·Δt+v2·Δt+v3·Δt+…，

I安=－B2L2R+rx，

解得x=mv0R+rB2L2.

點(diǎn)評 因金屬棒在運(yùn)動(dòng)的過程中，每個(gè)位置的速度大小均不相同，很難直接用動(dòng)量定理解答，如果將運(yùn)動(dòng)過程分割成若干個(gè)小段，在每一個(gè)小段上速度的大小可認(rèn)為不變，采用微元法解題.

4 結(jié)語

在高中物理解題中，一些比較復(fù)雜的物理過程表面上看起來無法解答，但稍加分析就可用已學(xué)過的熟悉的物理規(guī)律來解決，將復(fù)雜的問題簡單化.在使用微元法處理物理問題時(shí)，需將其分解為若干個(gè)微小的“微過程”，每個(gè)“微過程”所遵循的規(guī)律相同，這樣只需分析這些“微元過程”，然后將“微元過程”用數(shù)學(xué)手段或物理思想進(jìn)行處理，是一種“化整為零”再“集零為整”的思維方法，學(xué)生掌握了這種方法，有助于深度理解物理概念，拓展了解決物理問題的思路．

參考文獻(xiàn)：

[1]劉輝芳.微元法在高中物理教學(xué)中的應(yīng)用[J].中學(xué)物理教學(xué)參考，2023，52（12）：14-16.

[2]臧凱泉.微元法在高中物理解題中的有效應(yīng)用研究[J].數(shù)理化解題研究，2022（21）：70-72.

[3]裴加旺，劉蕊.微元法在高中物理教學(xué)中的應(yīng)用[J].物理之友，2022，38（02）：37-40.

[4]鄭成榮.“微元法”在高中物理解題中的應(yīng)用[J].中學(xué)物理教學(xué)參考，2020，49（12）：75.

[5]張海軍，唐安全.微元法在高中物理解題中的應(yīng)用探究[J].中學(xué)生理科應(yīng)試，2019（08）：21-23.