淺析小學(xué)數(shù)學(xué)教學(xué)中學(xué)生理性思維的培養(yǎng)

李林

【摘要】理性思維是人類思維的高級形式。《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》中指出，學(xué)生要能運用數(shù)學(xué)的思維方式進(jìn)行思考。本文結(jié)合教學(xué)實踐，在觀察比較中激發(fā)理性思維介入，在分析說理中引導(dǎo)理性思維發(fā)展，在抽象概括中助推理性思維深入。

【關(guān)鍵詞】理性思維；小學(xué)數(shù)學(xué)；運算律

理性思維是人類思維的高級形式，它能夠加深學(xué)生對所學(xué)知識的理解，讓學(xué)生擁有更嚴(yán)謹(jǐn)?shù)慕鉀Q問題的方法和態(tài)度。《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》指出：“通過義務(wù)教育階段的數(shù)學(xué)學(xué)習(xí)，學(xué)生能……運用數(shù)學(xué)的思維方式進(jìn)行思考……”如何在小學(xué)數(shù)學(xué)課堂教學(xué)中培養(yǎng)學(xué)生的數(shù)學(xué)理性思維呢？筆者以“運算律”相關(guān)內(nèi)容的教學(xué)為例談?wù)剬@個問題的一些體會。

運算律是對一些相似運算現(xiàn)象進(jìn)行觀察、比較、分析而抽象概括出來的規(guī)律。不難發(fā)現(xiàn)，運算律的探究過程正是理性思維的發(fā)生過程。因此組織學(xué)生探索和發(fā)現(xiàn)運算規(guī)律不單單是獲取知識，這一過程還有助于培養(yǎng)學(xué)生的理性思維。

一、在觀察比較中激發(fā)理性思維介入

小學(xué)生的年齡特點決定了他們學(xué)習(xí)新知識時，感性思維仍占主導(dǎo)地位。課堂教學(xué)的導(dǎo)入環(huán)節(jié)，教師給出感性素材引導(dǎo)學(xué)生觀察比較、主動思考，激發(fā)理性思維介入，引導(dǎo)他們透過現(xiàn)象發(fā)現(xiàn)規(guī)律，從而發(fā)展學(xué)生的理性思維。

例如在學(xué)習(xí)“加法交換律”時，教師可以先請男女生進(jìn)行分組口算，口算題設(shè)計為：男8+9，女9+8；男46+5，女5+46；男20+162，女162+20……活動中男生說左右兩個算式得數(shù)相等，比賽不公平，教師可以追問：“怎么答案就相等了呢？”學(xué)生的目光一下就聚焦到了本課要研究的內(nèi)容上來：兩個加數(shù)交換位置，和不變。在學(xué)生發(fā)現(xiàn)算式特征后，繼續(xù)要求：“再算一算，是不是真相等？”引導(dǎo)學(xué)生通過計算再次確認(rèn)，并順勢將對應(yīng)的兩個算式寫成等式的形式。緊接著用“你還能舉幾個例子嗎？”“觀察這些等式，你有什么發(fā)現(xiàn)？”等問題有效引導(dǎo)學(xué)生借助有形的等式，將感性認(rèn)識上升為理性認(rèn)識，從而提煉出數(shù)學(xué)規(guī)律，這正是學(xué)生發(fā)展理性思維的開端。

二、在分析說理中引導(dǎo)理性思維發(fā)展

數(shù)學(xué)是一門邏輯嚴(yán)密的學(xué)科，對于數(shù)學(xué)知識的分析說理要培養(yǎng)學(xué)生“知其然，更知其所以然”的理性意識，使學(xué)生對知識的理解不再停留在表面層次，而是更加深刻和理性。

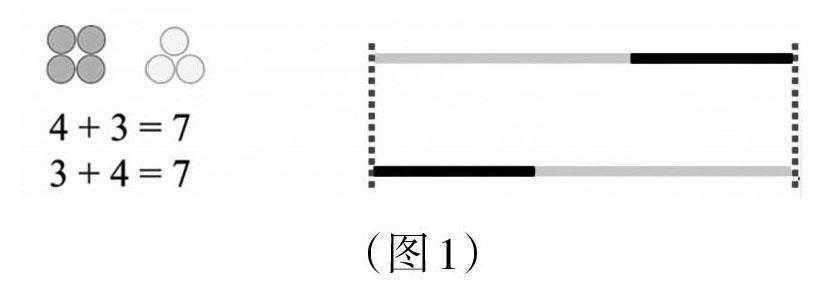
比如在教學(xué)“加法交換律”時，教師可逐步出示圖片（圖1），引導(dǎo)學(xué)生思考：“兩個加數(shù)交換位置，和不變，到底是什么道理呢？”接下來學(xué)生借助數(shù)形結(jié)合的方法，逐步認(rèn)識到“兩個數(shù)相加，無論怎么交換位置，結(jié)果都是把這兩個數(shù)合起來，所以和一定不變”。在整個分析、說理的過程中，學(xué)生的理性思維得到了發(fā)展。

對事物本質(zhì)的認(rèn)識，是理性思維的核心。從生活化的情境到數(shù)學(xué)化的過程，是學(xué)生數(shù)學(xué)學(xué)習(xí)的重要過程，也是數(shù)學(xué)理性發(fā)展的重要邏輯。學(xué)數(shù)學(xué)不能停留在知道“是什么”，還要明白“為什么”。教師教學(xué)時應(yīng)努力讓學(xué)生在發(fā)現(xiàn)規(guī)律的基礎(chǔ)上尋求“合情合理”的解釋說明，發(fā)展學(xué)生的數(shù)學(xué)思維。

三、在抽象概括中助推理性思維深入

“關(guān)系”是數(shù)學(xué)的核心，數(shù)學(xué)理性思維重要表現(xiàn)之一就是思維的整體性、結(jié)構(gòu)性。培養(yǎng)學(xué)生理性思維的一個重要途徑，就是培養(yǎng)學(xué)生的模型思想，也就是抽象概括能力。課堂教學(xué)中教師需要讓學(xué)生經(jīng)歷“數(shù)學(xué)化”和“再創(chuàng)造”的過程，去掉數(shù)學(xué)問題中非本質(zhì)的東西，用數(shù)學(xué)語言或數(shù)學(xué)符號進(jìn)行表述，提煉出數(shù)學(xué)模型。

“運算律”教學(xué)時從一開始的若干個等式出發(fā)，到用文字來描述等式所體現(xiàn)的規(guī)律，再到用多種方式去驗證猜想并得出結(jié)論，最后提出用更簡潔的方式來表示這一規(guī)律，學(xué)生很快想到用圖形和符號來表示：“△+○=○+△”“a×（b+c）=a×b+a×c”。教師進(jìn)一步引導(dǎo)學(xué)生深入思考：這字母表示的數(shù)可以是什么數(shù)？看著字母表達(dá)式，什么變了？什么不變？結(jié)果不變的關(guān)鍵是什么？學(xué)生在追求簡約化的數(shù)學(xué)學(xué)習(xí)中進(jìn)行抽象概括，感受到符號化的精髓，也達(dá)成了對知識本質(zhì)的認(rèn)識，這便是理性思維深入的體現(xiàn)。

數(shù)學(xué)學(xué)習(xí)，既要注重知識的“生長點”，也要關(guān)注思維的“鏈接點”。學(xué)生一步步地把對運算中的規(guī)律的認(rèn)識從感性上升到理性的層次，從宏觀角度進(jìn)行分析、思考，不僅僅總結(jié)發(fā)現(xiàn)了運算規(guī)律，更從理性的數(shù)學(xué)角度理解它成立的意義。學(xué)生所經(jīng)歷的不僅是一種數(shù)學(xué)知識的收獲過程，更為重要的是從中獲取一種理性的思維方式：觀察、分析、歸納、抽象和概括，同時也培養(yǎng)了嚴(yán)謹(jǐn)求實、勇于探索的理性精神。

在教育“生本”化的今天，要讓學(xué)生自己主動地學(xué)習(xí)，讓學(xué)生的思維進(jìn)行碰撞，使學(xué)生得到全面發(fā)展。

（作者單位：江蘇省南京市金陵中學(xué)河西分校）