基于改進灰狼優化算法的含光伏配電網動態無功優化

于惠鈞 馬凡爍 陳 剛 楊馳澤 李嘉軒

基于改進灰狼優化算法的含光伏配電網動態無功優化

于惠鈞 馬凡爍 陳 剛 楊馳澤 李嘉軒

（湖南工業大學電氣與信息工程學院，湖南 株洲 412007）

針對光伏并網對配電網造成的電壓波動、線損增加，以及光伏和負荷出力的不確定性等問題，本文構建基于二階錐規劃的線性凸優化模型，通過控制有載調壓變壓器和電容器組動作，以及光伏逆變器和靜止無功發生器無功補償能力約束，對日前日內雙時間尺度無功優化模型進行動態分析，在簡化求解過程的同時加大找到全局最優解的可能性。提出一種基于混沌學習初始化、非線性收斂因子、最優粒子柯西擾動結合蜘蛛猴算法位置更新方式的改進灰狼優化算法，防止算法陷入局部最優并增強其全局搜索能力。最后，運用改進的灰狼優化算法對含光伏的IEEE 33節點系統進行建模仿真，結果表明該算法具有尋優效率高、收斂速度快的優點，驗證了算法的可行性和高效性。

配電網；光伏發電；動態無功優化；二階錐規劃；灰狼優化算法（GWO）

0 引言

新能源發電設備的大規模持續并網是當下我國電網的重要發展趨勢，在傳統電網格局和電源結構不斷更替的背景下，電力系統安全穩定運行狀態也發生了深刻變化[1]。分布式光伏在接入配電網時，光伏出力的不確定性不僅會增加系統網絡損耗和電壓越限風險，還會導致配電網無功優化模型呈現非凸特性[2-3]。為了保證電能質量、降低系統網損[4]，需要通過電容器組、有載調壓變壓器（on-load tap changer, OLTC）等傳統調壓裝置或光伏并網逆變器與靜止無功發生器（static var generator, SVG）等無功補償裝置進行調節[5]。

針對光伏配電網眾多調節設備的協調優化問題，文獻[6]提出一種混合時間尺度下的無功/電壓控制策略，在日前尺度綜合考慮OLTC和電容器組動作以降低離散調壓設備動作次數，在實時尺度修正光伏逆變器無功出力。在光伏逆變器控制策略方面，文獻[7]提出一種可靠性約束配電網中的電壓/無功控制（volt/var control, VVC）優化模型，旨在同時最小化電網功率損耗和光棄用功率。在建立考慮光伏電源可靠性的配電網無功優化模型過程中，需要對不同類型的控制設備采取不同的控制策略，從而進一步減小電壓偏差和網絡損耗[8-10]。

對于光伏接入的配電網無功優化問題，以運用智能算法求解最為廣泛[11]。文獻[12]提出一種基于合作優化算法（cooperation search algorithm, CSA）的含光伏配電網有功無功協調優化模型，通過結合粒子群優化算法（particle swarm optimization, PSO）提高搜索效率，減小系統損耗。文獻[13]采用優質蝙蝠鄰域搜索對光伏接入的配電網進行無功優化，但未考慮光伏出力的隨機性。由于一天內的光照是隨時間波動的，因此光伏出力具有不確定性。文獻[14]在考慮光伏出力不確定性的前提下，采用混沌搜索改進粒子群算法，求解含高滲透率光伏配電網在長時間尺度下的無功優化方案，但未深入考慮如何在全局優化范圍內對離散設備動作次數進行限制。離散設備在相鄰時間尺度下的連續動作可能會對配電網造成沖擊，增加系統運行風險。研究表明，灰狼優化（gray wolf optimization, GWO）算法比PSO具有更好的收斂性和求解精度[15]。文獻[16]在混沌搜索的基礎上通過反向學習策略對GWO進行改進，有效避免了求解陷入局部最優。文獻[17]采用反向學習混沌種群初始化，并引入柯西變異來提高GWO的前期搜索能力。在構建目標函數方面，智能算法無需像傳統算法一樣確立明確的表達形式，只需輸入輸出即可。

本文在計及光伏和負荷波動性的前提下，通過二階錐規劃構建線性凸優化模型，在雙時間尺度下綜合考慮光伏配電網不同調壓裝置間的無功優化策略，引入電網安全性指標構建目標函數，對日前離散性設備動作設限并對SVG進行分時段調節；同時，提出一種動態自適應灰狼優化算法，結合蜘蛛猴算法（spider monkey optimization, SMO）進行個體位置更新，并對早熟粒子進行柯西擾動。利用IEEE 33節點系統對含光伏接入的配電網無功優化問題進行仿真求解，以驗證所提算法的有效性。

1 光伏出力的數學模型

配電網中接入分布式光伏后需要對無功功率進行調節。由于光伏及負荷出力的隨機性與波動性[18]，為了保證電容器組、有載調壓變壓器等離散型控制設備與光伏逆變器、SVG等連續型控制設備之間的協調配合，綜合考慮光伏出力預測誤差，以及資源的最佳利用，需要構造不同時間尺度下的調壓裝置控制策略。本文設計日前和日內雙時間尺度下的控制策略，并構建其數學優化模型。

1.1 日前無功優化模型

日前無功優化模型需要根據光伏出力曲線和負荷變化因子構建，將響應速度慢且動作次數受限的OLTC和電容器組作為離散型控制變量，確定一天24h的最優調節計劃。含OLTC的支路潮流模型如圖1所示，其中P+jQ為支路位于節點處的視在功率，P+jQ為支路位于節點處的視在功率，R+jX為支路的阻抗，K為OLTC的電壓比，P、Q分別為節點注入的有功功率、無功功率。

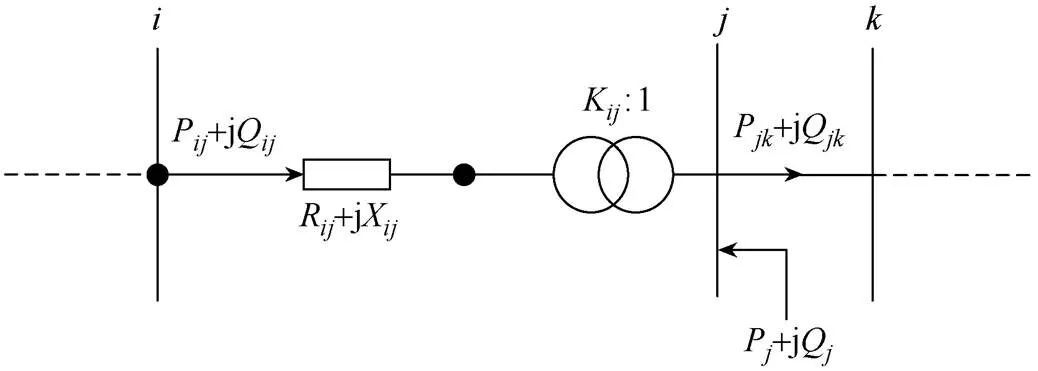
圖1 含OLTC的支路潮流模型

1）目標函數

（1）系統有功網損

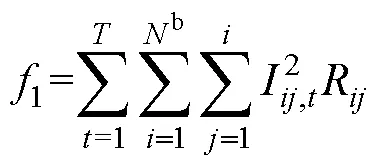
（2）節點電壓偏差

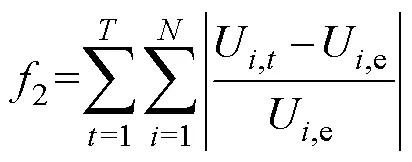
（3）電網安全指標

為了表示光伏接入電網側對電能質量的影響程度，本文提出電網安全指標以評估電網電能質量和抗風險能力，包括電壓脆弱度指標和電壓越限風險指標。

時刻節點的電壓脆弱度為

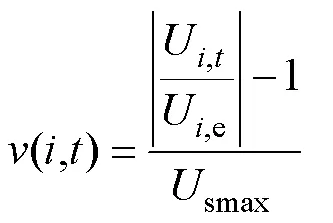
式中，smax為系統最大電壓偏差。

由式（3）斷面歸一化可得

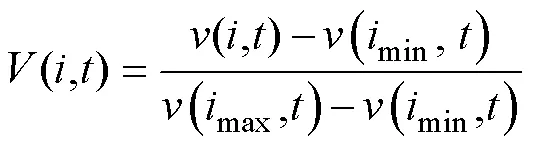
電網一日內的總脆弱度為

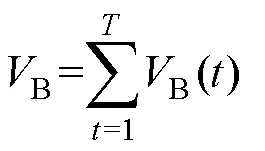
式中，B()為歸一化后電網在時刻的電壓脆弱度。

電壓越限指標采用風險偏好效用函數評估，有

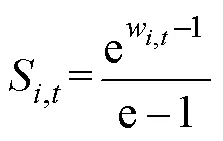
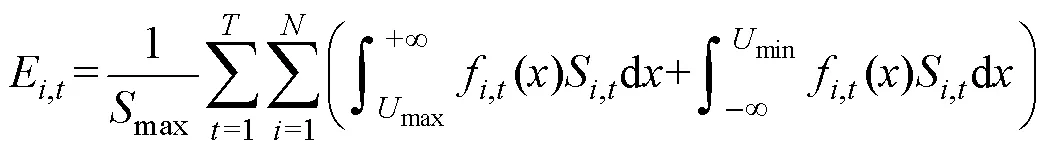
式中：max為電壓越限風險嚴重度的最大值；f,t()為時刻節點的電壓概率分布；max為系統電壓最大值；min為系統電壓最小值。

最后求得電網安全指標為

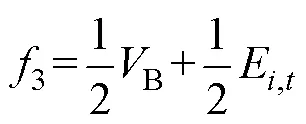
（4）多目標函數歸一化計算

在求解最優問題的過程中，會出現多個目標函數的優化，且這些目標函數間存在不兼容性。本文采取權重系數法進行歸一化處理，將多目標問題轉化為單目標問題求解，即

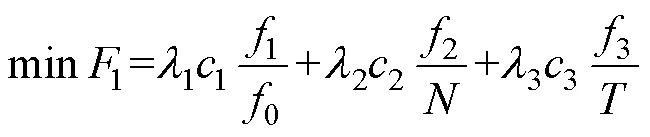
2）約束條件

（1）等式潮流約束

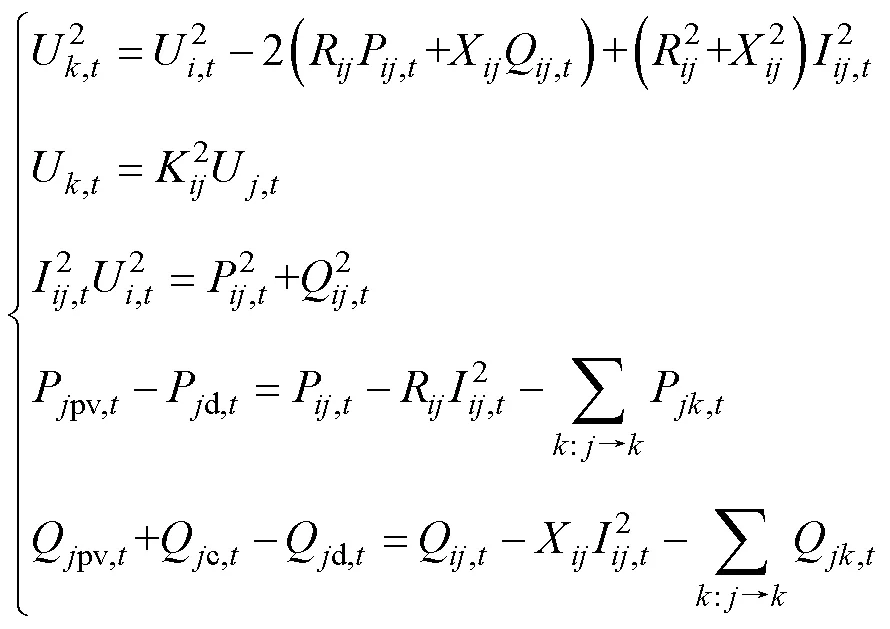
式中：P,t、Q,t為時刻節點和節點之間流通的有功功率和無功功率；Ppv,t、Pd,t和Qpv,t、Qc,t、Qd,t分別為節點在時刻的光伏有功出力、有功負荷和光伏無功出力、電容器無功補償和無功負荷；:→表示以為父節點的子節點集合。

（2）不等式約束

節點電壓約束為

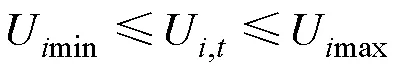
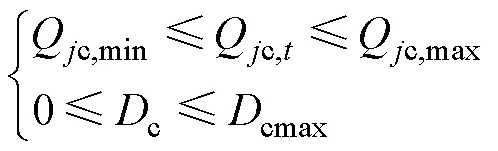
式中：Qc,min、Qc,max為電容器無功出力最小值、最大值；cmax為電容器投切次數最大值。

有載調壓變壓器約束為

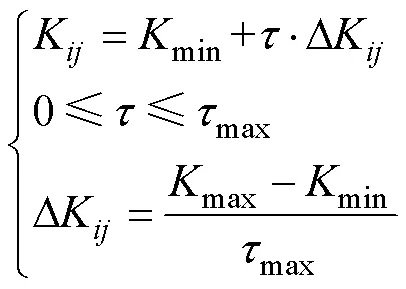
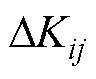
光伏有功功率與無功功率約束為

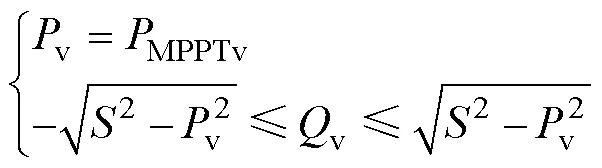
式中：v為光伏逆變器有功出力；MPPTv為光伏逆變器最大跟蹤點功率；v為光伏逆變器無功出力；為光伏逆變器視在容量。

離散設備相鄰時段投切約束為

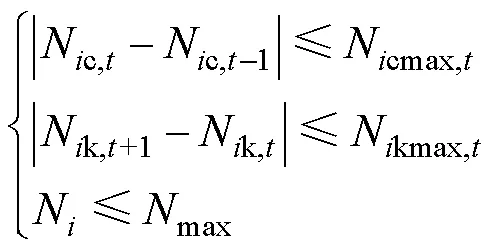
式中：Nc,t為時刻電容器的投切組數；Nk,t為時刻有載調壓變壓器分接頭擋位；N為離散設備連續動作次數；Ncmax,t為電容器在相鄰時段下的最大動作次數；Nkmax,t為變壓器在相鄰時段下的最大動作次數；max為離散設備允許連續動作的最大次數。

1.2 日內無功優化模型

日內無功優化需要對光伏的多運行狀態進行對應調整，同時將響應速度快且可連續調節的光伏逆變器組作為連續型控制變量對節點電壓進行優化，在日前離散設備計劃基礎上，以15min為間隔獲得光伏無功矯正值，以保證配電網運行的可靠性和經濟性。

1）光伏逆變器優化控制策略

光伏逆變器是可快速連續調節的配電網重要無功電源之一，通過并網完成電能質量的調節和無功補償。常用的光伏并網控制策略存在一定弊端，無法實現電壓與網損之間的協同配合。本文采用一種改進的電壓有功協調控制策略(,)，通過光伏出力的大小決定光伏逆變器的無功補償范圍，并根據電壓的不同水平決定光伏逆變器的無功補償措施。

改進(,)控制策略曲線如圖2所示，根據有功出力決定最大無功補償量max的取值范圍，當電壓小于0.98p.u.時，光伏逆變器發出無功功率，使電壓抬升，且隨有功出力的增加，max逐漸減小，從而避免無功過度補償；當電壓為0.98p.u.～1.02p.u.時，可以認為工作于理想電壓區域，此時max=0，無功功率不補償；當電壓大于1.02p.u.時，光伏逆變器吸收無功功率，且隨著有功出力的增加，max逐漸增大，使電壓有效降低，避免電壓越限。

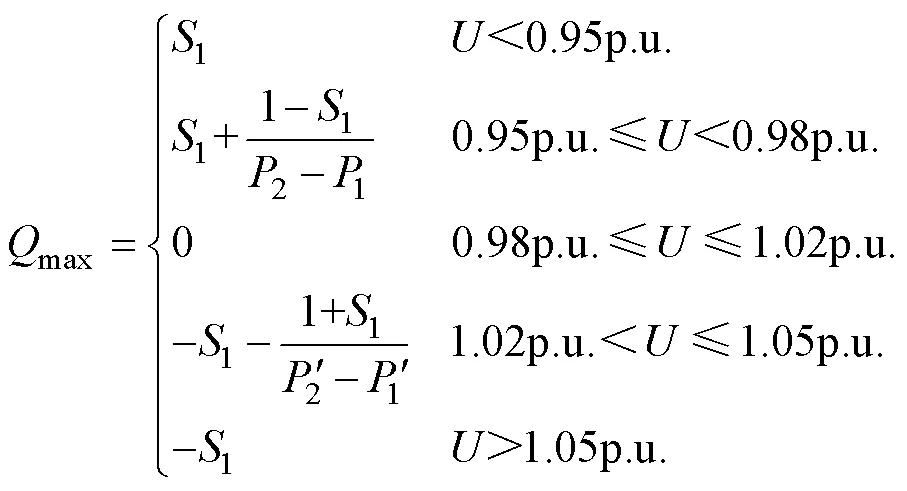
式中：S1為光伏逆變器無功補償最大值；U為系統電壓；、分別對應于系統電壓規定的上、下限；、分別對應于系統規定的理想電壓上、下限。

2）目標函數和約束條件

日內無功優化目標函數2主要考慮電壓偏差和電網安全兩個指標。

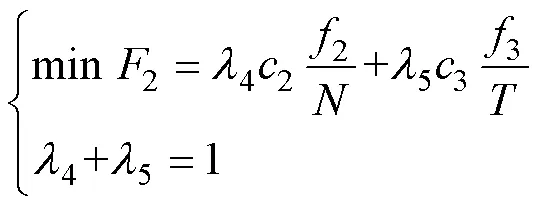
日內無功優化需要滿足的約束主要包括等式約束、節點電壓約束和光伏有功功率、無功功率約束。

1.3 基于二階錐規劃的無功優化模型

包含OLTC的支路潮流模型是非凸、非線性的，其確立的以有功網損為基準的目標函數和潮流約束包含二次項，使原模型的求解較困難且難以找到全局最優。為此，引入二階錐松弛和OLTC線性化，將其轉化為凸模型進行求解[19]，以在簡化模型求解的基礎上更好地找到全局最優。

1）二階錐松弛

在計算最優潮流過程中引入錐優化變量，即

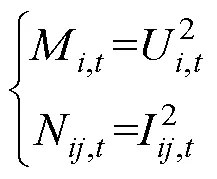
將式（18）代入1和支路潮流約束后有

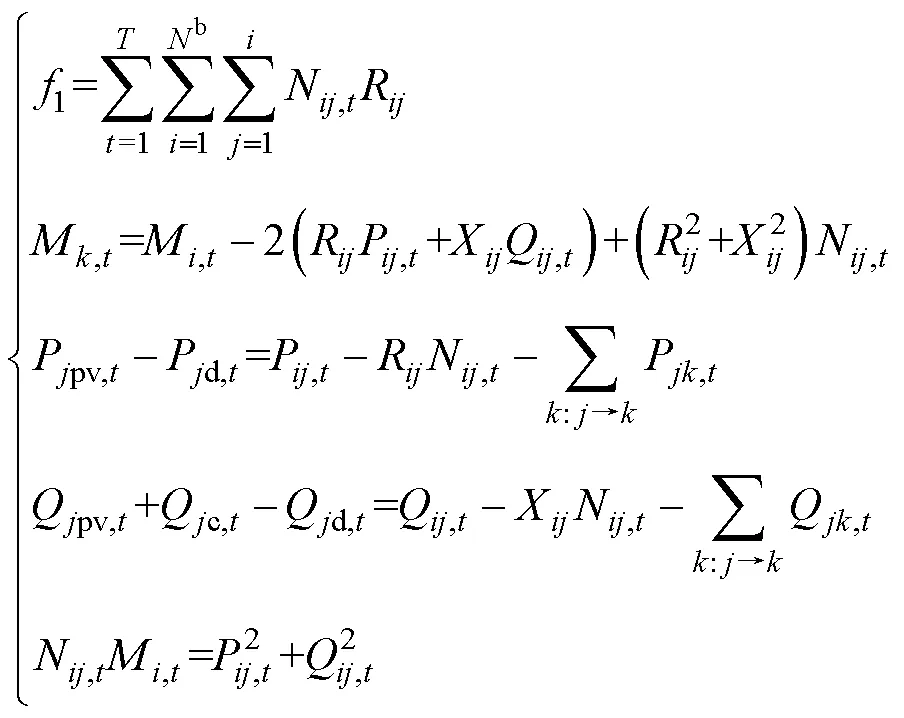
通過二階錐松弛可得約束為

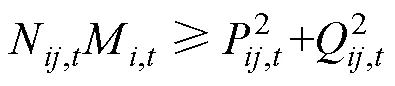
轉換為標準二階錐可得

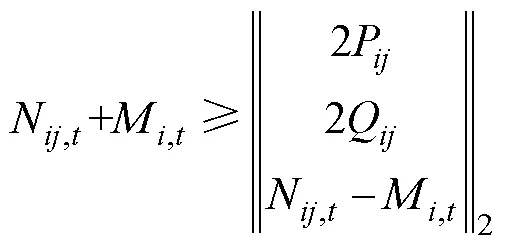
通過對算例結果進行檢驗可以確定此二階錐松弛準確。

2）OLTC線性處理

將變壓器約束通過二進制線性化處理轉化為凸約束，有

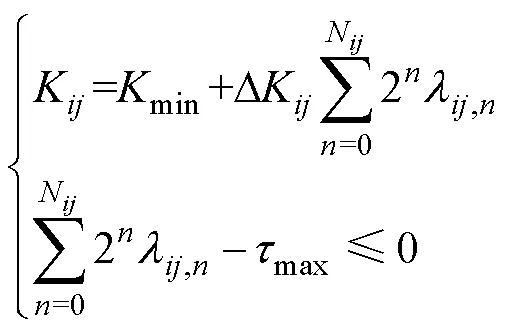
將式（22）通過大M法變換可得轉換后的凸約束為

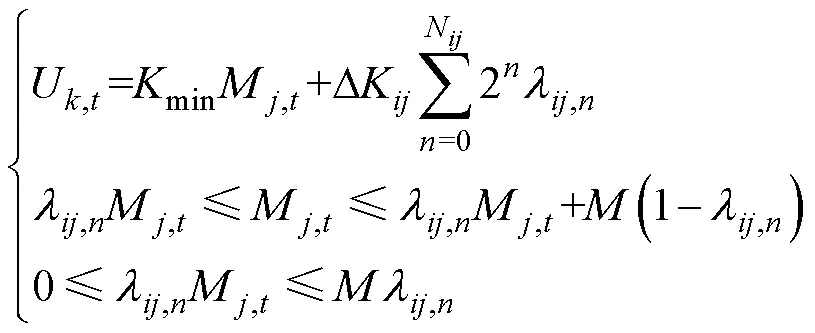
式中，為非無窮大正值變量，由約束條件極值決定。

綜上可得修正后的1、潮流約束及有載調壓變壓器約束。此時，所求無功優化模型已符合線性凸約束條件。

1.4 SVG分時段無功補償策略

通過改進后的光伏逆變器控制策略可以有效降低電壓越限風險，同時針對不同情況靈活進行無功補償。但由于光照強度直接決定光伏逆變器的輸出功率，當光照較弱時，光伏逆變器的補償效果并不能達到理想預期。尤其是在夜晚無光時段光伏出力為0，此時光伏并網點只存在就地負荷，單純依靠光伏逆變器無法實現無功補償控制。本文采用一種基于SVG的分時段無功補償策略，利用其既可吸收又可發出無功功率的能力，在光伏出力達到預期值時關斷，在光伏出力低于預期值時加入，通過可關斷開關元件在指定時段區間發出電壓相位幅值，進行動態無功補償，并保證投資運行的經濟性。SVG動態無功調節模型可表示為

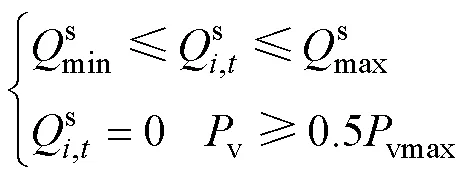
2 基于改進灰狼優化算法的無功優化

2.1 標準灰狼優化算法

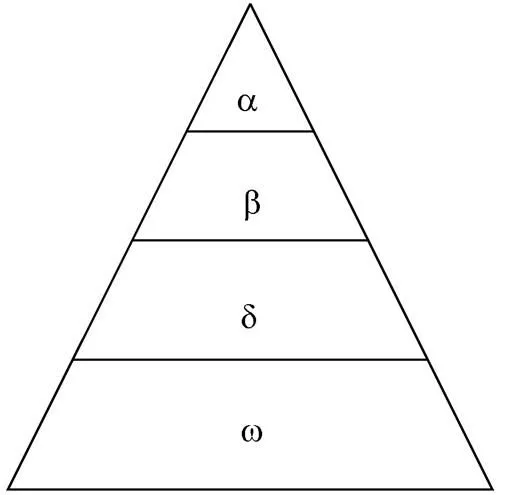
圖3 灰狼等級制度

1）包圍獵物

灰狼群體在找尋獵物時會逐步形成包圍圈，將這種行為定義為

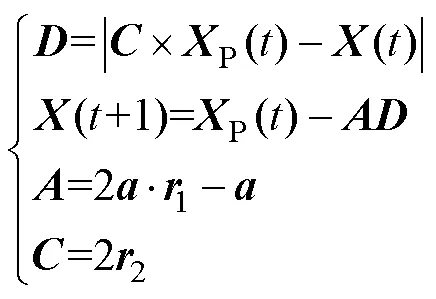
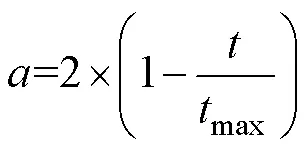
式中：為距離向量；、為行為系數；為當前迭代次數；P為獵物的位置向量；()為迭代次后的灰狼位置向量；為收斂因子；1、2為[0, 1]之間的隨機數向量；max為種群最大迭代次數。

2）捕食獵物

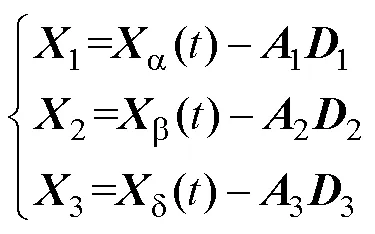
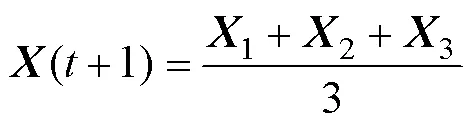
2.2 改進灰狼優化算法

1）Tent映射透鏡學習種群初始化

標準灰狼優化算法的初始種群是隨機產生的，在空間中的分布并不均勻，容易造成局部最優。為了使隨機產生的個體盡可能在整個空間分布，本文對初始化種群采用Tent混沌映射以增強種群在整個空間中的分布能力。

透鏡學習以反向學習策略為基礎，對其相反問題進行建模求解，可以提高算法的魯棒性。將Tent映射與透鏡學習機制相結合應用于種群初始化，有

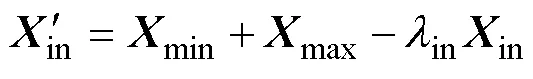
2）基于指數函數的非線性收斂因子

由于GWO算法中的收斂因子隨迭代次數的增加而線性減小，在算法后期不能兼顧全局與局部搜索能力，可能會導致局部最優。本文引進指數函數對收斂因子進行改進，即

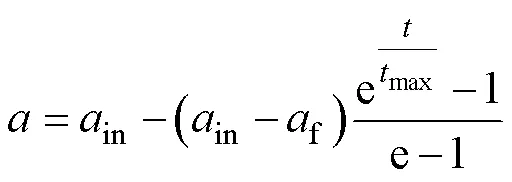
式中，ain和af分別為a的初始值和最終值。所得到的非線性收斂因子隨迭代次數的變化曲線如圖4所示。

由圖4可得，改進后的收斂因子減小較慢，能更好地適應全局搜索，在迭代后期也能提高算法的局部搜索能力。

3）動態自適應個體位置更新

受蜘蛛猴算法啟發，通過使用全局領導者和本地領導者的組合信息來更新個體位置。在進行無功優化的過程中，需要對網損最低和電壓偏差最小節點等進行深度挖掘，因此本文增加線性遞減慣性權重，使其在迭代前期獲得較大值并隨迭代次數的增加而逐漸遞減，在保證全局搜索能力的同時提升算法后期的局部搜索能力，既可避免前期陷入局部最優，又可保證后期不跳出局部最佳點。

狼群位置更新為

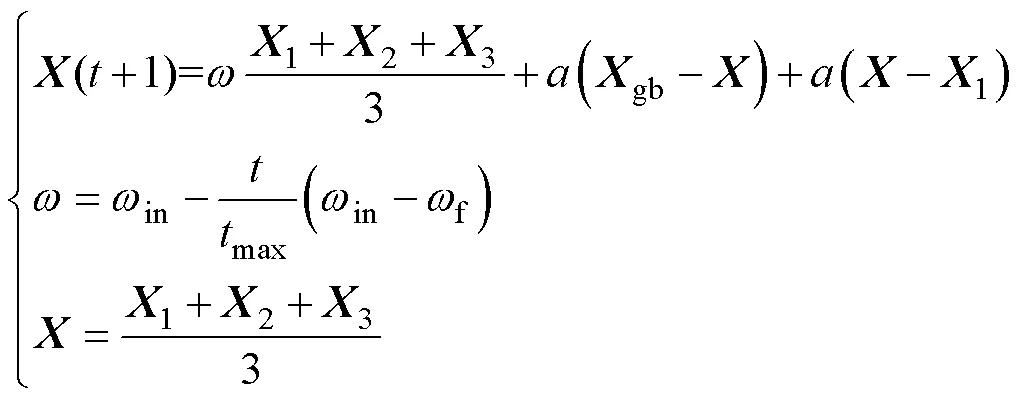
4）柯西變異

算法迭代后期粒子會表現出強烈的趨同性，易陷入早熟收斂，本文引入聚集度函數來判斷粒子是否陷入早熟收斂狀態并對陷入粒子進行排序，對排名前25%的粒子進行柯西擾動來提升全局搜索能力。

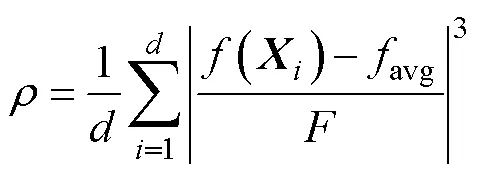
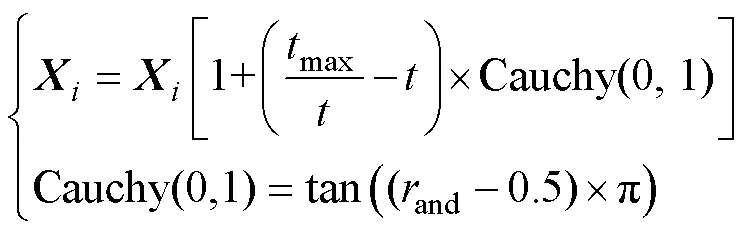
式中：Cauchy(0, 1)為標準的柯西擾動隨機值；and為[0, 1]之間均勻分布的偽隨機數。

2.3 改進灰狼優化算法流程

改進灰狼優化算法的流程如圖5所示。

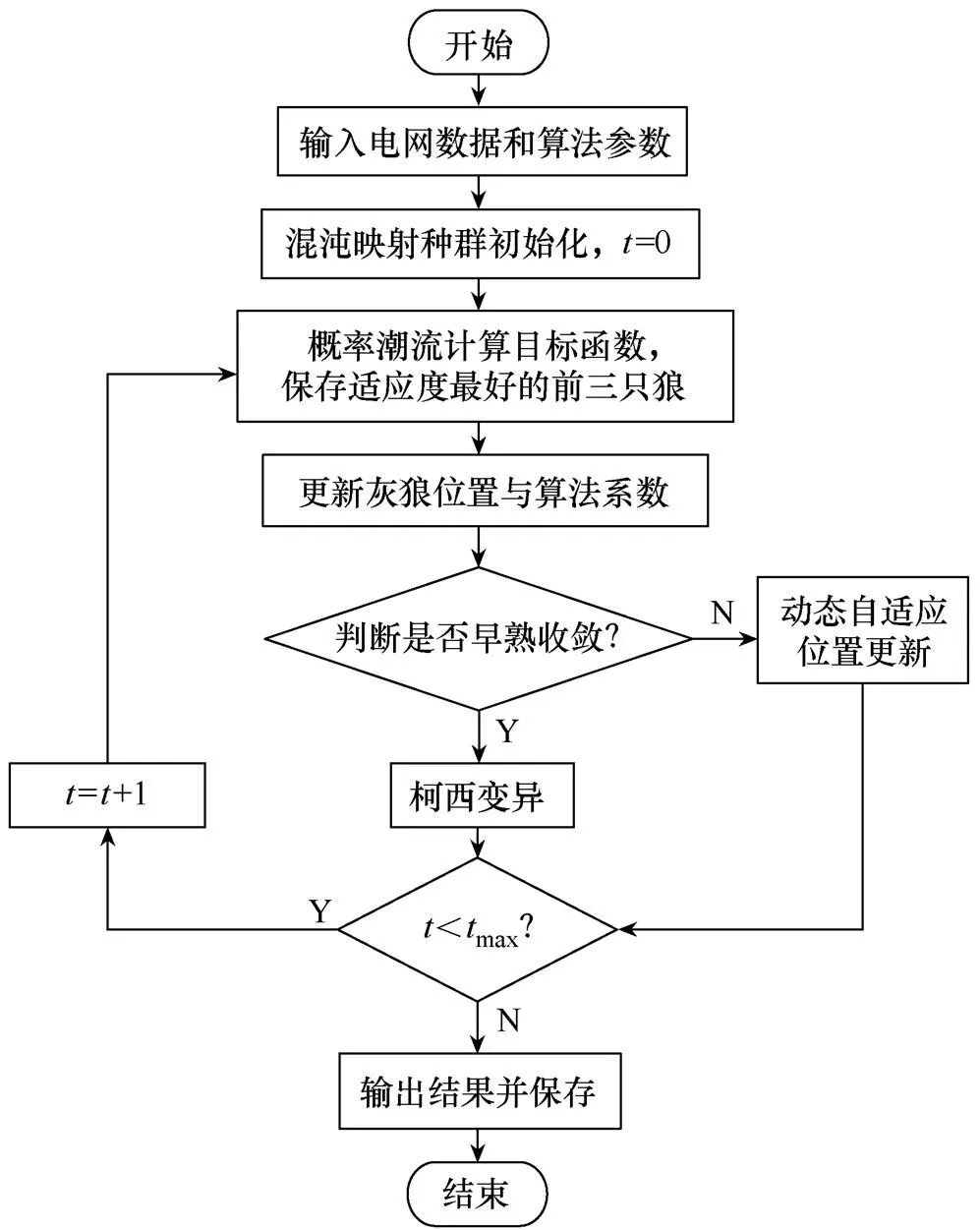
圖5 改進灰狼優化算法流程

在日前時間尺度輸入配電網參數、24h光伏及負荷出力預測值，并建立優化模型各約束程序模塊后，對離散型設備動作次數設限，建立日前計劃模型，通過改進灰狼優化算法進行動態無功優化得到未來24h配電網無功出力計劃；在日內時間尺度輸入配電網參數、未來15min光伏及負荷出力預測值，在日前計劃得到母線電壓參考值和離散設備動作計劃的基礎上優化配電網電壓分布，以節點電壓偏差最小為目標得到未來15min內的光伏出力及SVG修正值。

3 算例分析

3.1 基本參數設置

改進IEEE 33節點系統結構如圖6所示，系統基準電壓B=12.66kV，系統基準功率B=10MV?A。在節點15、21、33接入光伏，光伏陣列的面積8 000m2，光電轉換效率0.2；光伏逆變器容量1 800kV?A；在節點9和節點24接入SVG補償裝置，補償容量為1MV?A；在節點18、30分別接入10組、20組電容器，單組容量50kV?A；有載調壓變壓器電壓比范圍0.9～1.1，可調節擋位共9擋。光伏逆變器功率因數[0.95, 1.05]；節點電壓約束[0.95p.u., 1.05p.u.]。設置離散設備日最大動作次數8次，相鄰時段動作限制3次，連續動作最大次數限制3次。

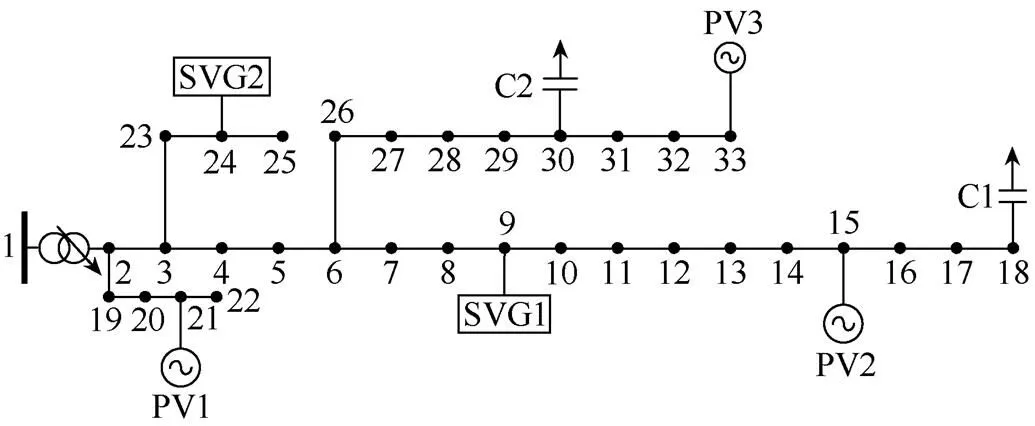
圖6 改進IEEE 33節點系統結構

算法參數設置：種群規模設置為50，最大迭代次數100次，收斂因子in=2，f=0；慣性權重in=0.9，f=0.4。

3.2 改進灰狼優化算法無功優化分析

在對接入光伏后的配電網進行分析的過程中，一天內的光照強度和負荷波動是不確定的，通過輸入的網絡參數和24h負荷與光伏出力曲線可以得到日前計劃，并通過對離散型設備進行動作約束減小投切過程對配電網造成的沖擊。以日前離散設備的動作計劃為基礎，可以得到未來15min內的光伏逆變器無功出力。通過日前計劃得到的OLTC及電容器組投切計劃分別如圖7～圖9所示。

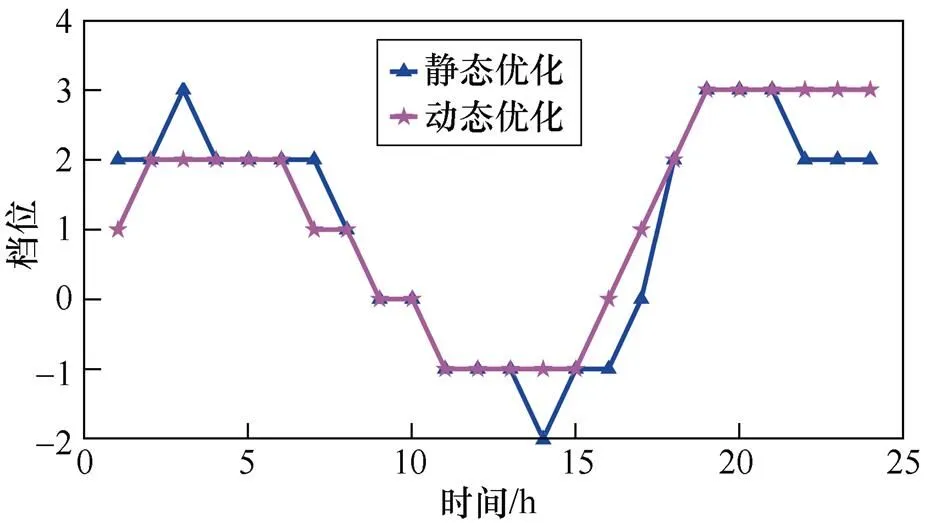
圖7 OLTC投切擋位

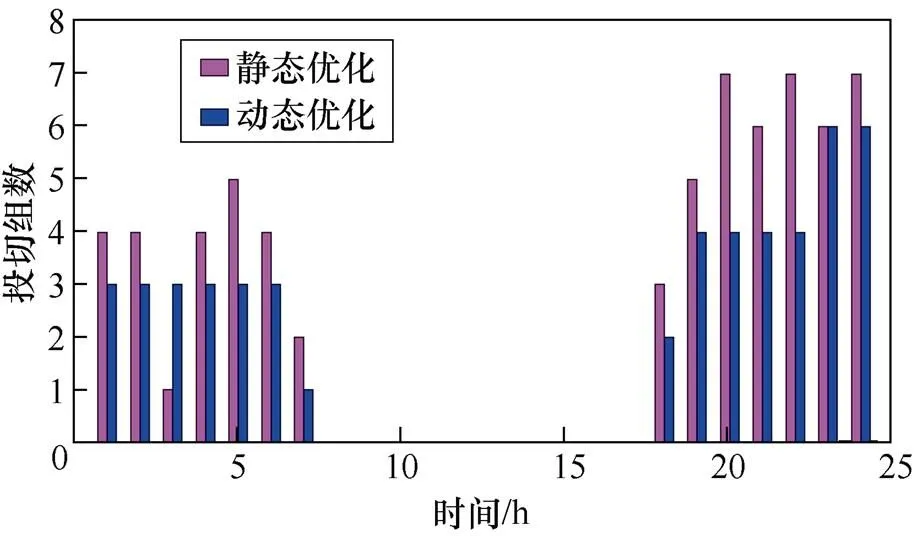
圖8 C1投切組數

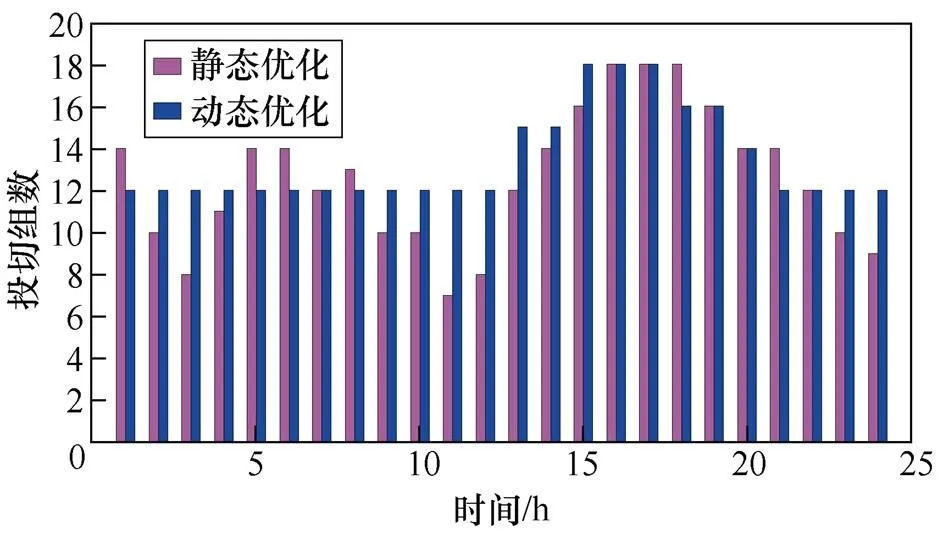
圖9 C2投切組數

由圖7～圖9可知，靜態方法下的OLTC動作次數為11次，C1動作次數13次，C2動作次數18次。而采用動態優化方法后的OLTC動作次數為8次，C1、C2動作次數均為5次，較少的動作次數可以延長設備使用壽命，同時避免離散設備投切時幅度過大。通過日內計劃得到的光伏逆變器無功出力比如圖10所示。

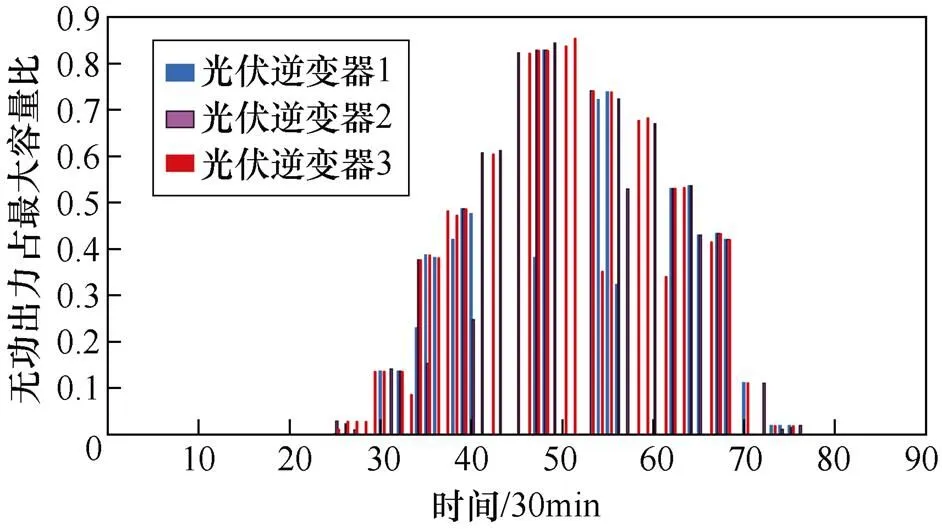
圖10 光伏逆變器無功出力比

在得到日前和日內投切計劃后，為了驗證改進灰狼優化算法的收斂性，將其與PSO、GWO和未結合蜘蛛猴算法的改進灰狼優化算法進行比較，通過迭代100次后對所得結果求平均值得到不同算法的迭代曲線如圖11所示。

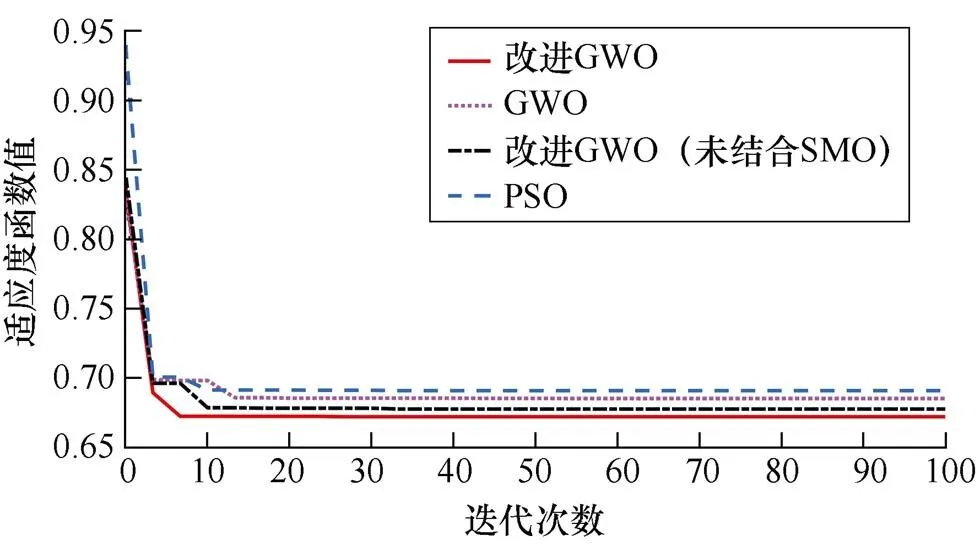
圖11 不同算法的迭代曲線

通過對不同算法迭代曲線的比較可以發現，改進灰狼優化算法在找到最優解時所需要的迭代次數更少，可以更快找尋到全局最優。同時，在算法精度方面收斂性更強，所得到的適應度函數值更小，尋優效率更高。

對光伏接入配電網后的24h系統各節點電壓求平均值后，得到的IEEE 33節點系統優化前后的節點電壓曲線如圖12所示。

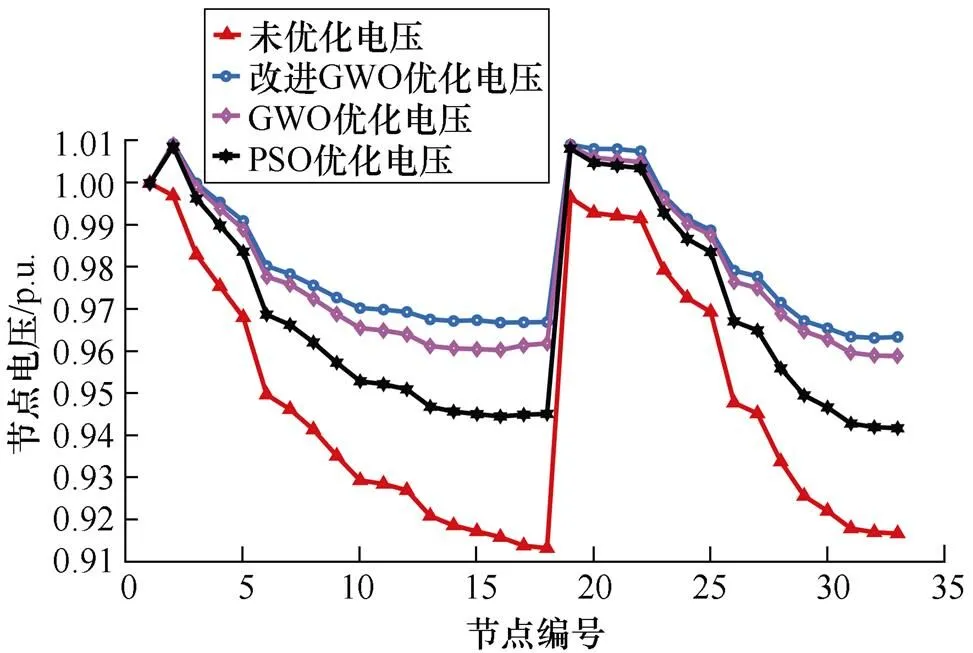
圖12 優化前后節點電壓曲線

由圖12可以看出，系統未優化前電壓降幅很大，電壓質量差，而在加入智能算法后電壓質量得到了明顯提升；改進灰狼優化算法可使系統節點電壓抬升至0.97p.u.以上，在提升電壓水平的同時未出現電壓越界，很好地保證了電能質量與配電系統的安全穩定。

無功功率在輸電及配電網絡上的流動會引起有功網損，光伏的接入也會對網損產生影響；優化前后的有功網損累計曲線如圖13所示。

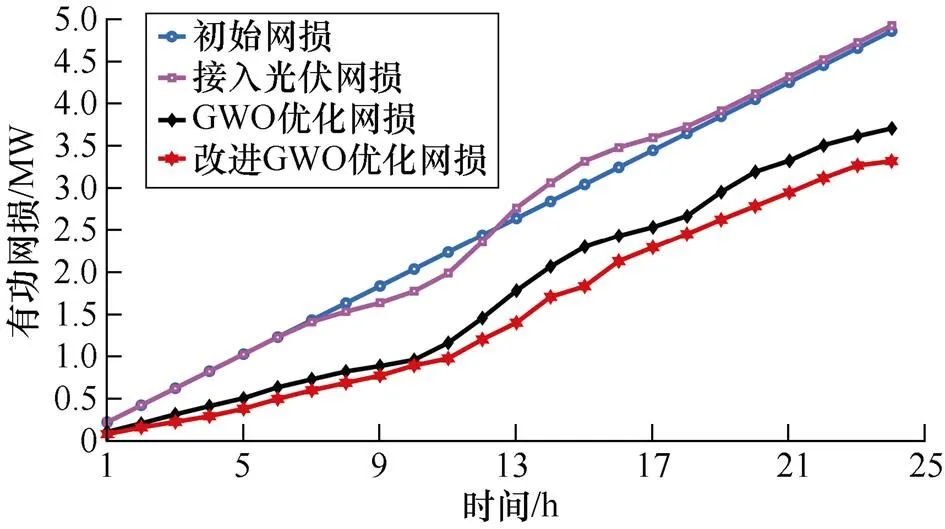
圖13 優化前后有功網損累計值曲線

從圖13可以看出，系統優化前的有功網損是一條直線，在光伏出力的時間里損耗會發生明顯波動。通過無功優化可使系統網損明顯降低，而且改進灰狼優化算法使網絡損耗更低，優化效果更好。

4 結論

本文針對光伏并網對配電網造成的電壓波動、線損增加，以及光伏和負荷出力的不確定性等問題，采用雙時間尺度動態無功優化，通過二階錐規劃將優化模型轉化為線性，并對不同控制設備采取不同控制策略進行調節，最后采用所提改進灰狼優化算法通過IEEE 33節點系統對含光伏接入的配電網進行仿真，結果表明：

1）在進行雙時間尺度構造時，通過對支路潮流進行二階錐松弛和離散型設備動作設限，并對SVG進行分時段調節，可以得到更好的優化效果和經濟性。

2）通過對算法初始化進行混沌學習、改進收斂因子，對最優粒子進行柯西擾動，并融合蜘蛛猴算法的位置更新，可以有效解決標準灰狼算法收斂緩慢、易陷入局部最優的問題。

[1] 丁俊, 王欣怡, 邵燁楠, 等. 新型電力系統的影響因素分析[J]. 電氣技術, 2022, 23(7): 42-45.

[2] 李桐, 韓學山. 時變追蹤并網光伏電站最大輸出功率的無功優化方法[J]. 電工技術學報, 2023, 38(11): 2921-2931.

[3] 黃偉達, 李天友, 黃超藝. 計及分布式光伏的農村配電臺區斷零故障分析[J]. 電氣技術, 2022, 23(2): 31-35.

[4] 張健, 王凱悅. 考慮電壓穩定性的含分布式電源配電網多目標無功優化[J]. 電氣技術, 2020, 21(3): 64-69.

[5] 王果, 武旭, 李龍, 等. 光伏多功能并網逆變器不同出力狀態下無功和諧波優化方法[J]. 電力自動化設備, 2024, 44(1): 80-87.

[6] 黃大為, 王孝泉, 于娜, 等. 計及光伏出力不確定性的配電網混合時間尺度無功/電壓控制策略[J]. 電工技術學報, 2022, 37(17): 4377-4389.

[7] 劉兆元, 王萍, 鄭能, 等. 考慮可控光伏系統的配電網有功-無功協調優化[J]. 電網技術, 2019, 43(1): 294-301.

[8] 黃偉, 劉斯亮, 王武, 等. 長時間尺度下計及光伏不確定性的配電網無功優化調度[J]. 電力系統自動化, 2018, 42(5): 154-162.

[9] CHAI Qingmian, ZHANG Cuo, XU Yan, et al. PV inverter reliability-constrained volt/var control of distribution networks[J]. IEEE Transactions on Sustainable Energy, 2021, 12(3): 1788-1800.

[10] 李勇, 姚天宇, 喬學博, 等. 基于聯合時序場景和源網荷協同的分布式光伏與儲能優化配置[J]. 電工技術學報, 2022, 37(13): 3289-3303.

[11] AI Yongle, DU Mingzhu, PAN Zhihang, et al. The optimization of reactive power for distribution network with PV generation based on NSGA-III[J]. CPSS Transactions on Power Electronics and Applications, 2021, 6(3): 193-200.

[12] XIE Yigong, ZHAI Suwei, LI Wenyun, et al. Active- reactive power coordinated optimization of distri- bution network with photovoltaic based on PSO-CSA algorithm[C]//2022 7th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 2022: 313-318.

[13] 羅荇子, 汪沨, 譚陽紅, 等. 改進小生境蝙蝠算法在無功優化中的應用[J]. 電力系統及其自動化學報, 2017, 29(10): 35-39, 51.

[14] 高鋒陽, 喬垚, 杜強, 等. 考慮光伏出力相關性的配電網動態無功優化[J]. 太陽能學報, 2018, 39(1): 101-109.

[15] 張曉鳳, 王秀英. 灰狼優化算法研究綜述[J]. 計算機科學, 2019, 46(3): 30-38.

[16] 薛陽, 燕宇鋮, 賈巍, 等. 基于改進灰狼算法優化長短期記憶網絡的光伏功率預測[J]. 太陽能學報, 2023, 44(7): 207-213.

[17] 夏正龍, 陸良帥, 吳啟凡, 等. 改進灰狼算法在含風電的配電網無功優化中的應用[J]. 智慧電力, 2023, 51(6): 63-70.

[18] 劉語忱, 閆群民, 郭陽, 等. 基于完備局部均值分解和相關分析的光伏發電側電-氫混合儲能優化配置[J]. 電氣技術, 2022, 23(11): 21-29.

[19] 郭清元, 吳杰康, 莫超, 等. 基于混合整數二階錐規劃的新能源配電網電壓無功協同優化模型[J]. 中國電機工程學報, 2018, 38(5): 1385-1396.

Dynamic reactive power optimization of photovoltaic distribution network based on improved gray wolf optimization algorithm

YU Huijun MA Fanshuo CHEN Gang YANG Chize LI Jiaxuan

(College of Electrical and Information Engineering, Hu’nan University of Technology, Zhuzhou, Hu’nan 412007)

In view of the problems caused by photovoltaic grid connection to the distribution network, such as voltage fluctuations, increased line losses, and uncertainty in photovoltaic and load output, this paper constructs a linear convex optimization model based on second-order cone programming. By controlling the on-load voltage regulating transformer and the capacitor bank action, photovoltaic inverter and static var generator reactive power compensation capacity constraints are dynamically analyzed on the day-ahead and intra-day dual time scale reactive power optimization model, which simplifies the solution process and increases the possibility of finding the global optimum. An improved gray wolf algorithm based on chaotic learning initialization, nonlinear convergence factor, optimal particle Cauchy perturbation and spider monkey algorithm position update method is proposed to prevent falling into local optima and enhance global search capabilities. Finally, the algorithm is used to model and simulate the IEEE 33 node system containing photo-voltaic. The results show that the algorithm has the advantages of high optimization efficiency and fast con-vergence speed. The feasibility and effect of the proposed algorithm are confirmed.

distribution network; photovoltaic power generation; dynamic reactive power optimization; second-order cone programming; gray wolf optimization (GWO)

2023-12-11

2023-12-19

于惠鈞（1975—），男，博士，教授，碩士生導師，研究方向為電氣分析與仿真、系統保護與自動化技術。

湖南省教育廳科學研究項目（20A162）

湖南省自然科學基金項目（2021JJ50052）