基于灰色BP 神經網絡的電力碳排放峰值預測

吳海杰，王聯智，謝敏，王康桑，符藝超

（南方電網海南數字電網研究院有限公司，海南海口 570203）

現階段，我國經濟發展過程中面臨著許多環境問題，其中最為緊要的問題是發電公司的二氧化碳排放量較高。因此，如何正確地預測碳排放峰值，結合預測結果制定碳減排策略，并在短時間內控制碳排放峰值，這均成為了現代社會發展過程中急需解決的問題。目前，學者們從不同的角度和理論出發，研究碳排放峰值預測方法。文獻[1]提出了基于STIRPAT 模型的峰值預測方法，在能源結構優化模式下構建了STIRPAT 模型。該模型結合VSTE 算法計算電力碳排放平均值，進而預測碳排放峰值。然而，該方法過分依賴人工操作，使得構建的模型在求解過程中受到不同因素影響，出現了較大預測誤差。文獻[2]提出了基于雙回歸預測模型的峰值預測方法。構建了電力碳排放雙回歸預測模型，根據電力耗能情況，將不同電力設備運行參數進行了相關處理，并將其輸入到預測模型中，實現電力碳排放峰值精準預測。該方法雖然能夠快速取得預測結果，但在實際操作過程中無法很好控制碳排放總量，因此預測結果還存在一定的誤差。

針對上述方法所以存在的問題，提出了基于灰色BP 神經網絡的電力碳排放峰值預測方法。灰色BP 神經網絡具有較好的非映射性能，還能夠根據實際情況靈活地設定參數，能夠降低預測誤差，提升預測精度。

1 基于灰色BP 神經網絡的預測模型構建

基于誤差反傳播的灰色BP 神經網絡具有連續逼近函數極限值的優勢，使得預測結果存在最優解[3]。此外，還可以根據不同環境設定模型結構的層數、單元數及訓練因子等，使預測過程更具有靈活性和隨機性，提升預測精準度與效率。灰色BP 神經網絡能夠訓練大量數據，并明確數據之間的關系[4-5]。采用快速下降方法通過反向傳遞不斷地調節網絡權值和門限，從而減小網絡的誤差。該方法的核心思想是引入一種新的學習方法，通過對網絡逆向傳遞進行迭代修正和訓練，使得網絡輸出矢量與所需矢量保持一致。

灰色BP 神經網絡模型將隨機變量視為一定區間內變動的灰色變量，經過處理后累加序列都呈現指數增長趨勢[6]，該情況下的原始數據序列和累加序列分別為：

將原始數據序列和累加序列作為輸入值，構建基于灰色BP 神經網絡的碳排放峰值預測模型，如圖1 所示。

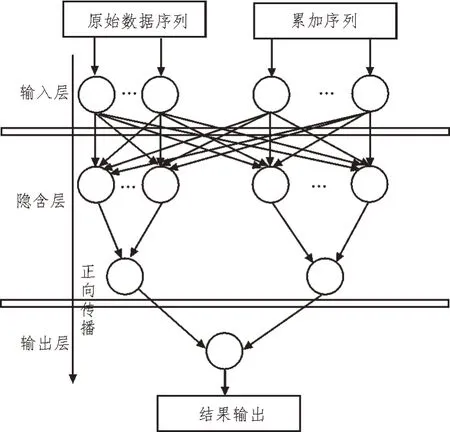
圖1 預測模型

在網絡輸出層的錯誤平方和小于規定值時，完成了模型訓練，以此能夠有效降低網絡加權次序偏差[7]。模型訓練具體步驟是：通過對各個節點初始化，隨機地分配各個節點權重和門限。在參數設定完成的情況下，分別對輸入層和輸出層連接權重和閾值進行計算。選擇下一種輸入方式，反復迭代，直到網絡輸出結果符合規定為止。

2 電力碳排放峰值預測模型求解

為了求解電力碳排放峰值預測模型，在灰色BP神經網絡中引入了遞推算法，該算法通過選取隨機碳排放路徑，計算各個因子對應的影響權值，進而獲取相應路徑碳排放數值[8-9]。隨機選取的碳排放新路徑為：

式中，Li表示第i種碳排放量路徑；λ表示碳排放系數[10]；L′(ξ)表示碳排放路徑抽取函數[11]。在計算電力碳排放量過程中，使用遞推算法計算電力碳排放量，公式為：

式中，ai表示第i種電力消費模式；fi表示第i種電力折標系數；λi表示第i種電力碳排放系數；j表示電力設備數量。

遞推算法采用的是隨機選擇電力碳排放路徑方式，主要是通過對不同路徑上碳排放影響因素分析，獲取最大和最小碳排放周期[12]。具體的操作流程如下：

步驟一：隨機獲取各路徑碳排放量，通過引入微分方程參數，對其進行加權處理，得到了新的灰色BP 神經網絡模型。

步驟二：采用正規化的方法剔除了數據之間的非線性關系，并將其引入到模型中。利用Lasso 回歸分析方法，分析了各因素對碳排放量峰值預測的影響[13-14]。Lasso 回歸分析通過懲罰函數來壓縮模型中的系數，將一些因子變成0，以篩選出顯著變量。

設a為自變量，b為因變量，經過m次取樣后得到的預測樣本標準值為(a,b)，自變量a的第k個預測值為：

式中，T表示預測周期。因變量對自變量的回歸模型可表示為：

式中，εi表示隨機自然數。如果要篩選出影響顯著變量，需要給該公式添加一個條件，約束表達式為：

式中，t表示調和參數；φ表示最佳調整閾值。Lasso 回歸就是通過不斷調整調和參數值，降低回歸系數，壓縮變量系數直到為0，以此獲取顯著變量，即碳排放峰值[15]。

步驟三：由于電力碳排放量計算具有鄰接性，因此在計算一個節點的碳排放量時，僅需獲得鄰近節點碳排放量，無需了解該節點碳排放流信息，碳排放流鄰接特性示意圖，如圖2 所示。

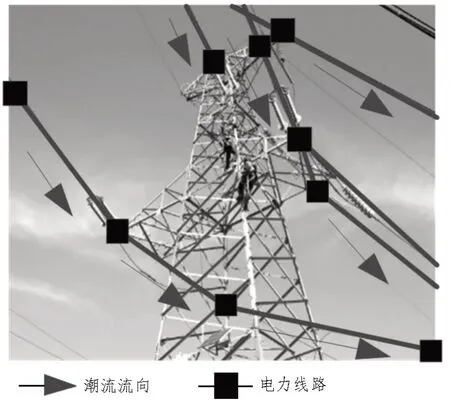
圖2 碳排放流鄰接特性示意圖

通過對各節點功率分配，可以得出各節點間的聯系。根據電網碳排放鄰接性，依次求取初始點到不同節點的碳勢。在每次遞推時，在確定某一節點碳勢后，就可求取全部節點碳勢。因此，每一次遞推都能在任意一段時間內獲取精準的節點碳勢計算結果。最終，利用有限遞推方法，求出了網絡中全部節點碳勢[16]。具體計算公式如下：

式中，Pi表示節點注入的有功功率；Gj表示電力機組支路有功功率；Ωi、Ωj分別表示第i、j兩個電力碳排放及節點注入的集合。判斷是否所有節點都已經輪詢完畢，若是獲取了全部節點碳勢，完成遞推。

步驟四：在偏差允許的條件下，實現了預測模型的求解，得到了電力碳排放量峰值預測結果。

3 實驗

為了驗證研究的基于灰色BP 神經網絡的電力碳排放峰值預測方法是否合理，設計了相關實驗，以此來驗證方法的可行性。

3.1 實驗過程

分析了電力碳排放流，其示意圖如圖3 所示。

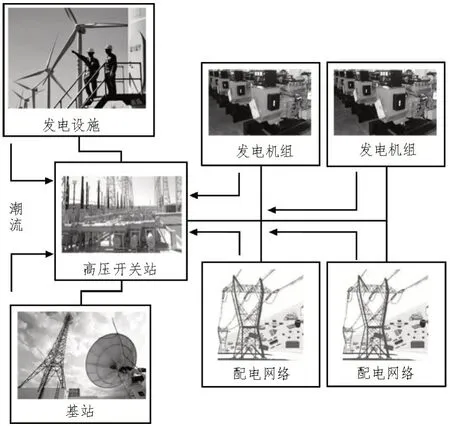
圖3 電力碳排放流示意圖

通過分析配電網絡與主網功率交換方向及規模，確定各主要網絡間的碳排放量的計算次序。若將有功電力注入到主網，則可將其作為主網供電，而不能作為主網負荷。若將有功電力注入到主網配電網絡中，利用分布式電源與常規火電廠之間邊界信息，對配電網絡中碳排放進行分析。在此基礎上，將根節點的碳勢和注入功率作為主網的重要變量，對主要網絡碳排放量進行了計算。根據主網碳排放流量分析了其碳排放流的分布。

3.2 實驗數據分析

碳排放峰值不是表示一年碳排放量達到峰值，而是從這一年開始某個地區碳排放量出現穩定趨勢。在基準情景、低碳情景和強化低碳情景下，采集碳排放峰值如表1 所示。

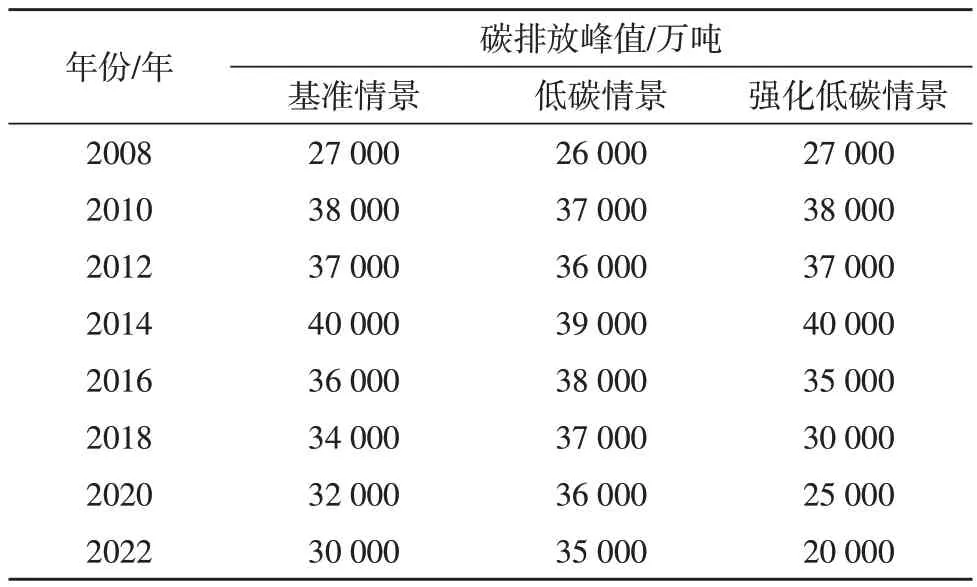
表1 碳排放峰值采集結果

由表1 可知，基準情景、低碳情景和強化低碳情景下碳排放峰值分別為40 000 萬噸、39 000 萬噸、40 000 萬噸，在2014-2022 年三種情景的碳排放均呈緩慢下降趨勢。

3.3 實驗結果與分析

檢驗文獻[1]方法、文獻[2]方法和研究方法的電力碳排放峰值預測結果，如圖4 所示。

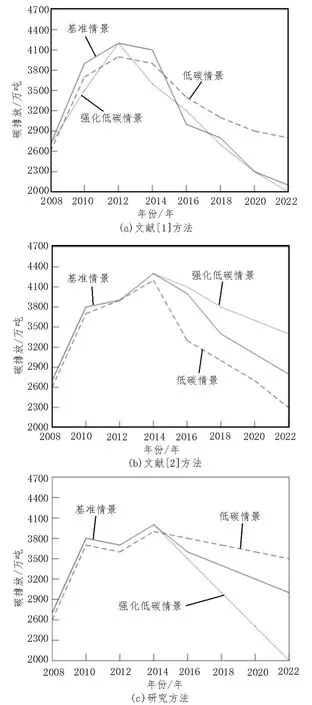
圖4 三種方法峰值預測結果

由圖4(a)可知，在基準情景下文獻[1]方法碳排放峰值與表1 數據存在最大為600 萬噸的誤差；在低碳情景下文獻[1]方法碳排放峰值與表1 數據存在最大為500 萬噸的誤差；在強化低碳情景下文獻[1]方法碳排放峰值與表1 數據存在最大為400 萬噸的誤差。由圖4(b)可知，在基準情景下文獻[2]方法的碳排放峰值與表1 數據存在最大為400 萬噸的誤差；在低碳情景下文獻[2]方法的碳排放峰值與表1 數據存在最大為500 萬噸的誤差；在強化低碳情景下文獻[2]方法的碳排放峰值與表1 數據存在最大為600萬噸的誤差。由圖4(c)可知，使用所研究方法在三種情景下的碳排放峰值與表1 數據一致。

通過上述分析結果可知，使用所研究方法電力碳排放峰值與實際數據一致，說明該方法的預測結果更為精準。

4 結束語

由于碳排放變化趨勢呈現非線性，灰色BP 神經網絡進行碳排放峰值預測，原因在于灰色BP 神經網絡具有較好非映射性能，還能夠根據實際情況靈活地設定參數，使用Lasso 回歸篩選法和遞推算法對該模型進行了求解，得到了相關的電力碳排放峰值預測結果。實驗結果表明，在基準情景、低碳情景和強化低碳情景下，所研究方法的碳排量峰值與實際數值一致，都為40 000 萬噸、39 000 萬噸、40 000 萬噸，由實驗驗證了所研究方法的合理性，能夠為碳排放控制提供技術支持。