無回答與計量誤差疊加時總體方差的校準估計

龐智強，牛璽娟，，王朝旭

（1.蘭州財經大學統計與數據科學學院，蘭州 730020；2.青海師范大學數學與統計學院，西寧 810008）

0 引言

在抽樣理論中，研究者要處理兩種類型的調查誤差：抽樣誤差和非抽樣誤差。其中，抽樣誤差是由抽樣的隨機性引起的誤差，非抽樣誤差是除抽樣以外的其他原因引起的誤差。在經典的抽樣理論中，研究的估計誤差主要是抽樣誤差，對非抽樣誤差研究較少。在估計總體未知參數時，非抽樣誤差在一定程度上比抽樣誤差更容易影響估計量的性質。

在抽樣調查中，通常假設所有選定的單位都將全部參與調查，并且所有記錄的結果都是對變量的真實測量。然而，由于客觀條件的限制，難以完全避免非抽樣誤差的出現，使得調查得到的數據并不完整，從而會導致出現嚴重的錯誤推斷。總體方差估計作為統計推斷中非常重要的研究內容，同樣存在上述困擾。因此，有必要開發能夠最大限度應對非抽樣誤差影響的總體方差估計方法。

無回答誤差和計量誤差作為兩種重要的非抽樣誤差，對總體方差的估計結果會產生至關重要的影響。無回答誤差是估計研究變量總體方差過程中面臨的重大挑戰之一。Hansen 和Hurwitz（1946）[1]考慮了存在無回答誤差時有限總體均值的估計問題；Chaudhuri 和Pal（2015）[2]提出了不同總體參數的估計量；Ahmeda 和Pal（2005）[3]探究了簡單隨機抽樣下存在隨機無回答時總體方差的估計問題；Singh等（2012）[4]針對兩種不同的隨機無回答，提出了總體方差的估計量；牛成英和龐志強（2014）[5]運用概率分析方法討論了無回答對總體參數估計量抽樣方差的影響。

除了無回答之外，估計總體方差時遇到的另一大挑戰是計量誤差。Singh 和Karpe（2009）[6]討論了計量誤差影響下總體方差的估計問題。在實際調查中，研究人員經常面臨一些調查單元既存在無回答又有計量誤差的情況。Tiwari等（2023）[7]討論了無回答和計量誤差疊加時有限總體均值的估計問題。

輔助變量在抽樣調查中起著關鍵作用，恰當使用輔助信息能有效提高總體參數估計的準確性。使用輔助變量估計方差的技術最早由Das（1978）[8]提出，他重點討論了已知輔助變量變異系數情況下的方差估計。隨后Isaki（1983）[9]又將這一技術進行推廣，探討了當研究變量和輔助變量線性相關時總體方差的比率估計問題。當輔助信息可用時，總體參數的校準估計方法也被廣泛應用于抽樣調查。自Deville 和Sarndal（1992）[10]首次提出校準估計方法以來，該方法已成為統計學研究的一個重要課題。Tracy 等（2003）[11]、Singh 等（2020）[12]利用校準估計，提出了不同抽樣設計下總體參數的校準估計量。Plikusas 和Pumputis（2007）[13]將校準估計的思想應用到總體協方差估計中，得到了不同約束條件下總體協方差的校準估計量。

本文考慮了無回答和計量誤差疊加存在時有限總體方差的估計，并基于校準估計方法提出了分層隨機抽樣中方差的校準估計策略。在數值分析方面，從模擬和真實數據兩個方面對所提校準估計量的性能進行了檢驗。

1 抽樣基礎理論

1.1 抽樣框架

考慮一個容量為N的有限總體U，U={U1，U2，…，UN}，現按照一定的標準對總體U進行分層，將其劃分為L個互不相交的層，使得，h=1，2，…，L。設Y為研究變量，X、Rx分別為第一、第二輔助變量，其中，Rx為輔助變量X的秩。

本文采用無放回簡單隨機抽樣方法（SRSWOR），抽樣分兩個階段進行。第一階段：先從第h層的總體Nh中抽取容量為nh的簡單隨機樣本，且各層間的抽樣均相互獨立；再將每層得到的樣本組合為一個新樣本，稱該樣本為初始樣本，記為Snh，h=1，2，…，L。設在第一階段的nh個樣本中，共有r1h個單元發生無回答。第二階段：從初始樣本Snh提供回答的部分中進行抽樣，同樣利用SRSWOR方法抽取一個容量為mh的樣本，記為Smh。設在第二階段的mh個樣本中，共有r2h個單元發生無回答。

1.2 符號說明

本文中所用到的一些符號及其含義如下：

：研究變量Y對應的總體方差。

：第h層的校準權重，h=1，2，…，L。

Qh：第h層的獨立權重，h=1，2，…，L。

1.3 隨機無回答的概率分布

考慮第h層的情況：在第一階段容量為nh的初始樣本Snh中，設r1h表示由于隨機無回答而無法獲得信息的抽樣單元數，則r1h可能的取值為0，1，2，…，nh-2。同理，設r2h為第二階段容量為mh的樣本Smh中發生無回答的抽樣單元數，則r2h可能的取值為0，1，2，…，mh-2，且0 ≤r1h≤nh-2，0 ≤r2h≤mh-1。假設p1和p2分別表示nh-2 和mh-2 個可能值中發生無回答的概率，則r1h和r2h均為離散型隨機變量，他們服從如下概率分布[3]：

其中，q1=1-p1，q2=1-p2。

2 校準估計量的構建

在本文中，假設無回答和計量誤差僅存在于研究變量Y和輔助變量X之間，而不存在于研究變量Y和輔助變量的秩Rx之間。Singh等（2020）[12]給出了分層隨機抽樣設計下有限總體方差的校準估計方法，其校準估計量的一般形式如下：

基于上述討論，本文提出了一種改進的校準估計量：

其中，是在新校準約束條件下最小化卡方距離得到的校準權重。

考慮各層估計量的一個復合類Th，

使得對函數g，成立。

2.1 校準估計方法

在分層隨機抽樣中，校準估計方法主要用于獲得最優層權。為了得到合理的校準權重，要保證校準權重與原始權重Wh盡可能地接近。因此，需要建立校準權重與原始權重Wh之間的距離函數關系，一般選擇比較簡單的卡方距離作為兩個權重之間的距離函數。在校準估計中，最小化距離函數即為最優化目標函數，拉格朗日乘數法是經常被用來求解最優化問題的一種方法。即要使卡方距離在校準約束條件下達到最小值。

本文用拉格朗日乘數法求解，結合卡方距離函數和校準約束條件，構造最優化問題的拉格朗日函數如下：

其中，λ1，λ2，λ3為拉格朗日乘子。

對式（3）兩邊關于求偏導，得:

將式（5）中的解代入校準約束條件中，根據等式關系可計算得到對應的拉格朗日乘子值為:

其中，det=aeh-af2-b2h+2bcf-c2e，det1=deh-df2-bgh+bif+cgf-cie，det2=agh-aif-bdh+cdf+bci-c2g，det3=aei-agf-b2i+bcg+bdf-cde。

常數a，b，c，d，e，f，g，h，i定義如下：

將計算得到的拉格朗日乘子值λ1，λ2，λ3代入式（5）中，便可得到最終的校準權重的值。

2.2 估計量的偏差和均方誤差

為了得到校準估計量Tst(P)的偏差及其均方誤差MSE 的表達式，作如下變換:

其中，d1h，d2h，d3h，d4h為函數在點處的一階偏導數；同理，d11h，d22h，d33h，d44h，d12h，d13h，d14h，d23h，d24h，d34h為函數在點處的二階偏導數。

為計算方便，此處附加一個約束條件：

現將式（7）至式（9）代入式（6），并用相對誤差eih,i=0，1，2，3 的形式表示式（6），可得：

將式（10）代入式（3），則校準估計量Tst(P)可寫為：

對式（11）作簡單變換，然后兩邊同時取期望，得到校準估計量Tst(P)的偏差為：

進一步，得到一階近似下校準估計量Tst(P)的MSE，其表達式如下：

對式（13）分別關于d2h，d4h求偏導，并令其偏導數等于0，得到d2h，d4h的最優解：

將式（14）代入式（13）中，得到Tst(P)最小的MSE：

令(xhi，yhi)和(Xhi，Yhi)分別為二元變量(X，Y)在第h層第i個單元對應的觀測值和真實值，則研究變量Y與輔助變量X的計量誤差分別為Uhi=yhi-Yhi與Vhi=xhi-Xhi，且計量誤差Uhi與Vhi之間不相關。令、分別為研究變量Y、輔助變量X對應的計量誤差的總體方差，可以得到當計量誤差存在時估計量Tst(P)最小的MSE：

3 數值分析

本文從模擬數據和真實數據兩個方面對所提校準估計量Tst(P)與現有校準估計量Tst(S)的性能進行比較。

3.1 模擬研究

在統計軟件R 中進行模擬研究，對估計量的估計效果進行對比分析。將校準權重Ωh代入式（1），通過計算分別得到不存在和存在計量誤差兩種情形下估計量Tst(S)最小的MSE：

本文使用估計量的百分比相對效率（PRE）作為估計量的評價指標：

模擬數據中的總體參數說明見表1。為了使模擬過程順利實施，本文采用了Singh 軟件包中MASS 中的函數mvrnorm 生成服從正態分布的數據[12]。對于不同的控制參數Qh，在R 中進行1000 次循環，控制參數Qh的取值有六種情形。情形1：Qh=1.0。情形2：情形3：Qh=。情形4：Qh=。情形5：Qh=。情形6：Qh=。

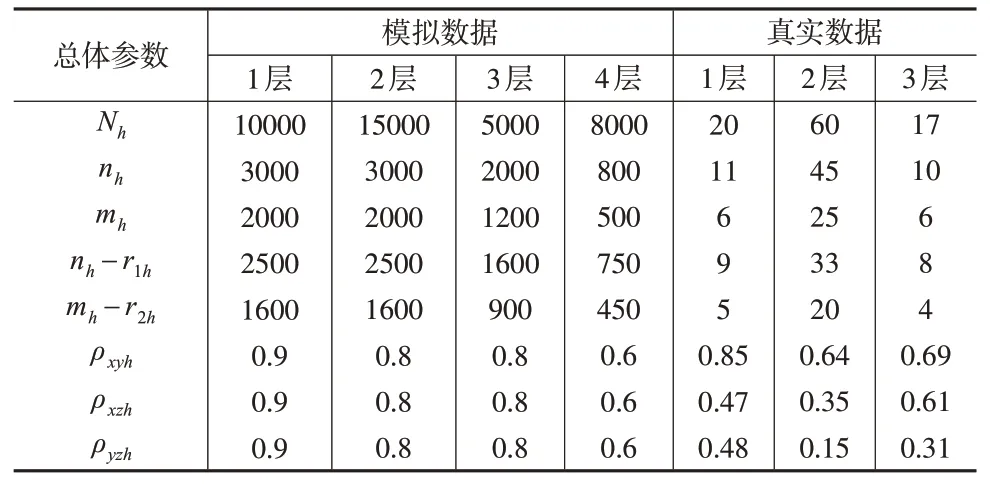
表1 總體參數說明

對于隨機無回答的概率p1和p2，令他們分別取0.05、0.10、0.15 和0.20 四個值。下頁表2 和表3 分別給出了校準前后的權重和PRE的模擬結果。

表2 模擬數據下校準前后權重對比

表3 模擬數據下的PRE結果

3.2 真實數據的應用

為研究校準估計量的實際應用性能，考慮一個真實數據集。為了盡可能準確地估計總體方差，本文有意考慮研究變量中某些數據的缺失，真實數據的總體參數情況仍然在表1中給出。

用于數值研究的總體來源于文獻[14]。數據可在R軟件的faraway軟件包中的prostate文件中獲得。

根據控制參數Qh，分別在不存在計量誤差和存在計量誤差兩種情況下取不同值，真實數據在校準前后的權重和PRE分別在表4和下頁表5中給出。

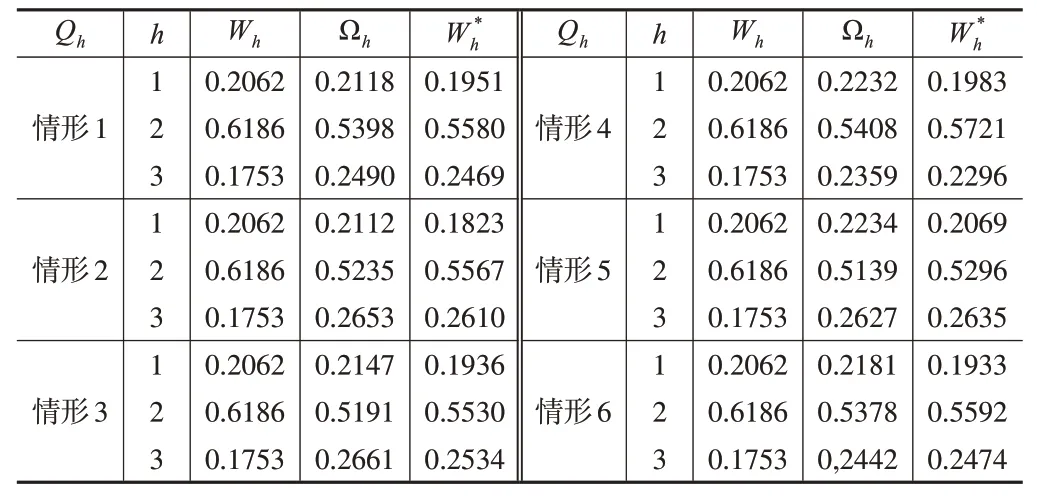
表4 真實數據下校準前后權重對比

綜合表2至表5的結果，可以看出：

（1）從表2和表4可以看出，使用校準方法得到的權重與原始權重非常接近。這表明校準技術可以有效地優化權重，提高校準估計量的估計精度。此外，從表3 和表5可以看出，對于每個控制參數Qh，本文提出的校準估計量Tst(P)總是比Singh的校準估計量Tst(S)更有效。且對于無回答的概率p1，p2而言，當p1，p2∈(0.05，0.10) 時，校準估計量最有效。

（2）無論是模擬數據還是真實數據，存在計量誤差的PRE都小于不存在計量誤差的PRE。從表5還可以看出，在分層隨機抽樣下，無論Qh取何值，本文所提校準估計量Tst(P)在存在計量誤差和不存在計量誤差兩種情況下，都優于現有校準估計量Tst(S)。

4 結束語

本文關注的是無回答和計量誤差疊加存在時分層隨機抽樣中有限總體方差的估計問題。通過模擬分析和實際數據的應用研究可以發現，本文所提出的校準估計量Tst(P)在最小化非抽樣誤差的負面影響方面總是比現有校準估計量Tst(S)更有效。

在非抽樣誤差和總體方差估計方面，還存在一些重要的問題值得考慮：（1）本文僅考慮了分層隨機抽樣中無回答和計量誤差同時存在時有限總體方差的估計，除分層隨機抽樣外，還可以考慮更多的抽樣設計。（2）受模擬結果的啟發，同時也考慮到處理非抽樣誤差問題的重要性，可以鼓勵統計調查人員適當使用本文提出的校準估計量，將其應用于社會經濟調查中。例如：估計社會不同階層在節假日的開支變化，估計全國不同地區婦女的收入變化，等等。