含多項式取絕對值函數(shù)的混沌系統(tǒng)分析與應(yīng)用

高正中　杜翔

摘要： 為獲得更復(fù)雜的動力學(xué)特性，設(shè)計了一種含有三次多項式取絕對值函數(shù)的混沌系統(tǒng)，該混沌系統(tǒng)的理論模型由含有3個狀態(tài)變量的非線性方程組描述。分析了該系統(tǒng)的基本屬性，以及相軌圖、時域波形、Lyapunov指數(shù)、Poincaré映射、分岔圖等動力學(xué)特性。系統(tǒng)在一定的參數(shù)條件下存在周期和混沌的特性，初值對稱時存在共存吸引子或聚合吸引子。此外，某些系統(tǒng)參數(shù)變化時，系統(tǒng)存在恒定的動力學(xué)特性，狀態(tài)變量初值變化時系統(tǒng)的動力學(xué)特性也是恒定的。電路仿真驗證了理論的正確性。基于新設(shè)計的混沌系統(tǒng)設(shè)計了一種加密方案，對加密性能進行了分析，表明了加密方案的有效性。

關(guān)鍵詞： 混沌；動力學(xué)；共存吸引子；共存分岔；圖像加密

中圖分類號： TP271.62?????? 文獻標識碼： A

Analysis and Application of Chaotic System with Polynomial Absolute Valued Function

GAO Zhengzhong，DU Xiang

（College of Electrical Engineering and Automation， Shandong University of Science and Technology， Qingdao 266510， China）

Abstract：In order to get more complex dynamical properties， a chaotic system with cubic polynomial taking absolute value function is designed. The theoretical model of the chaotic system is described by a set of nonlinear equations with three state variables. The basic properties and the dynamic characteristics of the system like phase diagram， time domain waveform， Lyapunov exponent， Poincaré map and bifurcation diagram are analyzed. Under certain parameter conditions， the system has periodic and chaotic properties， and there are coexistence attractors or aggregation attractors when the initial values are symmetrical. In addition， when some system parameters change， the system has constant dynamic characteristics， when the initial value of the state variable changes， the dynamic characteristics of the system also remain unchanged. The correctness of the theory is verified by circuit simulation. Based on the newly designed chaotic system， an encryption scheme is designed， and the encryption performance is analyzed， which shows the effectiveness of the encryption scheme.

Keywords： chaos; dynamics; coexisting attractors; coexisting bifurcation; image encryption

0 引言

1963年，美國氣象學(xué)家Lorenz在研究天氣預(yù)報時，把大氣動力學(xué)方程組進行簡化并在計算機上進行模擬實驗，發(fā)現(xiàn)舍去小數(shù)點后幾位數(shù)字的模型與未舍去的模型迥然不同[1]，于是他得出了“短期的天氣預(yù)報可行，但長期不可行”的結(jié)論。Lorenz研究天氣預(yù)報時提出了“蝴蝶效應(yīng)”與混沌理論。這一理論表明確定性系統(tǒng)可以產(chǎn)生復(fù)雜的、類似隨機的運動。自此，諸多學(xué)者紛紛開展了大量的研究。混沌理論已廣泛應(yīng)用于圖像加密[24]、保密通信[57]和神經(jīng)網(wǎng)絡(luò)[810]等領(lǐng)域。師東生等[11]構(gòu)建了一個在兩個方向上具有四翼特征的五維超混沌系統(tǒng)。鮮永菊等[12]構(gòu)造了一個四維超混沌系統(tǒng)，該系統(tǒng)有豐富的多穩(wěn)態(tài)特性與多翼吸引子，最多有12種吸引子共存的情況。Yang等[13]從一個三維混沌系統(tǒng)出發(fā)，加入3個線性動態(tài)控制器得到了六維混沌系統(tǒng)，該系統(tǒng)有隱藏超混沌等復(fù)雜現(xiàn)象。Ma等[14]在三維自治混沌系統(tǒng)中加入平滑磁通控制的憶阻器和交叉項，設(shè)計了一種可以產(chǎn)生四翼混沌吸引子的新型四維超混沌系統(tǒng)。Qi等[15]從Lorenz系統(tǒng)出發(fā)，提出了一種每個狀態(tài)方程都含有一個二次交叉項的新型混沌系統(tǒng)，該混沌系統(tǒng)有不動點、周期環(huán)、混沌等多種吸引子。Atiyeh等[16]提出了一個具有平衡面的四維混沌系統(tǒng)。Bao等[17]在亞遺傳混沌Jerk電路里引入了一個憶阻器，得到了一個新型混沌電路，在系統(tǒng)狀態(tài)變量初值不同時，系統(tǒng)有完全不同的動力學(xué)行為。Chen等[18]利用切換函數(shù)生成了環(huán)形、球形混沌吸引子。臧鴻雁等[19]給出了一個分段線性混沌映射，并分析了其與一個三次多項式映射拓撲共軛的充分條件。高秉建[20]通過增加第二類鞍焦平衡點的數(shù)目提出了一種新的生成多翼混沌吸引子的方法。

目前，含有多項式取絕對值的非線性函數(shù)并能產(chǎn)生共存吸引子且無憶阻器的混沌系統(tǒng)鮮有報道。不含有多穩(wěn)態(tài)現(xiàn)象的混沌系統(tǒng)，動力學(xué)特性的復(fù)雜程度較低，實際應(yīng)用時效果稍差，雖然憶阻系統(tǒng)可以產(chǎn)生共存吸引子，但憶阻器沒有完全商用化，制備成本高，因此這樣的混沌系統(tǒng)在物理實現(xiàn)時，成本自然很高。本文設(shè)計了一個表達式中含有三次多項式取絕對值的混沌系統(tǒng)，對系統(tǒng)進行了基本特性考察、動力學(xué)特性分析，發(fā)現(xiàn)系統(tǒng)存在共存吸引子或聚合吸引子，這降低了含共存吸引子的混沌系統(tǒng)的物理實現(xiàn)成本。并且進行了電路仿真，最后基于該系統(tǒng)設(shè)計了一種加密方案并驗證了其有效性。

1 混沌系統(tǒng)描述

本文設(shè)計的混沌系統(tǒng)表達式：

其中，狀態(tài)變量由x，y，z表示，系統(tǒng)參數(shù)由a，b，c，d，e，f，g表示。所有系統(tǒng)參數(shù)均大于0。

2 基本特性與動力學(xué)行為分析

2.1 系統(tǒng)相圖、時域波形、Poincaré映射圖

在系統(tǒng)狀態(tài)方程中，若取a=4，b=5，c=4，d=0.1，e=1，f=1，g=7，并且系統(tǒng)初始條件設(shè)定為（x0，y0，z0）=（-1，-1，-1）時，系統(tǒng)產(chǎn)生的吸引子如圖1所示。分析圖1可知：系統(tǒng)的運動軌跡是雜亂無章的，同時可以發(fā)現(xiàn)吸引子具有渦卷結(jié)構(gòu)，其吸引子屬于混沌吸引子。

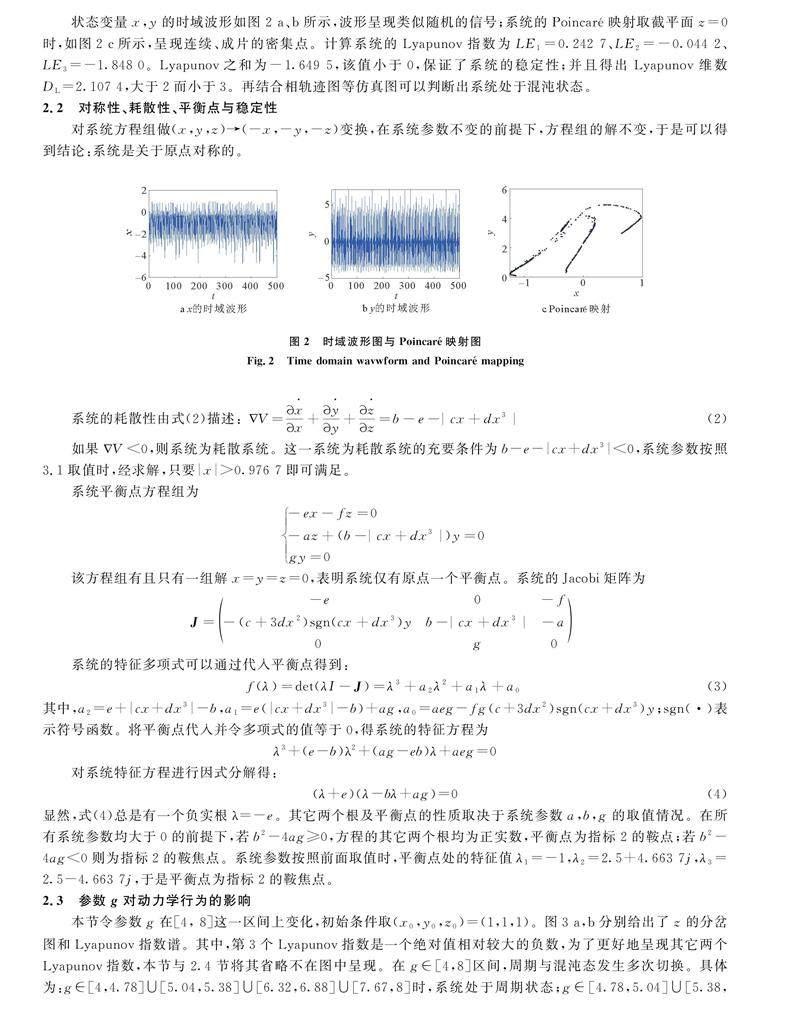
狀態(tài)變量x，y的時域波形如圖2 a、b所示，波形呈現(xiàn)類似隨機的信號；系統(tǒng)的Poincaré映射取截平面z=0時，如圖2 c所示，呈現(xiàn)連續(xù)、成片的密集點。計算系統(tǒng)的Lyapunov指數(shù)為LE1=0.242 7、LE2=-0.044 2、LE3=-1.848 0。Lyapunov之和為-1.649 5，該值小于0，保證了系統(tǒng)的穩(wěn)定性；并且得出Lyapunov維數(shù)DL=2.107 4，大于2而小于3。再結(jié)合相軌跡圖等仿真圖可以判斷出系統(tǒng)處于混沌狀態(tài)。

2.2 對稱性、耗散性、平衡點與穩(wěn)定性

對系統(tǒng)方程組做（x，y，z）→（-x，-y，-z）變換，在系統(tǒng)參數(shù)不變的前提下，方程組的解不變，于是可以得到結(jié)論：系統(tǒng)是關(guān)于原點對稱的。

顯然，式（4）總是有一個負實根λ=-e。其它兩個根及平衡點的性質(zhì)取決于系統(tǒng)參數(shù)a，b，g的取值情況。在所有系統(tǒng)參數(shù)均大于0的前提下，若b2-4ag≥0，方程的其它兩個根均為正實數(shù)，平衡點為指標2的鞍點；若b2-4ag<0則為指標2的鞍焦點。系統(tǒng)參數(shù)按照前面取值時，平衡點處的特征值λ1=-1，λ2=2.5+4.663 7j，λ3=2.5-4.663 7j，于是平衡點為指標2的鞍焦點。

2.3 參數(shù)g對動力學(xué)行為的影響

本節(jié)令參數(shù)g在[4， 8]這一區(qū)間上變化，初始條件取（x0，y0，z0）=（1，1，1）。圖3 a，b分別給出了z的分岔圖和Lyapunov指數(shù)譜。其中，第3個Lyapunov指數(shù)是一個絕對值相對較大的負數(shù)，為了更好地呈現(xiàn)其它兩個Lyapunov指數(shù)，本節(jié)與2.4節(jié)將其省略不在圖中呈現(xiàn)。在g∈[4，8]區(qū)間，周期與混沌態(tài)發(fā)生多次切換。具體為：g∈[4，4.78]∪[5.04，5.38]∪[6.32，6.88]∪[7.67，8]時，系統(tǒng)處于周期狀態(tài)；g∈[4.78，5.04]∪[5.38，6.32]∪[6.88，7.67]時，系統(tǒng)處于混沌狀態(tài)。

由圖3b分岔圖知，系統(tǒng)經(jīng)歷了多次正向、反向的分岔。其中，當g∈[5.38，6.32]時，分岔圖顯示了一些狹窄的周期窗口。選取不同的參數(shù)g，系統(tǒng)在x-z平面上的相圖如圖4所示。

2.4 參數(shù)f對動力學(xué)特性的影響

與2.3節(jié)類似，令參數(shù)f在[2，14]區(qū)間上變化，進行分析。首先，從圖5a和b可以看出，首個Lyapunov指數(shù)一直大于0，第二根Lyapunov指數(shù)一直等于0，相圖中則總是有成片的密集點，表明系統(tǒng)一直處于混沌態(tài)。然后，僅改變一個系統(tǒng)參數(shù)，令g=5.2，圖5c和d重新給出了上述兩幅仿真圖，可以看出首個Lyapunov指數(shù)一直約等于0，第二根Lyapunov指數(shù)一直小于0，分岔圖中點分布得比較稀疏，意味著系統(tǒng)一直處于周期態(tài)，因此系統(tǒng)參數(shù)f變化時，根據(jù)其它系統(tǒng)參數(shù)取值的情況，系統(tǒng)具有持續(xù)混沌或持續(xù)周期的特性。

2.5 參數(shù)變化時持續(xù)動力學(xué)特性理論分析

由2.3和2.4的分析知道，系統(tǒng)參數(shù)g變化能影響系統(tǒng)的動力學(xué)行為，而系統(tǒng)參數(shù)f變化不影響。將系統(tǒng)的平衡點代入特征方程，參數(shù)c，d，f會完全消去。具體來說，當x=y=z=0時，特征方程的系數(shù)a2=e-b，a1=ag-be，a0=aeg，即特征方程的系數(shù)與參數(shù)c，d，f無關(guān)。從理論上來講，當這3個參數(shù)改變時，系統(tǒng)平衡點類型相同，擁有相同的動力學(xué)特性。

另外，由圖5b，d知，當系統(tǒng)參數(shù)f改變時，分岔一直在下降，且分岔圖或其上方輪廓類似反比例函數(shù)曲線，因此該系統(tǒng)參數(shù)改變時系統(tǒng)具有調(diào)幅特性。從理論上來說，系統(tǒng)參數(shù)c，d改變時，系統(tǒng)同樣具有調(diào)幅特性[2122]。

2.6 狀態(tài)變量初值對動力學(xué)行為的影響

本節(jié)中，令系統(tǒng)參數(shù)按照3.1取值，每次固定兩個狀態(tài)變量的初值等于1，第3個狀態(tài)變量初值在[-30，30]之間變化，從圖6所示的Lyapunov指數(shù)譜可以發(fā)現(xiàn)，3個狀態(tài)變量初值在[-30，30]這一區(qū)間上變化時，Lyapunov指數(shù)譜符號總為（+，0，-），因此，在一定的參數(shù)條件下，系統(tǒng)初值變化時存在持續(xù)混沌的特性。

2.7 系統(tǒng)的共存吸引子與共存分岔

共存吸引子、共存分岔也是混沌系統(tǒng)的重要特征。共存吸引子是指系統(tǒng)參數(shù)取相同數(shù)值而初值不相等的時候，所產(chǎn)生的不一樣的吸引子。其它系統(tǒng)參數(shù)按照3.1取值，改變g的數(shù)值，共存吸引子在x-y平面上的投影如圖7a～e所示。其中，紅色的軌跡為系統(tǒng)初值取（-1，-1，-2）時，系統(tǒng)的吸引子投影，藍色的軌線則對應(yīng)系統(tǒng)初值取（1，1，2）。x的共存分岔圖如圖7 f所示，紅色的部分對應(yīng)初值取（-1，-1，-2），藍色對應(yīng)系統(tǒng)初值取（1，1，2）。由圖7各圖可見，系統(tǒng)初值取對稱值時，g∈[5.38，6.32]系統(tǒng)產(chǎn)生聚合混沌吸引子，g∈[4，5.38]∪[6.32，8]時產(chǎn)生對稱共存吸引子。

3 系統(tǒng)的模擬電路仿真

模擬電路仿真通常在Multisim軟件平臺進行。首先，運算放大器的線性范圍為±13.5V，模擬乘法器線性范圍為±10V，因此需要對超過上述范圍的狀態(tài)變量z進行壓縮變換。設(shè)z→2z，變換后，式（1）轉(zhuǎn)化為

在電路的狀態(tài)方程中，首先取電容C1=C2=C3= 10nF，R4=R5=R8=R10=R11=R12=R13=R15=R16=R17=R19 =10kΩ，對比系統(tǒng)方程和電路狀態(tài)方程，得

1R1C1=1 000，1R2C1=2 000，1R3C2=8 000，1R6C2=5 000，1R18C2=4 000，1100R14C2=100，1R20C3=3 500

進而可求得R1=100kΩ，R2=50kΩ，R3=12.5kΩ，R6=20kΩ，R14=10kΩ，R18=25kΩ，R20=28.571kΩ。取R20=28.7kΩ，其它電路元件按照計算結(jié)果取值，令3個電容的初始電壓均取-1V，即設(shè)定系統(tǒng)初值為（x0，y0，z0）=（-1，-1，-1），y-x平面、y-z平面的仿真實驗結(jié)果如圖9所示，證明了理論的正確性。

4 系統(tǒng)在圖像加密中的應(yīng)用

本加密解密算法基于新設(shè)計的混沌系統(tǒng)，結(jié)合了像素置亂和擴散的算法。像素置亂可以使得像素點偏離原始位置，使相鄰像素相關(guān)程度下降；而擴散可以改變像素的灰度值，影響圖像的統(tǒng)計特性。

本加密解密算法分為4部分——一個混沌密碼發(fā)生器、兩個明文無關(guān)的擴散算法和一個明文關(guān)聯(lián)的置亂算法。加密解密過程如圖10所示。

加密詳細過程：

1）混沌密碼發(fā)生器。借助新混沌系統(tǒng)生成6個M×N維的偽隨機矩陣。記密鑰為K={x0，y0，z0，r1，r2}，具體步驟：

第1步：由輸入密鑰K的前3個值作為新混沌系統(tǒng)的初始值，共迭代r1+r2+MN次，其中前r1+r2次是為了跳過系統(tǒng)的暫態(tài)。得到的3個偽隨機序列記作{xi}、{yi}、{zi}，i=1，2，…，MN。

2）明文敏感性分析。該性能測試方法為：借助密鑰K先后加密兩幅圖像P1和P2，其中P2從P1中隨機選取一個像素點（i，j），將該像素點的值改變1得到。相應(yīng)的密文圖像分別記為C1和C2。計算C1和C2之間的NPCR（像素改變率）、UACI（歸一化平均變化強度）值。上述方法共重復(fù)100次。最后計算上述2個指標的平均值。

仿真時，明文和密文圖像分別選取2 000對相鄰的像素點。由表1中的相關(guān)系數(shù)計算結(jié)果與圖13的相鄰像素灰度值示意圖可得出結(jié)論：明文圖像在各個方向都具有很強的相關(guān)性，而密文圖像則無相關(guān)性。

3）密文敏感性分析。該性能測試方法與明文敏感性類似，不同在于，改變的不是明文圖像的像素點，而是密文圖像的像素點。并且需要用同一密鑰對兩個不同的密文圖像解密分別得到P1和P2，計算P1和P2之間的NPCR、UACI值。對“Cameraman”加密后的圖像，計算得NPCR=99.603 1%，UACI=31.173 9%，結(jié)果接近理論值，因此該加密方案具有較好的密文敏感性。

4）密鑰靈敏度。正確的解密結(jié)果應(yīng)如圖14 a所示。但進行解密操作時若取密鑰K={x0，y0，z0，r1，r2}={-1，-1，-1-10-15，35，201}，解密結(jié)果將如圖14 b所示。雖然密鑰僅有一個數(shù)值有10-15的偏差，但直觀上可以發(fā)現(xiàn)解密圖像仍然呈現(xiàn)噪聲形式，無法傳達有效信息。這表明該加密方案的密鑰靈敏度極優(yōu)。

5 結(jié)論

本文設(shè)計了一種含有三次多項式取絕對值函數(shù)的混沌系統(tǒng)。通過數(shù)值分析和MATLAB仿真分析了基本屬性和動力學(xué)特性。結(jié)果表明，雖然這一系統(tǒng)在一定的參數(shù)條件下僅有一個指標2的鞍焦平衡點，但存在混沌現(xiàn)象，且狀態(tài)變量初值對稱時存在共存吸引子或聚合吸引子。系統(tǒng)的某幾個參數(shù)或系統(tǒng)初值變化時，具有持續(xù)周期或混沌的動力學(xué)特性，也有調(diào)幅特性。電路仿真驗證了理論的正確性。最后基于新設(shè)計的混沌系統(tǒng)設(shè)計了加密方案，仿真與分析表明了加密方案的有效性。

參考文獻：

[1]LORENZ E N. Deterministic non-periodic flows [J]. Journal of the Atmospheric Sciences， 1963， 20（3）： 130－141.

[2]田興華， 張紀會， 李陽. 基于混沌映射的自適應(yīng)退火型粒子群算法 [J]. 復(fù)雜系統(tǒng)與復(fù)雜性科學(xué)， 2020， 17（1）： 45－54.

TIAN X H， ZHANG J H， LI Y. An adaptive annealing particle swarm optimization based on chaotic mapping [J]. ComplexSystems and Complexity Science， 2020， 17（1）： 45－54.

[3]LUO Y L， ZHOU R L， LIU J X， et al. A novel image encryption scheme based on Keplers third law and random Hadamard transform [J]. Chinese Physics B， 2017， 26（12）： 120504.

[4]SUN J W， YANG Q F， WANG Y F. Dynamical analysis of novel memristor chaotic system and DNA encryption application [J]. Iranian Journal of Science and Technology， Transactions of Electrical Engineering， 2020， 44： 449－460.

[5]劉林芳， 芮國勝， 張洋，等. 基于相空間對稱Lorenz陣子群的混沌通信保密研究 [J]. 通信學(xué)報， 2019， 40（5）： 32－38.

LIU L F， RUI G S， ZHANG Y， et al. Research on the chaotic secure communication of the phase-space symmetric Lorenz oscillator group [J]. Journal on Communications， 2019， 40（5）： 32－38.

[6]SAHIN M， TASJIRAN Z， HASAN G， et al. Application and modeling of a novel 4D memristive chaotic system for communication systems[J]. Circuits， Systems， and Signal Processing， 2020， 39： 3320－3349.

[7]YU F， LIU L， HE B Y， et al. Analysis and FPGA Realization of a novel 5D hyperchaotic four-wing memristive system， active control synchronization， and secure communication application [DB/OL].[2022-02-02].http：//doi.org/10.1155/2019/4047957.

[8]盧輝斌， 王麗佳. 基于Hopfield網(wǎng)絡(luò)的彩色圖像混沌加密算法 [J]. 吉林大學(xué)學(xué)報（信息科學(xué)版）， 2014， 32（2）： 131－137.

LU H B， WANG L J. Color image encryption algorithm of chaotic based on the hopfield network [J]. Journal of Jilin University （Information Science Edition）， 2014， 32（2）： 131－137.

[9]LIN H R， WANG C H， TAN Y M， et al. Hidden extreme multistability with hyperchaos and transient chaos in a Hopfield neural network affected by electromagnetic radiation [J]. Nonlinear Dynamics， 2020， 99： 2369－2386.

[10] 孫亮， 羅佳， 喬印虎.局部有源憶阻器電路及其在HR耦合神經(jīng)元網(wǎng)絡(luò)中的應(yīng)用[J].電子與信息學(xué)報，2021，43（11）： 3374－3383.

SUN L， LUO J， QIAO Y H. A Locally active memristor circuit and its application to a coupled hindmarsh-rose neuron network [J]. Journal of Electronics & Information Technology， 2021， 43（11）： 3374－3383.

[11] 師東生， 石煒. 一個新四翼高維超混沌系統(tǒng)的復(fù)雜動力學(xué)行為研究與仿真 [J]. 現(xiàn)代電子技術(shù)， 2020， 43（19）： 10－13.

SHI D S， SHI W. Research and simulation of complex dynamic behavior of new four-wing high-dimensional hyperchaotic system [J]. Modern Electronics Technique， 2020， 43（19）： 10－13.

[12] 鮮永菊， 扶坤榮， 徐昌彪. 一個具有多翼吸引子的四維多穩(wěn)態(tài)超混沌系統(tǒng) [J]. 振動與沖擊， 2020， 40（1）： 15－22， 38.

XIAN Y J， FU K R， XU C B. A 4-D multi-stable hyper-chaotic system with multi-wing attractors [J]. Journal of Vibration and Shock， 2020， 40 （1）： 15－22， 38.

[13] YANG L B， YANG Q G， CHEN G R. Hidden attractors， singularly degenerate heteroclinic orbits， multistability and physical realization of a new 6D hyperchaotic system [J]. Communications in Nonlinear Science and Numerical Simulation， 2020， 90： 105362.

[14] MA J， CHEN Z Q， WANG Z L， et al. A four-wing hyper-chaotic attractor generated from a 4-D memristive system with a line equilibrium [J]. Nonlinear Dynamics， 2015， 81： 1275－1288.

[15] QI G Y， CHEN G R， DU S Z， et al. Analysis of a new chaotic system [J]. Physica A， 2005， 352： 295－308.

[16] ATIYEH B， KARTHIKEYAN R， ABDUL J， et al. Dynamical analysis of a new multistable chaotic system with hidden attractor： antimonotonicity， coexisting multiple attractors， and offset boosting [J]. Physics Letters A， 2019， 383： 1450－1456.

[17] BAO H， WANG N， BAO B C， et al. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria [J]. Communications in Nonlinear Science and Numerical Simulation， 2018， 57： 264－275.

[18] CHEN Q F， HONG Y G， CHEN G R. Chaotic behaviors and toroidal/spherical attractors generated by discontinuous dynamics[J]. Physica A， 2006， 371： 293－302.

[19] 臧鴻雁， 韋心元， 袁悅. 一類三次多項式混沌映射的判定及性能分析 [J]. 電子與信息學(xué)報， 2021， 43（2）： 454－460.

ZANG H Y， WEI X Y， YUAN Y. Determination and properties analysis of a cubic polynomial chaotic map [J]. Journal of Electronics & Information Technology， 2021， 43（2）： 454－460.

[20] 高秉建. 基于Liu混沌系統(tǒng)生成的多翅膀蝴蝶吸引子 [J]. 復(fù)雜系統(tǒng)與復(fù)雜性科學(xué)， 2016， 13（1）： 91－94.

GAO B J. Multi-wing butterfly attractor from a modified chaotic system [J].Complex Systems and Complexity Science， 2016， 13（1）： 91－94.

[21] WANG Z， SUN C， JIN F， et al. A widely amplitude-adjustable chaotic oscillator based on a physical model of HP memristor [J]. IEICE Electronics Express， 2018， 15（8）： 1－6.

[22] WANG R， LI C B， CICEK S， et al. Amemristive hyperjerk chaotic system： amplitude control， FPGA design， and prediction with artificial neural network [DB/OL].[2022-02-01].http：//doi.org/10.1155/2021/6636813.

（責任編輯 李 進）

收稿日期：2022－05－18；修回日期：2022－07－08

基金項目： 中國博士后科學(xué)基金（2015T80279）；山東省自然科學(xué)基金（ZR2020MF071）

第一作者： 高正中（1971－），男，山東濟寧人，博士，教授，主要研究方向為計算機檢測與控制、機器人技術(shù)等。