具有稚蟲(chóng)遷徙機(jī)制的S型自適應(yīng)混沌蜉蝣算法

張恒齊 錢(qián)謙

基金項(xiàng)目：云南省科技廳基礎(chǔ)研究專項(xiàng)（批準(zhǔn)號(hào)：202101AT070082）資助的課題。

作者簡(jiǎn)介：張恒齊（1994-），碩士研究生，從事計(jì)算智能、智能信息處理等的研究。

通訊作者：錢(qián)謙（1981-），副教授，從事計(jì)算智能與視覺(jué)認(rèn)知的研究，Qianqian_yn@126.com。

引用本文：張恒齊，錢(qián)謙.具有稚蟲(chóng)遷徙機(jī)制的S型自適應(yīng)混沌蜉蝣算法［J］.化工自動(dòng)化及儀表，2024，51（2）：262-273.

DOI：10.20030/j.cnki.1000-3932.202402016

摘 要 針對(duì)蜉蝣優(yōu)化算法（MA）全局搜索能力較弱，對(duì)子代優(yōu)秀個(gè)體有效信息利用不夠充分的缺點(diǎn)，以及在計(jì)算中后期易陷入局部收斂，進(jìn)而影響優(yōu)化效果的問(wèn)題，提出一種具有稚蟲(chóng)遷徙機(jī)制的S型自適應(yīng)混沌蜉蝣優(yōu)化算法（S-AMA）。S-AMA算法首先采用Logistic混沌映射產(chǎn)生蜉蝣種群，增加算法初期種群的多樣性；隨后，將蜉蝣生命周期進(jìn)行數(shù)學(xué)建模，并引入S型生命系數(shù)替換原有的重力慣性系數(shù)，動(dòng)態(tài)調(diào)整算法探索能力和開(kāi)發(fā)能力間的平衡性；最后，根據(jù)蜉蝣在缺氧環(huán)境下的種群活動(dòng)，引入稚蟲(chóng)遷徙機(jī)制強(qiáng)化子代優(yōu)秀個(gè)體擺脫局部最優(yōu)的能力，進(jìn)而更加充分地搜索最優(yōu)解附近的區(qū)域，以增強(qiáng)算法的收斂精度。實(shí)驗(yàn)部分將S-AMA應(yīng)用于標(biāo)準(zhǔn)函數(shù)測(cè)試集，并分別進(jìn)行優(yōu)化對(duì)比實(shí)驗(yàn)、Wilcoxon秩和檢驗(yàn)。結(jié)果表明：與對(duì)比算法相比，S-AMA算法具有更好的尋優(yōu)能力、收斂速度及魯棒性。

關(guān)鍵詞 S型自適應(yīng)混沌蜉蝣優(yōu)化算法（S-AMA） 稚蟲(chóng)遷徙機(jī)制 混沌映射 S型生命系數(shù) 萊維飛行

中圖分類號(hào) TP18? 文獻(xiàn)標(biāo)志碼 A? ?文章編號(hào) 1000-3932（2024）02-0262-12

隨著科學(xué)技術(shù)的不斷創(chuàng)新發(fā)展，工程問(wèn)題［1］實(shí)例的規(guī)模越來(lái)越大，相關(guān)問(wèn)題計(jì)算的時(shí)間和空間復(fù)雜度呈指數(shù)上升。傳統(tǒng)優(yōu)化算法（如梯度下降［2］、牛頓法［3］）依賴于目標(biāo)函數(shù)連續(xù)或可導(dǎo)，無(wú)法滿足現(xiàn)實(shí)中具有復(fù)雜數(shù)學(xué)特性優(yōu)化問(wèn)題的求解需求。元啟發(fā)式算法（Metaheuristic Algorithms，MAs）因不依賴于目標(biāo)問(wèn)題的梯度信息，易于布署，已被應(yīng)用于動(dòng)態(tài)網(wǎng)絡(luò)社區(qū)發(fā)現(xiàn)［4］、路徑規(guī)劃［5］、線性天線陣列的模式合成優(yōu)化［6］及集成風(fēng)速預(yù)測(cè)系統(tǒng)［7］等領(lǐng)域。MAs大多是對(duì)自然界的生物行為學(xué)習(xí)研究后獲得靈感啟發(fā)而得，常見(jiàn)算法有粒子群算法（Particle Swarm Optimization，PSO）［8］、蜉蝣優(yōu)化算法（Mayfly Algorithm，MA）［9］、哈里斯鷹優(yōu)化算法（Harris Hawk Optimization，HHO）［10］、黏菌優(yōu)化算法（Slime Mould Algorithm，SMA）［11］、灰狼優(yōu)化算法（Grey Wolf Optimization，GWO）［12］等。但MAs存在一些缺陷，如收斂精度低、易陷入局部最優(yōu)等，影響了算法的優(yōu)化性能。NFL（No Free Lunch）理論同樣指出不存在某種單一優(yōu)化算法能夠同時(shí)處理所有的工程問(wèn)題［13］。因此，需要對(duì)傳統(tǒng)元啟發(fā)式算法進(jìn)行改進(jìn)，以優(yōu)化其性能。

蜉蝣算法（Mayfly Algorithm，MA）是希臘學(xué)者Konstantinos Zervoudakis等受蜉蝣生物活動(dòng)啟發(fā)而提出的一種新型元啟發(fā)式優(yōu)化算法，用于解決復(fù)雜函數(shù)優(yōu)化問(wèn)題。迄今為止，MA已被應(yīng)用于動(dòng)態(tài)網(wǎng)絡(luò)社區(qū)發(fā)現(xiàn)［4］、線性天線陣列的模式合成優(yōu)化［6］、集成風(fēng)速預(yù)測(cè)形態(tài)［7］等。說(shuō)明MA相比于其他傳統(tǒng)算法的求解精度高、收斂快，在工程領(lǐng)域受到學(xué)者們的青睞。但MA與其他群智能算法一樣，搜索精度和收斂速度有待優(yōu)化。因此，學(xué)者們對(duì)MA進(jìn)行了改進(jìn)，文獻(xiàn)［14］提出一種基于Logistic映射的蜉蝣優(yōu)化算法（LMA），通過(guò)Logistic映射對(duì)優(yōu)秀蜉蝣進(jìn)行擾動(dòng)來(lái)防止種群出現(xiàn)早熟收斂現(xiàn)象；文獻(xiàn)［15］提出了一種基于倒位變異的蜉蝣優(yōu)化算法（IVMA），將倒位變異與突變結(jié)合，提高了算法在求解高維復(fù)雜問(wèn)題時(shí)的收斂精度；文獻(xiàn)［16］提出一種基于黃金正弦自適應(yīng)融合的蜉蝣優(yōu)化算法，通過(guò)引入黃金正弦因子和萊維飛行策略平衡了算法的全局搜索行為與局部搜索行為；文獻(xiàn)［17］提出一種偏移進(jìn)化蜉蝣優(yōu)化算法，引入拉伸因子，通過(guò)偏移進(jìn)化機(jī)制增強(qiáng)了算法的收斂性能；文獻(xiàn)［18］提出一種增強(qiáng)全局搜索和自適應(yīng)的蜉蝣算法，算法主要引入不完全伽瑪函數(shù)與Beta累加分布的自適應(yīng)的慣性權(quán)重平衡了算法的全局搜索與開(kāi)發(fā)能力。上述文獻(xiàn)所提方法在一定程度上提升了算法的性能，但是大多只是簡(jiǎn)單的策略或算法上的疊加。

如果將蜉蝣的優(yōu)秀程度定義為根據(jù)問(wèn)題模型求得的適應(yīng)度值，則每個(gè)蜉蝣在搜索空間內(nèi)的位置代表目標(biāo)問(wèn)題的一個(gè)潛在解決方案。雖然MA具有較好的局部搜索能力并能保持一定的種群多樣性，但MA前期全局搜索能力較弱，導(dǎo)致算法后期的收斂精度較低，易陷入局部極值［9］。此外，MA迭代前期慣性系數(shù)較小，影響了蜉蝣種群的進(jìn)化效率，具體地說(shuō)，隨著婚禮舞蹈系數(shù)和飛行系數(shù)的數(shù)值隨迭代次數(shù)降低，算法后期的搜索步長(zhǎng)越來(lái)越小，使種群難以跳出局部最優(yōu)。為克服上述缺陷，增強(qiáng)種群的搜索效率，筆者提出一種具有稚蟲(chóng)遷徙機(jī)制的S型自適應(yīng)混沌蜉蝣優(yōu)化算法（S-type Adaptive Mayfly Algorithm Based on Larval Migration Mechanism，S-AMA）：

a. 種群初始化時(shí)加入Logistic混沌映射，以使種群位置分布更加均勻，同時(shí)保留一定隨機(jī)性，以增加種群多樣性，進(jìn)而保證算法初始狀態(tài)的搜索范圍；

b. 模擬蜉蝣的生命周期，提出一種S型生命系數(shù)非線性參數(shù)控制策略平衡算法的探索與開(kāi)發(fā)能力，以使算法能夠擁有更快的收斂速度以及更好的收斂精度；

c. 針對(duì)蜉蝣稚蟲(chóng)能夠在缺氧環(huán)境中尋找氧氣充沛棲息地的能力，在蜉蝣交配行為產(chǎn)生優(yōu)秀子代后加入稚蟲(chóng)遷徙機(jī)制，令子代蜉蝣能夠更好地跳出局部最優(yōu)，使其在后續(xù)搜索時(shí)更好地趨向于目標(biāo)問(wèn)題的最優(yōu)解。

最后，選用蜉蝣優(yōu)化算法（MA）［9］、粒子群算法（PSO）［8］、基于倒位變異的蜉蝣優(yōu)化算法（IVMA）［15］、基于Logistic映射的蜉蝣優(yōu)化算法（LMA）［14］、哈里斯鷹優(yōu)化算法（HHO）［10］、灰狼優(yōu)化算法（GWO）［12］等與S-AMA算法作對(duì)比，通過(guò)23個(gè)基準(zhǔn)測(cè)試函數(shù)進(jìn)行綜合性能比較，來(lái)驗(yàn)證算法的有效性和優(yōu)越性。

1 MA算法

MA算法的工作原理是：首先隨機(jī)生成雄性蜉蝣和雌性蜉蝣兩組種群作為算法的搜索代理群體，每個(gè)蜉蝣作為候選解被隨機(jī)置放在問(wèn)題空間中，用d維向量x=（x，x，…，x）表示，其優(yōu)劣程度由問(wèn)題模型的適應(yīng)度函數(shù)f（x）評(píng)估。而蜉蝣位置變化的度量用速度v=（v，v，…，v）表示，每只蜉蝣的飛行方向由個(gè)體經(jīng)驗(yàn)和社會(huì)經(jīng)驗(yàn)共同決定，并且每只蜉蝣都會(huì)調(diào)整自己的運(yùn)動(dòng)軌跡，使其能夠達(dá)到目前個(gè)人最佳位置pbest以及當(dāng)前所有蜉蝣所達(dá)到的最佳位置gbest。

1.1 雄性蜉蝣運(yùn)動(dòng)

求偶天性促使所有雄性蜉蝣聚集在一起，意味著每只雄性蜉蝣的位置都會(huì)根據(jù)自己和周?chē)従拥慕?jīng)驗(yàn)進(jìn)行調(diào)整。設(shè)x表示蜉蝣i在第t代的迭代中第j維的位置，那么其下一代位置x由當(dāng)前位置與速度共同決定：

x=x+v，x∈（x，x）? ? ?（1）

其中，x為初始化后位于第j維的雄性蜉蝣i；x與x分別為雄性蜉蝣位置變化區(qū)域的最大值與最小值。

雄性蜉蝣的聚集行為會(huì)使它們總是在離水面幾米的地方表演婚禮舞蹈，也意味著其飛行速度不會(huì)特別快。雄性蜉蝣i的飛行速度v的計(jì)算式為：

v=v+ae（pbest-x）+ae（gbest-x），f（x）>f（gbest）v+Dance·r? ? ? ? ? ? ，f（x）≤f（gbest）（2）

其中，v是蜉蝣i的第j維在第t代的速度；a，a是正吸引常數(shù)，分別用于衡量個(gè)體認(rèn)知和社會(huì)認(rèn)知；β是可見(jiàn)性系數(shù)，其取值為常數(shù)2，用來(lái)表達(dá)對(duì)其他蜉蝣的能見(jiàn)度；r是x和pbest的笛卡爾距離；pbest為蜉蝣i曾經(jīng)到過(guò)的最好位置；r為x和gbest的笛卡爾距離；gbest為當(dāng)前全局最佳位置；Dance是婚禮舞蹈系數(shù)；r是［-1，1］范圍內(nèi)的隨機(jī)數(shù)。

蜉蝣的優(yōu)秀程度定義為根據(jù)問(wèn)題模型求得的適應(yīng)度值，非優(yōu)秀雄性蜉蝣按式（2）第1行公式更新速度，優(yōu)秀雄性蜉蝣按式（2）第2行公式進(jìn)行舞蹈行為吸引雌性蜉蝣產(chǎn)生后代來(lái)保存自身的有效信息。

笛卡爾距離計(jì)算式為：

‖x′-X‖=? ? （3）

其中，x′代表雄性蜉蝣i；X可指代pbest或gbest；n為蜉蝣種群的維度上限；X只在式（3）中表示雌性蜉蝣的位置。

1.2 雌性蜉蝣運(yùn)動(dòng)

雌性蜉蝣的運(yùn)動(dòng)行為與雄性并不相同，它們不成群結(jié)隊(duì)，而是與雄性繁殖產(chǎn)生子代個(gè)體。設(shè)y是第t代的雌性蜉蝣i在第j維搜索空間中的位置，其位置更新公式如下：

y=y+v，y∈（y，y）? ? ?（4）

其中，y為初始化后位于j維的雌性蜉蝣i；y與y分別為雌性蜉蝣位置變化區(qū)域的最小值與最大值。

雌雄蜉蝣的良性結(jié)合更有助于種群的發(fā)展，優(yōu)秀的雄性蜉蝣應(yīng)該與優(yōu)秀的雌性蜉蝣結(jié)合交配，因此算法根據(jù)適應(yīng)度值對(duì)蜉蝣進(jìn)行排序與配對(duì)，其數(shù)學(xué)模型為：

v=v+ae（x-y），f（y）>f（x′）v+fl·r，f（y）≤f（x′） （5）

其中，r為雌雄蜉蝣的笛卡爾距離；fl是一個(gè)隨機(jī)的游動(dòng)系數(shù)，當(dāng)雄性比雌性優(yōu)秀時(shí)，雌性的速度按式（5）第1行公式更新，當(dāng)雌性不被雄性吸引時(shí)按式（5）第2行公式隨機(jī)游動(dòng)。

1.3 蜉蝣的交配

蜉蝣種群的發(fā)展與繁衍需要交配行為，交叉算子實(shí)現(xiàn)了雌雄蜉蝣之間的交配過(guò)程，具體地說(shuō)，分別從雄性種群和雌性種群中按適應(yīng)度選出父母樣本，然后按式（6）、（7）交配產(chǎn)生后代：

Offspring=L·male+（1-L）·female? ? （6）

Offspring=（1-L）·female+L·male? ? （7）

其中，Offspring、Offspring分別為交叉產(chǎn)生的兩個(gè)子代蜉蝣；L為［0，1］范圍內(nèi)的隨機(jī)值；male為父本位置向量；female為母本位置向量。后代的初速度值設(shè)定為零。

MA算法引入高斯變異［19］，對(duì)子代蜉蝣的單個(gè)維度進(jìn)行變異操作。子代蜉蝣的變異個(gè)數(shù)以種群數(shù)量Pop為基數(shù)，定義變異概率為mu，Pop·mu為種群中子代的變異個(gè)數(shù)。變異公式如下：

Offspring=Offspring+σ·N（0，1）? ?（8）

其中，Offspring為變異蜉蝣的第n個(gè)維度，其中n的取值為0～Pop·mu；σ為正態(tài)分布的標(biāo)準(zhǔn)差；N（0，1）為平均值為0、方差為1的標(biāo)準(zhǔn)正態(tài)分布隨機(jī)數(shù)。

2 S-AMA的改進(jìn)思想

由于蜉蝣算法的全局搜索能力較弱，交配后產(chǎn)生的優(yōu)秀子代蜉蝣直接進(jìn)行下一代的迭代，對(duì)子代優(yōu)秀個(gè)體有效信息的利用不夠充分，導(dǎo)致算法在計(jì)算中后期易陷入局部收斂，影響了算法的優(yōu)化效果。為了克服上述缺陷，筆者提出S-AMA算法，著重加強(qiáng)種群的全局搜索能力，并在算法后期的優(yōu)秀子代蜉蝣中加入稚蟲(chóng)遷徙機(jī)制，利用稚蟲(chóng)尋找富氧棲息地的能力跳出局部極值，避免了算法早熟收斂。

2.1 基于Logistic混沌映射的初始化方法

混沌序列具有內(nèi)隨機(jī)性、遍歷性、規(guī)律性等特點(diǎn)，看似混亂卻有著精致的內(nèi)在結(jié)構(gòu)，由混沌序列搜索得到的初始群體在一定程度上能夠提高算法的搜索效率［20］，增加種群多樣性。種群多樣性是元啟發(fā)式算法尋得最優(yōu)解的基本前提。混沌序列的生成方式主要有5種混沌映射［21］：Logistic映射、Henon映射、Tent映射、Lorenz映射、逐段線性混沌映射。由于Logistic映射從數(shù)學(xué)形式上是一個(gè)相對(duì)簡(jiǎn)單的映射方法，且其混沌系統(tǒng)具有不錯(cuò)的安全性，因此經(jīng)常被用作設(shè)計(jì)混沌流密碼系統(tǒng)。綜上所述，S-AMA利用Logistic混沌映射的數(shù)學(xué)特性產(chǎn)生初始種群，可使初始種群在解空間內(nèi)分布得更加均勻、隨機(jī)，有助于提升算法的種群多樣性，而初始種群的豐富有利于算法更加全面地探索，提高最終優(yōu)化解的精度。具體而言，筆者提出的初始化方法可以使初始種群在解空間內(nèi)分布的點(diǎn)位更加均勻、隨機(jī)，算法基于映射后的點(diǎn)位能夠更加充分地探索最優(yōu)解。Logistic混沌映射的數(shù)學(xué)公式為：

z=μ·z（1-z），μ∈［0，4］，z∈［0，1］? ?（9）

其中，z為第n+1代蜉蝣i的混沌映射位置；μ為分支參數(shù)，通常取4；z為第n代蜉蝣i的混沌映射位置。

把式（9）中的z代入式（10）可得種群初始化計(jì)算式：

x=x+z（x-x）? ? （10）

其中，x為初始化過(guò)程中的第i個(gè)蜉蝣的位置。

2.2 基于S型生命系數(shù)的自適應(yīng)慣性權(quán)重系數(shù)

文獻(xiàn)［9］提出一種對(duì)基礎(chǔ)蜉蝣算法的改進(jìn)方法，加入了重力系數(shù)因子g（相當(dāng)于一種慣性權(quán)重因子），在算法的搜索與開(kāi)發(fā)能力上具有平衡與指導(dǎo)的作用。

雄性蜉蝣的速度更新公式如下：

v=g·v+ae（pbest-x）+ae（gbest-x），f（x）>f（gbest）g·v+Dance·r? ? ? ? ? ，f（x）≤f（gbest）

（11）

雌性蜉蝣的速度更新公式如下：

v=g·v+ae（x-y），f（y）>f（x）g·v+fl·r? ? ，f（y）≤f（x）? （12）

當(dāng)慣性系數(shù)較大時(shí)算法探索能力較強(qiáng)，而當(dāng)慣性系數(shù)較小時(shí)算法的開(kāi)發(fā)能力較強(qiáng)［22］。MA的重力系數(shù)權(quán)重隨著算法迭代逐漸呈線性減少，沒(méi)有針對(duì)性地對(duì)種群前期的探索進(jìn)行著重處理，也沒(méi)有對(duì)后期的開(kāi)發(fā)進(jìn)行適應(yīng)調(diào)整，影響了算法的搜索性能。

本研究將S型生命系數(shù)看作蜉蝣的生命能量，前半生青壯年蜉蝣的精力充沛能夠飛行到更廣泛的區(qū)域進(jìn)行全局搜索，到了后半生暮年之際具有豐富的經(jīng)驗(yàn)?zāi)軌蚋泳珳?zhǔn)地進(jìn)行局部搜索。如圖1所示，如果把慣性權(quán)重因子看作蜉蝣的生命能量，S型生命系數(shù)可以使算法在迭代前期具有較大的慣性系數(shù)，更好地進(jìn)行全局搜索；而在迭代后期急速下降并保持一個(gè)較小的值，使算法傾向于局部搜索。筆者提出的S型生命系數(shù)可以很好地平衡算法的全局搜索能力與局部搜索能力，滿足算法各個(gè)階段的需求［23］。Sigmoid函數(shù)是基礎(chǔ)的S型激活函數(shù)，故在此引入的S型生命曲線為Sigmoid函數(shù)（圖1）。

圖1 符合S型生命曲線函數(shù)

第t代的生命曲線系數(shù)ω的計(jì)算式為：

ω=ω+（ω+ω）/（1+exp（-（2S·（T-t）/T-S）））（13）

其中，ω與ω為慣性權(quán)重的最大值與最小值，分別為0.8與0.2；T為最大迭代次數(shù)；t為當(dāng)前的迭代次數(shù)。本研究選取［S，S］范圍內(nèi)S型生命曲線的自適應(yīng)系數(shù)函數(shù)，其中S為10，S為-10。

綜上所述，帶有S型生命曲線自適應(yīng)系數(shù)的雄性蜉蝣的位置更新公式如下：

v=ω·v+ae（pbest-x）+ae（gbest-x），f（x）>f（gbest）ω·v+d·r? ? ? ? ? ? ，f（x）≤f（gbest）

（14）

帶有S型生命曲線自適應(yīng)系數(shù)的雌性蜉蝣的位置更新公式如下：

v=ω·v+ae（x-y），f（y）>f（x）ω·v+fl·r? ? ，f（y）≤f（x）? （15）

2.3 蜉蝣的稚蟲(chóng)遷徙機(jī)制

蜉蝣稚蟲(chóng)在生長(zhǎng)發(fā)育過(guò)程中，要不斷蛻皮，并且稚蟲(chóng)在缺氧條件下能夠移動(dòng)到更多氧環(huán)境的棲息地生活。在此現(xiàn)象啟發(fā)下，本研究利用父母蜉蝣交配產(chǎn)生基因優(yōu)秀的子代蜉蝣，根據(jù)優(yōu)秀子代蜉蝣在稚蟲(chóng)期尋氧遷徙活動(dòng)，自主地從缺氧環(huán)境遷移到氧氣充沛的環(huán)境中，尋找更適宜的棲息地。S-AMA稚蟲(chóng)遷徙公式如下：

OffSpring=OffSpring+m·（Levy·gbest-OffSpring） （16）

其中，OffSpring為第t代的稚蟲(chóng)i的位置；m為遷徙系數(shù)，控制種群四處尋找有氧環(huán)境的能力，取［0，1］范圍內(nèi)的隨機(jī)數(shù)；Levy為萊維飛行；gbest為目前蜉蝣所能到達(dá)的最優(yōu)位置，即當(dāng)前全局最優(yōu)位置，因?yàn)椴还馐侵上x(chóng)遷徙機(jī)制在更新位置，還有雌雄蜉蝣各自在更新位置，所以只說(shuō)稚蟲(chóng)尋到氧氣最充沛的位置不全面。

稚蟲(chóng)通過(guò)向氧氣充沛的地方靠近，來(lái)尋找更加合適的棲息地。萊維飛行能夠增加稚蟲(chóng)群體遷徙的范圍，使其能在目前最適合的位置周?chē)鷶_動(dòng)，增加尋找到最優(yōu)棲息地的概率。通過(guò)式（16）的應(yīng)用，子代能夠進(jìn)一步提升自己的優(yōu)秀度，增加尋優(yōu)精度，提高跳出局部最優(yōu)的可能性。

萊維飛行是模擬自然界中一種鳥(niǎo)類飛行的運(yùn)動(dòng)，它和隨機(jī)游走的布朗運(yùn)動(dòng)不同，擁有小概率大步伐、大概率小步伐的特征，能夠使種群在后期進(jìn)化中既擁有較好的局部尋優(yōu)能力又同時(shí)擁有強(qiáng)力跳出局部最優(yōu)值的能力［24］。萊維飛行的運(yùn)動(dòng)可表示為：

Levy=γ·? ? ?（17）

σ=（18）

其中，γ為萊維飛行的飛行尺度；u，v是（0，1）內(nèi)的隨機(jī)值；β′是萊維飛行中的默認(rèn)常數(shù)，設(shè)置為1.5；J（）為伽瑪函數(shù)；σ為標(biāo)準(zhǔn)差。

2.4 算法時(shí)間復(fù)雜度分析

對(duì)于MA算法來(lái)說(shuō)，設(shè)搜索空間維度為D，雄性蜉蝣數(shù)量為N，雌性蜉蝣數(shù)量為N，子代蜉蝣交配數(shù)量為N，交配過(guò)程的復(fù)雜度記為O（N）。最大迭代次數(shù)為T(mén)。初始化過(guò)程的復(fù)雜度為O（1），標(biāo)準(zhǔn)MA的時(shí)間復(fù)雜度T（n）=O（1+T（ND+ND+ND））。

S-AMA增加了混沌初始化、S型生命系數(shù)自適應(yīng)慣性權(quán)重和稚蟲(chóng)遷徙機(jī)制。混沌初始化與S型生命系數(shù)自適應(yīng)慣性權(quán)重都分別嵌入在初始化與速度更新公式中，所以復(fù)雜度都為O（1），加入稚蟲(chóng)遷徙機(jī)制，增加了對(duì)子代蜉蝣的進(jìn)化公式，使其進(jìn)行迭代更新，其復(fù)雜度為O（N）。則過(guò)濾低次項(xiàng)后改進(jìn)的算法時(shí)間復(fù)雜度為 T（n）=O（1+T （N D+N D+N （D+1）），可以看出，算法改進(jìn)后，并未明顯提升時(shí)間復(fù)雜度。

3 實(shí)驗(yàn)分析與性能評(píng)估

為了驗(yàn)證S-AMA算法的性能，采用標(biāo)準(zhǔn)測(cè)試函數(shù)進(jìn)行實(shí)驗(yàn)。實(shí)驗(yàn)環(huán)境采用Intel（R）Core（TM）I5-10th CPU，內(nèi)存8 GB，操作系統(tǒng)為64位WIN11計(jì)算機(jī)。編程語(yǔ)言MATLAB（R2020b）。使用23個(gè)標(biāo)準(zhǔn)測(cè)試函數(shù)［25］對(duì)S-AMA進(jìn)行性能測(cè)試，詳見(jiàn)表1，在這些函數(shù)中，F(xiàn)1～F7為單峰函數(shù)，僅有一個(gè)全局最優(yōu)解，用來(lái)測(cè)試算法的局部開(kāi)發(fā)能力和收斂速度；F8～F13為多維度多峰函數(shù)，具有多個(gè)局部最優(yōu)值和一個(gè)全局最優(yōu)值，用來(lái)測(cè)試算法的全局搜索能力與跳出局部最優(yōu)的能力；F14～F23為固定維數(shù)的多峰測(cè)試函數(shù)，用來(lái)檢測(cè)算法平衡探索與開(kāi)發(fā)能力之間的性能。

3.1 對(duì)比算法與參數(shù)設(shè)置

本次選擇6種算法進(jìn)行對(duì)比，其中有針對(duì)MA的最新改進(jìn)算法IVMA［14］、LMA［13］，性能較為優(yōu)秀并且較新的群?jiǎn)l(fā)式算法HHO［6］、GWO［8］，以及傳統(tǒng)群優(yōu)化算法PSO［4］。為了更加直觀有效地對(duì)比各算法的優(yōu)劣，設(shè)定參數(shù)盡量統(tǒng)一，種群規(guī)模N=50，維度D=30，最大迭代次數(shù)Tmax=500，其他參數(shù)設(shè)置見(jiàn)表2。各算法獨(dú)立運(yùn)行30次，選取平均值、標(biāo)準(zhǔn)差、最優(yōu)值、Wilcoxon秩和檢驗(yàn)作為評(píng)價(jià)標(biāo)準(zhǔn)，其中平均值與標(biāo)準(zhǔn)差越小算法性能和穩(wěn)定性越佳。

3.2 求解精度分析

S-AMA及對(duì)比算法的實(shí)驗(yàn)結(jié)果見(jiàn)表3，其中Best為最優(yōu)適應(yīng)度值、Mean為平均值、Std為標(biāo)準(zhǔn)差，紅色數(shù)據(jù)是最佳實(shí)驗(yàn)結(jié)果。F1～F7為單峰函數(shù)。可以看到S-AMA在F1～F4中都能達(dá)到最好的尋優(yōu)結(jié)果以及尋優(yōu)精度，在F5～F7中尋優(yōu)結(jié)果也位于前三；在F8～F13的多峰函數(shù)中，S-AMA在大多數(shù)情況下都找到了最優(yōu)值，僅在F10中穩(wěn)定性稍弱于HHO，但也尋到了最優(yōu)值，可見(jiàn)S-AMA具有優(yōu)秀的跳出局部最優(yōu)能力和探索能力，整體效果最優(yōu)。對(duì)于其他多峰固定維度函數(shù)，除了函數(shù)F23的標(biāo)準(zhǔn)差沒(méi)有達(dá)到最優(yōu)，其余皆為最優(yōu)，充分說(shuō)明S-AMA算法具有突出的平衡探索與開(kāi)發(fā)能力，能在尋到最優(yōu)的基礎(chǔ)上保持最佳的穩(wěn)定性。

3.3 收斂曲線分析

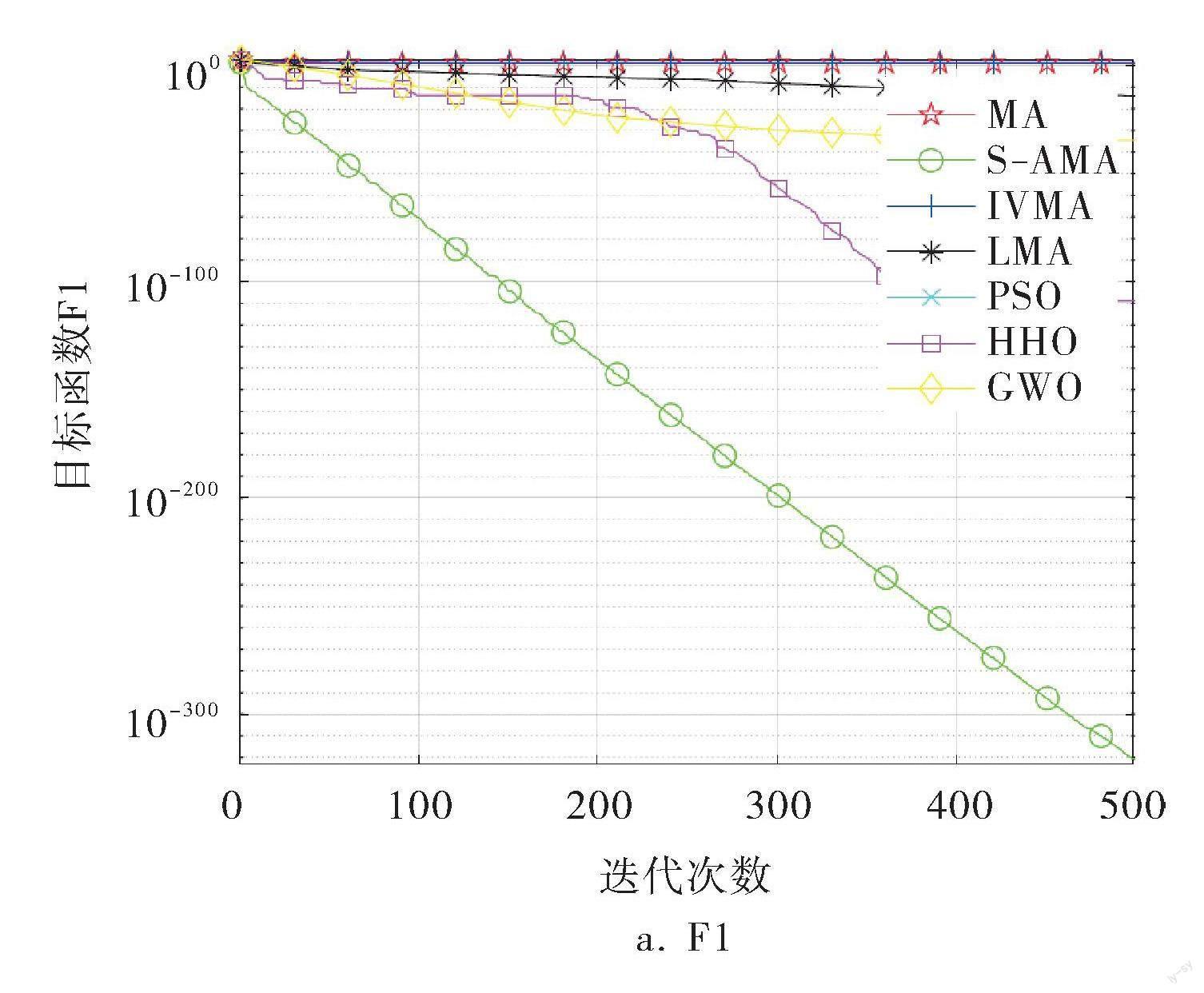
各種算法的部分函數(shù)收斂曲線如圖2所示，從中可以更加直觀地看出差異性。在單峰測(cè)試函數(shù)F1～F4中，可以看到S-AMA的尋優(yōu)精度遠(yuǎn)遠(yuǎn)強(qiáng)于其他所有算法，僅在F3中，S-AMA在中期收斂略慢于HHO，但到迭代后期，收斂精度遠(yuǎn)優(yōu)于HHO；而在多峰測(cè)試函數(shù)F8～F11中可以看到，S-AMA能夠以極快的速度收斂到最優(yōu)值，遠(yuǎn)遠(yuǎn)超出其他函數(shù)的效率，僅在F10中，尋優(yōu)精度略遜于HHO；而在F13中，也是在后期擁有了最好的尋優(yōu)精度。通過(guò)圖像收斂曲線（圖2）可以看到，S-AMA的初期收斂速度遠(yuǎn)勝于其他算法，說(shuō)明引入的混沌映射產(chǎn)生的種群多樣性對(duì)于算法的前期探索奠定了良好的種群基礎(chǔ)；到了后期，曲線持續(xù)下滑，則是由于引入的S型生命曲線以及稚蟲(chóng)遷徙機(jī)制發(fā)揮了不錯(cuò)的效果。從收斂曲線分析可知，3種改進(jìn)策略對(duì)算法的優(yōu)化都有不錯(cuò)的效果。

圖2 各種算法的部分函數(shù)收斂曲線

綜上所述，S-AMA在尋優(yōu)速率與尋優(yōu)精度上綜合強(qiáng)于其他算法。

3.4 Wilcoxon秩和檢驗(yàn)

為了精確分析實(shí)驗(yàn)結(jié)果，采用Wilcoxon秩和檢驗(yàn)來(lái)檢驗(yàn)算法結(jié)果之間是否具有顯著性差別。秩和檢驗(yàn)在5%的顯著水平下進(jìn)行，當(dāng)檢測(cè)值p＜0.05時(shí)，可以證明兩種算法的性能存在著顯著差異，否則證明兩種算法的尋優(yōu)性能并沒(méi)有顯著差異。

將S-AMA算法與要對(duì)比的6種算法各自獨(dú)立運(yùn)行30次，參數(shù)種群個(gè)數(shù)N=30、維度D=30，測(cè)試23個(gè)標(biāo)準(zhǔn)測(cè)試函數(shù)判斷S-AMA與6種對(duì)比算法所得結(jié)果的顯著性區(qū)別。Wilcoxon統(tǒng)計(jì)的檢驗(yàn)值p見(jiàn)表4，其中，紅色數(shù)據(jù)表示算法間差異性較小，性能相當(dāng)；N/A表示數(shù)據(jù)無(wú)效，即實(shí)驗(yàn)樣本數(shù)據(jù)相同，算法性能相當(dāng)。根據(jù)p值判斷，當(dāng)p＜0.05時(shí)，說(shuō)明所對(duì)比的兩種算法有顯著性差異。表4中的紅色數(shù)據(jù)表示算法之間沒(méi)有顯著性差異，僅出現(xiàn)很少的次數(shù)，表明S-AMA與其余對(duì)比算法之間在絕大部分情況下均具有顯著性差異。

綜合分析表3、4和圖2可知，具有稚蟲(chóng)遷徙機(jī)制的自適應(yīng)混沌蜉蝣優(yōu)化算法（S-AMA）的全局和局部尋優(yōu)能力都得到加強(qiáng)，尋優(yōu)能力優(yōu)于MA以及IVMA、LMA和PSO，并且也優(yōu)于性能優(yōu)良的較為新穎的HHO、GWO。說(shuō)明S-AMA具有優(yōu)秀的收斂精度、收斂速度和魯棒性。

4 結(jié)束語(yǔ)

筆者提出一種具有稚蟲(chóng)遷徙機(jī)制的S型自適應(yīng)混沌蜉蝣優(yōu)化算法。改進(jìn)后的蜉蝣算法經(jīng)過(guò)標(biāo)準(zhǔn)函數(shù)的測(cè)試后，有效證明了其收斂速度和收斂精度有所提升。蜉蝣算法目前已經(jīng)能夠應(yīng)用到動(dòng)態(tài)網(wǎng)絡(luò)社區(qū)發(fā)現(xiàn)問(wèn)題，以及線性天線陣列的模式合成優(yōu)化等問(wèn)題中，算法整體性能的提升，可進(jìn)一步提高蜉蝣算法在工程優(yōu)化領(lǐng)域中應(yīng)用的可能性。然而算法性能的進(jìn)步總是伴隨著穩(wěn)定性的下降，改進(jìn)后的蜉蝣算法若想要真正融入且擴(kuò)散到各個(gè)領(lǐng)域，仍然需要研究在保證算法尋優(yōu)穩(wěn)定性的前提下提高算法整體的尋優(yōu)性能，盡可能降低其優(yōu)化誤差。因此，下一步的研究方向應(yīng)該使用不同的現(xiàn)實(shí)數(shù)據(jù)集來(lái)測(cè)試改進(jìn)的蜉蝣算法，繼續(xù)發(fā)現(xiàn)其優(yōu)缺點(diǎn)，逐步改進(jìn)，使其盡可能完善，并最終應(yīng)用到各領(lǐng)域中，發(fā)揮其價(jià)值。

參 考 文 獻(xiàn)

［1］ 張發(fā)展，賀毅朝，劉雪靜，等.新穎的離散差分演化算法求解D{0-1}KP問(wèn)題［J］.計(jì)算機(jī)科學(xué)與探索，2022，16（2）：468-479.

［2］ QIAN N.On the momentum term in gradient descent learning algorithms［J］.Neural Networks，1999，12（1）：145-151.

［3］ 孫秋野，陳會(huì)敏，楊家農(nóng)，等.牛頓類潮流計(jì)算方法的收斂性分析［J］.中國(guó)電機(jī)工程學(xué)報(bào)，2014，34（13）：2196-2200.

［4］ 李浩，楊海瀟，張?zhí)m，等.改進(jìn)離散蜉蝣算法的多目標(biāo)動(dòng)態(tài)網(wǎng)絡(luò)社區(qū)發(fā)現(xiàn)［J］.計(jì)算機(jī)科學(xué)與探索，2023，17（4）：942-952.

［5］ NAIK M K，PANDA R，ABRAHAM A.Normalized square difference based multilevel thresholding technique for multispectral images using leader slime mould algorithm［J/OL］.Journal of King Saud UniversityComputer and Information Sciences，［2021-02-04］.https：//doi.org/10.1016/j.jksuci.2020.10.030.html.

［6］ XIA K W，WANG T，ABUBAKAR U.Pattern Synthesis of Uniform and Sparse Linear Antenna Array Using Mayfly Algorithm［J］.IEEE Access，2021（9）：77954-77971.

［7］ LIU Z K，JING P，WANG J Z，et al.Ensemble forecasting system for short-term wind speed forecasting based on optimal sub-model selection and multi-objective version of mayfly optimization algorithm［J］.Expert Systems with Applications，2021，177：114974.

［8］ KENNEDY J，EBERHART R.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks.Piscataway，NJ：IEEE，1995：1942-1948.

［9］ ZERVOUDAKIS K，TSAFARAKIS S.A mayfly optimization algorithm［J］.Computers & Industrial Engineering，2020，145：106559-106577.

［10］ HEIDARI A A，MIRJALILI S，F(xiàn)ARIS H，et al.Harris hawks optimization：Algorithm and applications［J］.Future Generation Computer Systems，2019，97：849-872.

［11］ LI S M，CHEN H L，WANG M J，et al.Slime mould algorithm：A new method for stochastic optimization［J］.Future Generation Computer Systems，2020，111：300-323.

［12］ MIRJALILI S，MIRJALILI S M，LEWIS A.Grey wolf optimizer［J］.Advances in Engineering Software，2014，69：46-61.

［13］ OLPERT D H，MACREADY W G.No free lunch theorems for optimization［J］.IEEE Transactions on Evolutionary Computation，1997（1）：67-82.

［14］ 陳嘉豪，童楠，符強(qiáng).基于Logistic映射的蜉蝣優(yōu)化算法［J］.計(jì)算機(jī)時(shí)代，2021（10）：6-10.

［15］ 陳偉超，符強(qiáng).基于倒位變異的蜉蝣優(yōu)化算法［J］.計(jì)算機(jī)系統(tǒng)應(yīng)用，2021，30（8）：157-163.

［16］ 王義，張達(dá)敏.基于黃金正弦與自適應(yīng)融合的蜉蝣優(yōu)化算法［J］.計(jì)算機(jī)應(yīng)用研究，2021，38（10）：3072-3077.

［17］ 王克逸，符強(qiáng)，陳嘉豪.偏移進(jìn)化蜉蝣優(yōu)化算法［J］.計(jì)算機(jī)系統(tǒng)應(yīng)用，2022，31（3）：150-158.

［18］ 王義，張達(dá)敏，鄒誠(chéng)誠(chéng).增強(qiáng)全局搜索和自適應(yīng)蜉蝣算法［J］.哈爾濱工業(yè)大學(xué)學(xué)報(bào)，2022，54（11）：137-150.

［19］ SHAO D，XU S C，DU A M.Dynamic friction modelling and parameter identification for electromagnetic valve actuator［J］.Journal of Central South University，2018，25（12）：3004-3020.

［20］ 閆樂(lè)樂(lè)，李輝.基于復(fù)合混沌序列的動(dòng)態(tài)密鑰AES加密算法［J］.計(jì)算機(jī)科學(xué)，2017，44（6）：133-138.

［21］ 張?jiān)?Logistic混沌映射［J］.電腦知識(shí)與技術(shù)，2008，35（4）：2538-2539.

［22］ SHI Y，EBERHART R.A modified particle swarm optimizer［C］//1998 IEEE International Conference on Evolutionary Computation Proceedings.Piscataway，NJ：IEEE，1998：69-73.

［23］ 路復(fù)宇，童寧寧，馮為可，等.自適應(yīng)雜交退火粒子群優(yōu)化算法［J］.系統(tǒng)工程與電子技術(shù)2022，44（11）：3470-3476.

［24］ RAMBABU M，BHOOKYA N.GMPPT by using PSO based on Levy flight for photovoltaic system under partial shading conditions［J］.IET Renewable Power Generation，2020，14（7）：1143-1155.

［25］ YAO X，LIU Y，LIN G M.Evolutionary programming made faster［J］.IEEE Transactions on Evolutionary Computation，1999（3）：82-102.

（收稿日期：2023-05-16，修回日期：2023-05-26）

S-type Adaptive Mayfly Algorithm Based on Larval Migration Mechanism

ZHANG Heng-qia，b， QIAN Qiana，b

（a. Faculty of Information Engineering and Automation；? b. Yunnan Key Laboratory of Computer

Technology Applications ， Kunming University of Science and Technology ）

Abstract? ?Considering Mayfly algorithms（MA） poor searching ability， shortcomings in the individual information utilization of excellent offspring and the troubles to fall into local convergence in the middle and late calculation which affects the optimization effect， S-type adaptive mayfly algorithm based on larval migration mechanism （S-AMA） was proposed to solve above problems. Firstly， the S-AMA has Logistic chaotic mapping used to initialize both male and female mayfly populations and increase the diversity of the populations. Secondly， it has the Mayfly life cycle modeled and the S-type life coefficient added to replace the original gravity inertia coefficient to dynamically adjust the balance between the exploration ability and development ability of the algorithm； finally， through considering the life cycle in oxygen-deficient environment of a mayfly， a larval migration mechanism was introduced to strengthen the ability of the superior offspring to get out of local optimum and improve the convergence accuracy of the algorithm so as to enhance the convergence accuracy of the algorithm and search the region near the optimal solution more fully. In the experimental part， S-AMA was applied to the standard function test set， and the optimization contrast experiment and Wilcoxon rank sum test were performed respectively. The results show that the S-AMA algorithm has better optimization ability， convergence speed and robustness than the comparison algorithms. In the experiment， making use of standard function test set to compare the searching ability of the S-AMA with some other algorithms and implement the Wilcoxon rank sum test shows that， as compared to the contrast algorithm， the S-AMA has good optimization ability， convergence speed and strong robustness.

Key words? ?S-AMA， larval migration mechanism， chaotic mapping， S-type life coefficient， Levy flight