中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡

張思雨 韓繼偉 趙倩

摘 ? 要： 培養(yǎng)中學(xué)生數(shù)學(xué)問題解決能力是中學(xué)數(shù)學(xué)課程與教學(xué)的重要目標(biāo)之一。該研究采用認(rèn)知網(wǎng)絡(luò)分析法探索中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡，表現(xiàn)為：首先具備問題轉(zhuǎn)化能力與解題方案執(zhí)行能力，進(jìn)而具備問題轉(zhuǎn)化能力、解題方案執(zhí)行能力與問題結(jié)構(gòu)化能力，最終具備解題方案制訂能力在內(nèi)的數(shù)學(xué)問題解決各維度能力。其中，問題結(jié)構(gòu)化能力是促使中學(xué)生數(shù)學(xué)問題解決能力從低水平到中水平的關(guān)鍵，解題方案制訂能力是促使中學(xué)生數(shù)學(xué)問題解決能力從中水平到高水平的關(guān)鍵。

關(guān)鍵詞： 數(shù)學(xué)問題解決能力；發(fā)展軌跡；認(rèn)知網(wǎng)絡(luò)分析法

一、問題的提出

培養(yǎng)學(xué)生的問題解決能力始終是數(shù)學(xué)教育的一大重心。在我國早期的數(shù)學(xué)課程文本（教學(xué)大綱、課程標(biāo)準(zhǔn)等）中，就顯現(xiàn)出對學(xué)生數(shù)學(xué)問題解決能力的要求，例如，要讓學(xué)生通過學(xué)習(xí)算數(shù)、幾何等知識，掌握基本的謀生技能。1 目前，數(shù)學(xué)問題解決能力的內(nèi)涵進(jìn)一步豐富，指學(xué)生將他們所學(xué)的數(shù)學(xué)知識與技能綜合應(yīng)用于新的問題情境的能力。2 無論是早期以“謀生之計”和“運算”為內(nèi)核的解應(yīng)用題能力，還是現(xiàn)在強調(diào)綜合運用多種知識與技能來解決問題，培養(yǎng)學(xué)生的數(shù)學(xué)問題解決能力一直是基礎(chǔ)教育數(shù)學(xué)課程的目標(biāo)之一。不僅如此，數(shù)學(xué)問題解決能力還是國際學(xué)生評估項目（如PISA）的重要測評內(nèi)容，以及國際數(shù)學(xué)教育大會（ICME）的專項研討課題之一。3 盡管數(shù)學(xué)問題解決能力的研究已取得了很大的進(jìn)展，但多是重視對解題策略的訓(xùn)練與思想方法的滲透，或?qū)W(xué)生水平表現(xiàn)的調(diào)查，缺少對數(shù)學(xué)問題解決能力發(fā)展過程的思考。事實上，若要有效提高學(xué)生的數(shù)學(xué)問題解決能力，不僅需要了解相關(guān)的教學(xué)策略，評估學(xué)生現(xiàn)階段的表現(xiàn)，還有必要理解學(xué)生數(shù)學(xué)問題解決能力是如何隨著學(xué)習(xí)而發(fā)展變化的。隨著教育大數(shù)據(jù)與學(xué)習(xí)分析的快速發(fā)展，認(rèn)知網(wǎng)絡(luò)分析法逐漸應(yīng)用于建構(gòu)復(fù)雜問題領(lǐng)域的思維發(fā)展過程。1 這為本研究提供了重要參考。因此，本研究運用認(rèn)知網(wǎng)絡(luò)分析法，通過可視化表征中學(xué)生數(shù)學(xué)問題解決能力結(jié)構(gòu)，分析其結(jié)構(gòu)特征，探究中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡，以期為數(shù)學(xué)課程、數(shù)學(xué)教學(xué)與評價提供研究基礎(chǔ)和參考依據(jù)。

二、文獻(xiàn)綜述

1.數(shù)學(xué)問題解決能力相關(guān)研究

數(shù)學(xué)問題解決能力是一種高級認(rèn)知能力2，與數(shù)學(xué)核心素養(yǎng)的多個成分密切相關(guān)。關(guān)于數(shù)學(xué)問題解決能力的構(gòu)成要素，邁耶（Mayer）認(rèn)為，數(shù)學(xué)問題解決能力包括轉(zhuǎn)換能力、整合能力、計劃與監(jiān)控能力、實施解決方案能力；3 后來，舍恩菲爾德（Schoenfeld）在前人的理論基礎(chǔ)上，增加和突出了元認(rèn)知和情意因素。4 關(guān)于數(shù)學(xué)問題解決能力的影響因素研究，大多聚焦于數(shù)學(xué)信念、自我效能感等非認(rèn)知因素和教學(xué)因素等，如馬克·普倫德加斯特（Mark Prendergast）等人發(fā)現(xiàn)，學(xué)生積極的數(shù)學(xué)信念是影響其數(shù)學(xué)問題解決能力的重要因素；5 綦春霞等人發(fā)現(xiàn)，初中生的自我效能感對數(shù)學(xué)問題解決能力有正向預(yù)測作用，數(shù)學(xué)焦慮起反向預(yù)測作用；6 鄭太年等人提出，教師在課程教學(xué)的積極態(tài)度以及計算機(jī)輔助教學(xué)對于學(xué)生問題解決能力有正向影響，講授教學(xué)法對學(xué)生問題解決能力有負(fù)向影響。7

綜上可知，已有關(guān)于數(shù)學(xué)問題解決能力的研究，大多是重視對解題策略的訓(xùn)練與思想方法的滲透，或?qū)W(xué)生數(shù)學(xué)問題解決能力水平進(jìn)行評價。然而，若要有效提高學(xué)生的數(shù)學(xué)問題解決能力，不僅需要厘清數(shù)學(xué)問題解決能力的結(jié)構(gòu)及影響因素、調(diào)查學(xué)生數(shù)學(xué)問題解決能力的水平高低，更需要從學(xué)生自身的角度來思考，其數(shù)學(xué)問題解決能力是如何隨著不斷地學(xué)習(xí)而發(fā)展變化的。這不僅是數(shù)學(xué)教育研究發(fā)展的趨勢，也是數(shù)學(xué)教育實踐發(fā)展的訴求。知識或能力之間的聯(lián)系會隨著人們學(xué)習(xí)的進(jìn)步而越來越緊密，最終形成一個更加完善的認(rèn)知框架。8 但目前相關(guān)的實證研究并不豐富，因此，本研究將繼續(xù)分析學(xué)生數(shù)學(xué)問題解決能力中各元素間的內(nèi)在關(guān)聯(lián)和結(jié)構(gòu)，以探究如何發(fā)展學(xué)生數(shù)學(xué)問題解決能力。

2.認(rèn)知網(wǎng)絡(luò)分析法及其應(yīng)用研究

認(rèn)知網(wǎng)絡(luò)分析法（Epistemic Network Analysis，以下簡稱ENA）是由謝弗（Shaffer）等人提出的一種建構(gòu)復(fù)雜問題領(lǐng)域的思維發(fā)展的分析方法。9 其主要優(yōu)勢在于能夠通過網(wǎng)絡(luò)圖，可視化表征被試各能力之間的聯(lián)系及發(fā)展趨勢。具體來說，ENA以“節(jié)點”表示研究框架所包含的元素，再利用二進(jìn)制編碼方式計算這些“節(jié)點”之間關(guān)聯(lián)的強弱，并用網(wǎng)絡(luò)圖的形式呈現(xiàn)元素之間的結(jié)構(gòu)特征，橫向組間或縱向組內(nèi)對比不同的元素結(jié)構(gòu)，從而實現(xiàn)差異化分析或發(fā)展趨勢研究。

ENA方法的優(yōu)勢使其在探究認(rèn)知發(fā)展方面發(fā)揮了重要作用。12 例如，吳忭等人通過ENA方法分析學(xué)生在協(xié)作編程活動過程中，計算思維能力不同維度之間的關(guān)聯(lián)特征，探究了不同能力水平的小組在計算思維能力水平上的差異及其發(fā)展軌跡，指出學(xué)生計算思維結(jié)構(gòu)存在雙向的思維特征；3 冷靜等人通過ENA方法編碼反思日志，揭示了教師反思能力發(fā)展軌跡，即教師逐漸向?qū)υ挿此肌⑴行苑此嫉雀咚侥芰Πl(fā)展過渡；4 喬新虹通過認(rèn)知網(wǎng)絡(luò)分析法來研究教學(xué)設(shè)計能力、添加的教學(xué)設(shè)計能力、辨分的教學(xué)設(shè)計能力和反思的教學(xué)設(shè)計能力之間的關(guān)聯(lián)，及其在實驗前后的變化，驗證了KI課程對職前科學(xué)教師教學(xué)設(shè)計能力發(fā)展的促進(jìn)作用；5 張思等人依據(jù)TPACK框架，應(yīng)用ENA分析了對話反思教師的認(rèn)知網(wǎng)絡(luò)結(jié)構(gòu)特征，發(fā)現(xiàn)教師對話的知識類型主要是學(xué)科教學(xué)法知識和一般教學(xué)法知識。6 綜上，雖然ENA方法在教育研究領(lǐng)域得到了廣泛的應(yīng)用，但少見關(guān)于問題解決方面的應(yīng)用。因此，本研究擬運用認(rèn)知網(wǎng)絡(luò)分析法，構(gòu)建不同水平學(xué)生數(shù)學(xué)問題解決能力的認(rèn)知網(wǎng)絡(luò)圖，可視化表征數(shù)學(xué)問題解決能力各維度間的關(guān)聯(lián)和發(fā)展全貌，以實現(xiàn)對學(xué)生數(shù)學(xué)問題解決能力發(fā)展軌跡的刻畫。

三、研究設(shè)計

1.研究問題

本研究基于邁耶提出的學(xué)生解決數(shù)學(xué)問題的四階段理論，以問題轉(zhuǎn)換能力、問題結(jié)構(gòu)化能力、解題方案制訂能力及解題方案執(zhí)行能力為四維度，表征學(xué)生的數(shù)學(xué)問題解決能力。核心問題是中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡是怎樣的？

2.研究對象

研究對象為吉林省三個地級城市中的10所初中的三年級學(xué)生。研究采取分層抽樣和整群抽樣相結(jié)合的方法，以確保研究對象具有一定的代表性。具體而言，首先根據(jù)管理水平、硬件設(shè)施、生源和師資力量等，將學(xué)校分成從優(yōu)質(zhì)到一般的三個層次水平；然后分別在不同層次水平的學(xué)校中隨機(jī)選取三所作為樣本學(xué)校，將被確定為樣本學(xué)校的全體初中三年級學(xué)生作為研究對象。最終，參與測試的學(xué)生人數(shù)共計421名，回收的有效數(shù)據(jù)樣本共計350份。

3.研究工具

研究編制《中學(xué)生數(shù)學(xué)問題解決能力測評卷》，測量中學(xué)生數(shù)學(xué)問題解決能力。通過對測試卷進(jìn)行預(yù)測、調(diào)整，最終測評題的內(nèi)容效度指數(shù)為0.96，大于0.78，即試題具有較好的效度；測評題在項目反應(yīng)理論下的標(biāo)準(zhǔn)誤差值均接近于0，試題對考生能力水平的估計較穩(wěn)定，即試題具備良好的信度；難度參數(shù)的擬合指標(biāo)MNSQ值均在[0.5，1.5]的可接受范圍內(nèi)，擬合指標(biāo)ZSTD值也在[-2，2]的可接受范圍內(nèi)；試題的區(qū)分度參數(shù)均大于0.3，即試題具有良好的區(qū)分度。

4.研究方法

本研究主要采用調(diào)查法中的測試法探究中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡。數(shù)據(jù)分析方法主要包括描述性統(tǒng)計分析、聚類分析、Rasch模型、認(rèn)知網(wǎng)絡(luò)分析。具體而言，首先采用聚類分析、Rasch模型對回收的350份有效測試卷進(jìn)行數(shù)據(jù)分析，將參試學(xué)生劃分成低、中、高三個水平。其次，采用描述性統(tǒng)計的方法刻畫各個水平學(xué)生數(shù)學(xué)問題解決能力的整體狀況。最后，采用認(rèn)知網(wǎng)絡(luò)分析法來描述中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡。

四、研究結(jié)果

1.中學(xué)生數(shù)學(xué)問題解決能力的整體狀況

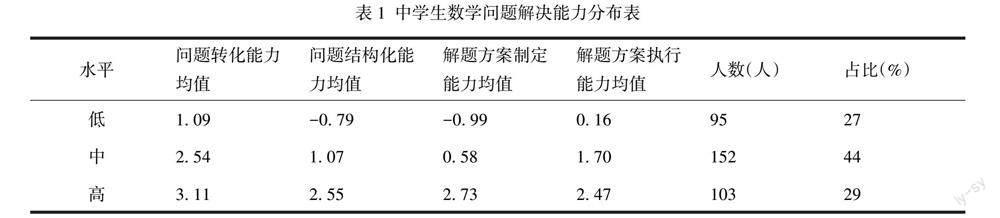
首先，對中學(xué)生數(shù)學(xué)問題解決能力做出如下水平劃分：先根據(jù)Rasch模型計算中學(xué)生數(shù)學(xué)問題解決能力值；進(jìn)而對中學(xué)生數(shù)學(xué)問題解決能力進(jìn)行系統(tǒng)聚類分析，由系譜圖可知，將學(xué)生水平劃分為3類最合適；最后采用K-均值聚類方法，對350名中學(xué)生的數(shù)據(jù)進(jìn)行聚類分析，選擇聚類的集群數(shù)量為3，得到最終的分類結(jié)果。分類結(jié)果表明，低、中與高水平學(xué)生人數(shù)，分別占總?cè)藬?shù)的27%、44%與29%（見表1）。

整體上，中學(xué)生的問題轉(zhuǎn)換能力最強，問題結(jié)構(gòu)化能力與解題方案制訂能力較弱。從低水平到高水平，中學(xué)生數(shù)學(xué)問題解決能力各維度能力均有明顯提升，但不同水平的中學(xué)數(shù)學(xué)問題解決能力結(jié)構(gòu)存在一定的差異，如低水平學(xué)生主要是問題轉(zhuǎn)化能力最強，其次是解題方案執(zhí)行能力；中水平學(xué)生也是如此，但問題結(jié)構(gòu)化能力也有了明顯提升；高水平學(xué)生各維度能力均值均較高。這些描述性分析幫助我們了解中學(xué)生數(shù)學(xué)問題解決能力的整體狀況。然而想要落實對學(xué)生數(shù)學(xué)問題解決能力的培養(yǎng)，我們還需深入理解中學(xué)生的數(shù)學(xué)問題解決能力是如何隨著學(xué)習(xí)而發(fā)展變化的。

2.中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡

首先，以三種水平的中學(xué)生數(shù)學(xué)問題解決能力作為三個分析單元，繪制不同水平的中學(xué)生認(rèn)知網(wǎng)絡(luò)二維質(zhì)心分布圖，以獲得不同水平的中學(xué)生數(shù)學(xué)問題解決能力結(jié)構(gòu)特征，并采用獨立樣本t檢驗比較中學(xué)生數(shù)學(xué)問題解決能力的結(jié)構(gòu)差異；其次，以中學(xué)生的問題轉(zhuǎn)換能力、問題結(jié)構(gòu)化能力、解題方案制訂能力及解題方案執(zhí)行能力為四個節(jié)點，構(gòu)建不同水平的中學(xué)生數(shù)學(xué)問題解決能力認(rèn)知網(wǎng)絡(luò)模型，并計算認(rèn)知網(wǎng)絡(luò)連接系數(shù)值，以了解中學(xué)生數(shù)學(xué)問題解決能力各維度間的關(guān)聯(lián)，獲得中學(xué)生數(shù)學(xué)問題解決能力發(fā)展軌跡。

（1）不同水平的中學(xué)生數(shù)學(xué)問題解決能力結(jié)構(gòu)特征分析

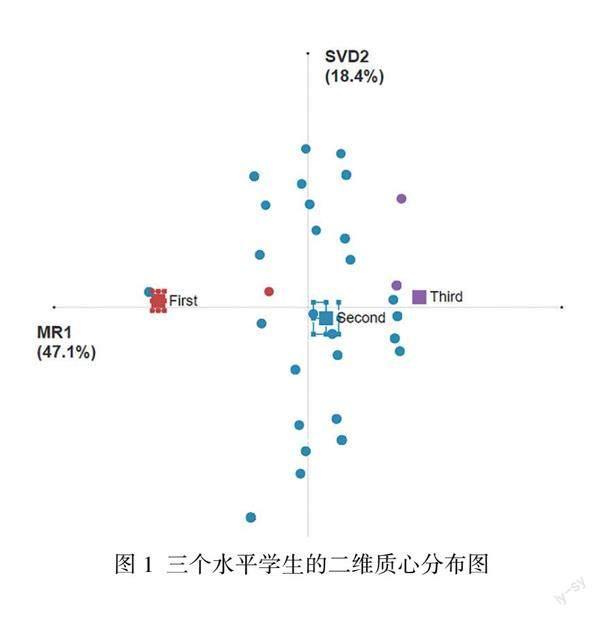
為了探究不同水平的中學(xué)生數(shù)學(xué)問題解決能力結(jié)構(gòu)特征，本研究對中學(xué)生數(shù)學(xué)問題解決能力測評數(shù)據(jù)進(jìn)行預(yù)處理及編碼，建立了三個水平學(xué)生的認(rèn)知網(wǎng)絡(luò)二維質(zhì)心分布圖（如圖1所示）。數(shù)據(jù)結(jié)果顯示，二維質(zhì)心分布圖投影中第一維度（MR1，即X軸）占數(shù)據(jù)總體方差的47.1%，第二維度（SVD2，即Y軸）占數(shù)據(jù)總體方差的18.4%。因此，該模型在統(tǒng)計意義上能夠反映原始數(shù)據(jù)的信息。此外，三個水平學(xué)生的數(shù)學(xué)問題解決能力數(shù)據(jù)投影到二維空間中的三個質(zhì)心位置（圖1中的三個正方形），分別處于不同位置：低水平學(xué)生的質(zhì)心位置距離數(shù)學(xué)問題解決能力各維度均較遠(yuǎn)，中水平學(xué)生的質(zhì)心位置主要靠近問題結(jié)構(gòu)化能力、問題轉(zhuǎn)化能力和解題方案執(zhí)行能力，高水平學(xué)生的質(zhì)心位置距離數(shù)學(xué)問題解決能力各維度能力均較近。這表明，不同水平的中學(xué)生數(shù)學(xué)問題解決能力結(jié)構(gòu)存在較大的差異。

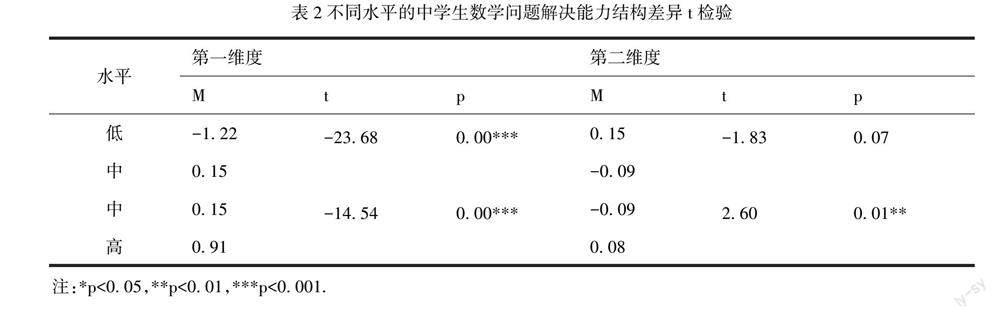
本研究采用獨立樣本t檢驗的方法，對不同水平的中學(xué)生數(shù)學(xué)問題解決能力的平均認(rèn)知網(wǎng)絡(luò)中心位置進(jìn)行差異性檢驗。結(jié)果如表2所示：低水平與中水平的平均認(rèn)知網(wǎng)絡(luò)，在第一維度上存在顯著性差異（p=0.00），而在第二維度上沒有顯著性差異（p=0.07）；中水平與高水平的平均認(rèn)知網(wǎng)絡(luò)，在第一維度上存在顯著性差異（p=0.00）；在第二維度上也存在顯著性差異（p=0.01）。

綜合認(rèn)知網(wǎng)絡(luò)二維質(zhì)心分布圖和獨立樣本t檢驗結(jié)果可知，不同水平的中學(xué)生數(shù)學(xué)問題解決能力結(jié)構(gòu)存在顯著性差異：低水平與中水平的中學(xué)生在問題結(jié)構(gòu)化能力上存在顯著性差異，中水平學(xué)生與高水平學(xué)生在數(shù)學(xué)問題解決能力各維度上存在顯著性差異。

（2）中學(xué)生數(shù)學(xué)問題解決能力的認(rèn)知網(wǎng)絡(luò)模型分析

上述分析表明，不同水平的中學(xué)生數(shù)學(xué)問題解決能力結(jié)構(gòu)存在較大的差異，這也進(jìn)一步說明了中學(xué)生數(shù)學(xué)問題解決能力在從低到高的發(fā)展過程中發(fā)生了明顯的變化。為進(jìn)一步探究中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡，本研究應(yīng)用ENA構(gòu)建不同水平的中學(xué)生數(shù)學(xué)問題解決能力的認(rèn)知網(wǎng)絡(luò)模型，具體包括平均認(rèn)知網(wǎng)絡(luò)圖及認(rèn)知網(wǎng)絡(luò)疊減圖。平均認(rèn)知網(wǎng)絡(luò)圖的結(jié)果顯示：低水平的中學(xué)生主要在問題轉(zhuǎn)化能力、問題結(jié)構(gòu)化能力與解題方案執(zhí)行能力之間有線段連接，但線段非常細(xì)，連接系數(shù)較弱，分別是0.01、0.02、0.04；中水平的學(xué)生數(shù)學(xué)問題解決能力各維度之間均有線段連接，但線段有粗有細(xì)，即連接系數(shù)強弱不一，其中，問題轉(zhuǎn)化能力、問題結(jié)構(gòu)化能力與解題方案執(zhí)行能力之間的連接系數(shù)最強，分別是0.36、0.25、0.24；高水平的中學(xué)生數(shù)學(xué)問題解決能力各維度之間的連接線段較粗，連接系數(shù)均最強，其數(shù)學(xué)問題解決能力的認(rèn)知網(wǎng)絡(luò)結(jié)構(gòu)最穩(wěn)定、平衡。認(rèn)知網(wǎng)絡(luò)疊減圖的結(jié)果顯示：從低水平發(fā)展至中水平的過程中，中學(xué)生的問題結(jié)構(gòu)化能力與其他各維度能力的連接系數(shù)增幅最大，分別是0.32、0.28、0.24；從中水平發(fā)展至高水平的過程中，中學(xué)生的解題方案制訂能力與其他能力連接系數(shù)的增幅最大，分別是0.19、0.17、0.12。

以上數(shù)據(jù)分析結(jié)果表明，學(xué)生處于低水平時，具備一定的問題轉(zhuǎn)化能力與解題方案執(zhí)行能力。即在中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展過程中，中學(xué)生所應(yīng)具備的最基礎(chǔ)能力是問題轉(zhuǎn)化能力與解題方案執(zhí)行能力。學(xué)生處于中水平時，其數(shù)學(xué)問題解決能力結(jié)構(gòu)特征，表現(xiàn)為以問題轉(zhuǎn)化能力、解題方案執(zhí)行能力與問題結(jié)構(gòu)化能力為主。從低水平至中水平的發(fā)展過程中，中學(xué)生的問題結(jié)構(gòu)化能力提升的最為明顯。學(xué)生處于高水平時，其數(shù)學(xué)問題轉(zhuǎn)化能力結(jié)構(gòu)特征，表現(xiàn)為各維度能力之間連接緊密并趨于平衡狀態(tài)。從中水平至高水平的發(fā)展過程中，學(xué)生解題方案制訂能力提升的最為明顯。

五、結(jié)論與建議

本研究基于認(rèn)知網(wǎng)絡(luò)分析方法，得出了符合中學(xué)生認(rèn)知發(fā)展規(guī)律的數(shù)學(xué)問題解決能力發(fā)展軌跡，希望能夠為培養(yǎng)中學(xué)生數(shù)學(xué)問題解決能力，提供一定的理論依據(jù)與實證經(jīng)驗。

1.研究結(jié)論

通過對中學(xué)生數(shù)學(xué)問題解決能力各維度能力均值的描述性統(tǒng)計分析，以及不同水平的中學(xué)生數(shù)學(xué)問題解決能力結(jié)構(gòu)的認(rèn)知網(wǎng)絡(luò)分析，研究發(fā)現(xiàn)，中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡為：問題轉(zhuǎn)化能力與解題方案執(zhí)行能力——問題轉(zhuǎn)化能力、解題方案執(zhí)行能力與問題結(jié)構(gòu)化能力——數(shù)學(xué)問題解決能力各維度能力。其中，結(jié)構(gòu)化能力是促使中學(xué)生數(shù)學(xué)問題解決能力從低水平發(fā)展到中水平的關(guān)鍵，解題方案制訂能力是促使中學(xué)生數(shù)學(xué)問題解決能力從中水平發(fā)展到高水平的關(guān)鍵。

（1）問題轉(zhuǎn)化能力與解題方案執(zhí)行能力是中學(xué)生數(shù)學(xué)問題解決的基礎(chǔ)能力

在中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展過程中，問題轉(zhuǎn)化能力與解題方案執(zhí)行能力首先在低水平階段得以表現(xiàn)。該水平的中學(xué)生能夠用所學(xué)的數(shù)學(xué)知識對現(xiàn)實問題進(jìn)行思考，將外部情境信息轉(zhuǎn)化成數(shù)學(xué)符號語言的內(nèi)在表征，并能使用數(shù)學(xué)符號進(jìn)行推理或運算。這表明，問題轉(zhuǎn)化能力與解題方案執(zhí)行能力是中學(xué)生數(shù)學(xué)問題解決的基礎(chǔ)能力。這是因為，中學(xué)生的問題轉(zhuǎn)化能力在很大程度上與其該領(lǐng)域的知識儲備量相關(guān)。當(dāng)學(xué)生習(xí)得問題領(lǐng)域的知識后，學(xué)生往往能夠根據(jù)自己的基礎(chǔ)知識將問題中的陳述句轉(zhuǎn)換為相應(yīng)的數(shù)學(xué)符號語言。同時，運算能力或使用數(shù)學(xué)符號執(zhí)行推理過程的能力貫穿學(xué)生數(shù)學(xué)學(xué)習(xí)的全過程，因此學(xué)生能具備一定的運算和推理經(jīng)驗。

（2）問題結(jié)構(gòu)化能力是促使中學(xué)生數(shù)學(xué)問題解決能力從低水平發(fā)展至中水平的關(guān)鍵

在中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展過程中，雖然中學(xué)生問題結(jié)構(gòu)化能力在低水平階段也有所體現(xiàn)，但非常薄弱，而在中水平階段的表現(xiàn)最強，且相比其他維度能力，中學(xué)生數(shù)學(xué)問題解決能力從低水平發(fā)展至中水平的過程中，其問題結(jié)構(gòu)化能力的提升幅度最為明顯。這表明，問題結(jié)構(gòu)化能力是促使中學(xué)生數(shù)學(xué)問題解決能力從低水平發(fā)展至中水平的關(guān)鍵。這是因為，學(xué)生的問題結(jié)構(gòu)化能力主要表現(xiàn)為學(xué)生將轉(zhuǎn)譯的各個陳述句整合在一起，形成一個熟悉的問題模型的能力。學(xué)生需要先從轉(zhuǎn)移的信息中選擇與問題相關(guān)的信息，刪除無關(guān)的信息，同時推論題目中沒有的隱藏信息，才能建構(gòu)一個問題模型。1 這往往需要學(xué)生具備較為完善的知識結(jié)構(gòu)以及對數(shù)學(xué)邏輯與數(shù)學(xué)意義的深刻理解。亦即，問題結(jié)構(gòu)化能力是造成熟手與新手解題差異的主要原因之一。較高水平的學(xué)生在解決數(shù)學(xué)問題時通常能夠?qū)栴}背后的知識點有機(jī)地聯(lián)系在一起，整合成熟悉的問題模式，從而能把握問題的實質(zhì)。

（3）解題方案制訂能力是促使中學(xué)生數(shù)學(xué)問題解決能力從中水平發(fā)展至高水平的關(guān)鍵

在中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展過程中，高水平學(xué)生的解題方案制訂能力值遠(yuǎn)大于中水平學(xué)生，且從中水平發(fā)展到高水平的過程中，中學(xué)生解題方案制訂能力的提升幅度最大。這表明，解題方案制訂能力是促使中學(xué)生數(shù)學(xué)問題解決能力從中水平發(fā)展至高水平的關(guān)鍵。這是因為，學(xué)生的解題方案制訂能力主要表現(xiàn)為學(xué)生從長時記憶中尋找與該問題相關(guān)的解決方法，并監(jiān)測自己的解題思路，從而產(chǎn)生對問題的理解與應(yīng)對策略。而在制訂解題方案時，完備的基礎(chǔ)知識是學(xué)生選擇恰當(dāng)?shù)慕鉀Q方案的前提1； 準(zhǔn)確把握問題的實質(zhì)有利于學(xué)生找到合適的解決方法。那么，在培養(yǎng)解題方案制訂能力之前，學(xué)生不僅需要具備基本的問題轉(zhuǎn)化能力，還要具備一定的問題結(jié)構(gòu)化能力。

（4）中學(xué)生數(shù)學(xué)問題解決能力各維度協(xié)同發(fā)展

研究發(fā)現(xiàn)，中學(xué)生數(shù)學(xué)問題解決能力各維度不是孤立產(chǎn)生、發(fā)展的，而是協(xié)同提升、共同強化的。具體來看，當(dāng)學(xué)生問題轉(zhuǎn)化能力與解題方案執(zhí)行能力發(fā)展到學(xué)生能夠基本理解的程度時，問題結(jié)構(gòu)化能力逐漸產(chǎn)生了，進(jìn)而學(xué)生的問題轉(zhuǎn)化能力、解題方案執(zhí)行能力、問題結(jié)構(gòu)化能力開始共同發(fā)展，在達(dá)到簡單應(yīng)用的程度時，其逐漸產(chǎn)生解題方案制訂能力，最終學(xué)生各維度能力協(xié)同發(fā)展。這是因為，在低水平階段，中學(xué)生的知識儲備量較少、知識結(jié)構(gòu)較為松散，對數(shù)學(xué)符號語言意義的理解較淺、對基本數(shù)量關(guān)系的推理與運算的感性經(jīng)驗的積累也較少。2 因此，低水平學(xué)生的問題轉(zhuǎn)化能力和解題方案的執(zhí)行能力較弱，只能達(dá)到基本理解的程度。隨著學(xué)習(xí)的深化和解題經(jīng)驗的積累，中學(xué)生問題轉(zhuǎn)化能力和解題方案的執(zhí)行能力會有所提升，與此同時，學(xué)生深度理解問題的實質(zhì)，能夠準(zhǔn)確地將信息整合成熟悉的模式，其問題結(jié)構(gòu)化能力也得到了發(fā)展，整體上可以達(dá)到基本應(yīng)用的中水平階段。最后隨著學(xué)習(xí)的不斷進(jìn)步，學(xué)生具備更完善的知識基礎(chǔ)和熟練的解題運算技巧，能夠正確理解問題，這樣便更易于找到解決方法，并監(jiān)測自己的解題思路3，從而達(dá)到數(shù)學(xué)問題解決能力各維度能力近乎平衡的高水平階段。

2.教學(xué)建議

中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展具備一定的規(guī)律，教師可根據(jù)學(xué)生的發(fā)展規(guī)律設(shè)計相應(yīng)的教學(xué)活動，以使對中學(xué)生數(shù)學(xué)問題解決能力的培養(yǎng)達(dá)到事半功倍的效果。

（1）起始階段，培養(yǎng)其問題轉(zhuǎn)化與方案執(zhí)行能力

首先，幫助學(xué)生豐富其知識儲備量，這將有利于進(jìn)行問題轉(zhuǎn)化。由于數(shù)學(xué)問題的表征形式也會影響學(xué)生的數(shù)學(xué)問題轉(zhuǎn)化能力，教師在講授數(shù)學(xué)問題時，有必要通過引導(dǎo)學(xué)生用自己的話將問題解釋一遍，特別是對數(shù)學(xué)問題情景的理解，來鍛煉學(xué)生的審題意識與表征能力，或幫助學(xué)生豐富“下游命題系統(tǒng)”，即引導(dǎo)學(xué)生根據(jù)命題A推出命題B、C、D等，從而為問題解決提供更多條件信息，特別是在學(xué)生需要將問題轉(zhuǎn)化成方程式時。除此之外，教師還要注意強化學(xué)生的運算能力、使用數(shù)學(xué)符號執(zhí)行推理過程的能力，即注意幫助學(xué)生理解數(shù)學(xué)符號語言的深層次意義，準(zhǔn)確把握運算規(guī)則。

（2）中間階段，著重培養(yǎng)其問題結(jié)構(gòu)化能力

在中間階段，教師不僅需要培養(yǎng)學(xué)生有效加工和提取數(shù)學(xué)問題中單一元素信息的能力，還要注重培養(yǎng)他們將其整合成具有數(shù)學(xué)意義的結(jié)構(gòu)、相互聯(lián)系著的復(fù)合體的能力。在整合數(shù)學(xué)問題中的信息時，教師可以引導(dǎo)學(xué)生采用問題模型的方式將數(shù)學(xué)問題結(jié)構(gòu)化。這樣可以幫助學(xué)生將所遇問題與已有的知識進(jìn)行聯(lián)結(jié)，建構(gòu)情境，重新整合為自身熟悉的問題模型。這將有利于學(xué)生把握問題的實質(zhì)，從而為找到合適的解決方法奠定基礎(chǔ)。

（3）高階階段，著重培養(yǎng)其解題方案制訂能力

高階階段，教師應(yīng)幫助學(xué)生形成自己的知識結(jié)構(gòu)——解題模塊，引導(dǎo)學(xué)生把某類數(shù)學(xué)問題的知識結(jié)構(gòu)用自己的方式理解、在自己的頭腦中形成一個具有內(nèi)部規(guī)律的整體結(jié)構(gòu)，這些結(jié)構(gòu)往往可以用一些圖表等形式進(jìn)行表示。這就可以為學(xué)生制訂解題方案提供多條思路。由于解題模塊的建立還需要考慮問題背后的本質(zhì)與思想，這便需要數(shù)學(xué)教師具有較強的歸納類型和模塊的意識，引導(dǎo)學(xué)生從雜亂無章的問題中概括一般原理，使學(xué)生能夠遷移、應(yīng)用已有的知識和經(jīng)驗。這在某種程度上也解決了“學(xué)生從教師那里學(xué)會例題之后，自己課下不會解題”的教學(xué)問題。此外，我們建議數(shù)學(xué)教師在引導(dǎo)時，還要給學(xué)生的反思和歸納總結(jié)留有足夠的時間，讓學(xué)生主動產(chǎn)生理解與應(yīng)對策略。

六、結(jié)語

如何有效地提高學(xué)生的數(shù)學(xué)問題解決能力一直是數(shù)學(xué)教育研究的重要議題。本研究應(yīng)用認(rèn)知網(wǎng)絡(luò)分析法，可視化表征了中學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡。這是從學(xué)生自身發(fā)展的角度來思考這一問題的，符合學(xué)生認(rèn)知發(fā)展規(guī)律。由于本研究主要基于邁耶提出的學(xué)生解決數(shù)學(xué)問題的四階段理論，從問題轉(zhuǎn)換能力、問題結(jié)構(gòu)化能力、解題方案制訂能力及解題方案執(zhí)行能力四個維度表征學(xué)生的數(shù)學(xué)問題解決能力，發(fā)展變量僅有四個，因而在發(fā)展軌跡的精細(xì)度上具有一定局限性。未來研究將進(jìn)一步優(yōu)化、細(xì)分學(xué)生數(shù)學(xué)問題解決能力的維度表征，更精準(zhǔn)地刻畫學(xué)生數(shù)學(xué)問題解決能力的發(fā)展軌跡，為數(shù)學(xué)課程、數(shù)學(xué)教學(xué)與評價提供更精細(xì)的研究基礎(chǔ)和參考依據(jù)。

The Developmental Trajectory of Middle School Students Mathematical

Problem Solving Ability：A Study Based on Epistemic Network Analysis

ZHANG Siyu，HAN Jiwei，ZHAO Qian

（School of Mathematics and Statistics，Northeast Normal University，Changchun，Jilin，130024）

Abstract： Cultivating studentsmathematical problem solving ability is one of the important goals of mathematics curriculum and teaching in middle schools. This study adopts epistemic network analysis to explore the development trajectory of middle school students mathematical problem solving ability，which include the followings： firstly，students should acquire the competencies of problem transformation and problem solving scheme execution；then they will acquire the competency of problem structuring in addition to the first two competencies；and finally they will acquire the competency of mathematical problem solving ability in all dimensions，including the competendcy of problem solving scheme formulation. Among them， the competency of problem structuring is the key to promoting the development of students mathematical problem solving ability from low level to medium level，and the competency of problem solving scheme formulation is the key to promoting the development of their mathematical problem solving ability from medium level to high level.

Key words： mathematical problem solving ability，development trajectory，epistemic network analysis