基于比例風險模型的飛機部件剩余壽命預測

何 浪，魯 亮+，陸錦鶴，范圣嫻，趙立新，張宇翔

(1.中國民航大學 計算機科學與技術學院，天津 300300；(2.北京飛機維修工程有限公司 附件/起落架大修產品事業部，北京 100621)

0 引 言

全球的空中交通運輸量正在快速增加，預計到2037年民航客機總數將達到45 265架[1]。在商業運營中，民用飛機的維修成本通常占航空公司直接運營成本的10%～20%[2]，準確預測飛機部件從當前狀態到失效狀態的剩余壽命可以提早預警飛機部件故障，并合理制定維修計劃，從而有效降低維修成本，這在航空公司的安全運行和成本控制方面至關重要。

在現有工業設備的剩余壽命預測方法中[3，4]，基于數據驅動的方法不依賴設備的失效原理，而是通過對設備運行數據進行建模分析來預測設備剩余壽命，因而被廣泛使用。該方法可大致分為基于退化數據的方法和基于失效數據的方法兩類[5]。前者雖然可以通過多傳感器信息提高剩余壽命預測的精度[6-8]，但是增加了系統的復雜性及成本[9]；而后者則需選擇合適的壽命分布，且需要足夠的失效數據進行分布擬合。文獻[10，11]分別解決了壽命分布的選擇問題和分布擬合的數據量問題，但沒有考慮飛機各部件壽命的個體差異。事實上，一些飛機部件在進行拆換時會從備件倉庫中選出調試好的部件進行更換，這些部件可能經歷了不同的飛行時長、維修模式以及維修次數等。此外，文獻[12]中指出，飛機年齡、飛機發動機型號等飛機參數也可能成為影響飛機故障概率的潛在因素。若將這些因素與部件的失效數據結合，可進一步提高壽命預測結果的精確度，并使其具有良好的可解釋性。

比例風險模型(proportional hazard model，PHM)[13]作為一種可以分析多個變量與生存時間之間關系的統計回歸模型，能處理可靠性數據且不需要提前對生存分布進行假設，正逐漸被應用于可靠性領域[14，15]與航空發動機的剩余壽命預測研究中。文獻[16-18]基于該模型分析了多個參數對飛機發動機、輔助動力裝置(auxiliary power unit，APU)等部件壽命的影響，但仍利用部件的狀態監測數據進行壽命預測，忽略了部件狀態以及部件所處環境對其壽命的影響。此外，飛機由大量的子系統和部件組成，很難直接獲取到部分部件可用的狀態監測數據。

本文彌補了基于失效數據方法在考慮部件個體差異時存在的不足，同時規避了基于狀態監測數據的方法存在的問題，綜合運用飛機部件的歷史維修數據和歷史失效數據，提出了一種基于比例風險模型的飛機部件剩余壽命預測方法，并通過對比實驗驗證其有效性。

1 飛機部件剩余壽命預測

1.1 可靠性分析

可靠性分析是剩余壽命預測的基礎[19]。可靠性是指部件在規定條件和規定時間間隔內執行指定功能的能力，涉及失效概率F、可靠度R和失效率h等統計指標。

設壽命T為部件從完好狀態到失效狀態所經歷的時間，失效(故障)概率F表示部件工作時間T小于t時失效的概率，可表示為

(1)

其中，f(x) 表示T的概率密度函數。在工程實踐中，該變量通常通過實驗評估確定。

可靠度R指設備工作時間T大于t的概率，可用式(2)表示

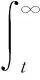
(2)

失效率h描述為設備工作時間到t，并在時刻t后單位時間內失效的概率

(3)

由式(2)可知f(x)=-dR(t)/dt， 代入式(3)中，則有

(4)

對等式(4)左右兩邊同時積分可推出可靠度R與失效率h之間的關系

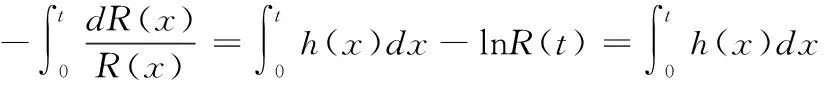
(5)

1.2 比例風險模型

比例風險模型的基本形式定義為

h(t|X)=h0(t)exp(βX)

(6)

其中，h0(t) 表示各特征變量均為0時的基本失效率函數，h(t|X) 表示各特征變量的值均固定時的失效率函數，X=(X1，X2，…，Xp)T為影響部件剩余壽命的特征向量，β=(β1，β2，…，βp) 為相關特征對應的系數向量，表示特征變量對部件壽命的影響程度，p表示特征的個數。

1.2.1 特征選擇

為了保留每個特征的實際意義并避免由自變量之間存在的相關關系，即多重共線性造成的特征冗余，采用逐步回歸法對主要特征進行篩選。逐步回歸法根據檢驗的顯著性對特征變量逐個分析，通過與設定的顯著性水平對比，以此來決定對該特征變量進行引入或者剔除。其步驟如下：

(1)對于未引入的特征變量，從中選擇與因變量相關程度最高的特征變量并建立回歸方程，進行顯著性檢驗。若通過檢驗，則重復該步驟；否則轉步驟(2)。

(2)對于已引入的特征變量，進行顯著性檢驗，若檢驗不通過，則剔除該特征變量，確保每次引入新的特征變量之前回歸方程只包含顯著的變量，轉步驟(1)；否則結束。

此外，在引入特征變量的過程中，其先后順序并不代表其在最終回歸方程中的重要程度，后引入的相對重要的特征變量則會因為多重共線性而被剔除。因此，需要在進行逐步回歸前進行多重共線性的診斷。

多重共線性的診斷方法主要分為兩類，一類是經驗式的診斷方法，包括觀察特征變量的相關系數矩陣、通過專業知識或一般經驗分析回歸系數的代數符號以及某一個特征變量是另一部特征變量的近似線性組合等。另一類為統計診斷方法，其最主要的方法為使用方差膨脹因子。特征變量Xp的方差膨脹因子記為VIFp，公式如下

(7)

1.2.2 比例風險模型假定的檢驗

比例風險模型要求各特征變量的作用效應不隨時間的變化而變化，故在建立比例風險模型前需要進行比例風險假設驗證。現有比例風險假設方法可分為圖示法和假設檢驗法，其中圖示法具有清晰、實用等特點，主要包括Cox &K-M比較法[13]、累積風險函數圖示法[20]以及Schoenfeld殘差法[21]。

Cox &K-M比較法最早由Cox提出，通過將比例風險模型和Kaplan-Meier估計的各組生存曲線進行比較，若曲線的趨勢一致且無交叉，則滿足比例風險假定。

累積風險函數圖示法可通過觀察對數累積風險函數對時間的趨勢圖，若各組曲線互相平行，則滿足比例風險假定。

根據式(6)以及累積風險函數可知

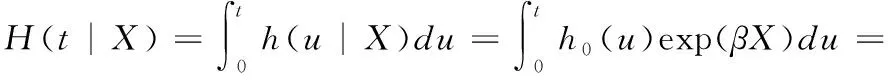
(8)

對等式(8)兩邊取對數

lnH(t|X)=lnH0(t)+βX

(9)

由上式可知，若不同組間的對數累積風險函數差值lnH(t|X1)-lnH(t|X2)=β(X1-X2) 為常數，則對應圖像中各組曲線應保持平行或重疊。

Schoenfeld殘差法最早由Schoenfeld提出，在ti時刻部件的偏殘差ri定義如下

ri=(ri1，ri2，…，rik)

(10)

(11)

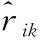
1.2.3 參數估計

由式(6)可知，比例風險模型可以看作基本失效率函數的非參數部分和一個與失效因素線性相關的參數部分的乘積。

對于非參數部分，不同部件的生存時間對應的分布不同。常見的壽命分布函數有正態分布、指數分布、威布爾分布、對數正態分布、伽馬分布等，需選擇最適合部件的分布函數對其生存時間分布進行擬合。首先通過極大似然估計得到相應分布的參數，然后根據AD檢驗統計量的大小選擇合適的分布類型。

對于參數部分，協變量的參數估計通常可以用以下偏似然方程進行求解

(12)

其中，n表示觀測樣本的數量，δi為狀態變量。當δi=0時表示部件在故障前被拆除，δi=1時則表示部件故障時被拆除。

式(12)的對數方程為

(13)

lnL(β) 的一階導數為

(14)

根據式(13)和式(14)，可采用梯度下降法對參數進行估計。另一種辦法則是繼續求出式(13)的二階偏導，然后利用Newton-Raphson方法進行參數估計。該方法雖然收斂快，但是需要計算二階偏導以及矩陣的逆，計算復雜度偏大。

1.3 剩余壽命預測

在獲得參數β的估計值后，將式(6)代入式(5)中可以推出在X條件下的可靠度函數

(15)

對等式(15)兩邊取對數

(16)

剩余壽命的平均值為

(17)

根據式(16)、式(17)可得到t時刻在X條件下的平均剩余壽命

(18)

本文采取固定時間點預測的方式預測部件的剩余壽命。如圖1所示，根據部件的平均更換間隔時間設置預測點t1，t2，…，tn， 在各預測點對飛機輪胎進行剩余壽命的預測。

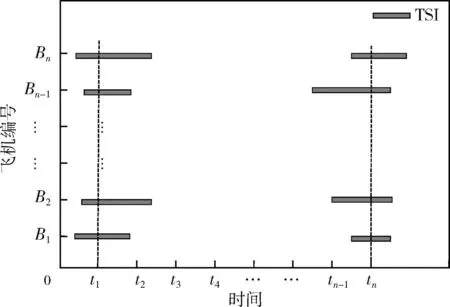
圖1 預測間隔

2 數據集描述

本文使用的數據集收集自北京飛機維修工程有限公司。數據集包含858個部件，共85 259條維修記錄，涉及163架B737 NG型號的飛機，其時間跨度為2016-2019年。數據屬性包括收貨日期、部件編號、維修模式代碼、維修費用、裝機日期、拆卸日期、部件自出廠到現在的累計飛行小時數(time since new，TSN)、部件自上次大修以來的累計飛行小時數(time since overhaul，TSO)、部件本次裝機到拆卸之間的累計飛行小時數(time since install，TSI)，部件本次裝機到拆卸之間的累計飛行小時數、飛機編號、發動機型號、飛機制造日期等。其中，TSI為因變量，表示部件的壽命。根據數據的可用性以及部件的經濟效益，在本文實驗中選擇主輪的裝拆記錄進行數據分析，并從部件自身以及部件所處環境兩個方面進行特征提取。對于主輪自身，TSN、TSO、部件累計維修次數(TIMES)以及維修的模式(MODE)都可能會影響部件的壽命。飛機在減速剎車時，主輪要面臨急劇的溫度變化，可能對輪胎的壽命造成影響，因此可以考慮環境溫度變化的影響，故將季度(Quarter)作為主輪的備選特征。此外，考慮飛機的結構的老化以及發動機推力的不同，也有可能影響主輪的壽命，故將主輪所在飛機的年齡(AGE)和發動機型號(Engine)作為備選特征。表1給出了主輪備選特征描述。

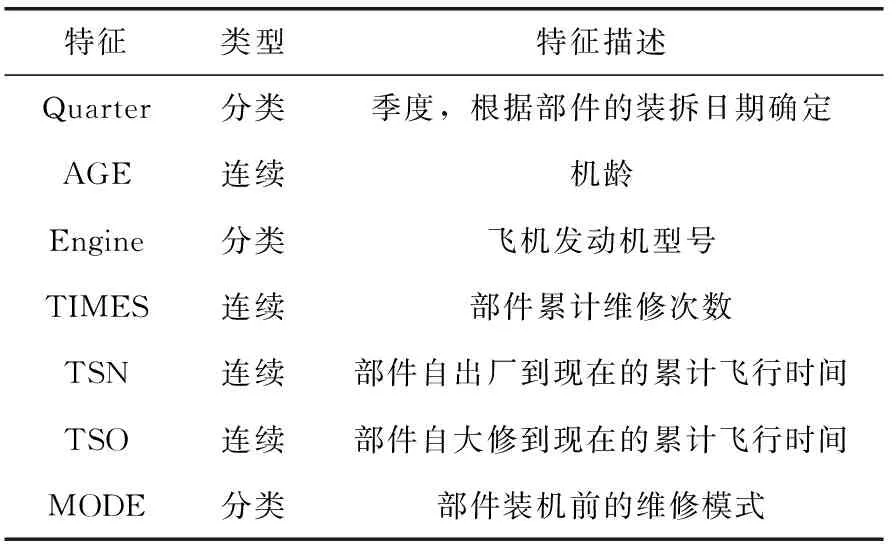
表1 特征描述

表2中為各連續型變量的描述性統計。為了更好地評估這些參數對TSI的影響，需要對這些連續變量進行歸一化。歸一化方法如下

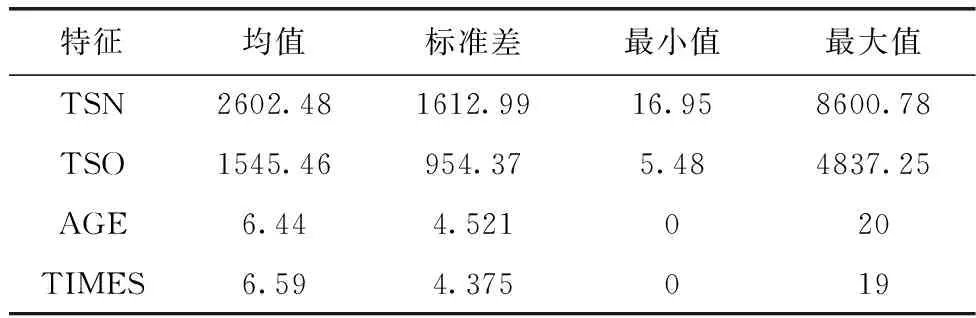
表2 連續變量的描述性統計

(19)

其中，Z1max、Z1min、Z2max、Z2min、Z3max、Z3min、Z4max和Z4min分別表示TSN、TSO、AGE以及TIMES的最大最小值。

對于分類變量，采用箱形圖展示各分類變量關于TSI的數據分布，如圖2所示。

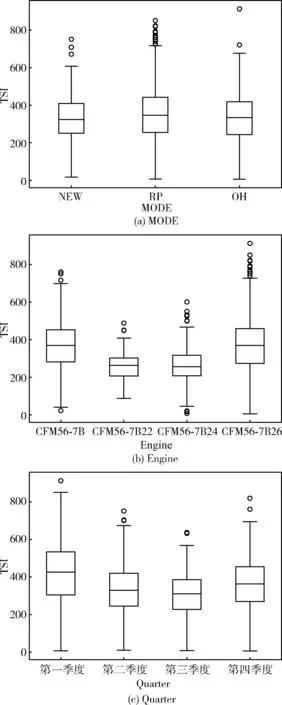
圖2 分類變量的數據分布

在圖2(a)中，維修模式包括新件(NEW)、修理(repair，RP)和大修(overhaul，OH)。

3 模型驗證與分析

3.1 主輪與TSI分布分析

通過常見壽命分布函數對主輪的TSI進行擬合，然后根據AD檢驗統計量選用AD值較小的分布函數。表3中給出了擬合效果較好的分布的參數估計結果。

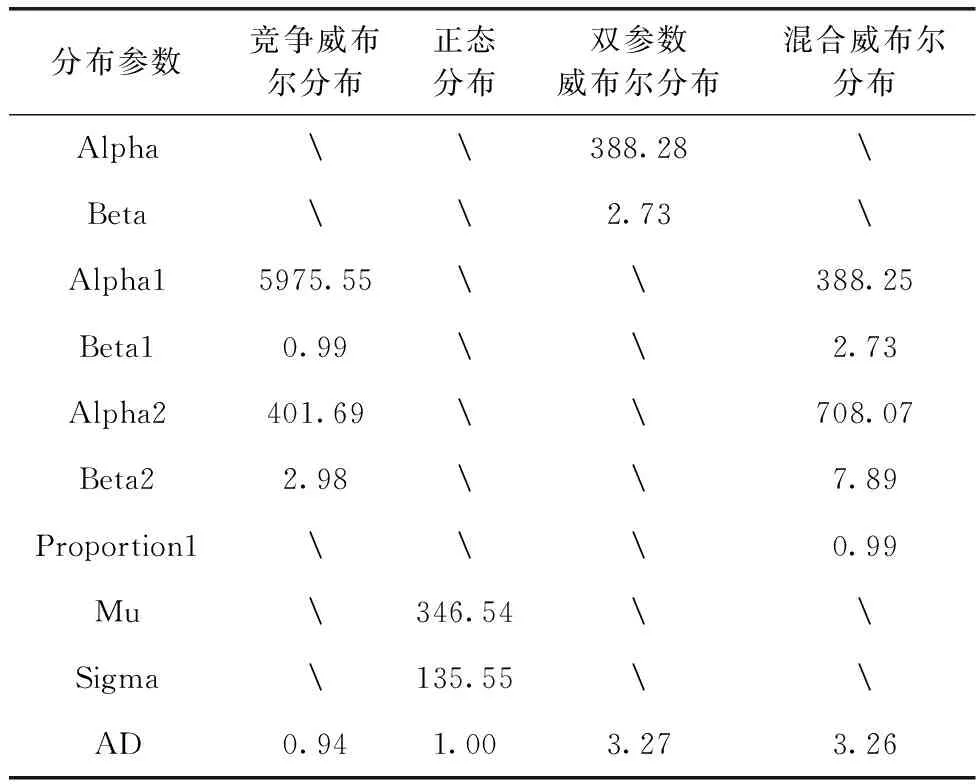
表3 各分布參數估計結果

圖3為各分布的擬合結果，圖中的直方圖為主輪TSI的數據分布。從圖中可以看出這幾種分布曲線與主輪的數據分布都較為接近，擬合的效果較好。

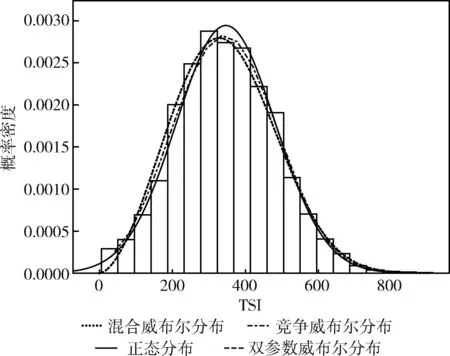
圖3 分布曲線擬合

3.2 檢驗與回歸結果

在逐步回歸篩選的過程中，TIMES與MODE被剔除。其中，TIMES與TSN存在多重共線性，而MODE的顯著性檢驗未通過。通過逐步回歸篩選后，TSN、TSO、AGE、Engine和Quarter是篩選出的對TSI影響最顯著的特征變量。

對主輪進行比例風險回歸建模之前，需要對所選特征變量進行比例風險假設驗證。選擇基于累積風險函數圖示法和Schoenfeld殘差法分別對分類變量和連續變量進行比例風險假設驗證。由圖4可以看出發動機型號、季度等分類變量的對數累積風險函數關于TSI的曲線都基本平行或等距，說明這幾個參數滿足比例風險假定。

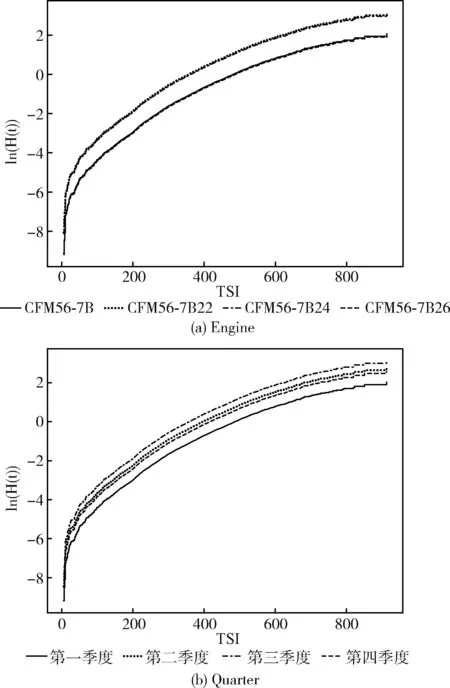
圖4 分類變量的對數累積風險函數

圖5為各連續變量的Schoenfeld殘差圖，可以看出圖中的擬合曲線基本以0為中心波動，滿足比例風險假定。

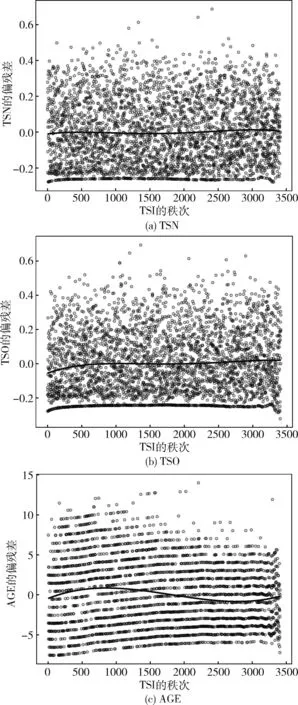
圖5 連續變量的殘差

表4中，維修模式、發動機和季度類型用虛擬變量表示。虛擬變量是指取值為0或1的變量，用于表示分類變量中某些屬性狀態是否存在。根據虛擬變量的設置規則，需要選取一種屬性作為分析的基礎，其它屬性則作為虛擬變量進行分析。以“發動機型號”為例，CFM56-7B、CFM56-7B22、CFM56-7B24和CFM56-7B26這4種型號分別用Engine_1、Engine_2、Engine_3、Engine_4表示，將Engine_1作為參照變量，則Engine_2、Engine_3、Engine_4作為虛擬變量。各變量的系數為β中對應的值，P值表示該變量在設定的顯著性水平(α=0.05)下是否顯著，即該變量對基本失效率h0(t) 的影響是否顯著。HR表示風險比，表示在其它變量保持一定時，該變量對基本失效率的影響程度。

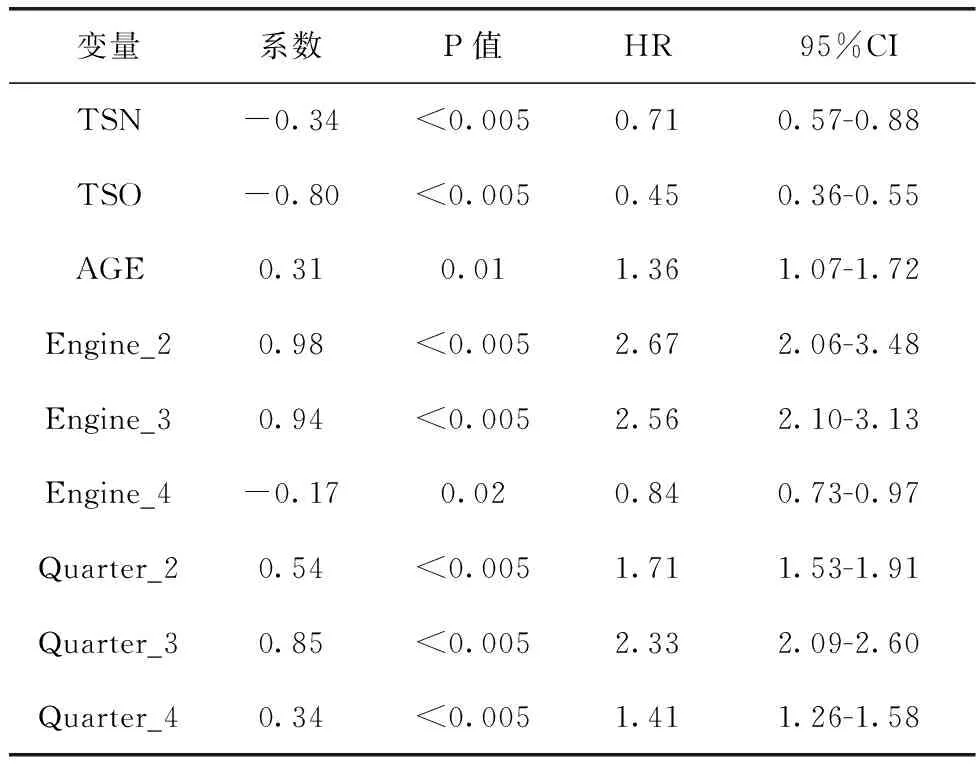
表4 比例風險回歸結果

從表4中可以看出飛機機齡會使輪胎的故障風險增加；裝有CFM56-7B22和CFM56-7B24的飛機上的輪胎更容易故障；第二季度和第三季度輪胎故障的風險更大。飛機輪胎值得注意的是TSN和TSO的HR值意味著當它們增加時輪胎的故障風險會降低，其主要的原因可能是由數據篩選的結果造成的。為了完整跟蹤飛機輪胎從新件到經過數次維修后的連續狀態，本文在數據篩選時選擇了2016-2019期間使用的新輪胎的維修記錄，因此數據中輪胎的累計飛行小時數不足。其次，航空公司現有的維修策略會要求一些部件在經過幾次修理后就會經歷一次大修，使得部件維修記錄中的TSO值也不會太大。

3.3 剩余壽命預測結果分析

3.3.1 比例風險模型預測結果

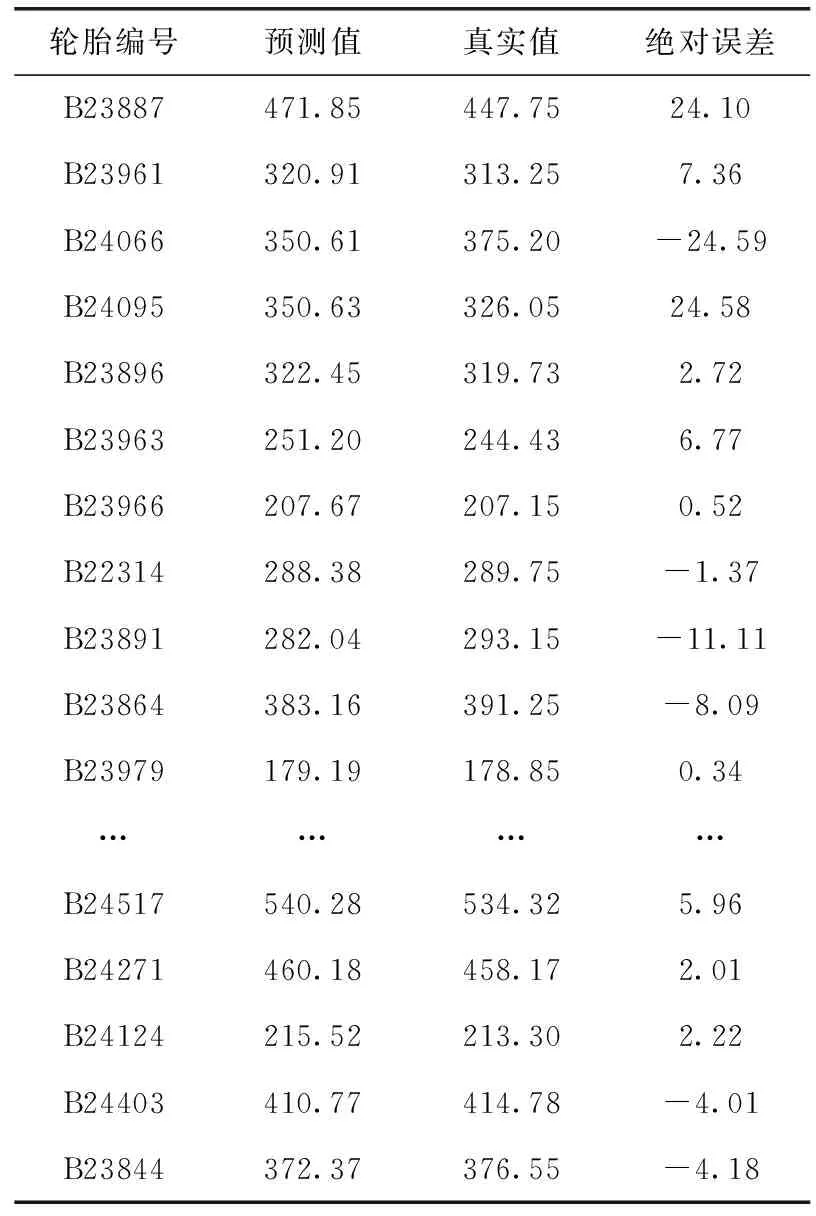
表5 比例風險模型預測結果

3.3.2 對比方法預測結果

為了更好地評估比例風險模型在預測部件剩余壽命時的效果，采用了其它回歸模型進行對比，即將比例風險模型中的特征作為其它回歸模型的參數。由于比例風險模型假設特征變量以乘積的形式影響基本失效率，包含了部件的壽命分布，因此本文在與其它傳統回歸方法對比時，考慮將部件的壽命信息加入到回歸模型中。在文獻[22]中，Kadhem等用威布爾分布對歷史風速數據進行擬合，并用威布爾分布進行隨機采樣生成一個風速數據，通過將該數據與其它影響風速的特征作為人工神經網絡的輸入特征對風速進行預測。此外，在文獻[23]中，He等提出了一種加性平均剩余壽命模型，分析了潛在風險因素對平均剩余壽命的影響。結合上述文獻的數據處理思想，本文對分類回歸樹、多層感知機回歸、多元線性回歸、支持向量回歸以及隨機森林回歸等其它回歸模型分別嘗試了如下兩種不同的改進方法。

根據式(17)，在t1，t2，…，tn時刻計算出對應的平均剩余壽命m(ti)， 其中i=1，2，…，n。

(1)將m(ti) 加入到特征向量X中，作為第p+1個特征。然后將新的特征向量作為其它回歸模型的輸入。

(2)計算m(ti) 與實際剩余壽命的差值并作為因變量，然后將特征向量X作為其它回歸模型的輸入。

按照上述改進方法，使用訓練集對各模型進行訓練，測試集來驗證各模型的預測能力。本文將均方根誤差(RMSE)、平均絕對誤差(MAE)、平均絕對百分誤差(MAPE)作為評估本文方法以及其它方法的指標。這些指標是預測任務中常用的評價指標，數學表達式如下

(20)

(21)

(22)

表6給出了比例風險模型與其它回歸模型壽命預測的結果。其中L表示未改進的回歸模型，L1表示第一種改進，即將m(ti) 加入到特征向量X中，將新的特征向量作為其它回歸模型的輸入。L2表示第二種改進，即計算m(ti) 與實際剩余壽命的差值作為因變量，將特征向量X作為輸入。

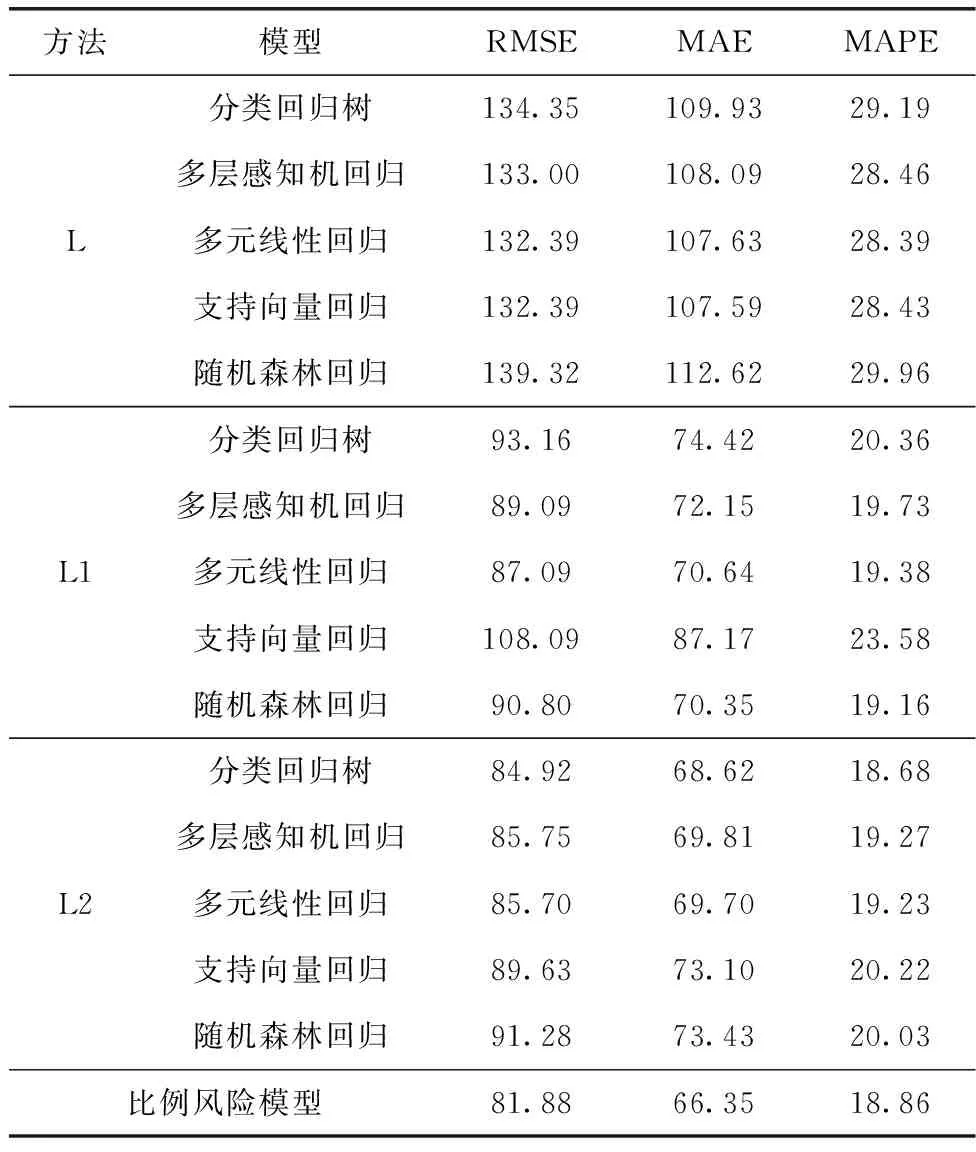
表6 各方法對比結果

可以看出改進后的回歸模型預測精度有了明顯提升。L1和L2相較L的RMSE分別降低了40.63以及46.83，MAE則分別降低了34.23以及38.24。從MAPE來看，L1和L2方法相較L在預測精度上分別平均提升了8.44%以及9.4%。而比例風險模型在3個指標上都要優于其它回歸模型，在整體預測效果上，比例風險模型>L2>L1>L。

4 結束語

本文通過對飛機部件的維修數據進行分析，提出了基于比例風險模型的飛機部件剩余壽命預測方法。通過對飛機主輪進行實例驗證，分析了影響飛機主輪壽命的主要因素以及影響程度，可為部件維修策略的調整提供參考。此外，通過對其它回歸模型進行改進，提供了比例風險模型的對比方法。實驗結果表明，改進后的回歸模型的預測精度平均提升了8.92%，同時比例風險模型的整體預測效果要優于改進后的回歸模型。