基于改進四參數法的法蘭螺栓連接預緊力優化

張陽，趙晶

（沈陽工業大學 機械工程學院，沈陽 110870）

0 引言

由于螺栓預緊彈性的相互作用，會導致已預緊螺栓的預緊力會發生改變，這大大降低了法蘭螺栓連接的可靠性和使用性能。因此，針對由螺栓彈性相互作用的研究已成為螺栓法蘭連接高性能裝配的熱點。

Van Campen等[1]于1969年提出了彈性相互作用系數法，Bibel等[2-3]擴展了該方法。Zhu等[4]使用有限元和實驗方法研究了彈性相互作用的影響。基于彈性相互作用系數法，確定螺栓的初始預緊力，最終得到均勻的目標預緊力。馬躍等[5]的研究表明多輪次預緊能夠有效降低殘余預緊力的分散程度，并將該方法應用到某型盤式發動機螺栓組預緊，得到了令人滿意的結果。Nassar等[6]建立了有限元模型，研究了預緊順序、墊片加載和卸載歷史及預緊力水平對彈性相互作用的影響，通過實驗驗證了有限元方法的有效性；使用逆序列法確定螺栓的初始預緊力，最終得到滿意的結果。Coria等[7-8]基于彈性相互作用系數法開發了四參數法，在保證結果準確性的條件下大大縮減了使用成本；同時，驗證了四參數法在多輪次預緊時的有效性。

以往的文獻中對無墊片法蘭螺栓連接的彈性相互作用的研究還較少，但對很多工業設備來說，采用的往往是無墊片法蘭螺栓連接，尤其是透平壓縮機分體式機殼這種多螺栓密排連接的壓力容器[9]，其均勻的預緊力是保證密封性能的前提。因此，應用有限元分析方法，分析研究無墊片法蘭螺栓預緊力分布情況，根據現有方法中四參數法使用成本低的特點，采用該方法解決預緊力分布不均問題，探討其適用性，最后將四參數法予以改進，進一步提升其結果準確性，為解決透平壓縮機分體式機殼螺栓預緊力分布不均問題提供參考。

1 四參數法

1.1 原理簡介

該方法是基于彈性相互作用系數法改造而來，目的是通過一輪或兩輪預緊，使全部螺栓獲得均勻的目標載荷。建立螺栓初始載荷和最終載荷的矩陣方程：

式中：Sf為全部螺栓預緊后的螺栓最終載荷矩陣；Si為螺栓的初始載荷矩陣。矩陣Sf和Si中的元素一一對應，即矩陣Si的元素Sik是螺栓k的初始載荷，Sf的元素Sfk是螺栓k的最終載荷。

那么在計算出矩陣A后，應用螺栓最終荷載Sf以反求螺栓的初始載荷Si，使用下式計算：

1.2 矩陣A參數計算方法

表1給出了四參數法矩陣A中參數的計算方法，該方法僅考慮螺栓兩側與其相近的4個螺栓的影響，無需模擬螺栓組預緊過程，只需模擬表中的3種情況，并據此計算出4個參數α、β、δ和γ，將這4個參數根據實際的預緊順序填入矩陣A中即可。

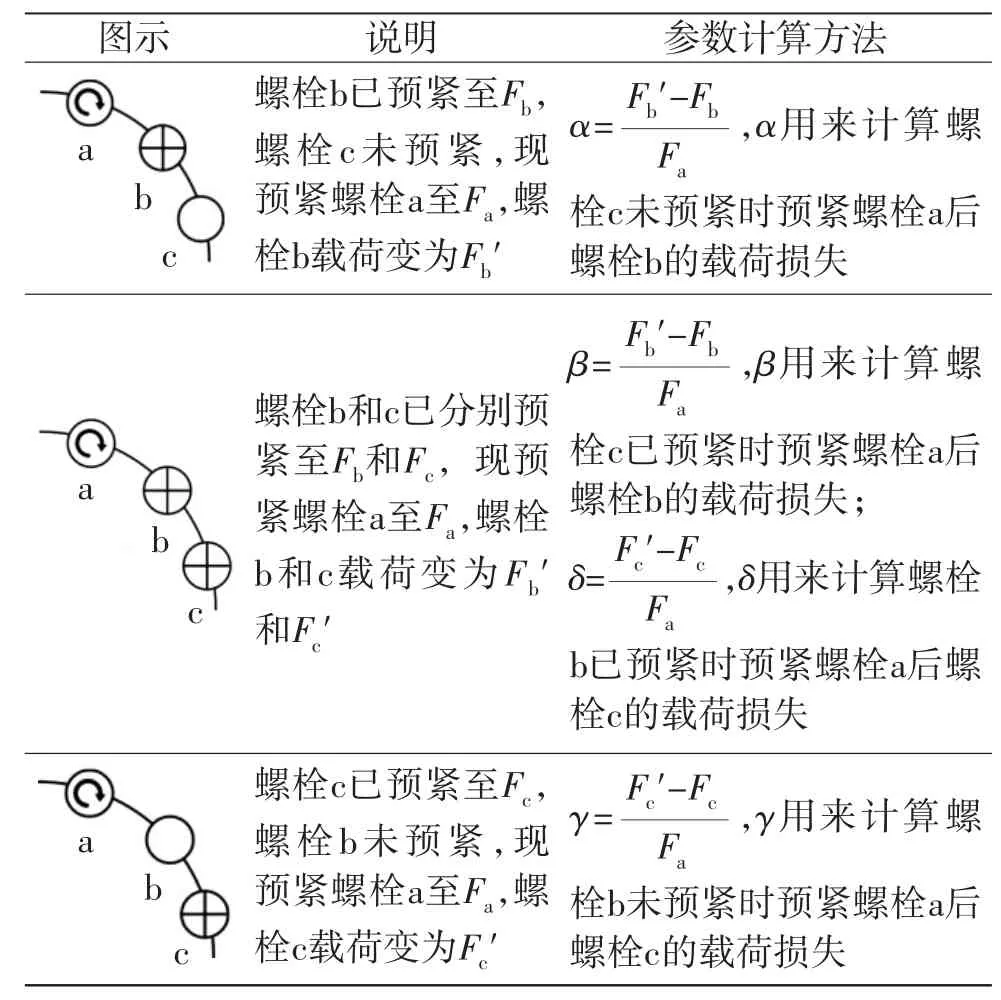
表1 參數計算方法

2 預緊力優化

2.1 有限元模型的建立

建立圖2所示的法蘭螺栓連接有限元模型，法蘭材料為鋼，彈性模量為2×105MPa，泊松比為0.3；螺栓材料為35CrMoA，彈性模量為2.03×105MPa，泊松比為0.3。法蘭與螺栓間及上、下法蘭間的接觸都采用摩擦接觸，其摩擦因數為0.2。對下法蘭的下端面施加固定約束。

圖1 有限元模型

圖2 螺栓編號

何聯格等[10]的研究表明，采用交叉預緊能夠使螺栓的殘余預緊力更加均勻。為了研究無墊片多螺栓法蘭連接預緊力分布規律和四參數法的準確性及特點，螺栓預緊過程采用兩種交叉預緊順序（如圖2）：順序①：1-7-4-10-2-8-5-11-3-9-6-12；順序②：1-7-2-8-3-9-4-10-5-11-6-12。

2.2 結果分析

表2給出了使用四參數法計算的參數α、β、δ和γ。

表2 參數值

表3為根據順序①列出的矩陣A，行代表預緊順序，列代表該螺栓對已預緊螺栓的影響。以第一行為例，該行代表螺栓1預緊后，后預緊螺栓對其影響；當僅預緊螺栓1時，螺栓1未受其他螺栓影響，所以1號螺栓處為1；預緊螺栓2時，螺栓1僅受螺栓2影響，所以螺栓2處為α；預緊螺栓11時，螺栓12未預緊，所以螺栓11處為γ；預緊螺栓3時，螺栓1、2已預緊，所以螺栓3處為δ；預緊螺栓12時，螺栓1、2已預緊，所以螺栓12處為β；其余位置均為0。

表3 矩陣A

因此可以說，任意法蘭螺栓連接都可以計算得到一個矩陣A，不同預緊順序的參數在矩陣A中占據不同的位置。

以50 000 N為目標預緊力，計算兩種預緊順序下螺栓預緊力優化前和經四參數法優化后的預緊力分布情況。計算結果如圖4所示，給出了螺栓組按順序①和順序②兩種不同預緊順序預緊下的各螺栓預緊力分布情況。

從圖3可以看出，優化前在兩種順序下，由于彈性相互作用的存在，殘余預緊力分散程度比較大，即殘余預緊力分布不均勻。值得注意的是，一些螺栓的殘余預緊力處于相似水平，順序①下，12顆螺栓每4顆為一組，1號、4號、7號和10號螺栓預緊力損失最大，2號、5號、8號和11號螺栓次之，3號、6號、9號和12號螺栓預緊力損失最小；順序②下，1號和7號螺栓預緊力損失最大，6號和12號螺栓預緊力損失最小，其余螺栓處于居中的相似水平。這意味著在無墊片法蘭螺栓連接中，預緊力的損失多是由相鄰螺栓引起的，彈性相互作用的影響會隨著螺栓距離的增大而減小，也表明四參數法會有很好的適用性。

圖3 預緊力仿真結果

經四參數法預緊力優化后，兩種順序下，各螺栓殘余預緊力變得較為集中，分散性明顯減小。但是，順序①下，預緊力損失最大的1號、4號、7號和10號螺栓在經四參數法預緊力優化后，殘余預緊力超過了目標預緊力；順序②下，在優化前預緊力損失最大的1號和7號螺栓，經四參數法預緊力優化后殘余預緊力也超過了目標預緊力，這表明該方法的準確性還有待提高。

表4給出了不同預緊順序下對應的螺栓平均殘余預緊力和殘余殘余預緊力標準差。對比圖4和表4可以看出，優化前，預緊順序①下螺栓的平均殘余預緊力稍大，但是殘余預緊力的標準差也大，即殘余預緊力分布不均勻；經四參數法預緊力優化后，兩種順序下平均殘余預緊力都大于目標預緊力，且殘余預緊力標準差明顯減小，預緊順序①下的平均殘余預緊力及殘余預緊力標準差依舊大于預緊順序②。

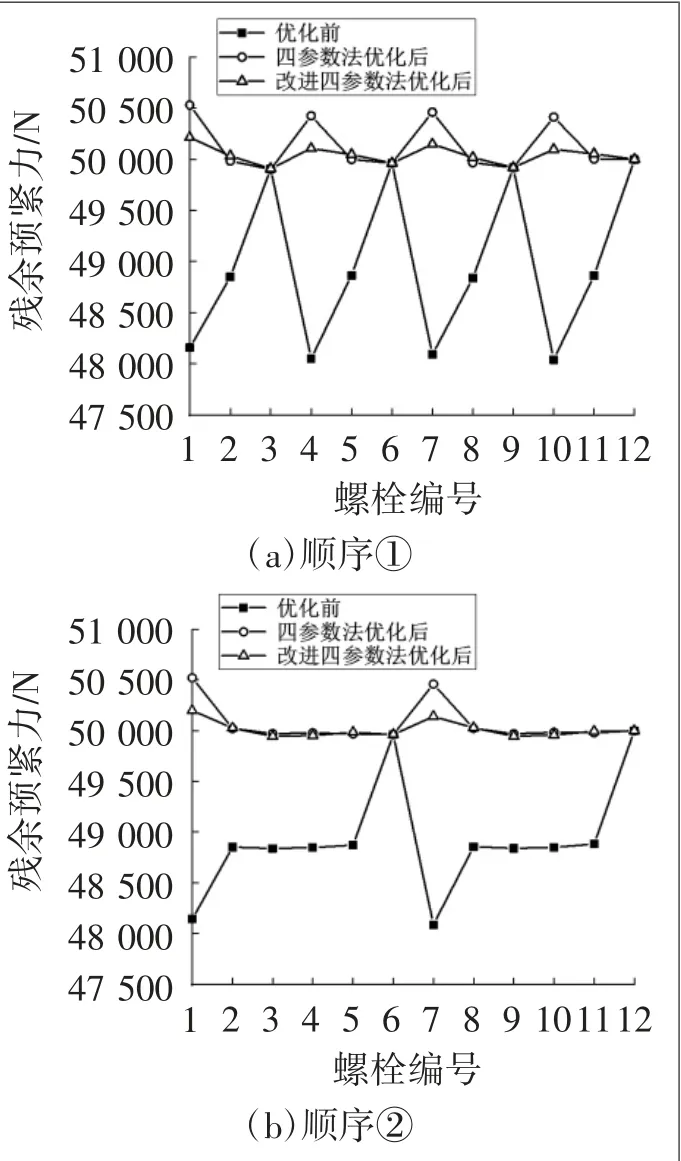
圖4 預緊力仿真結果

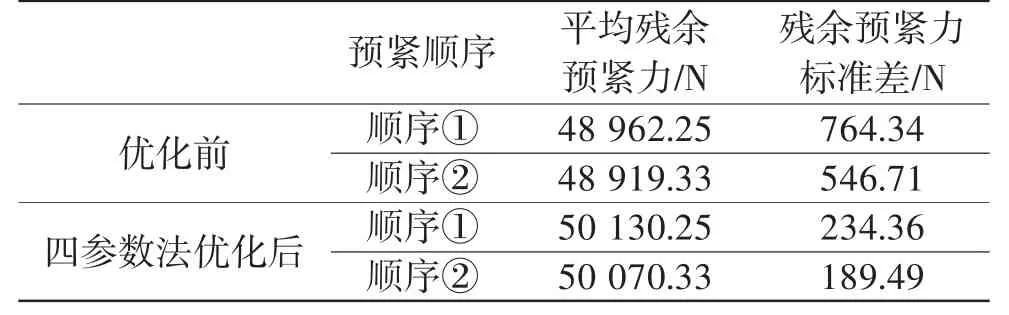
表4 平均殘余預緊力及預緊力標準差

3 改進四參數法

3.1 矩陣A參數計算方法的改進

上文說明了四參數法的基本原理、矩陣A中參數的計算方法和矩陣A的列出方法，并分析了優化后的螺栓平均殘余預緊力和殘余預緊力標準差，比優化前有了很大的提升，但是個別螺栓殘余預緊力依舊有較大分散性，原方法并未將螺栓b和c預緊的先后順序考慮在內，因為螺栓在裝配過程中是按照一定順序逐個預緊的，那么在預緊過程中一定會出現螺栓b先于螺栓c 預緊，或者螺栓c先于螺栓b預緊，進而導致參數β和δ出現兩種情況，如表5所示。

表5 參數β和δ兩種數值

從表5可以看出，由于螺栓b和c預緊先后順序的不同，導致參數β和δ分別出現了兩種數值，且相差較大。基于此，表6給出了改進后的參數計算方法，其中參數α和γ的計算方法與上文相同，此處不再表述。

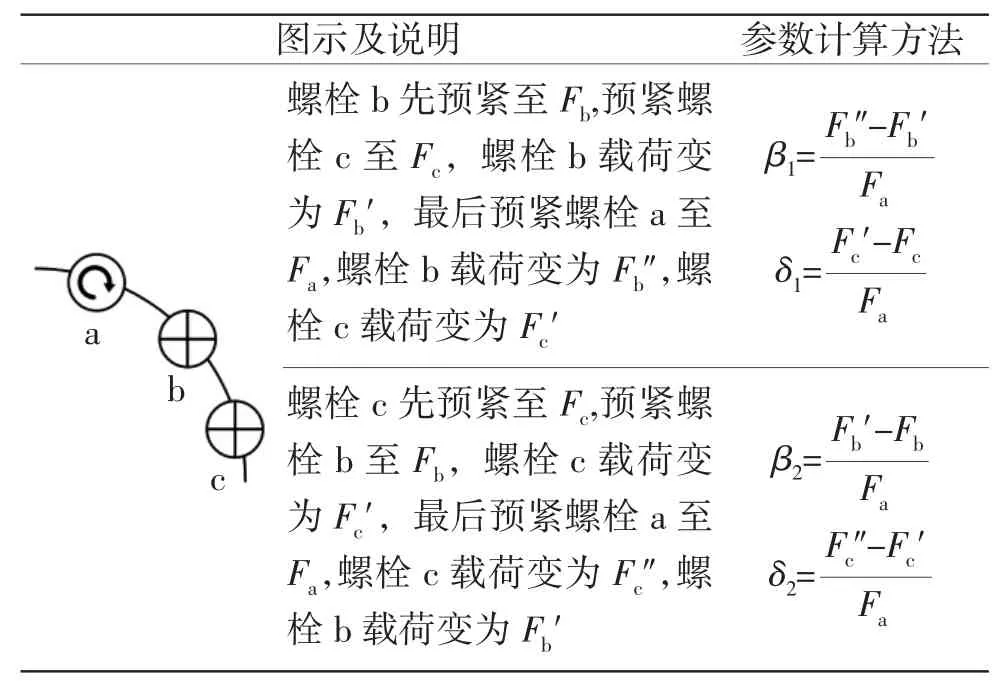
表6 參數計算方法的改進

3.2 結果分析

經改進四參數法計算出的參數及矩陣參考表2、表5和表3，此處不再贅述。

圖4給出了兩種預緊順序下的各螺栓預緊力分布情況。經改進四參數法優化后的螺栓殘余預緊力分布更加均勻，原本經四參數法優化后殘余預緊力大于目標預緊力的螺栓（即順序①中的1號、4號、7號和10號螺栓，順序②中的1號和7號螺栓），在經改進四參數法優化后更加接近目標預緊力，各螺栓的殘余預緊力分散程度進一步縮小。

表7給出了兩種順序下經改進四參數法優化后對應的螺栓平均殘余預緊力和殘余預緊力標準差。相對于四參數法，平均殘余預緊力更加接近目標預緊力，殘余預緊力標準差明顯減小，預緊順序①下，標準差減小了63%，預緊順序②下，標準差減小了59%。

表7 平均殘余預緊力及預緊力標準差

4 預緊順序及預緊力大小對結果的影響

為研究預緊順序和預緊力對結果的影響，采用順時針順序預緊（參考圖2）（即：1-2-3-4-5-6-7-8-9-10-11-12）和3種預緊力（即：10 000 N、30 000 N和50 000 N）進行計算，計算出的參數值如表8所示，對比表2和表5，3種預緊力下的參數值基本相等，這意味著同一個法蘭螺栓連接，預緊力的大小并不影響參數值的大小。

表8 參數值

圖6給出了順時針預緊順序下3種預緊力經修正四參數法優化后的仿真結果，可以看出，隨著目標預緊力的增大，殘余預緊力的分散程度明顯變大；對比圖5的順序①和順序②，目標預緊力50 000 N下，順時針順序的殘余預緊力分散程度明顯最小。

圖5 預緊力仿真結果

表9給出了順時針順序下3種平均殘余預緊力及殘余預緊力標準差，平均殘余預緊力均小于目標預緊力，殘余預緊力標準差隨著目標預緊力的增大而增大，即殘余預緊力分布越不均；對比表7，順時針順序下的標準差最小，順序②下的平均殘余預緊力最接近目標預緊力。

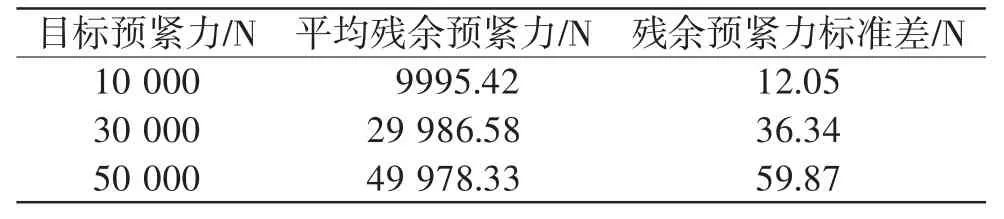
表9 平均殘余預緊力及殘余預緊力標準差

5 結論

1）基于四參數法對無墊片法蘭螺栓連接進行預緊力優化，優化后的平均殘余預緊力和殘余預緊力標準差相對于優化前都有較大提升；對四參數法進行改進，改進后的四參數法使平均殘余預緊力更加接近目標預緊力，標準差進一步縮小。

2）分析比較了預緊力和預緊順序對優化結果的影響。順時針順序下，不同預緊力計算出的矩陣A參數值是相同的，但是殘余預緊力標準差會隨著預緊力的增大而增大；在3種順序下，順時針順序下的標準差最小，順序②下的平均殘余預緊力最接近目標預緊力。