基于疲勞損傷的水庫混凝土重力壩抗震性優化研究

殷國竹,王興福,張孝永

(昭通漁洞水庫管理局,云南 昭通 657000)

0 引 言

作為傳統的大型水利水電建筑,重力壩的抗震性能一直是工程設計和建設過程中必須解決的重要問題[1]。因為地震是導致重力壩破壞的主要因素,一旦發生地震,重力壩將面臨著巨大的穩定性和安全性問題。采用科學合理的設計和加固措施,選擇優質的建筑材料,進行充分的模擬試驗和數值模擬,都是提高重力壩的穩定性和安全性的關鍵[2]。

本文以云南省昭通漁洞水庫為研究對象,考慮到重力壩受到的力的作用,構建混凝土重力壩線彈性動力模型;引入拉、壓損傷因子,構建混凝土塑性損傷模型;采用數值模擬方法,對該水庫重力壩抗震性進行研究,分析重力壩在地震波作用下受到的影響。通過試驗結果,給出相應的建議,提升重力壩的抗震性。研究結果可為有效提升重力壩的抗震性能提供參考與借鑒。

1 水庫混凝土重力壩損傷模型構建

1.1 混凝土重力壩線彈性動力模型構建

研究選擇云南省昭通漁洞水庫作為研究對象,該水庫位于昭通市西北23km的灑漁河上游居樂河上,是一座以農業灌溉為主,兼有發電、工礦和城市供水、向下游補水等綜合利用的大(Ⅱ)型水利工程。水庫樞紐從1992年開工建設,1996年下閘蓄水,2000年12月竣工驗收,水庫壩高87m,總庫容3.64×108m3。灌溉渠系于1996年開工建設,2003年自流灌溉區域的干支渠工程基本建成,控制灌溉面積1.56×104hm2,共建成干支渠264.1km。其中,干渠94.9km,新建支渠97.8km,改建支渠71.4km。

由于研究對象水流壓力大,因此應考慮自重、上下游靜水壓力、揚壓力、淤泥壓力和浪壓力問題。在保證重力壩結構極限承載能力狀態下,混凝土材料抗壓、抗拉強度公式如下:

(1)

式中:fkc為重力壩軸心抗壓強度標準值;γm為抗壓材料性能分布系數;γsc為承載能力極限狀態系數,在發生地震情況下,取值1.3。

非溢流壩是目前大型水流樞紐工程中的主要形式之一,由于水體壓力的作用,時刻都會受到水壓荷載的作用。非溢流壩有堆石壩和混凝土壩兩種形式,都會受到水重荷載和水體深度的影響[3]。水庫水位的變化也會引起壩體應力和應變的變化。此外,重力壩的揚壓力還會受到土壤的類型、水的深度、水的流速、壩底和側壁底部土層與地基情況的影響。土壤的孔隙結構會影響水壓力的傳遞方式,水的深度越深,水壓力也會越大。水的流速越大,其水壓力也會越大,導致揚壓力增大[4]。重力壩底部和側壁底部的土體受到水壓的作用后,整體會向上抬升,從而對壩體底部產生壓力。重力壩揚壓力的產生,會對壩體結構和地基結構產生較大的影響。如果揚壓力超過土體的承受能力,會導致土體的破壞和壩體的沉降。壓力分布圖見圖1。

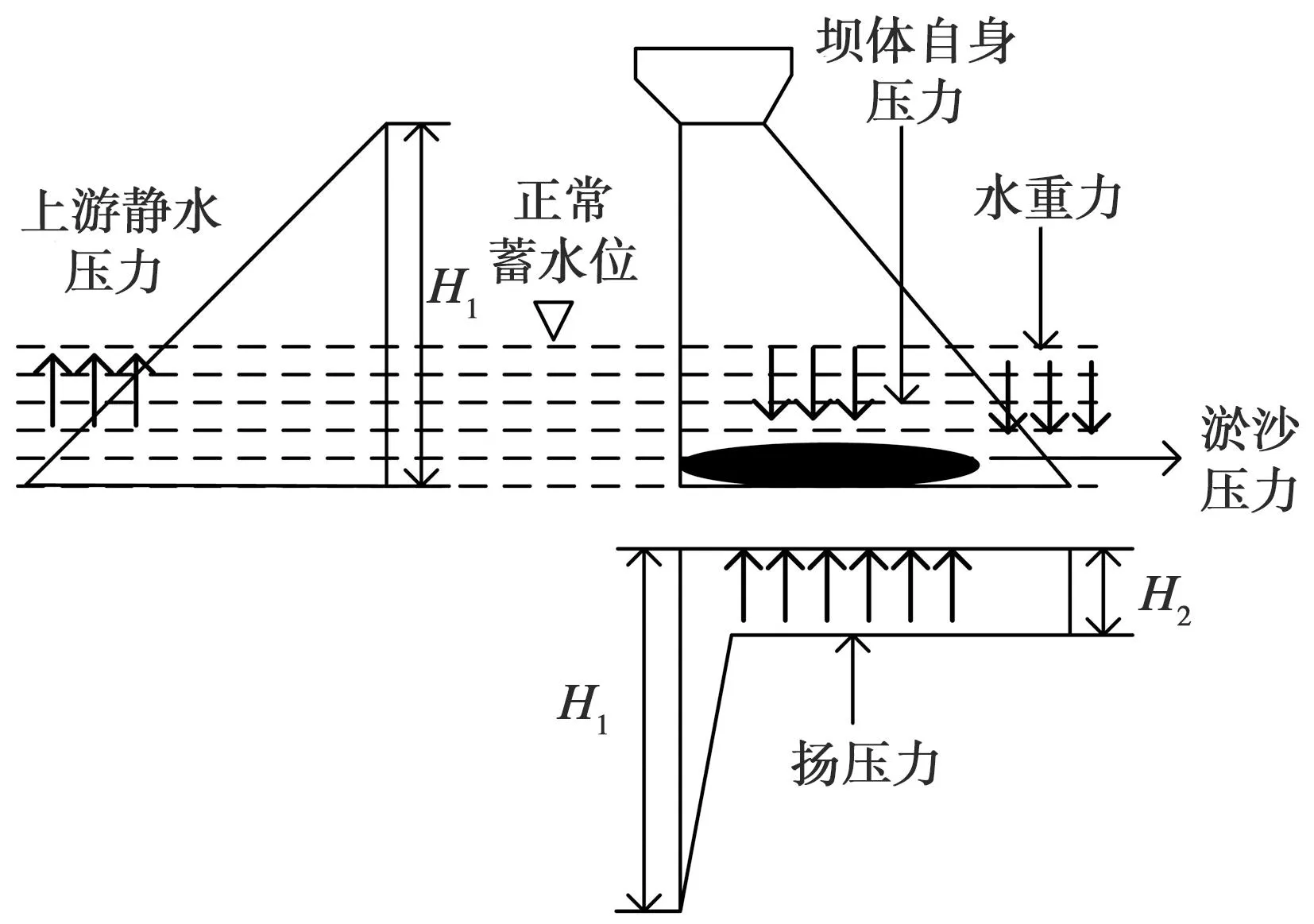
圖1 壓力在重力壩上的分布圖

由于云南省昭通漁洞水庫位于高原斷陷盆地、垅崗谷地貌、深蝕盆地、構造侵蝕低-中山地貌及構造侵蝕谷地貌,定時最大風速24m/s。在風速和地形的作用下,會產生浪壓力作用于重力壩表面。水波的高度和形狀、速度和方向、建筑物的大小和形狀都是影響浪壓力的因素。由于水庫中的水流動具有周期性和不規則性,會引起壩體的振動和破壞。浪壓力的壓力分布圖見圖2。

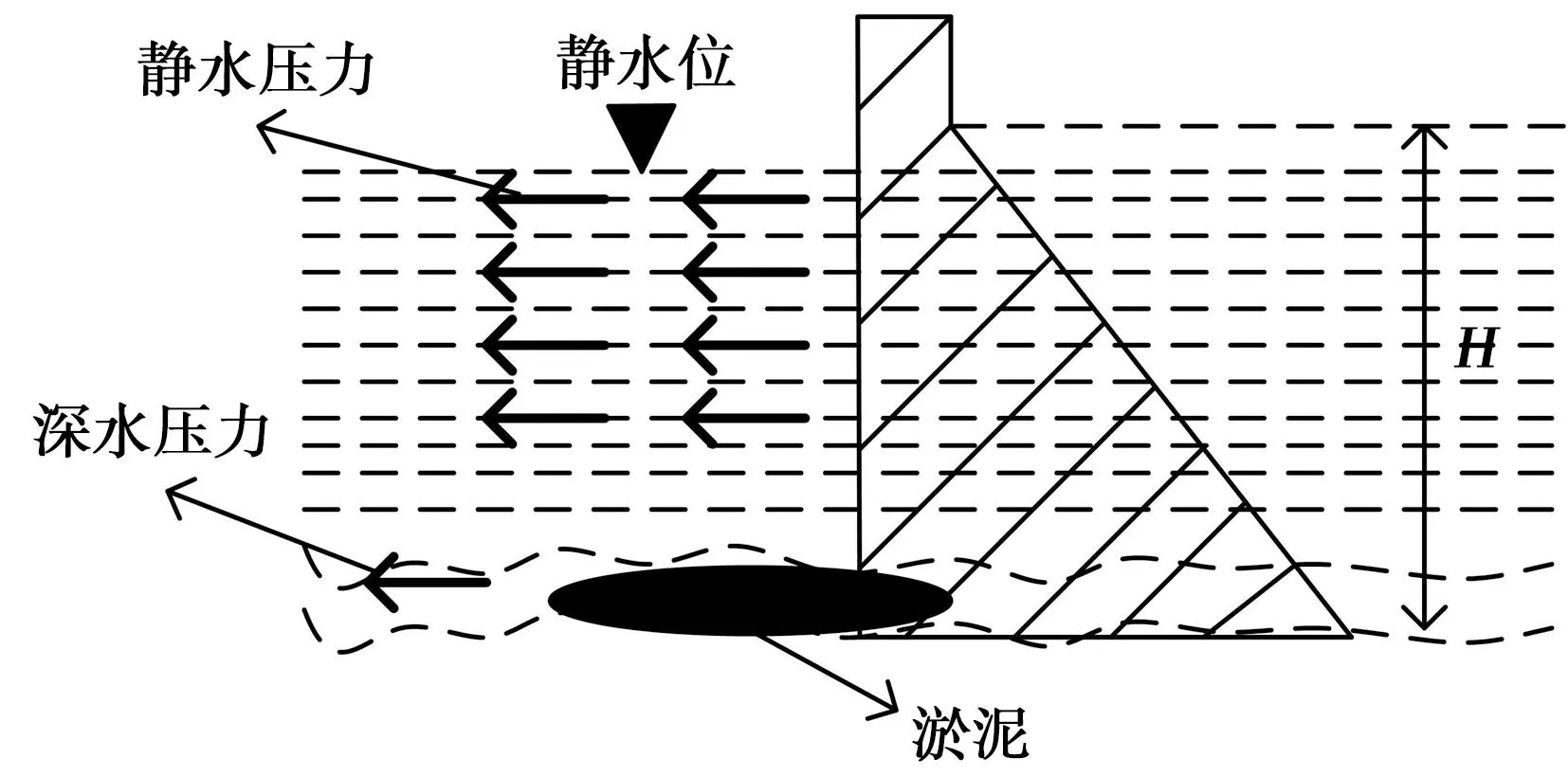
圖2 浪壓力在重力壩上的分布圖

由于云南省昭通漁洞水庫位于地震帶邊緣,地質構造主要有北東向灑漁河斷層和龍樹斷層、北西向尼古寨斷層,主要褶曲構造有北東向白莎背斜、小寨向斜、水磨向斜和北向新甸子向斜,因此會受到地震的影響。由于壩體中的壓力屬于非線性特征,采用紐馬克法對地震情況下的壩體進行計算分析,公式如下:

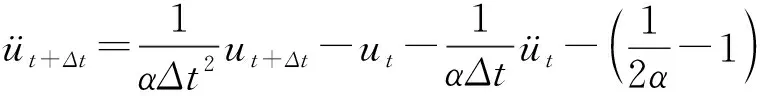
(2)

式中:α為保證積分精確度而引入的系數;t為時間;ut、ut+Δt分別為t和t+Δt的位移解;üt為t時間的速度;üt、üt+Δt分別為t時刻和t+Δt時刻的加速度。

當地震作用在水庫重力壩上時,會造成重力壩頂端發生相對位移。

1.2 混凝土塑性損傷模型構建

地震下混凝土重力壩的疲勞損傷破壞,是由于壩體長期受到地震作用。當重力壩受到震動或地震荷載作用時,內部混凝土也會發生應變和位移變化,引起微小的損失。當重復受到震動或地震荷載時,這些混凝土內部產生的微小損傷逐年累積,導致混凝土的內部強度和韌性下降,最終引起疲勞損傷[5]。混凝土在低應力范圍內呈線性彈性的特征,但在高應力范圍內,呈非線性的本質特征。在混凝土結構被破壞前的非線性階段,稱為“軟化階段”,該階段內的應力逐漸降低,應變增加[6]。

由于混凝土的制作工藝不同、材料本身的差異性,導致內部某些部分存在明顯的大顆粒或含氣孔等缺陷。這些缺陷導致混凝土在壓縮和拉伸等不同的應力狀態下,表現出不同的剛度。混凝土的應力應變分為單軸和多軸,單軸應力應變只有一個方向受到應力作用的情況,多軸應力應變是同時受到多個方向作用的應力的情況[7]。混凝土的拉伸和壓縮應力狀態下的應變曲線圖見圖3。

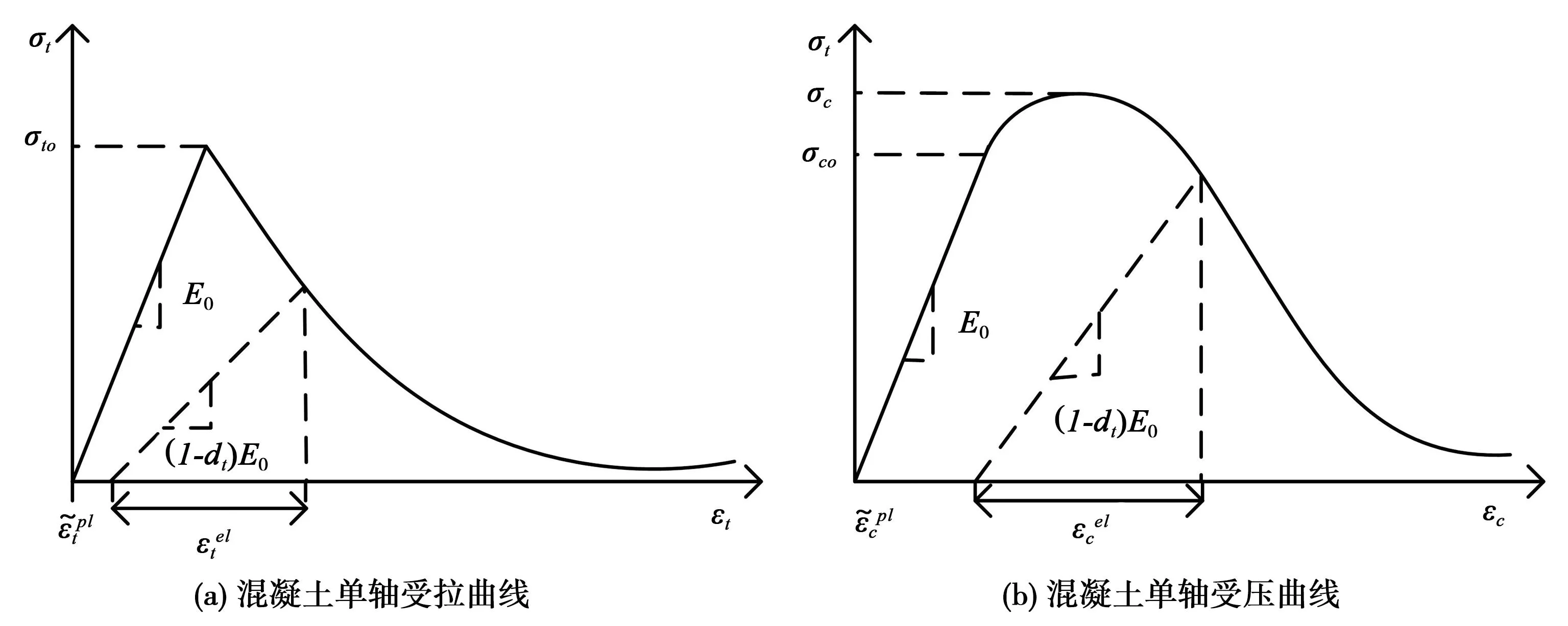
圖3 混凝土的拉伸和壓縮應力狀態下的應變曲線圖

在單軸應力作用下,混凝土的應變量在應力較小的階段,呈現出一定的線性關系。當應力達到一定程度后,混凝土的應變量和應力之間便不再為固定的線性關系,而是逐漸呈現出一種偏向不規則性。此時,混凝土逐漸開始發生裂紋,產生非彈性變形[8]。裂紋是混凝土損傷中最常見的表現形式,裂縫可分為兩種類型:①裂縫間隔較大,寬度較窄的彈性裂縫;②間隔較小,寬度較大的鏈式裂縫。

在多軸應力作用下,混凝土中的應變量呈現更加復雜的關系[9]。除了單軸應力下的彈性變形、塑性變形和頹塌外,還會引發多軸的非比例變形。因此,當混凝土受到多個方向的應力時,會以一種非等向性的方式產生彈性變形。彈性變形的方向是隨著應力的大小和方向而發生的微小變化。

為了進一步更準確地描述混凝土的非線性特征,采用混凝土塑性損傷模型。混凝土塑性損傷模型能對混凝土內部的應力應變狀態以及變形狀態進行定量分析,確定混凝土的破壞機理。為了更好地對重力壩混凝土的受力情況進行分析,在混凝土塑性損傷模型中,引入拉、壓損傷因子。混凝土發生損傷后的應力應變公式如下:

(3)

在地震力對壩體循環荷載的作用下,利用公式計算應力狀態是否進入塑性狀態。當混凝土受到損傷,進入塑性狀態時,將多軸應力應變轉換為單軸應力應變,得到等效的塑性應變。引入的損傷因子能通過計算混凝土內部的斷裂面積占總體面積的比值,來判斷混凝土損傷的情況,以此來反映剛度退化。而剛度退化可以用來描述由于內部裂縫和裂隙,導致混凝土承載能力下降和剛度的減少情況,對于混凝土的結構設計和維護均有重要的意義。

2 實際案例分析

研究以云南省昭通漁洞水庫作為算例,采用混凝土塑性損傷模型,通過地震循環荷載的方式,使混凝土重力壩逐漸達到極限狀態。該水庫最大高度87m,淤泥浮容重為5kN/m3,淤沙摩擦角為5°,混凝土容重取14kN/m3,水的容重取9.81kN/m3,基巖的密度為2 775kN/m3。混凝土和基巖的物理參數見表1。

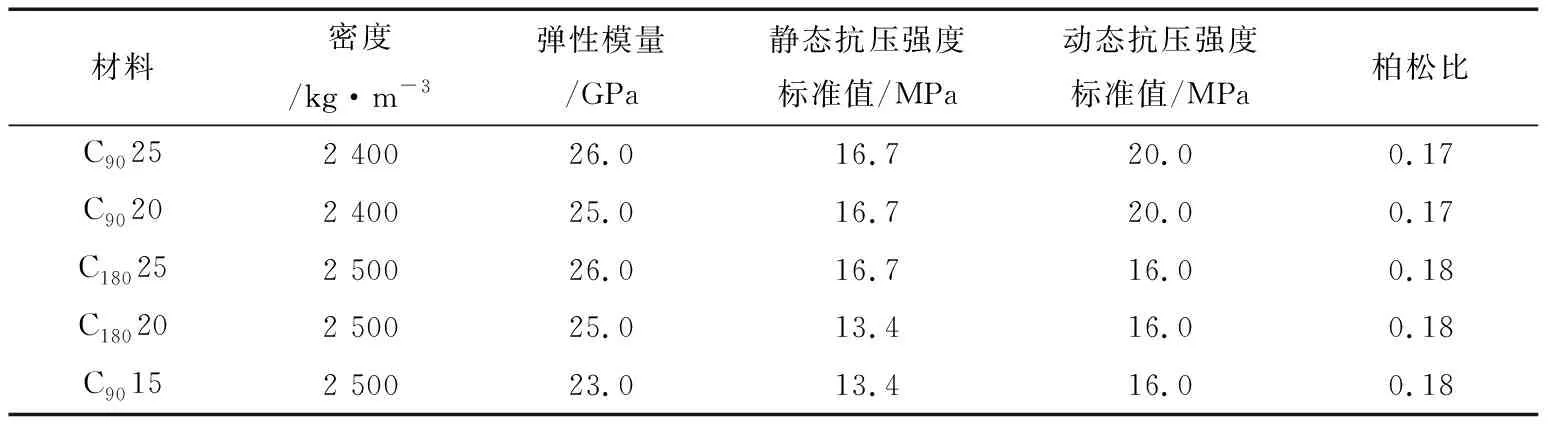
表1 混凝土和基巖的物理參數表

設置水流順下游流動的方向為X軸,水流指向右岸的方向為Y軸,鉛垂水流的方向為Z軸。由于壩踵位置受到各種力的作用較強,而重力壩的重心高于壩頂,因此位移主要出現在壩頂位置。選取壩頂部位的一個特征點進行位移分析,地震波震級設置為3級,持續時間設置為40s。X、Y、Z方向的位移時程曲線見圖4。

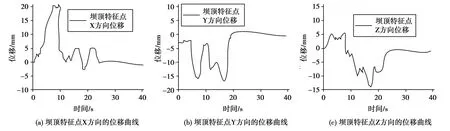
圖4 壩頂特征點朝不同方向位移曲線圖

圖4為重力壩X、Y、Z軸方向發生位移的曲線圖。由于地震波的傳播過程是一個不斷能量轉化和損耗的過程,因此隨著距離的增加而逐漸減弱,橫波和縱波對于重力壩體的影響逐漸減小。由圖4(a)可知,隨著時間的增長,壩頂特征點X方向位移量增加,在10s時達到峰值,此時的位移量為20mm。24s后X方向的位移量趨于平衡,此時特征點幾乎沒有發生X軸方向上的偏移。由圖4(b)可知,在試驗剛開始5s內,重力壩頂部特征點維持在朝左岸3mm位移量左右;在8s時,達到第一個位移峰值,此時的位移量為16mm;當20s時,重力壩體回到正常位置,位移量為0mm;20s后,位移量基本保持不變,趨于穩定狀態。由圖4(c)可知,在試驗開始的8s內,壩頂特征點朝Z軸正向位移平均值為5mm;8s后,特征點朝Z軸反向開始偏移;在17s時達到反向位移峰值,此時的位移量為14mm;在17s后,特征點位移量逐漸回到原始值;20s后的位移量幾乎沒有變化,維持在原始狀態。

選擇人造地震波Koyna地震波,對壩踵特征點的順河向位移時程、豎直河向位移時程、順河向應力時程、豎直河向應力時程進行分析,時程曲線圖見圖5。

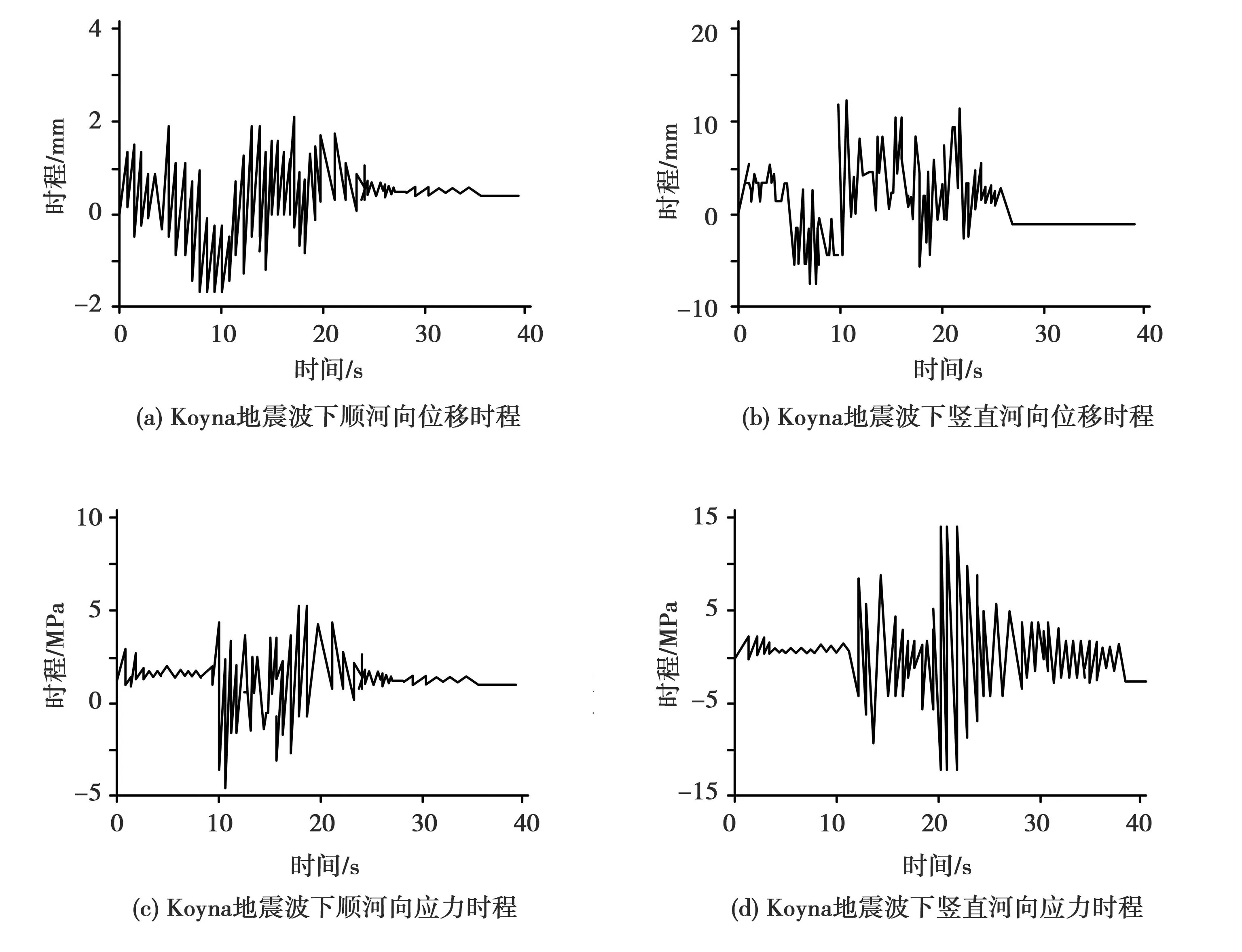
圖5 Koyna地震波下的位移和應力時程曲線

圖5(a)為Koyna地震波下,壩踵特征點順河向位移時程。在試驗開始前5s內,特征點順河向時程在-0.2～1.2mm之間擺動。5～10s時間內,特征點順河向時程逐漸增大,達到-1.8mm時程量;10s后,特征點順河向位移反向增大;在16s時達到峰值,此時的時程值為2.1mm。圖5(b)為Koyna地震波下,壩踵特征點豎直河向位移時程。在試驗開始前5s內,特征點豎直河向位移基本保持不變;在8s時達到第一個峰值,此時的位移時程為-7.2mm;在12s時達到第二個峰值,此時的位移時程為12mm;在20s時,位移時程為-4.8mm;25s后,位移時程基本保持穩定。圖5(c)為Koyna地震波下,壩踵特征點順河向應力時程。在試驗開始10s內,應力時程保持在1.2～1.3MPa范圍內;在10s時達到第一個峰值,此時的應力時程為-4.8MPa;10s后,應力時程減小;在25s后,應力時程基本保持不變。圖5(d)為Koyna地震波下,壩踵特征點豎直河向應力時程。在試驗開始的10s內,應力時程基本保持不變;在20s后,應力時程在-11.5～13.5MPa之間擺動;在25～40s時間段內,應力時程保持在-2.5～2.5MPa之間。可以看出,此時壩體的應力比較集中,主要受到豎直向應力的影響,壩體開始出現損傷。因此,應對壩體的壩踵部位進行加固,避免出現壩體進一步的損壞。

為了進一步探討壩踵承受地震荷載作用的大小,對壩踵上特征點在不同超載系數下的時程內最大相關變量進行分析,測試結果見表2。

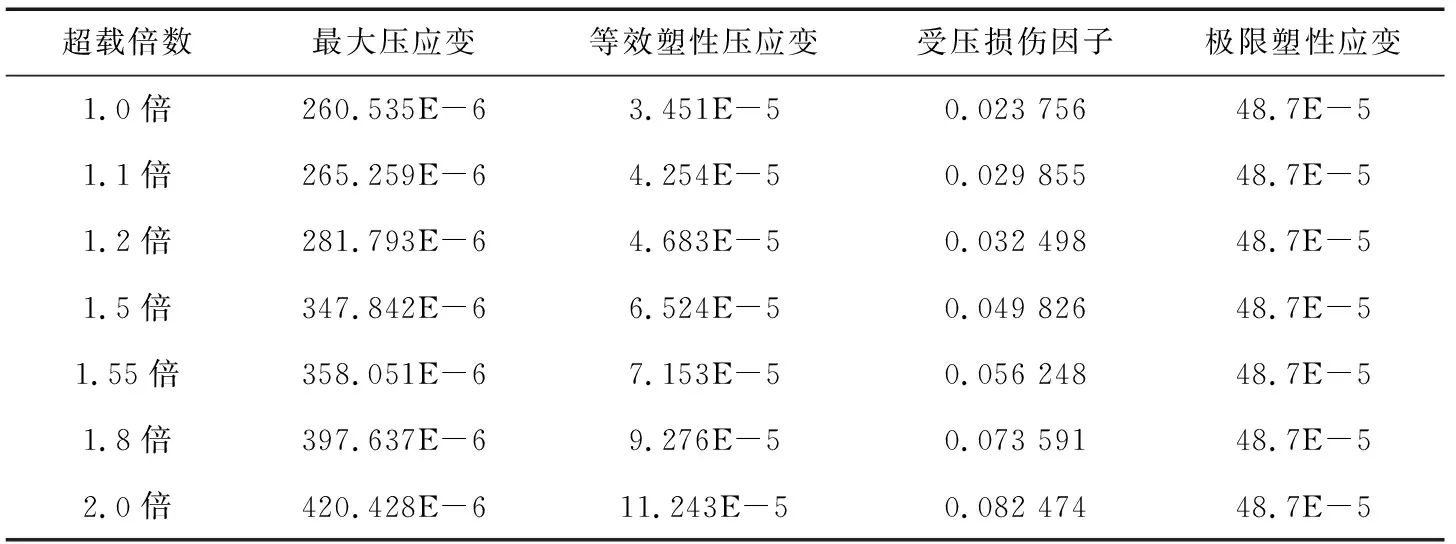
表2 壩踵上特征點在時程內的最大相關變量值表

由表2可知,在1.0倍地震超載時就出現了受壓損傷,在2.0倍條件下壩體受到的損傷大于1.0倍時的損傷,但此時的壩體也并未達到極限塑性應變值,混凝土材料承載能力并沒有減弱。

為了增強壩體的穩定性,加入齒墻進行分析。齒墻的作用能保證重力壩在外力的作用下不發生滑移,使得壩體整體的穩定性更強。研究齒墻寬度對壩基面應力的影響,設置齒墻寬度為5和20m,將沒有齒墻的壩基面應力值與設置齒墻的壩基面應力值相比較。不同齒墻寬度下的壩基面應力值見圖6。

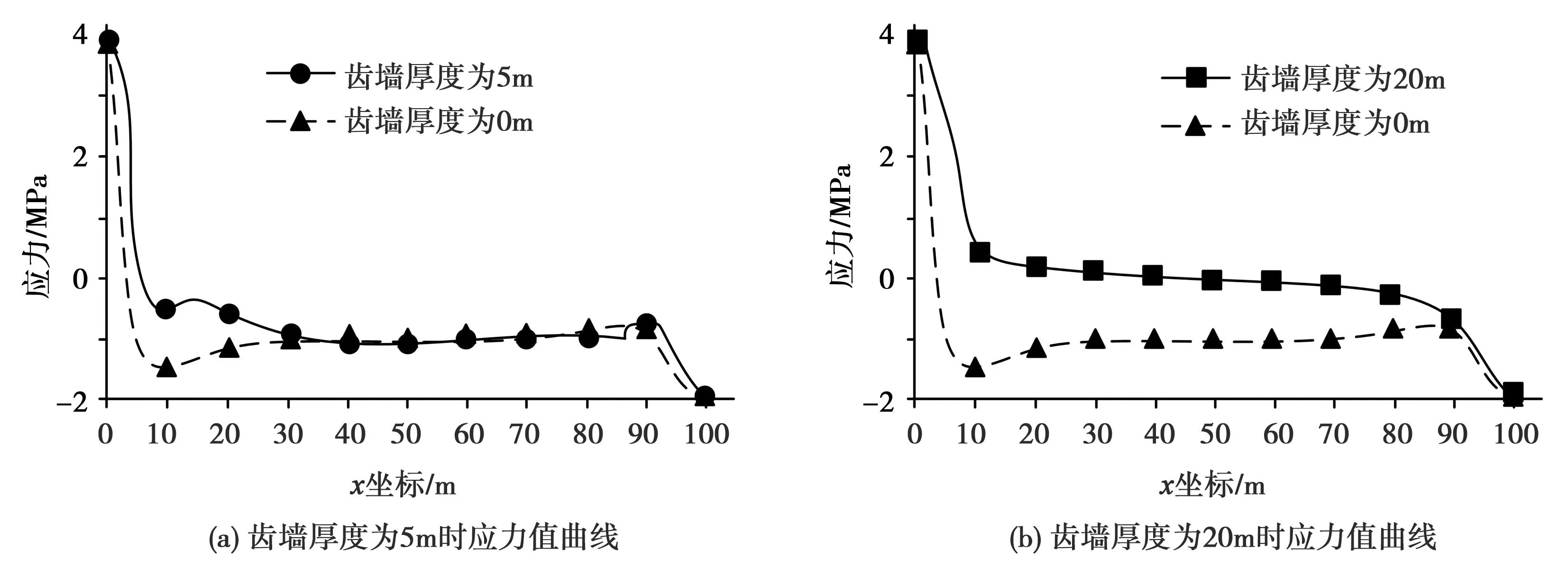
圖6 不同齒墻厚度下的應力值曲線圖

圖6(a)和圖6(b)中,隨著齒墻厚度的增加,應力值都存在減小的情況。由于壩基面承受著壩體全部的重力和外界力的作用,應力明顯集中于壩踵處,因此受到的應力作用最大。壩體中部受到的應力作用相較于壩踵處有所減小,壩頂應力值最小。齒墻的存在能夠減小應力集中的情況,隨著齒墻厚度的增加,對應力減小的作用更大。當齒墻厚度為5m時,受到的應力相較于無齒墻時減小1.25%;當齒墻厚度為20m時,受到的應力相較于無齒墻時減小3.48%。因此,適量增加齒墻的厚度,有助于加強重力壩的穩定性。

3 結 論

本文采用構建的混凝土重力壩線彈性動力模型和塑性損傷模型,對云南省昭通漁洞水庫重力壩進行了數值模擬分析。結果表明,壩頂部位主要受到拉力的作用,壩踵主要受到豎直向應力的作用,使特征點發生了位移。在2.0倍地震超載情況下,壩體受損較嚴重,但并未達到極限塑性應變值。設置齒墻寬度為5和20m,其中20m齒墻寬度時,壩基面應力值最小。