含平方阻尼項(xiàng)的Mathieu-Duffing系統(tǒng)混沌與分岔研究

解加全, 王海軍, 師 瑋, 張佳樂, 霍逸婷, 曹佳琳, 高 薔

(1. 太原師范學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 山西 晉中 030619;2. 太原師范學(xué)院 智能優(yōu)化計(jì)算與區(qū)塊鏈技術(shù)山西省重點(diǎn)實(shí)驗(yàn)室, 山西 晉中 030619;3. 太原理工大學(xué) 機(jī)械與運(yùn)載工程學(xué)院, 太原 030024)

Mathieu-Duffing方程是Mathieu方程和Duffing方程的結(jié)合和合并,Duffing方程是描述共振現(xiàn)象、調(diào)和振動(dòng)、次調(diào)和振動(dòng)、擬周期振動(dòng)、概周期振動(dòng)、奇異吸引子和混沌現(xiàn)象的簡(jiǎn)單數(shù)學(xué)模型,Duffing 方程在船舶橫搖、微弱信號(hào)檢測(cè)、振動(dòng)能量采集等問題中被廣泛應(yīng)用[1-5]。Mathieu方程作為 Hill 方程一種特殊形式,是一種含參數(shù)激勵(lì)的線性振動(dòng)模型,經(jīng)常被用來處理一些參數(shù)共振現(xiàn)象,在參激振動(dòng)研究中得到了廣泛的應(yīng)用[6-9]。工程實(shí)際中的許多非線性振動(dòng)問題的數(shù)學(xué)模型都可以轉(zhuǎn)化為Mathieu-Duffing方程來研究,如醫(yī)學(xué)、脈沖爆炸現(xiàn)象、信號(hào)檢測(cè),船的橫搖運(yùn)動(dòng)、結(jié)構(gòu)振動(dòng)、化學(xué)鍵的破壞等[10-14]。侯東曉等[15]利用多尺度法求解一類具有Mathieu-Duffing振子的兩質(zhì)量相對(duì)轉(zhuǎn)動(dòng)系統(tǒng)發(fā)生主共振-基本參數(shù)共振的分岔響應(yīng)方程。牛江川等[16]研究了含分?jǐn)?shù)階微分項(xiàng)的Mathieu-Duffing振子在簡(jiǎn)諧激勵(lì)下的亞諧共振。邢真慈等[17]運(yùn)用多尺度方法研究了參數(shù)激勵(lì)下帶有時(shí)滯反饋的隨機(jī)Mathieu- Duffing方程的主參數(shù)共振響應(yīng)問題。沈建和等[18]研究了Mathieu-Duffing振子混沌軌道至任意目標(biāo)周期軌道的控制問題。

自 1963年Lorenz發(fā)現(xiàn)第一個(gè)混沌吸引子以來,混沌理論得到了迅猛的發(fā)展,18世紀(jì)以來,科學(xué)家對(duì)天體力學(xué)、流體力學(xué)和非線性振動(dòng)中的一些失穩(wěn)現(xiàn)象的研究發(fā)現(xiàn)了分岔現(xiàn)象,分岔和混沌也是非線性科學(xué)領(lǐng)域重要的研究?jī)?nèi)容,在圖像處理、保密通信、計(jì)算機(jī)網(wǎng)絡(luò)、金融系統(tǒng)、信號(hào)處理、交通、生命科學(xué)等領(lǐng)域取得了迅猛發(fā)展和廣泛應(yīng)用[19-24]。馮進(jìn)鈐等[25]證明了隨機(jī)Duffing單邊約束系統(tǒng)同樣存在豐富的倍周期分岔現(xiàn)象。樓京俊等[26]研究了多頻激勵(lì)下的軟彈簧型 Duffing系統(tǒng)的混沌動(dòng)力學(xué)。朱為國(guó)等[27]研究在溫度場(chǎng), 機(jī)械場(chǎng)與電磁彈性耦合作用下四邊固定支撐矩形薄板的分岔與混沌運(yùn)動(dòng)問題。馬少娟等[28]應(yīng)用Laguerre正交多項(xiàng)式逼近法研究了含有隨機(jī)參數(shù)的雙勢(shì)阱Duffing系統(tǒng)的分岔和混沌行為。振動(dòng)共振現(xiàn)象由Landa和McClintock首次提出,目前已經(jīng)有部分學(xué)者對(duì)振動(dòng)共振現(xiàn)象進(jìn)行了研究。例如,Yang等[29]研究了具有分?jǐn)?shù)階位勢(shì)非線性的過阻尼系統(tǒng)的振動(dòng)共振。彭榮榮[30]運(yùn)用多尺度法研究了一類含有外激力和五次非線性恢復(fù)力的Duffing系統(tǒng)。李欣業(yè)等[31]運(yùn)用平均法研究了Duffing-Van der Pol振子的主參數(shù)共振響應(yīng)及其時(shí)滯反饋控制問題。在現(xiàn)代航海中,輪船受到風(fēng)浪的影響,會(huì)左右橫搖,嚴(yán)重時(shí)會(huì)使輪船傾覆。郭建斌等[32]在對(duì)船舶橫搖運(yùn)動(dòng)研究中,使用平方阻尼Mathieu振子作為模型并加入分?jǐn)?shù)階項(xiàng),提供減震思路。

綜上所述,本文利用多尺度法研究了平方阻尼的Mathieu-Duffing 振子在簡(jiǎn)諧激勵(lì)下的主共振響應(yīng),建立主共振幅頻響應(yīng)方程的解析表達(dá)式,對(duì)定常解的穩(wěn)定性進(jìn)行分析,應(yīng)用 Melnikov 方法得到系統(tǒng)進(jìn)入Smale馬蹄意義下混沌的條件,通過數(shù)值仿真分析了系統(tǒng)不同參數(shù)對(duì)混沌運(yùn)動(dòng)的影響,所得結(jié)果為抑制混沌運(yùn)動(dòng)的研究方向提供了理論驗(yàn)證。

1 近似解析解

在船舶橫搖中研究如下含有平方阻尼的Mathieu-Duffing振子模型

(1)

對(duì)系統(tǒng)作如下變量替換

ε=β/m,2ε=γ/m,f1=F/m

式中:ε為小參數(shù);ω0為系統(tǒng)的無阻尼固有頻率。則式(1)可以轉(zhuǎn)換為

(2)

為研究系統(tǒng)的主共振情況,要求ω≈ω0,且f1為小量,即

f1=εf,ω=ω0+εσ,f=O(1),σ=O(1)

其中,σ為引入的調(diào)諧因子,則式(2)可以轉(zhuǎn)換為

(3)

應(yīng)用多尺度法研究系統(tǒng)的一次近似解,引入兩個(gè)時(shí)間尺度T0=t,T1=εt,并假設(shè)式(3)的解具有如下形式

u(t;ε)=u0(T0,T1)+εu1(T0,T1)

(4)

將式(4)代入式(3),比較ε的同次冪,得到一組偏微分方程組

(5)

式(5)的解為

u0(T0,T1)=a(T1)cos[ω0T0+η(T1)]

(6)

式中,a(T1)和η(T1)分別為慢變振幅和相位。

式(7)也可以寫成復(fù)數(shù)形式

u0(T0,T1)=A(T1)eiω0T0+cc

(7)

(8)

(9)

(10)

其中

(11)

引入

(12)

(13)

(14)

系統(tǒng)的一次近似解為

u(t)=acos(ω0T0+η)=acos(ω0T+σT1+φ)=
acos(ωt+φ)

(15)

式中,a和φ由式(14)和式(15)確定。

2 定常解及其穩(wěn)定性

(16)

(17)

進(jìn)一步可以從式(17)和式(18)推導(dǎo)出穩(wěn)態(tài)運(yùn)動(dòng)的幅頻響應(yīng)方程和相頻響應(yīng)方程分別為

(18)

(19)

下面利用Lyapunov第一方法考察定常解的穩(wěn)定性,定義狀態(tài)向量V=[a,φ]T,利用式(14)和式(15)構(gòu)造向量函數(shù)

(20)

(21)

λ2-Pλ+Q=0

(22)

式中,P=trJ,Q=det[J]。

處漸近穩(wěn)定的條件是P<0且Q>0,因此系統(tǒng)的穩(wěn)態(tài)響應(yīng)在Lyapunov意義下的穩(wěn)定性條件為

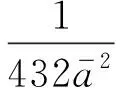
(23)

3 混沌運(yùn)動(dòng)的Melnikov條件

在此考慮系統(tǒng)剛度軟化的情況(α1<0),對(duì)式(1)進(jìn)行如下坐標(biāo)變換

ευ=γ/m,δε=F/m,ε=β1/m

其中ε為小參數(shù),從而式(1)可以寫成

(24)

將式(25)寫成狀態(tài)方程形式

(25)

(26)

當(dāng)ε=0時(shí),未擾系統(tǒng)為Hamilton系統(tǒng)

(27)

(28)

其Hamilton量為

(29)

勢(shì)函數(shù)為

(30)

由于

(31)

(32)

(33)

(34)

(35)

將式(25)寫成向量函數(shù)的形式

(36)

則受擾系統(tǒng)(25)的Melnikov函數(shù)為

(37)

整理得

(38)

從而根據(jù)Melnikov定理可知,系統(tǒng)出現(xiàn)異宿軌道橫截相交的必要條件是

(39)

4 數(shù)值仿真

為了驗(yàn)證近似解析解的正確性,選取一組參數(shù),根據(jù)式(14)和式(15)得到系統(tǒng)幅頻響應(yīng)曲線。圖1顯示數(shù)值解與解析解在振動(dòng)形式上是一致的,其幅值均出現(xiàn)了跳躍現(xiàn)象,表明解析解與數(shù)值解有很高的擬合度。

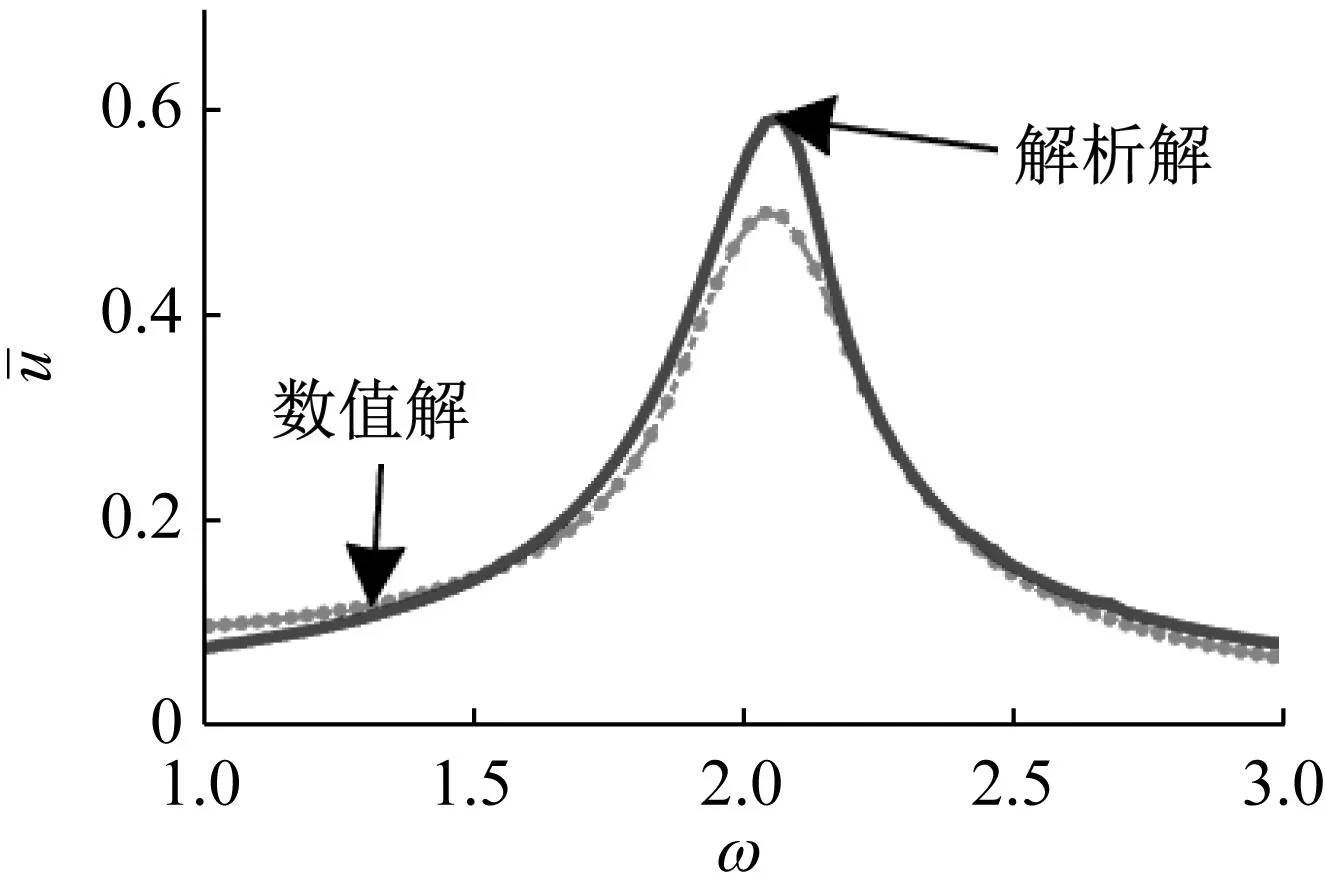
圖1 幅頻曲線對(duì)比,其他計(jì)算參數(shù)為m=1;k=4;c=0.2;α1=0.7; γ=0.7;F=0.3;β=0.3;μ1=0.4;μ2=0.3Fig.1 Amplitude-frequency curve comparison, other calculation parameters are m=1;k=4;c=0.2;α1=0.7;γ=0.7;F=0.3; β=0.3;μ1=0.4;μ2=0.3

由式(19)計(jì)算定常解的幅頻特性,再由式(24)判斷對(duì)應(yīng)解支的穩(wěn)定性,得到定常解的幅頻特性曲線如圖2所示。由于系統(tǒng)同時(shí)受到強(qiáng)迫激勵(lì)和參數(shù)激勵(lì)的聯(lián)合作用,導(dǎo)致系統(tǒng)至多存在3個(gè)周期解支,其中1支為穩(wěn)定解,2支為不穩(wěn)定解。

圖2 定常解的幅頻響應(yīng),其他計(jì)算參數(shù)為m=1;k=0.4;c=0.01; α1=0.05;γ=0.2;F=0.01;β=0.1;μ1=0.01;μ2=0.01Fig.2 The amplitude-frequency response of the steady solution, other calculation parameters are m=1;k=0.4;c=0.01;α1=0.05;γ=0.2;F=0.01;β=0.1;μ1=0.01;μ2=0.01

圖3給出非線性阻尼取不同值的幅頻曲線,可以清晰的看到隨著非線性阻尼的增大,系統(tǒng)總響應(yīng)的幅值減小,由此說明本系統(tǒng)中非線性阻尼項(xiàng)的存在對(duì)系統(tǒng)振動(dòng)起抑制作用,取值愈大抑制愈強(qiáng)。

圖3 不同非線性阻尼的幅頻曲線,其他參數(shù)為m=1;k=4;c=0.2; α1=0.7;γ=0.7;F=0.3;β=0.3Fig.3 Amplitude-frequency curves with different nonlinear damping, and other calculated parameters are m=1;k=4; c=0.2;α1=0.7;γ=0.7;F=0.3;β=0.3

選取激勵(lì)頻率ω作為分岔參數(shù),選取一組參數(shù),根據(jù)數(shù)值解得到ω∈[0,1]系統(tǒng)的分岔圖,如圖4所示。隨著激勵(lì)頻率ω變化,系統(tǒng)發(fā)生了倍周期分岔,且系統(tǒng)中間交替發(fā)生多次的倍周期分岔。

圖4 激勵(lì)頻率ω的全局分岔圖,其他計(jì)算參數(shù)為m=0.5;k=0.02; c=0.02;γ=1.2;α1=0.2;β=0.3;μ1=0.05;μ2=0.05; F=0.05Fig.4 The global bifurcation diagram of excitation frequency ωand other calculation parameters are m=0.5;k=0.02;c=0.02; γ=1.2;α1=0.2;β=0.3;μ1=0.05;μ2=0.05;F=0.05

圖5給出系統(tǒng)在ω=0.8時(shí)的Poincare截面圖,由圖知當(dāng)ω=0.8時(shí),Poincare 截面有一個(gè)吸引點(diǎn), 因此系統(tǒng)是一個(gè)典型的單周期運(yùn)動(dòng)。

圖5 ω=0.8的Poincare截面,其他計(jì)算參數(shù)為 m=0.5;k=0.02; c=0.02;γ=1.2;α1=0.2;β=0.3;μ1=0.05;μ2=0.05;F=0.05Fig.5 The Poincare cross section when ω=0.8, and other calculated parameters are m=0.5;k=0.02;c=0.02;γ=1.2; α1=0.2;β=0.3;μ1=0.05;μ2=0.05;F=0.05

圖6給出系統(tǒng)在ω=0.09時(shí)的Poincare截面圖,相軌跡在有界區(qū)域內(nèi)反復(fù)纏繞而不封閉,Poincare截面非有限點(diǎn)集,非封閉曲線,具有明顯的分形結(jié)構(gòu),以上特征均說明此時(shí)系統(tǒng)處于混沌狀態(tài)。

圖6 ω=0.09的Poincare截面,其他計(jì)算參數(shù)為m=0.5;k=0.02; c=0.02;γ=1.2;α1=0.2;β=0.3;μ1=0.05;μ2=0.05;F=0.05Fig.6 The Poincare cross section when ω=0.09, and other calculated parameters are m=0.5;k=0.02;c=0.02;γ=1.2; α1=0.2;β=0.3;μ1=0.05;μ2=0.05;F=0.05

選取激勵(lì)幅值F作為分岔參數(shù),選取一組參數(shù),由數(shù)值解得到F∈[0.04,1]系統(tǒng)分岔密度分布圖,如圖7所示。隨著激勵(lì)幅值F變化,系統(tǒng)發(fā)生倍周期分岔,系統(tǒng)從 1-1 單周期發(fā)生倍周期分岔轉(zhuǎn)遷為混沌運(yùn)動(dòng),且系統(tǒng)中間交替發(fā)生多次的倍周期分岔,最終回歸到周期運(yùn)動(dòng)。

圖7 激勵(lì)幅值F的分岔密度分布圖,其他計(jì)算參數(shù)為m=1;k=0.02; c=0.04;γ=0.2;α1=0.2;β=0.3;μ1=0.05;μ2=0.05; ω=0.09Fig.7 Bifurcation density distribution diagram of excitation amplitude F, and other calculation parameters are m=1;k=0.02;c=0.04;γ=0.2;α1=0.2;β=0.3;μ1=0.05; μ2=0.05;ω=0.09

圖8給出系統(tǒng)在F=0.4時(shí)的Poincare截面圖,由圖知當(dāng)F=0.4時(shí), Poincare 截面有一個(gè)吸引點(diǎn),系統(tǒng)是一個(gè)典型的單周期運(yùn)動(dòng)。

圖8 F=0.4的Poincare截面,其他計(jì)算參數(shù)為 m=1;k=0.02; c=0.04;γ=0.2;α1=0.2;β=0.3;μ1=0.05;μ2=0.05;ω=0.09Fig.8 The Poincare cross section when F=0.4, and other calculated parameters are m=1;k=0.02;c=0.04;γ=0.2; α1=0.2;β=0.3;μ1=0.05;μ2=0.05;ω=0.09

圖9給出系統(tǒng)在F=0.093時(shí)的Poincare截面圖。相軌跡在有界區(qū)域內(nèi)反復(fù)纏繞回旋而不封閉,Poincare截面非有限點(diǎn)集,非封閉曲線,具有明顯的分形結(jié)構(gòu),以上特征均表明此時(shí)系統(tǒng)處于混沌狀態(tài)。

圖9 F=0.093的Poincare截面,其他計(jì)算參數(shù)為m=1;k=0.02; c=0.04;γ=0.2;α1=0.2;β=0.3;μ1=0.05;μ2=0.05;ω=0.09Fig.9 The Poincare cross section when F=0.093, and other calculated parameters are m=1;k=0.02;c=0.04;γ=0.2; α1=0.2;β=0.3;μ1=0.05;μ2=0.05;ω=0.09

圖4表明激勵(lì)頻率變化引起系統(tǒng)倍周期分岔,并呈現(xiàn)不同頻率下倍周期分岔的變化的趨勢(shì)。圖5與圖6取不同頻率利用Poincare截面展現(xiàn)倍周期分岔,驗(yàn)證圖4分岔的正確性。

圖7顯示外激勵(lì)幅值變化引起系統(tǒng)倍周期分岔,并展現(xiàn)出不同幅值下倍周期分岔的演化方向。圖8與圖9取不同激勵(lì)幅值利用Poincare截面呈現(xiàn)倍周期分岔,驗(yàn)證圖7分岔的正確性。

5 結(jié) 論

本文研究一類含平方阻尼項(xiàng)的Mathieu-Duffing系統(tǒng)在簡(jiǎn)諧激勵(lì)下的動(dòng)力學(xué)特性。利用 Lyapunov理論分析系統(tǒng)的幅頻特性,由于系統(tǒng)同時(shí)受到強(qiáng)迫激勵(lì)和參數(shù)激勵(lì)的聯(lián)合作用,導(dǎo)致系統(tǒng)至多存在3個(gè)周期解支,其中1支為穩(wěn)定解、2支為不穩(wěn)定解。激勵(lì)頻率和激勵(lì)幅值的變化均可導(dǎo)致系統(tǒng)經(jīng)倍周期分岔進(jìn)入混沌運(yùn)動(dòng),且激勵(lì)幅值越大、激勵(lì)頻率越小越容易發(fā)生混沌運(yùn)動(dòng)。平方項(xiàng)阻尼項(xiàng)的存在對(duì)系統(tǒng)振動(dòng)有抑制作用,取值愈大對(duì)系統(tǒng)振動(dòng)抑制愈強(qiáng)。因此,適當(dāng)降低激勵(lì)幅值、增大激勵(lì)頻率有利于抑制混沌運(yùn)動(dòng)的發(fā)生。