小凈距隧道先行洞爆破開挖對后行洞圍巖穩定性影響研究

李旭哲, 李文杰, 畢志剛, 梁 斌

(1.河南科技大學 土木建筑學院,河南 洛陽 471000; 2.中鐵十五局集團第一工程有限公司,西安 710018)

隨著我國交通系統的發展,小凈距隧道的應用越來越廣泛。由于小凈距隧道左右洞之間距離較小,先行洞爆破施工時若產生較大的振動響應,易對中夾巖柱及后行洞圍巖穩定性造成不利影響[1-2],因此開展隧道爆破開挖過程中振動響應分析具有十分重要的意義。

近年來,諸多學者針對小凈距隧道爆破振動響應問題進行了大量研究,并取得了一定的成果。Shi等[3]采用量綱分析法研究了深埋小凈距隧道爆破振動衰減規律,建立了考慮抵抗線和臨空面的薩多夫斯基擴展公式。蒙國往等[4]以福州地鐵2號線某區段小凈距隧道為工程背景,對循環爆破荷載作用下圍巖的累積損傷演化過程進行了研究,發現圍巖損傷范圍和損傷程度與爆破加載次數成線性增加關系。于麗等[5]將圍巖等級、炸藥量、凈距和交叉角度作為影響因素,對超小凈距交叉隧道爆破施工進行了研究分析,依據其結果提出了超小凈距交叉隧道爆破的控制標準。劉閩龍等[6]以濟南順河快速路南延工程淺埋暗挖段施工為背景,通過軟件LS-DYNA對炮孔周圍的損傷范圍進行了分析研究,并基于聲波測試原理,對施工現場小凈距隧道圍巖的損傷進行了探測。梁琨等[7]以濟南市順河快速路南延工程為背景,結合數值模擬結果和現場監測數據,針對小凈距隧道爆破開挖過程中先行洞在后行洞上臺階爆破作用下的動力響應進行了研究。劉傳陽等[8]根據爆破施工現場振動監測數據,研究了隧道分岔段控制爆破振動對相鄰隧道的影響,對相鄰隧道和后方中隔巖墻在掏槽爆破和預留光爆層爆破條件下的振動影響進行了論證。曹峰等[9]依托六月田分岔隧道為工程背景,采用LS-DYNA有限元軟件建立數值模型,分析了循環爆破荷載作用下對小凈距隧道中夾巖的影響,并根據損傷區質點振速衰減規律,通過數據擬合,建立一系列爆破變量之間的函數關系。以上學者的研究對小凈距隧道實現順利爆破施工起到了重要作用,然而目前針對先行洞隧道爆破開挖時后行洞隧道圍巖的振動速度及應力變化規律研究還較少,有待進一步探索研究。

本文結合浙江義東高速防軍小凈距隧道工程實際,通過理論分析推導出爆破振動速度與爆心距的關系,運用有限元軟件MIDAS GTS NX建立不同凈距條件隧道爆破開挖模型,將振速數值模擬結果與理論計算結果進行分析對比,驗證理論推導公式的合理性。基于圍巖振速及應力兩者之間函數關系,提出本隧道爆破控制振速閾值,為本工程及后續類似小凈距隧道工程爆破安全施工提供參考。

1 小凈距隧道爆破數值模型建立

1.1 工程概況

義東高速防軍隧道工程為六車道分離式山嶺隧道,左線起于ZK29+047,終于ZK29+557,全長510 m,縱面線形為人字坡,右線起于K29+053,終于K29+562,全長509 m,縱面線形為人字坡。進洞口段位于丘陵斜坡區,地勢起伏較大,洞口自然坡度約30°,附近圍巖呈松散～碎裂結構,水文地質條件較簡單,綜合判斷進洞口段分布Ⅳ～Ⅴ級圍巖。出洞口段位于丘陵斜坡,斜坡自然坡度約20°,表部殘破積厚約1.0～2.0 m,其余情況與進洞口類似。隧道洞身段圍巖主要為凝灰質砂礫巖夾凝灰質粉砂巖,巖質較軟～較堅硬,節理裂隙不發育～較發育,巖石完整性一般～較好,圍巖穩定性一般～較好,隧道圍巖多為Ⅲ～Ⅳ級。隧道采用鉆爆法爆破施工,掏槽采用復式楔形掏槽爆破技術。圖1為防軍隧道洞口斷面設計圖。

圖1 隧道洞口斷面設計圖Fig.1 Section design of the tunnel entrance

1.2 數值模型

以防軍隧道工程為背景,結合工程實際,利用有限元軟件MIDAS GTS NX建立三維數值模型,模擬分析時將左洞定義為先行洞,右洞為后行洞,開挖方法采用上下臺階。袁松等[10]認為爆破動力分析時,隧道模型邊界大小應取大于等于8倍洞徑大小,本文為了合理縮短模型分析時間,保證計算精度,模型X、Y、Z方向大小分別取150 m×150 m×50 m。模型分析時采用單一巖體,通過室內試驗得到材料的具體參數取值如表1所示。為分析先行洞爆破開挖對后行洞圍巖的影響,建立0.1D、0.5D、D和2D(D為隧道凈距14.5 m)隧道凈距開挖模型,對圍巖的振動速度及應力進行分析研究,數值模型共有20 763個節點,72 707個單元,隧道數值模型如圖2所示。

表1 數值模擬材料參數Tab.1 Numerical simulation of material parameters

圖2 數值計算模型Fig.2 Numerical calculation model

1.3 爆破荷載參數

本文主要研究爆破荷載作用下圍巖損傷情況,不考慮其他因素影響,因此將爆破荷載視為均勻地施加在隧道襯砌上,方向垂直作用于洞壁,根據波的傳播規律,將爆破荷載形式簡化為如圖3所示的三角形爆破荷載曲線[11],圖中tR荷載升壓時間,ts為總作用時間段[12]。模型定義彈性邊界條件時曲面彈簧系數由式(1)、(2)求得,所施加的阻尼計算公式如式(3)、(4)所示。

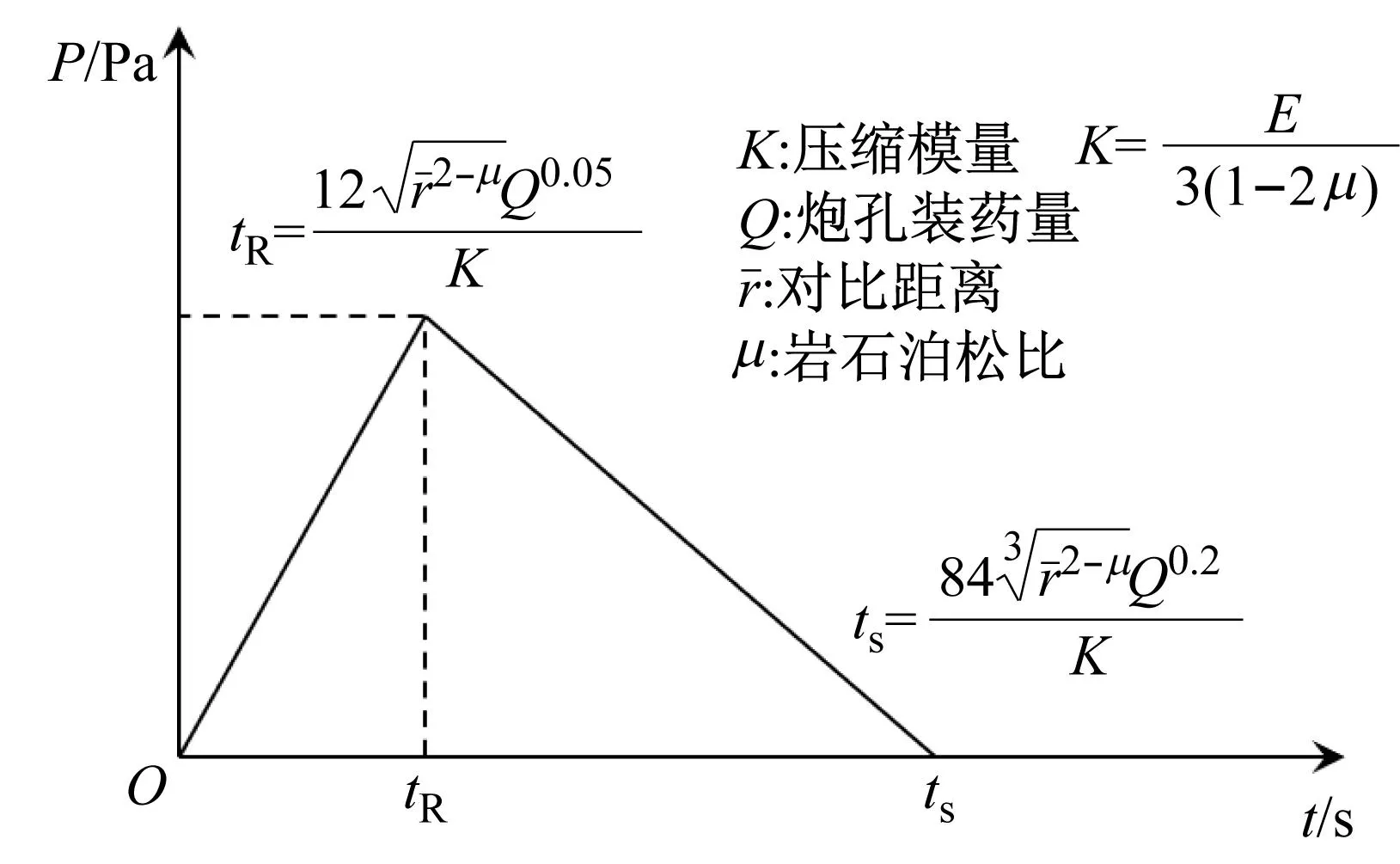
圖3 三角形爆破荷載曲線Fig.3 Triangular blast load curve

(1)

(2)

式中:kv0=1/30·α·E0=kh0,Bv=(Av)1/2,Bh=(Ah)1/2,Av和Ah分別是數值模型的豎直方向和水平方向的面積,E0是地基彈性系數,α一般取值1.0[13]。

(3)

(4)

式中:Cp為P波波速(m/s);Cs為S波波速(m/s);A為巖土單元計算面積(m2);E為彈性模量(N/m2);G為剪切模量(N/m2);γ為巖土容重(N/m3);λ為體積模量(N/m2);υ為巖土泊松比;ρ為土層密度(kg/m3)。結合表1與相關文獻,計算求得各參數取值分別為A=7 500 m2,G=1.037×107N/m2;λ=6.91×107N/m2,求得土層的阻尼常數為:Cp=359.91 kN·s/m,Cs=137.08 kN·s/m。

防軍隧道采用2號巖石乳化炸藥,根據其爆破相關參數,模型三角形荷載升壓時間取8 ms,卸壓時間為92 ms,總時間為100 ms。根據美國National Highway Institute[14]中所運用的式(5)計算爆破荷載峰值大小。式中:db為炮孔直徑大小,取db=42 mm;dc為藥筒直徑,取dc=32 m;Pdet為每kg炸藥的爆炸壓力(Pa);PB為作用于孔壁的爆破壓力(Pa);sge為炸藥比重(kg/m3);v為炸藥爆速(m/s);工程實際臺階法施工時預計每段最大用藥量44.4 kg,炸藥比重取1.15 kg/m3,炸藥爆速取3 200 m/s,計算防軍隧道爆破時每1 kg炸藥產生的壓力PB=1.13×107Pa,開挖每段壓力大小為5.02×108Pa。

(5)

2 小凈距隧道后行洞圍巖振速理論預測分析

考慮到爆破釋放的沖擊波在傳播過程中具有一定衰減特性,當超過一定范圍后,沖擊波將轉化成具有周期的地震波。由于后行洞隧道圍巖距離先行洞爆破中心較遠,因此后行洞圍巖在先行洞隧道爆破過程中主要受地震波的影響。受各種因素影響的地震波在傳播過程中能量不斷減少,消耗的能量與傳播距離成正比,具體表達如式(6)所示[15]

E=E0e-2βr

(6)

式中:E為地震波傳播距離r時的能量;E0為初始能量;r為地震波的傳播距離;β為介質對能量的吸收系數。

地震波初始能量E0與炸藥總能量Ee之比為能量轉換系數η[16-17],其中η=10-3(k·10-2)3/a。

E0=ηEe=10-3(k·10-2)3/aEe

(7)

將式(7)代入式(6)得

E=e-2βr10-3(k·10-2)3/aEe

(8)

隧道爆破時產生的能量與圍巖振速平方成正比

(9)

結合式(7)～(9)可得振動速度與爆破距離之間的關系見式(10)

(10)

等式兩邊開平方得到式(11)

vr=10-3/2·v0(k·10-2)3/(2a)e-βr

(11)

式中:vr為爆心距r時的圍巖振速大小;v0為爆破開始時的初始速度,將其視為爆源處巖石的振動速度;k為地形、地質系數;α為衰減指數。β可通過其與振幅之間的關系式(12)擬合計算[18]。

(12)

式中,A為爆破地震波振幅。

防軍隧道項目結合場地條件及工程實際,對系數k,α分別取k=150,α=1.5。地震波吸收系數β通過施工現場爆破振速和爆心距監測數據整合處理,進行擬合分析。施工現場對隧道出洞口段鄰近水庫壩體進行了爆破振動監測,測得質點XYZ三個方向的振速大小。目前通過單方向的振速大小(peak particle velocity, PPV)難以準確描述爆破特征,故引入振速三個方向的矢量和(peak velocity summation, PVS),其表達形式見式(13),文獻[19]證明PVS可以提供更加準確的振動速度估算。

(13)

通過CAD設計圖紙測得爆破監測點與爆源之間距離,振速大小與爆心距之間關系如圖4所示。將振速矢量和PVS與爆心距兩者進行擬合分析,結果如圖5所示,擬合公式為y=726.584 5e-0.067 52x,R2=0.966 51。結合式(12)及擬合結果,防軍隧道巖層介質吸收系數β取0.034。

圖4 質點各方向振動速度隨爆心距變化曲線Fig.4 The curve of particle vibration velocity in each direction with detonation distance

圖5 振速矢量和PVS與爆心距擬合分析Fig.5 The fitting analysis of the vibration velocity vector PVS and detonation distance

綜合上述分析,將爆破系數k、a、β代入式(11),可得防軍隧道工程爆破施工時,地震波在巖石介質傳播過程中振速與爆心距之間的關系式為

vr=10-3/2·v0(150·10-2)e-0.034r=

0.047v0e-0.034r

(14)

通過式(14)可對后行洞隧道圍巖振速進行預測分析。防軍隧道爆破施工時,由于受到施工條件的限制,因此無法通過現場監測獲得后行洞隧道預貫通段圍巖的應力重分布和破壞形態。為此,根據所建立的數值模型,設置不同工況,對先行洞隧道爆破過程中后行洞隧道圍巖振速大小、應力分布情況進行深入分析。

3 數值模擬計算與分析

模型模擬時,采用與工程相同的上下臺階法,選取不同凈距條件下相同隧道斷面進行分析,左右洞掌子面處于同一平面內。沿隧道開挖輪廓線共布置8個監測點,具體布局如圖6所示。其中1～5號監測點位于迎爆側面,6～8號監測點位于背爆側面。

圖6 隧道圍巖監測點布置圖Fig.6 Layout of the tunnel surrounding rock monitoring points

3.1 振動速度分析

圖7為不同凈距條件下后行洞圍巖監測點振速峰值雷達圖。

圖7 不同凈距條件監測點振速雷達圖Fig.7 Radar chart of vibration velocity at monitoring points with different clear distance conditions

由圖7可知,圍巖最大振速始終出現在3號監測點,即拱腰處,拱腰與拱腳兩者大小較為接近,圍巖振速大小從拱腰→拱腳→拱肩→拱頂(底)逐漸減小,施工時應對隧道拱腰及拱腳處加強監測。隨著隧道凈距逐漸增大,同一監測點的振速峰值隨之減小。

圖8(a)、(b)分別為后行洞上臺階與下臺階開挖后圍巖監測點振速對比圖。

(a) 上臺階開挖

(b) 下臺階開挖圖8 不同凈距條件監測點振速峰值對比圖Fig.8 Comparison of the peak vibration velocity of monitoring points with different clear distance conditions

根據GB 6722—2014 《爆破安全規程》[20]規定交通隧道的質點安全振動速度控制標準為10～20 cm/s,考慮到防軍隧道出口鄰近水庫壩體,為此本文隧道振速安全控制閾值取10 cm/s。由圖7可知,在相同凈距條件下,迎爆側監測點振速遠大于背爆側,后者約為前者的0.5倍～0.8倍,且背爆側監測點振速總體變化趨勢較小。由于左右隧道之間圍巖的存在消耗了部分爆破產生的能量,故隨著隧道凈距的增大,同一監測點的振速越小,總體變化曲線逐漸朝直線發展。當隧道凈距為0.1D時,后行洞隧道圍巖的八個測點最小振速達到了12.47 cm/s,超過了控制標準,此時先行洞隧道爆破振動易對后行洞隧道圍巖穩定性造成影響,文獻[21]將圍巖質點振速大小作為隧道爆破后圍巖損傷判據,在最不利工況0.1D凈距條件下,下臺階開挖后圍巖最大振速峰值為206.4 cm/s,文獻[22]中的Bauer和Calder判據認為當振速峰值大于63.5 cm/s小于254 cm/s時,圍巖會產生嚴重的拉伸裂縫及一些徑向裂縫,因此后行洞預貫通段應提前采取相應措施,防治爆破對隧道穩定性造成不利影響。當隧道凈距大于2D時監測點振速均滿足規范要求,結合項目實際情況,將隧道凈距2D作為安全凈距的分界線。在相同凈距條件下,開挖下臺階時隧道同一位置的振動速度大于上臺階,隧道凈距越小,兩者的振速差值越大。在安全凈距2D條件下,上臺階開挖最大振速峰值為8.23 cm/s,下臺階為9.87 cm/s,后者約是前者的1.2倍。

3.2 應力分析

圖9～12為不同凈距條件下先行洞開挖圍巖最大主應力σ1(kN·m2)變化云圖。

(a) 上臺階

(b) 下臺階圖9 凈距0.1D條件下圍巖應力分布Fig.9 Stress distribution of surrounding rock with a net distance of 0.1D

(a) 上臺階

(b) 下臺階圖10 凈距0.5D條件下圍巖應力分布Fig.10 Stress distribution of surrounding rock with a net distance of 0.5D

(a) 上臺階

(b) 下臺階圖11 凈距D條件下圍巖應力分布Fig.11 Stress distribution of surrounding rock with a net distance of D

(b) 下臺階圖12 凈距2D條件下圍巖應力分布Fig.12 Stress distribution of surrounding rock with a net distance of 2D

通過圖9～12發現,先行洞隧道爆破時,應力變化主要集中在先行洞隧道圍巖周圍,應力影響范圍隨著隧道凈距的增加而擴大,左右隧道間中隔巖壁的應力大小隨著凈距的增加而逐漸減小,凈距為2D時,提取左右洞間某點,發現其應力大小達到了約0.71 MPa,且后行洞隧道圍巖及中隔巖壁的應力值均小于其抗拉強度,表明此時先行洞爆破對其穩定性造成的影響幾乎忽略不計,隧道整體處于安全穩定狀態。上臺階開挖后,先行洞隧道圍巖的最大應力主要分布在下臺階頂部附近,下臺階開挖后,圍巖最大應力主要分布在掌子面拱底與拱腰附近,應力分布范圍較大,下臺階開挖后的影響范圍遠大于上臺階,凈距為0.1D條件下,上臺階開挖后圍巖最大主應力為4.26 MPa,下臺階開挖后為6.13 MPa,最大主應力大于巖石抗拉強度時,會導致隧道局部圍巖開裂,嚴重時造成圍巖坍塌。隨著凈距的增大,圍巖應力總體呈減小趨勢,先行洞隧道爆破開挖對后行洞隧道圍巖的影響逐漸減小,最終趨于穩定狀態。

3.3 振速計算理論驗證

為了驗證振速理論預測公式(14)的合理性,取隧道凈距D時振速數值模擬結果與理論計算值進行對比分析。隧道凈距為D時左右洞掌子面平行距離為14.5 m,縱向以10 m為一間隔,即爆心距r的取值分別為17.6 m、24.7 m、33.3 m、42.5 m、52 m,將數值模擬中爆源處圍巖的振動速度作為v0,其值為1.6 m/s。理論計算值與模擬值對比結果如圖13所示。由圖13可知,爆破施工過程中振速理論計算結果與模擬結果相對誤差較小,最大相對誤差為5.7%,通過數值模擬方法的驗證,說明本文基于理論推導的振動速度預測公式具有一定合理性。

圖13 凈距D條件下圍巖理論計算值與模擬值對比Fig.13 Comparison of theoretical and simulated values of surrounding rock with a clear distance D

4 隧道振動安全標準及工程實例

4.1 振速安全標準

目前,工程實踐上對隧道振動速度控制閾值的設定主要依賴于規范要求及施工經驗,對振速如何合理取值方面還鮮有研究。先行洞爆破開挖時,后行洞圍巖在不同凈距條件下的應力峰值和振速峰值變化情況如圖14所示。由圖14可知,圍巖左拱腰及拱腳的振動速度最大,為圍巖振動響應的危險處,整體來看,圍巖最大應力及振速皆隨著凈距的增大而減小,從統計學角度出發確立圍巖應力峰值與振速峰值兩者間函數關系。

(a) 振速峰值(cm/s)

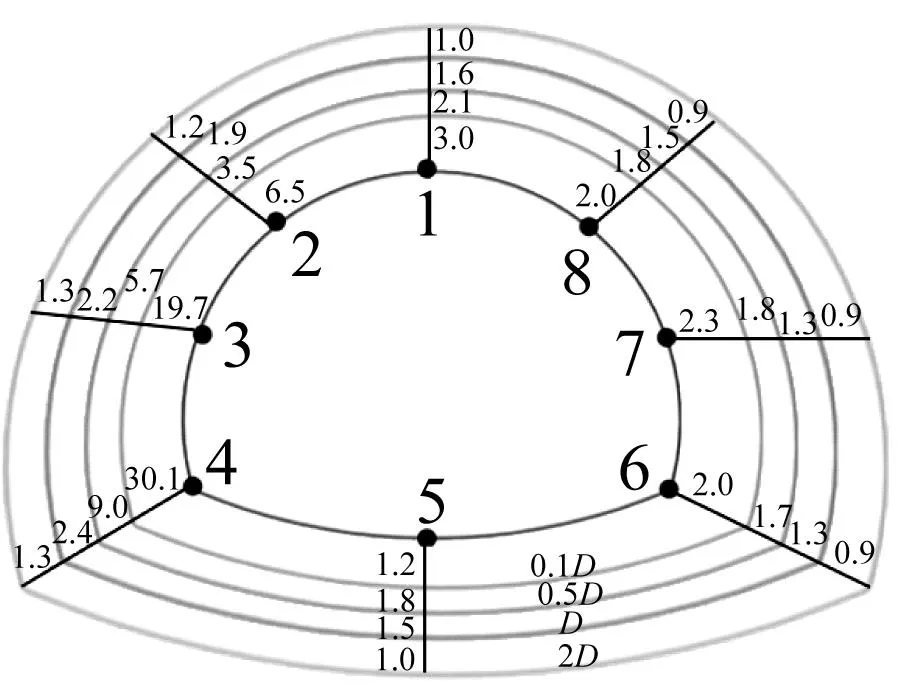
(b) 應力峰值(MPa)圖14 圍巖在不同凈距條件下應力及振速峰值Fig.14 Peak stress and vibration velocity of surrounding rock under different clear distance conditions

圖15為隧道振速峰值與應力峰值的統計關系,兩者之間的關系表達式為

圖15 圍巖振速大小與應力大小的統計關系Fig.15 Peak velocity and stress fitting analysis of the surrounding rock

σ=-0.969 02+0.282 2v

(15)

式中:σ為應力大小,MPa;v為振速大小,cm/s。在式(15)中,R2=0.998 78,結果表明后行洞隧道應力峰值與振速峰值具有較好的線性關系。當圍巖應力小于其抗拉強度時,表明圍巖處于安全穩定狀態,依據巖石的抗拉強度可計算得到爆破作用下圍巖振動速度控制閾值。綜合考慮防軍隧道地質情況,隧道巖石抗拉強度大小取3.5 MPa,將其代入式(15),計算得到:當圍巖振動速度峰值為1.9 cm/s時,所受應力達到其抗拉強度。

4.2 工程案例

根據爆破應力波的傳播理論,既有隧道在爆破施工時,為了保證鄰近隧道的安全,須對爆破強度進行控制,進而避免對相鄰隧道造成不利影響。防軍隧道進口段為小凈距部分,左右洞掌子面之間距離較小,為了降低爆破擾動影響,防軍隧道施工現場根據爆破斷面的位置,對爆破震動的影響范圍進行初步估計,在其影響范圍內的隧道斷面上布設L20-N爆破測振儀對圍巖振速進行監測。

防軍隧道施工現場振動監測如圖16所示。進口段圍巖振速監測數據如表2所示。通過表2可以得到,隧道樁號K29+075、095、115三者PVS理論大小與現場監測相對誤差分別為7%,2.66%,2.58%,結果表明理論研究結果能夠較好的應用于實際工程,通過理論計算從而避免爆破施工對圍巖穩定性造成不利影響。

圖16 施工現場爆破振動監測Fig.16 Construction site blasting vibration monitoring

表2 隧道進口段振速監測數據Tab.2 Vibration velocity monitoring data of tunnel entrance section

5 結 論

針對先行洞隧道爆破施工對后行洞圍巖穩定性影響問題,本文基于能量衰減理論,結合數值模擬手段,對后行洞隧道圍巖振速及應力變化規律進行了研究。主要結論如下:

(1) 圍巖振速理論計算值與模擬值最大相對誤差為5.7%,與現場監測數據最大相對誤差為7%,表明該理論能較好地應用于相應隧道,對隧道爆破安全施工研究具有一定的工程應用價值。

(2) 振速峰值與隧道爆破中心距呈負相關,爆心距越大,對圍巖擾動越小。根據振速分析結果,將凈距2D定義為最小安全凈距,左右洞隧道間距小于2D時,應加強對后行洞隧道圍巖的監測。

(3) 隧道后行洞圍巖迎爆側監測點振動速度大于背爆側,其結果從拱腰→拱腳→拱肩→拱頂(底)逐漸減小,相同凈距條件下,同一監測點下臺階爆破時振速峰值大于上臺階。隨著凈距增大,先行洞爆破對后行洞圍巖的擾動逐漸減弱,最終忽略不計。

(4) 不同凈距爆破開挖作用下,后行洞隧道圍巖的應力峰值與振速峰值具有線性關系,兩者隨著凈距的增大而減小,隧道拱腰及拱腳為易發生破壞的危險點。根據巖石的抗拉強度計算得到防軍隧道爆破振動速度安全閾值為1.9 cm/s,為類似工程提供了確定控制振速閾值的方法。