無速度傳感器的異步電動機模糊自適應PI直接轉矩控制*

溫瀚斌 崔彥良

（蘭州交通大學機電工程學院，甘肅 蘭州 730070）

在異步電機多種控制策略中，應用最廣泛的兩種控制策略是矢量控制和直接轉矩控制。矢量控制通過控制轉矩和磁鏈滯環來實現電機轉矩和磁鏈的直接控制，現如今，矢量控制策略的實現常與西門子、羅克韋爾變頻器結合，但電機參數變化對電機的動靜態性能影響較大，難以達到控制要求。文獻[1]采用矢量控制方法控制車輛異步電機，控制效果良好。直接轉矩控制則是通過控制電機定子電流的α-β軸分量來控制電機的轉矩和磁鏈。直接轉矩控制的動態性能優于矢量控制，并且控制精度高，控制方法簡單。

對于無速度傳感器理論，模型參考自適應系統（model reference adaptive system，MRAS）的應用更為廣泛，由于結構簡單、算法簡潔、與數字控制系統相結合實現相對容易，并且已有文獻證明MRAS 系統穩定收斂。文獻[2]設計了一種帶有負載擾動補償的改進型MRAS 觀測器，具有好的魯棒性和動態性能。對于異步電機，文獻[3]設計了一種關于定子磁鏈的滑模MRAS 觀測方法，更適用于直接轉矩控制，同時進行仿真驗證證明其具有更快的響應速度和良好的動靜態性能。文獻[4]設計了一種新型MRAS 的PMSM 無差拍電流預測控制，提高了其魯棒性。文獻[5]將MRAS 方法加入12 扇區直接轉矩控制反步控制法中，獲得了良好的控制性能。

以往，PID 控制算法常被用于電機控制領域，其在中低速范圍內控制精度較高，但動態調速性能及穩定性較差，轉矩脈動大。為了克服以上缺點，需與其他控制方法相結合。近些年來，眾多研究人員將模糊控制應用到直接轉矩控制系統中。文獻[6-7]中，研究者將模糊控制應用到永磁同步電機的矢量控制中，以此達到更好的調速性能。文獻[8]針對永磁同步電機直接轉矩控制中的轉速環、轉矩環和磁鏈環，提出了一種模糊控制器，實時調節PID 參數的方法，獲得了良好的調速性能。

模糊直接轉矩系統轉速誤差e和誤差變化率ec會隨著系統持續運行而減小，然而上述研究都忽略了這一特性，從而使得Fuzzy 規則并未被充分利用，導致系統運行速度變慢，調速性能變差。針對此問題，部分研究者引入伸縮因子概念，將變論域Fuzzy PID 應用于電機控制。文獻[9]將其引入PMSM 的矢量控制中，并加入樽海鞘群智能算法，通過仿真證明該策略在工程上具有較好的實用性和控制性能。

基于MRAS 的無速度傳感器理論對參數具有一定的依賴性，而其中的PI 增益參數通常由試湊法取得，缺乏協調控制的思想。針對此問題，本文將自耦PI 概念引入MRAS，通過引入速度因子Zc統一整定PI 參數，降低了選取不同PI 參數的不確定性。同時為了改善調速性能，將轉速環的模糊PI 控制策略改進為變論域模糊PI 控制，提升了電機無速度傳感器轉速的響應速度，提高了電機調速精度。

同時，本文將模糊PI 控制應用于轉速環當中，大大減小了轉矩脈動，提升了控制性能。同時，針對模糊規則利用率低的問題，將模糊PI 控制改進為變論域模糊PI 控制，提高系統的響應速度和魯棒性，減小轉矩脈動。

基于此，結合實際工程應用背景，針對上述所提研究策略搭建模型并進行仿真分析，仿真結果驗證了上述方法的可行性。

1 直接轉矩控制系統

1.1 兩相靜止坐標系下DTC 數學模型

異步電機在調速時需要電壓、電流和頻率的協調控制，而輸出變量有轉速、磁通等獨立變量，這些變量之間又相互影響，是一個強耦合的多變量系統。再加上磁飽和因素、電磁慣性和機械慣性對異步電機系統的影響，造成其模型具有多階非線性的特點，在建立異步電機數學模型（圖1）時，需做以下假設：

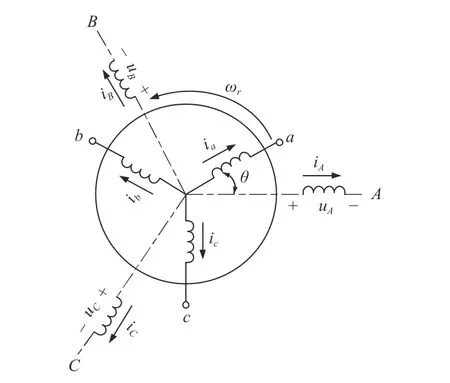
圖1 三相異步電機數學模型

（1）繞組相互間以120°均勻分布，忽略諧波影響。

（2）不考慮頻率和溫度的影響。

（3）不計鐵芯損耗。

（4）自感互感恒定，不考慮磁路飽和。

為了優化系統的控制性能，需要在不同坐標系下對電機模型進行分析，α-β兩相靜止坐標系下的異步電機數學模型如下。

（1）電壓方程

式中：下標為α表示兩相坐標系下α軸的物理量分量；下標為β表示兩相坐標系下β軸的物理量分量；下標為s表示定子側的物理量；下標為r表示轉子側的物理量；usα、usβ分別表示靜止坐標系下兩相定子電壓；isα、isβ分別表示兩相定子電流；urα、urβ分別表示兩相轉子電壓；irα、irβ分別表示兩相轉子電流；Rs為定子電阻；Rr為轉子電阻；Ls、Lr、Lm分別表示定子電感、轉子電感和定轉子互感。

（2）磁鏈方程

式中：ψsα、ψsβ表示兩相定子磁鏈；ψrα、ψrβ表示兩相轉子磁鏈。

（3）轉矩平衡方程

式中：Te表示電磁轉矩；TL表示負載轉矩；J表示轉動慣量；np表示磁極對數；ωr表示轉子轉速。

1.2 直接轉矩控制系統結構

直接轉矩控制系統的基本組成包括電壓型逆變器、電流和電壓變換器、磁鏈和轉矩計算模塊、磁鏈和轉矩調節模塊以及開關信號選擇單元。首先測出逆變器輸出的定子電壓和定子電流，經過坐標變換轉換成α-β坐標系下的定子電壓和定子電流，再利用磁鏈計算模塊算出磁鏈矢量的投影，轉矩計算模塊算出轉矩值，將磁鏈矢量投影進入磁鏈自控制單元進行定子磁鏈區段判斷，得出開關信號，轉矩值經轉矩調節單元后，得到轉矩控制信號來控制轉矩大小的調控，開關信號和轉矩控制信號共同控制逆變器橋臂的導通，使定子磁鏈軌跡沿圓形運動。

直接轉矩控制等效結構圖如圖2 所示。

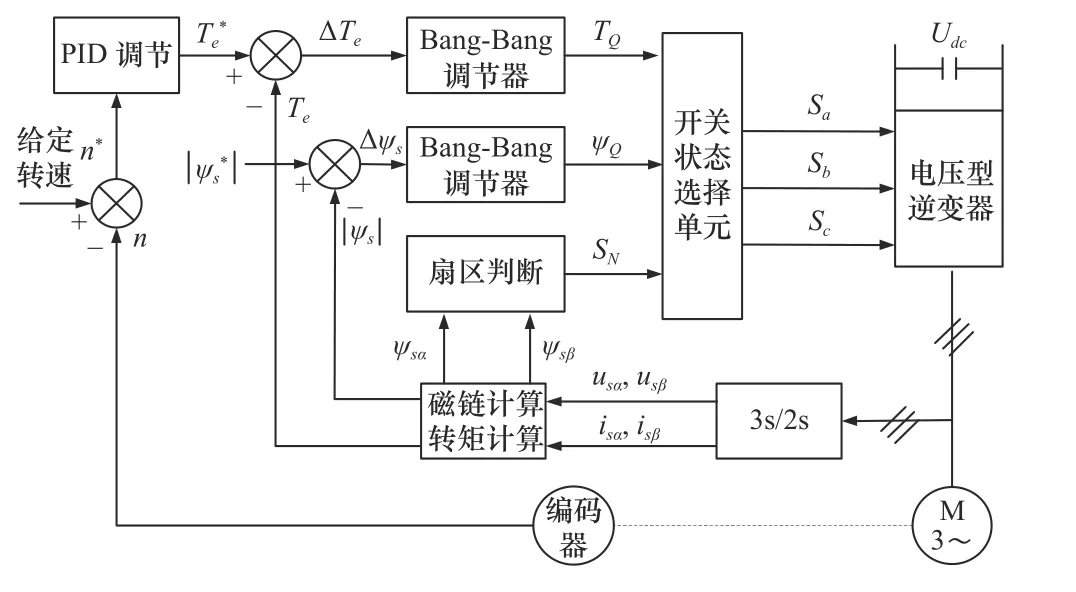
圖2 直接轉矩控制等效結構圖

2 自耦PI 無速度傳感器

2.1 MRAS 無速度傳感器

對于電機實際應用中，反饋信息的精確性影響著控制效果。若使用的編碼器或機械速度傳感器時，則該信息的可靠性降低，從而影響控制效果。基于此引入了無傳感器控制技術來基于機器模型估計速度。然而，對于直接轉矩控制系統來說，很難找到合適的定子磁鏈估計和速度估計方法，因此本文采用轉子磁鏈參考模型和可調模型。基于參考模型和可調模型之間的比較來估計系統變量。獲取這兩個模型之間的誤差驅動產生估計速度的自適應機制。參考模型表示如下：

可調模型表示如下：

參考磁鏈中的磁鏈估計和可調節模型之間磁鏈估計的誤差用于控制適當的自適應機制，該自適應機制產生估計速度，磁鏈誤差表示如下：

根據Popov 超穩定性定律，可以得到觀測轉速表達式為

2.2 自耦PI 算法

對于傳統MRAS 無速度傳感器中PI 控制增益多使用試湊法，即根據經驗試湊出合適的參數。傳統PID 控制器中，KP、KI、KD三個控制參數相互獨立，缺少協調性，由此導致調節困難，文獻[10]提出自耦PID（auto-coupling PID，AC-PID）算法，通過引入速度因子Zc統一表示PID 控制器的增益參數，緊密結合PID 控制器中比例、積分、微分環節去控制信號，增強了其物理環節的協同性。這種控制算法對于后期系統的調試工作進行了極大的簡化，也改變了如今PID 控制器中參數皆為獨立的現狀，具有很高的研究價值。當期望為定值時，可以得到自耦PID 控制律[10]為

式中：e1為跟蹤 誤差；e0表示對e1積分；e2表示對e1微分；b0是通道增益的估計值，b0≠0。

在傳統MRAS 中，采用PI 控制器得到觀測轉速，省去了微分環節。結合傳統PI 的控制率可以得到自耦PI 的控制律為

自耦PI 的整定規則[11]為

式中：Zc為自適應速度因子。文獻[11]給出了ACPI最小速度因子參考模型：

式中：1 ≤α ＜10；Tr是系統過度到穩態所需要的穩態過度時間[12]。

由于ACPI 控制器沒有微分環節，無需考慮自適應速度因子，因此其速度因子可為

自耦PI 不僅遵循了量綱匹配原則和協同控制的科學思想，而且相比于傳統PI 具有更強的魯棒性。所以將自耦PI 應用到模型參考自適應上進行轉速估計。

據MRAS 轉速估計所到達的穩定時間可得，Tr約為0.15。

3 轉速環變論域靜態Fuzzy PI 控制器

3.1 Fuzzy PI 控制器

針對上述異步電機無速度傳感器轉速波動，調速性能差等特點。設計模糊自適應PI 控制器，其控制策略如圖3 所示。

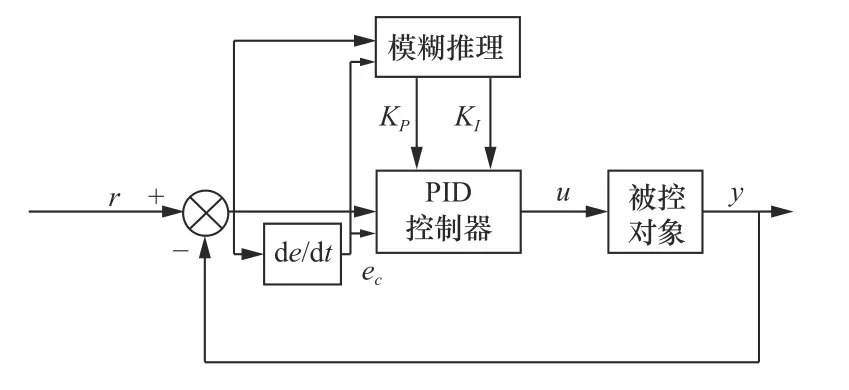
圖3 模糊控制策略圖

在轉速環由傳統的PI 控制變為帶有伸縮因子的變論域模糊PI 自適應技術自適應調節比例增益和積分增益，減小轉矩脈動。控制器輸入選擇轉速偏e和轉速偏差變化率ec，并基于此選取合適的隸屬函數，由人為經驗指導制定適當的模糊規則表，控制時據此推理，之后進行解模糊環節，將解模糊后所計算出的推理值作為整個模糊控制器的輸出增益值，運算得到更新后的KP、KI作為該環節輸出[13]。更新后的KP、KI表示為

根據傳統 Mamdani 型模糊理論作為模糊控制器。模糊控制器建立過程如下。

3.1.1 模糊化

設定標稱轉速1 500 r/min，本文選擇轉速偏差eωt和偏差變化率ecωt為模糊控制輸入，選取轉速環PI 控制增益 ΔKPω、ΔKIω為控制輸出。根據系統特性以及多次仿真經驗綜合考量，設定轉速偏差eωt和轉速偏差ecωt變化率的論域均為[-6,6]，而在轉速環PI 控制器中，為了提升響應時間的同時限制積分飽和，設定控制參數KP是KI的10 倍左右，根據多次仿真經驗可得控制增益 ΔKPω和 ΔKIω的論域分別設置為[-10,10]和[-1,1]。確定輸入量論域后需將轉速偏差和偏差變化率由數字量轉化為模糊量，通過伸縮因子將其量化到論域中，此過程則需通過選取適當的伸縮因子實現。若設真實偏差變化范圍為[-x,x]，模糊論域為[-h,h]，則量化因子[14]選擇為

其次確定論域上的模糊語言變量。在相應論域上用{NB,NM,NS,ZO,PS,PM,PB}描述輸入變量的大小程度，其對應的中文為{負大，負中，負小，零，正小，正中，正大}。隸屬度函數的選取是根據輸入變量的大致分布狀況確定的[15]，按照一般原則選取三角函數作為輸入輸出變量的隸屬度函數。隸屬度函數如圖4～圖6 所示。

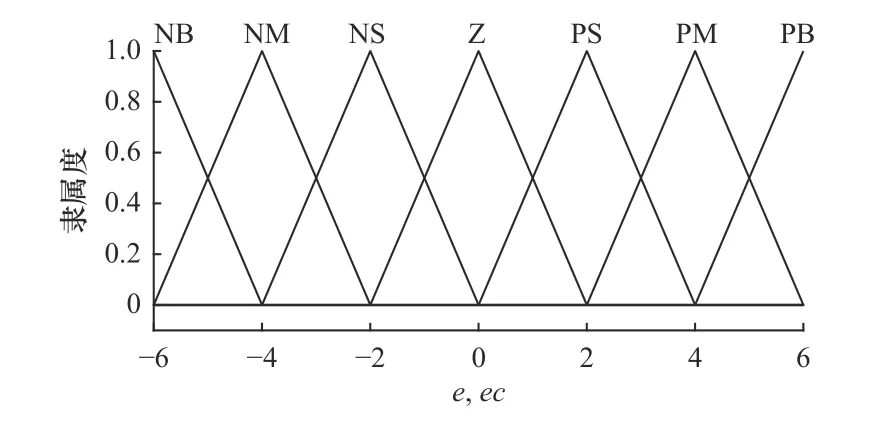
圖4 模糊輸入隸屬度函數

圖5 模糊輸出 KP隸屬度函數

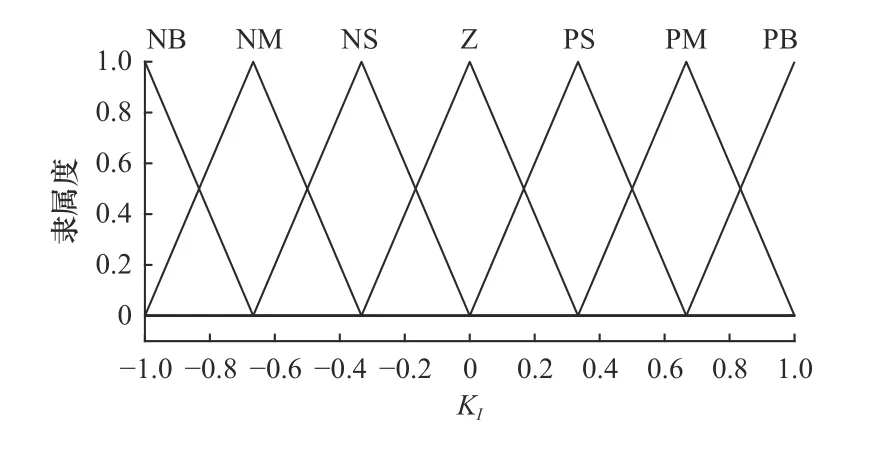
圖6 模糊輸出 KI隸屬度函數

3.1.2 模糊推理（規則庫）

模糊規則的建立很大一部分取決于人的經驗，同時控制效果的好與壞也同樣取決于模糊規則庫的建立。一般用“IF···THEN···”語句對模糊化后的輸入輸出關系進行邏輯判斷。對于異步電機來說，若轉速偏差eωt較大，則需加大比例增益變化量ΔKPω取值，以此縮短響應時間，同時需減小積分參數變化量 ΔKIω取值，以此減小超調量；若轉速偏差eωt和轉速偏差變化率ecωt的值處于居中水平，需要在維持一定的響應速度的前提下盡可能減小超調量，需減小比例參數變化量 ΔKPω的取值，ΔKIω都應取適中值；若轉速偏差eωt較小，系統靜態誤差較大，需減小 ΔKPω和 ΔKIω的取值。根據上述邏輯，轉速環ΔKPω和 ΔKIω模糊規則分別見表1 和表2。

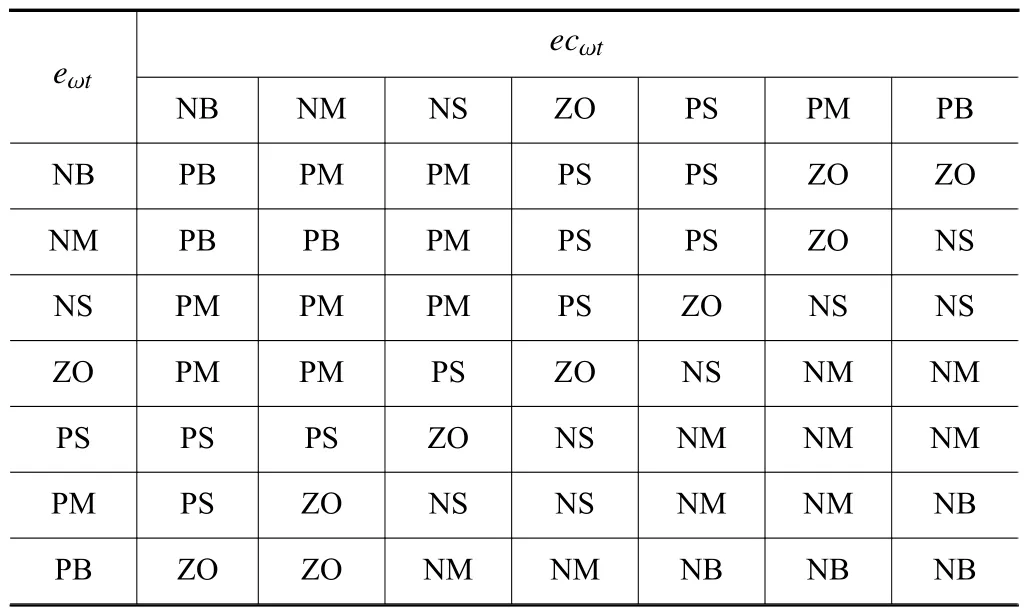
表1 ΔKPω模糊規則表

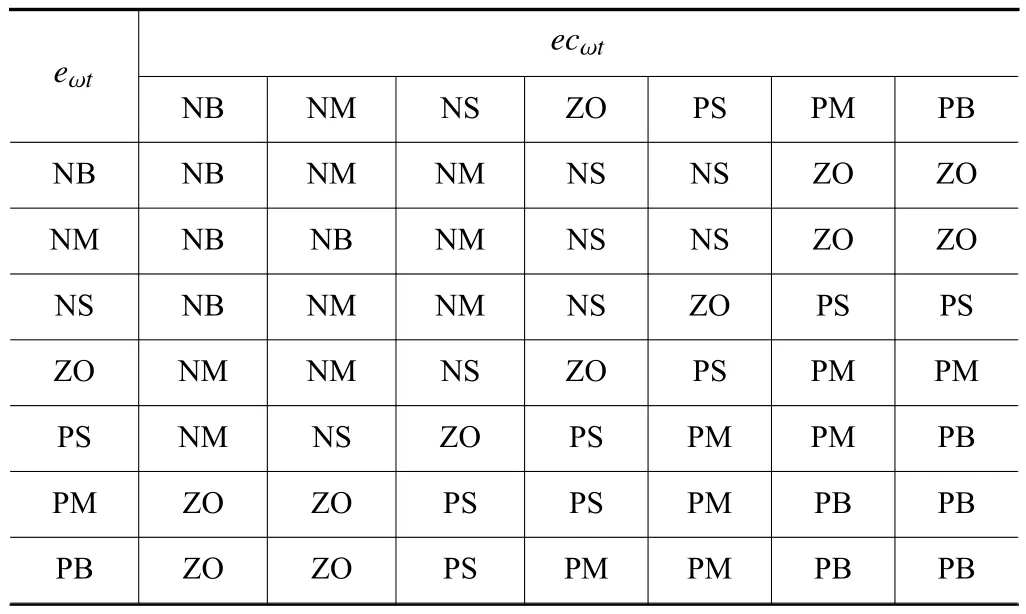
表2 ΔKIω模糊規則表

3.1.3 去模糊化

去模糊化是指將模糊推理后的輸出變量語言值通過去模糊化這一過程轉變為數字量，常用的去模糊化方法有最大隸屬度法、加權平均法等。本文采用加權平均法對輸出變量進行去模糊化。

3.2 變論域模糊PI 控制器

變論域的實質就是在已經確定隸屬度函數的條件下，將伸縮因子由原有的固定數字改變為可變的伸縮因子，從而使得初始論域能夠隨著誤差同向變化，論域的改變同樣也意味著模糊規則的使用率更高，系統性能得到優化，所以伸縮因子的設計則是至關重要的。選擇伸縮因子有幾種不同的方式：函數映射型伸縮因子、誤差分級型伸縮因子以及模糊推理型伸縮因子。本文選取函數類型論域伸縮因子構造方法，所選取的函數必須滿足5 個條件，即協調性、單調性、正規性、對偶性和避零性[16]。采用常用的函數模型作為輸入輸出變量的伸縮因子[17]：

式中：λ ∈(0,1)；k為比例常數，k＞0 ；β(0)為初值。

對于輸人變量e、ec量化因子的伸縮因子，k的取值主要取決于控制系統的靈敏性要求，k值越小，系統響應越慢。λ的取值主要取決于控制系統的精確度要求。根據經驗選取：

對于輸出變量 ΔKP、ΔKI比例因子的伸縮因子，需要綜合考慮 ΔKP、ΔKI對控制系統性能的影響。ΔKP隨誤差單調變化，ΔKI隨誤差單調反變化。根據經驗選擇伸縮因子如下：

改進后的轉速環變論域靜態模糊控制器結構如圖7 所示。

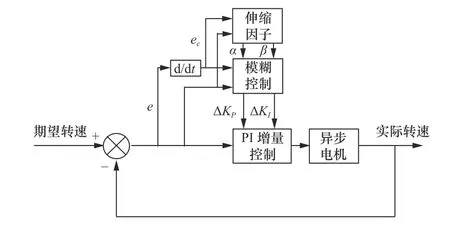
圖7 轉速環變論域模糊PI 控制器結構圖

3.3 變論域靜態模糊PI 控制器

由3.2 可知轉速環變論域模糊PI 控制器為

式中：控制增益KPω、KIω由變論域模糊控制自適應調整。由式（3）可知，當轉速 ωr達到期望值，即轉速偏差調整為零后，電磁轉矩Te隨之達到其期望值，由此可設計如下轉速環變論域靜態模糊PI 控制器：

當轉速偏差不為零時，變論域模糊PI 控制起作用，驅動轉速偏差為零，使得轉速 ωr達到期望轉速；當轉速偏差為零時，定制控制起作用，使得電磁轉矩Te達到期望值。

4 仿真驗證

為驗證所提控制方法的有效性，本文以三相異步電機作為研究對象，利用 Matlab/Simulink 建立仿真模型，對本文所提方法進行仿真驗證。

電機在負載擾動及轉速突變情況下，電機空載啟動，給定初始轉速為400 r/min，在0.35 s 施加50 N·m的負載，在0.4 s 時加速至1 500 r/min。將有感實際轉速與ACPI-MRAS 觀測轉速進行對比，得到兩種轉速觀測方法對比圖，如圖8 所示。

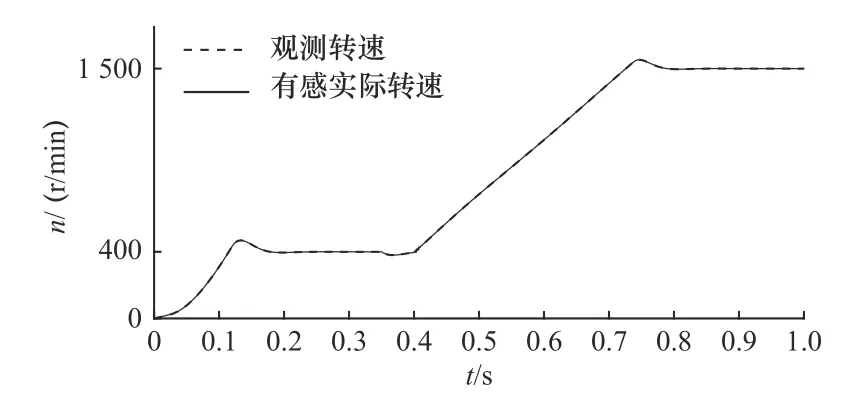
圖8 觀測方法與實際轉速對比圖

將ACPI-MRAS 觀測轉速作為轉速環輸入，再將轉速環PI 改進為變論域靜態模糊PI 控制器，得到不同控制方法下的轉速圖像對比，如圖9 和圖10所示。

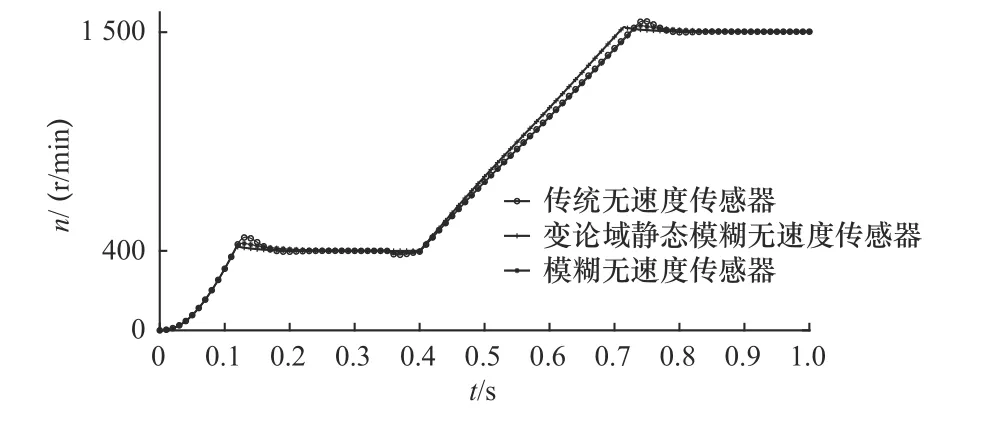
圖9 三種控制方法轉速對比

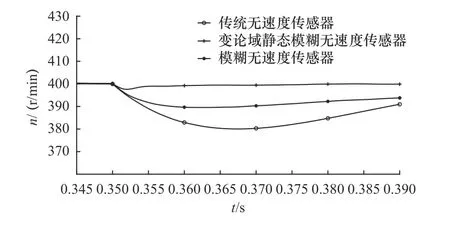
圖10 施加負載后三種控制方法抗負載能力對比

由圖9 可以看出，低速工況下傳統PI 控制下的MRAS 無速度傳感器轉速波動較大，超調量約為10%，響應時間為0.15 s；在傳統模糊PI 控制下的MRAS 無速度傳感器轉速超調量為5%，響應時間也為0.15 s；而在轉速環改進為變論域靜態模糊PI 控制后，轉速超調量為2.25%，響應時間依舊為0.15 s。高速工況下傳統PI 控制下的MRAS 無速度傳感器超調量較大，約為3.67%，在傳統模糊PI 控制下的MRAS 無速度傳感器轉速超調量為2.3%，且在0.84 s 達到穩態；而在轉速環改進為變論域靜態模糊PI 控制后，轉速超調量為1.67%，在0.78 s達到穩態。

結合圖10 可得，在0.35 s 施加50 N·m 時，傳統無速度傳感器的轉速在0.05 s 內恢復，且轉速動態降落為5%；傳統模糊PI 控制下的轉速在0.05 s內恢復，且轉速動態降落為2.5%；而變論域靜態模糊無速度傳感器轉速在0.01 s 內即可恢復速度，轉速動態降落值為0.37%。由此可見，施加負載時變論域靜態模糊PI 的MRAS 無速度傳感器直接轉矩控制方法大大提升了抗負載能力。

由圖11 可以得出，定子磁鏈在改進后沒有發生改變，在轉速變化過程中，控制良好且磁鏈波動小，一直為0.8 Wb。

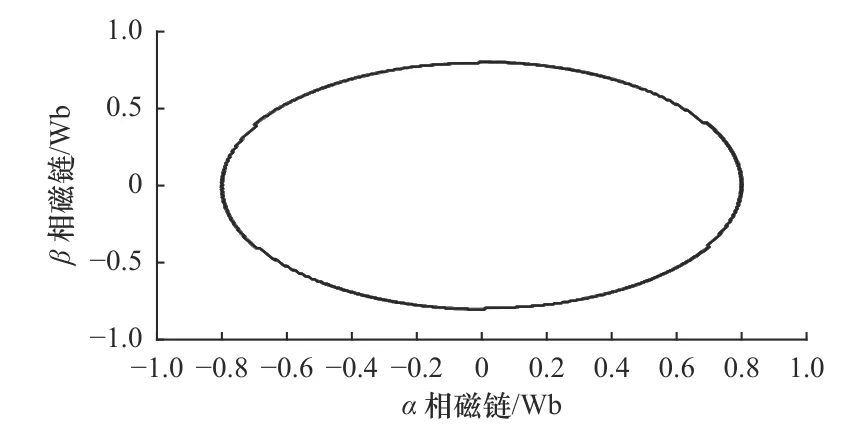
圖11 傳統觀測方法與改進后觀測兩相磁鏈圖

由圖12 和圖13 可得，高速工況下轉速環傳統PI 無速度傳感器轉矩脈動大且不平穩，在施加負載后，轉速環傳統PI 無速度傳感器轉矩波動最大值為60 N·m，波動最小值為44 N·m，差值為16 N·m；而改進為變論域靜態模糊PI 無速度傳感器后，轉矩波動最大值為55 N·m，波動最小值為47.5 N·m，差值為7.5 N·m。由此可得，相較于傳統PI 無速度傳感器轉矩，改進后方法轉矩波動減小了53.1%；且由于轉矩均值都為50 N·m，轉速環傳統PI 無速度傳感器轉矩波動轉矩標準差為11.02 N·m；而改進為變論域靜態模糊PI 無速度傳感器后，轉矩波動標準差為2.52 N·m。因此，相較于傳統PI 無速度傳感器轉矩，改進后方法轉矩脈動平穩性提升了77.1%，在轉速上升及高速工況穩定期間電磁轉矩更加平穩，轉矩脈動更小。

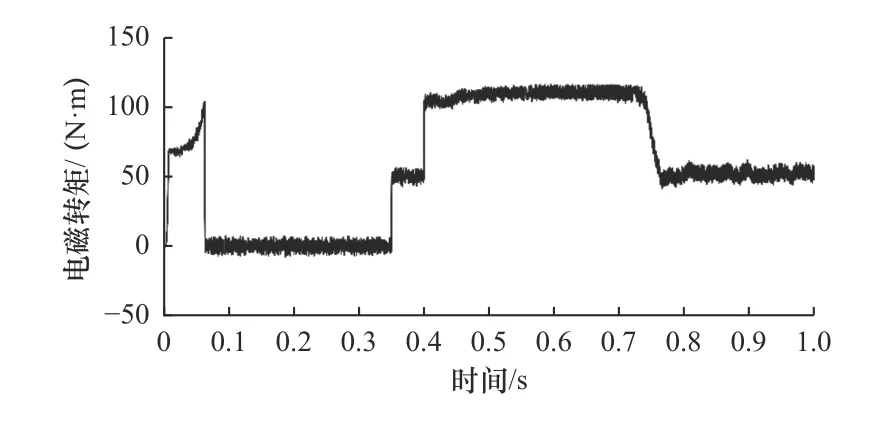
圖12 轉速環傳統PI 無速度傳感器轉矩

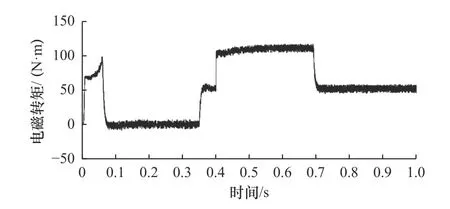
圖13 轉速環變論域靜態模糊PI 無速度傳感器轉矩

本文在轉速環加入變論域靜態模糊控制，減小了轉速超調量和縮短了響應時間，減小了轉矩脈動，仿真結果表明本文所提方法有效可行。

5 結語

本文針對無速度傳感器異步電機直接轉矩控制系統PI 控制增益不協調，調速精度較差、轉矩脈動大等特點做出兩點改進，將傳統MRAS 無速度傳感器改進為自耦PI 無速度傳感器，改善調速性能，減小超調量，進而提出變論域模糊PI 控制方法取代傳統的轉速環PI 控制，進一步改善調速性能。