單元視角下的概念同化教學

林志輝　陳柯柯

［摘 要］文章基于對學情的分析，提出了一種新穎的學習路徑，即概念同化教學。以“平行四邊形的認識”教學為例，從已知概念屬性出發(fā)，通過操作、對比、概括等方式，抽象出平行四邊形的特性，引導學生從感性認識逐漸走向理性認識，幫助學生積累學習平面圖形的經(jīng)驗，形成空間觀念。

［關鍵詞］平行四邊形；空間觀念；概念同化

［中圖分類號］ G623.5［文獻標識碼］ A［文章編號］ 1007-9068（2024）05-0070-03

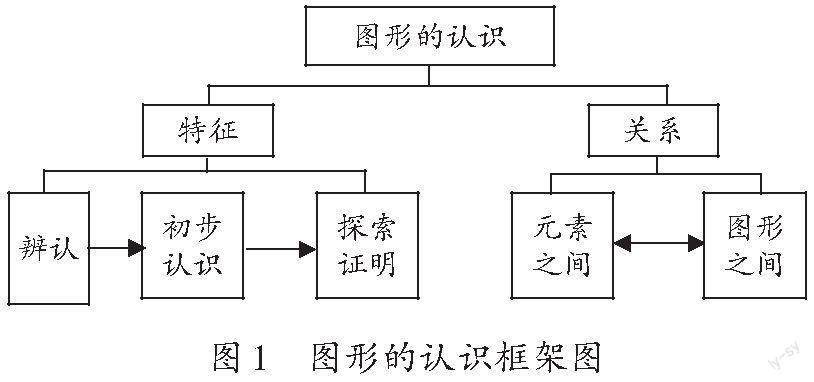
圖形的認識包括兩個方面（如圖1），一是對圖形特征的認識，經(jīng)歷從辨認到初步認識再到探索證明的不同階段；二是對圖形各元素、圖形與圖形之間的關系的認識。在教學“平行四邊形的認識”時，教什么？怎么教？筆者基于教材內(nèi)容，從真實學情和單元視角兩個方面進行了整體思考。

一、課前思考

（一）學情：從感性走向理性

學生在一年級時通過直觀感受和生活經(jīng)驗來認識平行四邊形，主要是辨認圖形的形狀。然而，在四年級學生對平行四邊形的認識中，需要用更精確的語言描述平行四邊形的特征，概括平行四邊形的定義，并辨認平行四邊形，了解其與其他平面圖形的關系。這時，學生的思維水平已經(jīng)進入抽象階段。

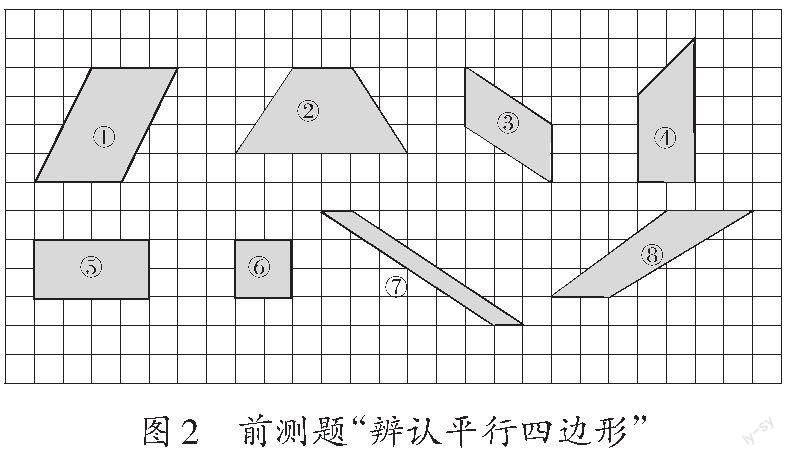
教學“平行四邊形的認識”這一課前，為了精準把握學生對平行四邊形的理解情況，筆者設計了如圖2所示的前測題。

筆者對四年級的168名學生進行了前測，從前測情況（見表1）來看，大部分學生能夠正確辨認平行四邊形，表明他們對平行四邊形有一定的認識。其中，有少部分學生選擇了⑤號圖形和⑥號圖形，而大部分學生認為長方形和正方形不是平行四邊形，這說明他們還沒有厘清平行四邊形與長方形、正方形之間的關系。此外，還有一部分學生認為⑧號圖形是平行四邊形。通過進一步了解，筆者發(fā)現(xiàn)大部分學生只關注到平行四邊形的局部特征，他們的判斷依據(jù)是整體感知和直觀感覺。

（二）需求：從合并走向獨立

平行四邊形在平面圖形板塊中具有重要的作用，與梯形有密切的聯(lián)系。對平行四邊形的編排在不同版本教材中有所變化：在1992年人教版教材和2001年人教版教材中，平行四邊形的教學內(nèi)容與梯形的合并，而2011年人教版教材將平行四邊形單獨編排為一個課時。產(chǎn)生這種變化的原因是什么呢？

筆者認為，平行四邊形和梯形的定義相似，合并教學時教學內(nèi)容較多，學生容易混淆兩種圖形，不利于辨析。而獨立教學則讓學生能夠有針對性地認識和研究一種圖形，從多個方面深入探究，有利于建構(gòu)概念。此外，獨立教學減少了教學內(nèi)容，但對學生的深度理解提出了更高的要求。

二、優(yōu)化設計

（一）材、序的選擇：從存異走向求同

人教版教材將平行四邊形的知識編排在“平行”和“垂直”之后，而其他版本教材將其編排在“認識三角形”之后。平行四邊形的定義是從線的位置關系出發(fā)的，因此，教學線的位置關系之后直接引入平行四邊形，有助于學生更好地理解平行四邊形的定義。筆者對比各版本教材后發(fā)現(xiàn)，大多數(shù)教材選擇從生活中的實例抽象出平行四邊形，以激活學生已經(jīng)積累的有關平行四邊形的感性認識。例如，浙教版和滬教版教材從數(shù)學本位出發(fā)，引導學生思考“在一組平行線上畫另一組平行線會得到什么圖形”，學生可以得出“平行四邊形的兩組對邊分別平行”的結(jié)論。從線的位置關系出發(fā)來定義圖形，有助于學生更好地理解定義。在探究部分，人教版教材提供了不同的平行四邊形，鼓勵學生自主探究圖形的特征，進而歸納平行四邊形的定義。蘇教版教材通過在格子圖中畫平行四邊形的活動，引導學生發(fā)現(xiàn)平行四邊形的特征，并由此概括出平行四邊形的定義。北師大版教材則通過圖形的分類方法得出平行四邊形的定義。這些教材的共同點是需要學生通過操作來進一步感知圖形之間的關系，并且大部分教材對于圖形的理解都有具體的要求。

（二）創(chuàng)新性路徑：從同化走向本質(zhì)

對學情進行分析、對單元內(nèi)容進行解讀后，筆者設計了關于平行四邊形的教學架構(gòu)，以引導學生建構(gòu)平行四邊形的概念，感悟平行四邊形的特征。比如，環(huán)節(jié)一，激活學生的原有認知，抽象平行四邊形的概念；環(huán)節(jié)二，學生對比課前所畫的平行四邊形，將平行四邊形和長方形、正方形關聯(lián)起來，從而理解平行四邊形的特征；環(huán)節(jié)三，學生靈活運用平行四邊形的特征畫平行四邊形，指定畫高，進一步加深對平行四邊形的理解；環(huán)節(jié)四，打破知識之間的屏障，使學生感悟知識方法的相通性。具體內(nèi)容見表2。

三、教學實踐

【片段1】

師：一個點向右移動會形成什么？向兩邊無限延伸又會形成什么？

生1：一個點向右移動會形成射線，向兩邊無限延伸會形成直線。

師：兩條直線會有怎樣的關系？

生2：在同一個平面中，兩條線會平行或相交，其中垂直是特殊的相交關系。

師：想象一下，兩組線相交會形成怎樣的四邊形？如果是兩組平行線，又會形成怎樣的四邊形？

生3：平行四邊形。

師（出示圖3）：它們長得不一樣，怎么都是平行四邊形？

生4：它們的對邊延伸的時候都不會相交，對邊都是平行的。

生5：它們的對邊所占的格子數(shù)都是一樣多的，所以對邊都是相等的。

【設計意圖】本課的導入環(huán)節(jié)有別于常規(guī)課例的“從生活實際抽象出平行四邊形”，通過點移動成線、回顧線的位置關系等方式來喚起學生的原有認知和想象經(jīng)驗。這種方式可以讓學生基于線的關系的認知，增強對“平行”的理解。通過引導學生想象兩組線所組成的四邊形，再想象兩組平行線所組成的四邊形，使學生的直觀認知和平行線的概念融合在一起。學生對平行四邊形的定義已有一定的認知，在此基礎上，運用幾何畫板的動態(tài)演示功能，能夠不斷喚醒學生的原有認知，并通過尋求共同點的方式，提煉平行四邊形的本質(zhì)特征。

【片段2】

師（出示圖4）：課前大家畫了自己想象的平行四邊形。這些圖形都是平行四邊形嗎？哪些肯定是？哪些肯定不是？為什么？

生1：想象一下，把①號圖形的兩組對邊分別向兩邊無限延伸，肯定不會相交。

生2：仔細觀察①號圖形，還發(fā)現(xiàn)兩組對邊所占的格子數(shù)分別相同。

生3：③號圖形也是這樣，所以肯定是平行四邊形。

生4：②號圖形的其中一組對邊無限延伸，肯定會相交。

生5：②號圖形兩組對邊所占的格子數(shù)都不同，而平行四邊形的對邊所占的格子數(shù)是相同的。

師：這些圖形的作者，你原來怎么想的，現(xiàn)在又怎么想？

生6：我原來認為平行四邊形就是斜著的，現(xiàn)在我知道兩組對邊必須互相平行。

生7：我認為長方形不是平行四邊形，因為它有四個直角，不是斜的。

生8：平行四邊形的特征是兩組對邊分別互相平行，長方形符合這樣的特征，因此長方形是平行四邊形。

生9：我現(xiàn)在認為生8說得對。還有，正方形應該也是平行四邊形，因為正方形也符合這樣的特征，而且它是特殊的長方形。

師：還有別的想法嗎？

生10：對于長方形、正方形，能直接看出它們的對邊是相等的。

生11：我畫的平行四邊形的兩組對邊是相等的。

【設計意圖】筆者發(fā)現(xiàn)學生對平行四邊形的直觀認知是“平行四邊形是斜的”，說明學生對矩形與平行四邊形之間的認識存在斷層。這一斷層來源于學生對圖形特征的理解不夠深入。通過對學生課前的作品進行辨析，學生進一步明確了平行四邊形的概念，豐富了對平行四邊形的理解。學生在辨析過程中從應用定義開始嘗試修正自己的作品，然后通過對邊的位置關系和長度關系學會判斷。在辨析的過程中，學生的語言表達逐步變得精準，通過不斷論述，學生將原有對平行四邊形的直觀認知轉(zhuǎn)化為對元素特征的概括，實現(xiàn)了對圖形的抽象。

綜上所述，概念教學非一日之功，從第一學段的整體感知到第二學段的特征感悟，學生需要在操作、辨析、抽象中逐步建立平行四邊形的結(jié)構(gòu)，理解平行四邊形的概念，為后續(xù)探索平行四邊形的性質(zhì)打下基礎。作為教師，應該透過整個單元，整體、全面地思考教學內(nèi)容和學生的學習情況，選擇適合自己和學生的教學路徑，引領學生進行關聯(lián)化深度學習，推動學生思維能力的成長，促進學生核心素養(yǎng)的發(fā)展。

［ 參 考 文 獻 ］

[1] 張丹.小學數(shù)學教學策略[M].北京：北京師范大學出版社，2010.

[2] 丁維虎.圖形的認識重在發(fā)展空間觀念和幾何直觀：“平行四邊形的認識”磨課歷程與思考[J].小學數(shù)學教育，2023（12）：30-33.