鐵路工程長距離帶狀GNSS控制網高精度解算

嚴 冬，李劍鋒，2，梅 熙，馮 威，黃丁發

(1.西南交通大學地球科學與環境工程學院衛星導航研究中心,成都 610097; 2.成都信息工程大學資源環境學院,成都 610225; 3.中鐵二院工程集團有限責任公司,成都 610031)

引言

鐵路工程的建設和運營都離不開高精度工程控制網的保障,而鐵路工程控制網又具有跨度大、帶狀異形、地形復雜等特點,給高精度GNSS控制測量的解算帶來挑戰[1-2]。針對鐵路工程中長距離帶狀控制網的特點,通過分析影響高精度GNSS控制測量的因子,提出優化控制網解算策略,從而改善和提高鐵路工程控制網的解算質量和性能。

鐵路工程帶狀控制網通常由短基線和中長基線混合組成。現有研究結果表明,多系統解算控制網可以得到高精度結果[3-4],于龍昊[4]和張雙成等[5-6]利用GAMIT分析了不同基線解對短基線、中長基線和消除電離層折射的影響;高旺等[6]分析了快速星歷、超快速星歷和精密星歷對基線解算精度的影響;李建濤等[7]測試了不同對流層延遲參數和不同測站約束值對基線解算的影響。衛星截止高度角會影響GNSS的定位精度,李建濤[8]和王曉明等[9-10]分析不同截止高度角對基線解算的影響情況,得到截止高度角在10°時最有利于基線解算,而隨著衛星截止高度角變大,基線解算精度逐漸變低。但以上影響分析均未針對帶狀控制網的特點展開討論。對于鐵路工程控制網,陶燦等[11]發現單GPS星座和單BDS星座處理帶狀控制網時精度相當;匡團結[12]分析了不同基線解類型對帶狀控制網的解算效果;周東衛[13]對高鐵控制網使用不同星歷產品和對流層延遲參數做了評估。在以上研究中,大多只對1～2項解算參數進行分析,少有針對帶狀控制網的高精度解算形成一套系統的解算策略。

因此,本文針對影響帶狀控制網解算的多個因子,采用不同的解算策略進行基線解算實驗,利用質量指標篩選出長距離帶狀控制網優化解算策略,并結合復雜地形環境下的長距離帶狀控制網進行測試評估。

1 長距離帶狀控制網解算策略

1.1 基本方法

雙差模型可以對衛星的軌道誤差、衛星鐘差、接收機鐘差和大氣延遲等誤差進行消除和減弱,從而提高定位的精度[14-15]。設在GNSS標準時刻ti于測站1、2同時對衛星k、j進行測量,雙差觀測值模型可表示為[16-17]

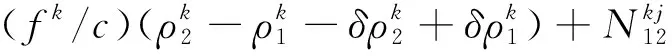
(1)

單天解標準化均方差(Normalized Root Mean Square,NRMS)表示單時段解算出的基線值偏離其加權平均值的程度。NRMS值可表示為

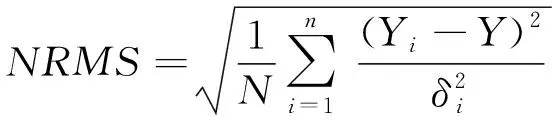
(2)

式中,N為測站個數;Yi為第i日的基線邊長;Y為單天解基線邊長的加權平均值;δi為單位權中誤差。GAMIT基線解算時,NRMS值一般要求小于0.3,如果NRMS大于0.5,說明周跳沒有完全修復,解算不合格[9]。

1.2 影響因子分析與優化策略

選取中國西部某省的5個CORS站點在2020年連續15 d的數據構成長距離帶狀控制網進行解算,測站之間的平均距離為83 km,如圖1所示。

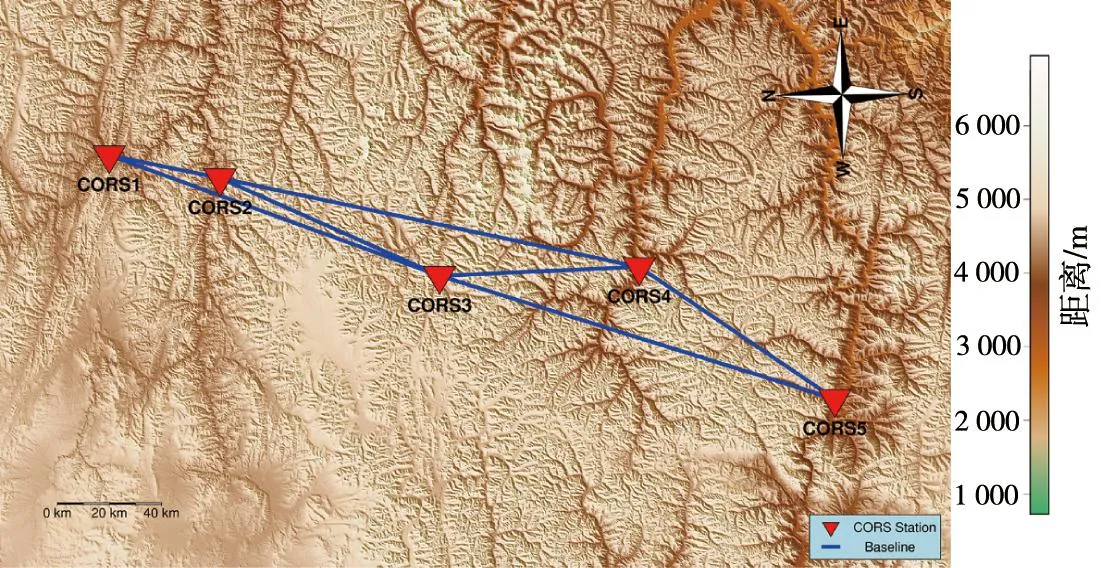
圖1 中國西部某省長距離帶狀控制網示意Fig.1 Schematic diagram of a long-distance strip control network in a province in western China

1.2.1 GNSS多星座數據分析

為對比不同星座對帶狀控制網基線解算的影響,選取帶狀控制網附近4個IGS站點(HKWS、URUM、LHAZ、JFNG)作為固定站進行平差計算,對單星座及多星座聯合解進行精度的比較。對比分析的星座組合有:單一GPS、單一BDS-2、單一GLONASS、GPS+BDS-2、GPS+GLONASS、GPS+BDS-2+GLONASS。統計各控制點在X、Y、Z方向平差后的點位精度,如圖2所示。單星座平差精度中,GPS星座在X、Y、Z方向上的平均精度最高,平均精度分別為1.0,3.08,1.82 mm;雙星座的平均精度中,GPS+BDS-2兩個星座在X、Y、Z方向上的平均精度最高,平均精度分別為0.8,2.38,1.34 mm,相較于單星座而言精度都有所提高。

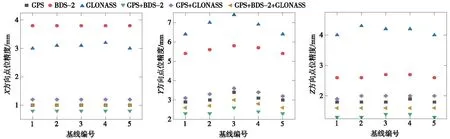
圖2 不同星座點位精度Fig.2 Point accuracy of different constellations

對基線平差計算后的坐標值進行分析,以GPS+BDS-2+GLONASS多星座平差坐標值作為參考基準,分別和其他方案的平差坐標值求差,結果如表1所示。當利用單星座系統進行平差計算時,從差值的最大值和最小值來看,由GPS星座解算的坐標值與參考基準最吻合;當利用雙星座系統進行平差計算時,GPS+GLONASS組合系統能得到最優結果,且雙星座系統都優于單星座系統。

1.2.2 觀測值類型選擇

基線解算中,雙頻GNSS觀測值可以構成不同的基線解類型[12],如表2所示。

表2 觀測基線解類型Tab.2 Observed baseline solution type

針對觀測值類型對帶狀控制網解算的影響,以NRMS值進行分析,如圖3所示。其中,LC_HELP解算15 d的NRMS值都小于0.3,滿足基線解算要求;L1_ONLY、L2_ONLY和L1,L2_INDEPENDENT三種基線解類型解算的15 d的NRMS值均大于0.5,說明這三種基線解類型無法滿足帶狀控制網基線處理的要求。因此,建議采用寬巷模糊度由電離層約束解算的線性組合觀測值。

圖3 觀測值類型NRMS值Fig.3 Observation type NRMS value

1.2.3 對流層和電離層延遲

對流層延遲和電離層延遲是基線解算中重要的誤差改正項,可采用模型改正和差分的方式消除。長距離帶狀控制網跨度大,大氣延遲的空間相關性降低,若采用差分方式,難以有效削弱,但大氣模型本身又存在模型誤差[8],如何選擇合理的大氣延遲改正方式是本文要探討的問題。基于此,本文利用模型改正和差分改正分別進行實驗,分析基線長度<100 km的帶狀控制網解算精度,結果如圖4、圖5所示。

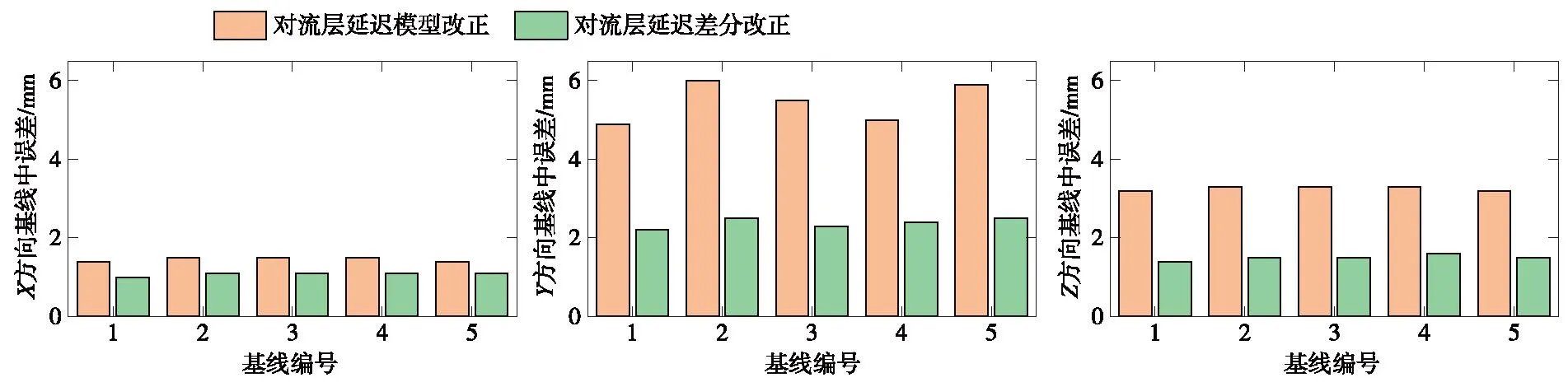
圖4 對流層延遲基線中誤差Fig.4 Error in tropospheric delay baseline

圖5 電離層延遲基線中誤差Fig.5 Error in ionospheric delay baseline

圖4中對流層延遲采用Saastamoinen模型(SAAS)改正處理后的基線X、Y、Z方向分量誤差均大于站間差分改正,所以站間差分改正對流層延遲效果更好。圖5中電離層采用高階電離層延遲模型(GMAP)改正和差分改正對于長距離帶狀控制網在X、Y、Z方向上解算效果基本相當,因此當基線長度在100 km以內時,帶狀控制網的電離層延遲使用模型改正和差分改正均可。

1.2.4 IGS測站約束

測站坐標約束是對一個或多個已知點坐標進行約束以求得未知測站精確坐標,對高精度的已知坐標需要進行強約束,待求點進行松弛約束[8-9]。本文對IGS站點進行緊約束,其余控制點進行松弛約束,以基線解算精度作為指標進行分析,實驗具體設置的不同約束方案如表3所示。

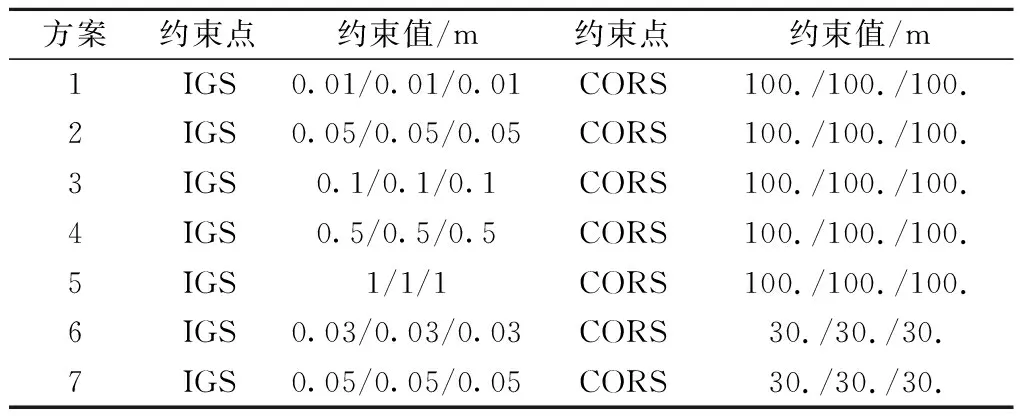
表3 約束方案設置Tab.3 Constraint scheme settings

針對IGS站點和控制點進行不同策略的緊約束和松弛約束,不同約束策略的NRMS值均小于0.3,基線解的結果可靠。圖6展示了不同方向的基線分量中誤差。可以看到,在X方向和基線長L上不同約束策略對基線解算精度影響顯著,其中對IGS站點進行0.01,0.03,0.05 m三種約束策略變化較小、精度較優;而對IGS站點進行0.1,0.5,1 m三種約束變化較大,且在X方向和基線長L上精度都很低。所以對于帶狀控制網使用0.01,0.03,0.05 m的測站坐標約束,可獲得較好的解算結果。

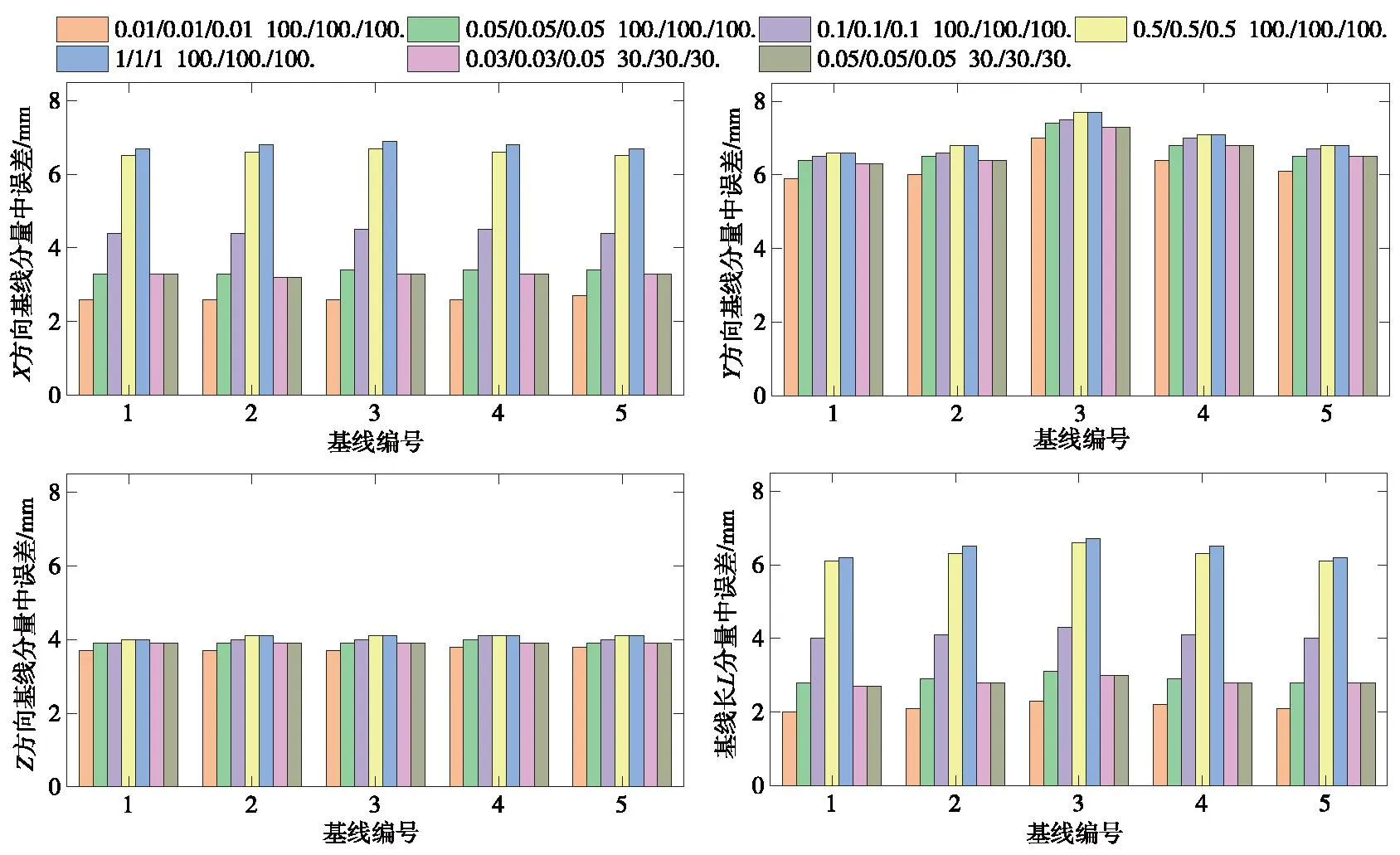
圖6 不同約束策略基線中誤差Fig.6 Error in baseline of different constraint strategies

1.2.5 海潮和大氣負荷模型

海洋潮汐是時序的負荷,海潮負荷會導致靠近海洋的區域產生厘米級的地表誤差,而大氣質量的不均勻會導致地球表層發生形變。考慮到中國地區部分IGS站點位于沿海地區,因此有必要分析海潮負荷和大氣負荷模型對長距離帶狀控制網解算精度的影響[18]。

海潮負荷和大氣負荷模型基線中誤差如表4所示。

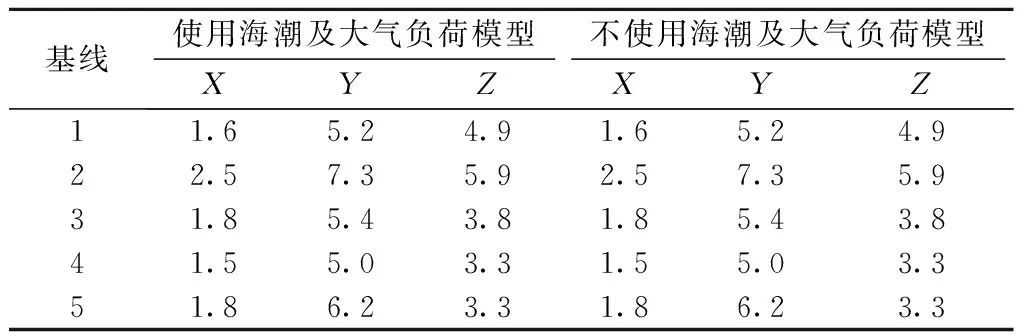
表4 海潮負荷和大氣負荷模型基線中誤差 mmTab.4 Errors in the ocean tide load and atmospheric load model baselines

由表4可知,全球海潮負荷模型和大氣負荷模型對內陸地區的帶狀控制網解算精度無影響,因此在高精度帶狀控制網解算中可結合實際環境條件和工程需求確定是否需要進行海潮和大氣負荷改正。

通過上述實驗分析,得出適用于鐵路工程長距離帶狀控制網的高精度解算策略,如表5所示,其中,衛星截止高度角參數由李建濤等[8-10]給出。

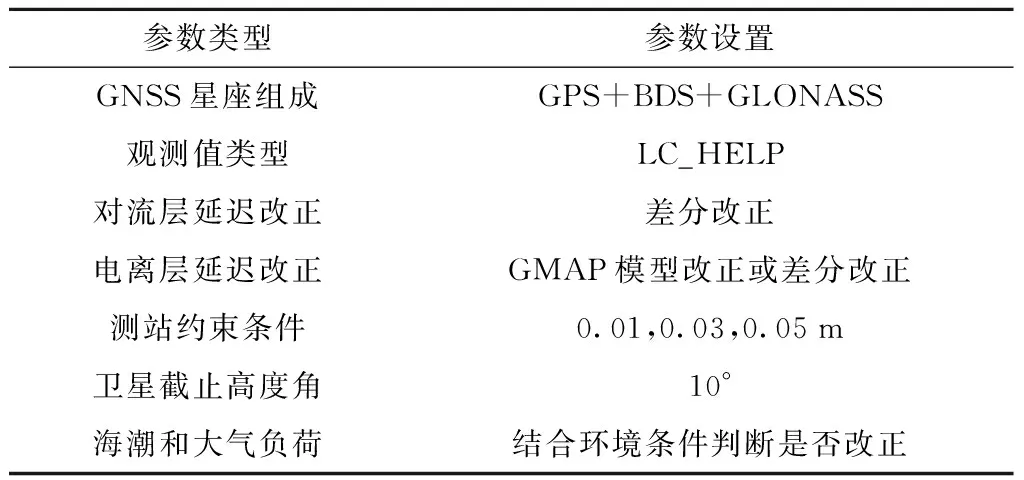
表5 鐵路工程長距離帶狀控制網高精度解算策略Tab.5 High-precision solution strategy for long-distance strip control network in railway engineering

2 復雜地形環境下長距離帶狀控制網優化策略試驗

2.1 某在建鐵路工程長距離帶狀控制網解算

根據實驗得出的長距離帶狀控制網優化解算策略,采用中國某在建鐵路帶狀控制網的4個CORS站點(KDZD、KXDQ、LDSW和TQSJ)及周邊3個IGS站點(JFNG、LHAZ和URUM)在2021年年積日81～85連續5 d的數據進行試驗,帶狀控制網示意如圖7所示。

圖7 某在建鐵路帶狀控制網CORS站點示意Fig.7 Schematic diagram of the CORS site of a railway strip control network under construction

為分析本文實驗得到的優化策略在處理長距離帶狀控制網的精度,分別統計默認策略和優化策略解算圖7中CORS站點構成的5條基線在X、Y、Z方向上的精度結果如圖8所示。從圖8中可以看出,默認策略處理長距離帶狀控制網相比優化策略在Y和Z方向精度都降低了2～5 mm,即優化策略比默認策略的解算精度更優。實驗也說明了本文得出的優化策略解算鐵路工程長距離帶狀GNSS控制網是可靠的。

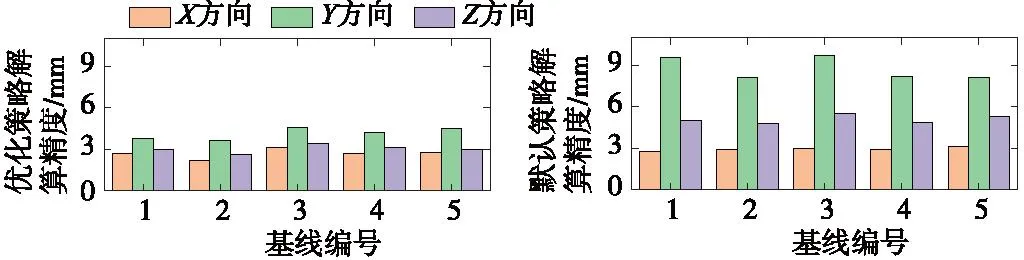
圖8 默認策略和優化策略基線解算精度Fig.8 Baseline solution accuracy of default strategy and optimization strategy

2.2 大高差區域帶狀控制網解算

復雜地形地貌區帶狀控制網高差大,高程異常變化顯著,該環境下的CORS站點更易受到板塊運動、地震等影響[20-21]。為測試本文提出的解算策略在復雜地形條件下的解算性能,利用SCCORS網部分測站,分別模擬鐵路工程在復雜地形環境下的不同海拔混合帶狀控制網,進行高精度基線解算試驗與精度分析。

采用川西25個CORS站點在2012年連續1年的GPS+GLONASS雙星座系統數據組成6條位于不同地形環境下的帶狀控制網如圖9所示,其中網1-1和網1-2位于川西高海拔地區,網2-1和網2-2橫跨成都平原和川西高海拔地區,網3-1和網3-2位于成都平原低海拔地區。

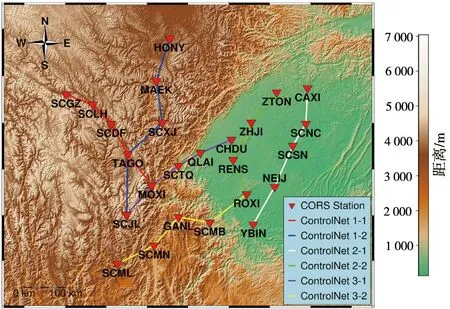
圖9 復雜地形環境長距離帶狀控制網CORS站示意Fig.9 Schematic diagram of CORS station for long-distance strip control network in complex terrain environment

選取6個IGS站點(BJFS、GUAO、LHAZ、SHAO、URUM和WUHN)作為固定站。圖10展示了采用優化策略解算復雜地形環境下的長距離帶狀控制網得到X、Y、Z方向的基線解中誤差,其中,MOXI站構成的5條基線(TAGO-MOXI、SCDF-MOXI、SCTQ-MOXI、MOXI-SCJL、QLAI-MOXI)和SCJL站構成的4條基線(TAGO-SCJL、SCXJ-SCJL、MOXI-SCJL、SCTQ-SCJL)解算誤差較大,對這2個測站進行檢核發現為原始觀測數據質量較差造成相關基線解算精度較低。因此,將上述9條基線作為粗差剔除后,統計剩余基線的解算精度為:高海拔地區基線平均精度為4.1 mm,低海拔地區解基線平均精度為3.8 mm,高低海拔混合地區基線平均精度為3.9 mm,均滿足TB 10601—2009《高速鐵路工程測量規范》對控制網基線處理質量檢核的相關要求[19]。

圖10 復雜地形環境長距離帶狀控制網基線解算精度Fig.10 Baseline solution accuracy of long-distance strip control network in complex terrain environment

利用平差軟件進行約束平差,得到各控制點的坐標精度,分別如表6～表8所示,從表中可知,長距離帶狀控制網在復雜地形環境下測站X、Y、Z方向精度平均值優于5 mm,不同方向精度較差在1 mm以內,其中高海拔地區X方向精度為2.9 mm,Y方向為8.5 mm,Z方向為4.9 mm;低海拔區X方向精度為3 mm,Y方向為7.4 mm,Z方向為4.3 mm;高低海拔混合區X方向精度為3 mm,Y方向為8.5 mm,Z方向為4.7 mm。其中MOXI站和HONY站相較于其他測站精度偏低,對數據進行檢核發現測站概略坐標偏差較大。其他測站精度符合《高速鐵路工程測量規范》對控制網平差的規定[19]。可見,本文得到的長距離帶狀控制網解算策略適用于復雜地形環境的基線解算。

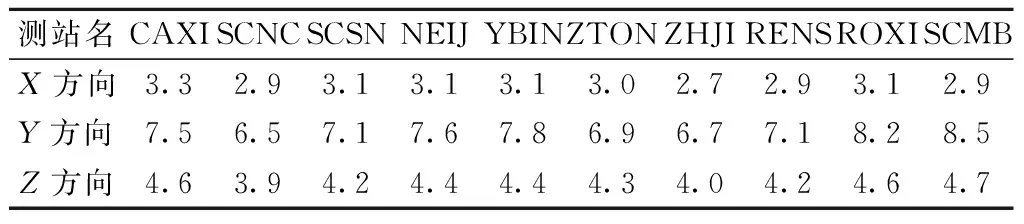
表7 低海拔帶狀控制網平差各方向中誤差 mmTab.7 Errors in all directions of low-altitude strip control network adjustment

表8 高低海拔混合帶狀控制網平差各方向中誤差 mmTab.8 Errors in each direction of high and low altitude mixed strip control network adjustment

3 結論

為提高鐵路工程GNSS帶狀控制網的解算精度,本文從GNSS星座數量、觀測值類型、大氣延遲校正、測站約束條件、海潮及大氣負荷等方面進行討論,篩選出適用于長距離帶狀控制網的優化解算策略,并結合實際測量數據進行測試分析,主要結論如下。

(1)在引入IGS站點坐標約束,對坐標分量設置≤ 0.05m的松弛約束,采用多星座衛星觀測數據,基于電離層約束求解寬巷模糊度,基線長100 km內的帶狀控制網對流層延遲采用站間差分改正、電離層延遲采用差分或模型改正,并結合實際環境條件加入海潮和大氣負荷改正,可獲得長距離帶狀控制網基線的最優解。

(2)在復雜地形環境下,采用優化策略解算長距離帶狀控制網,高海拔地區解算精度為4.1 mm,低海拔地區解算精度為3.8 mm,高低海拔混合地區解算精度為3.9 mm,精度水平相當,均滿足工程測量相關規范要求。