GeoGebra軟件在高中物理教學中的應用
——以“蠟塊的運動”演示實驗為例

魏代文

(沂水縣第三中學 山東 臨沂 276400)

鄭萌萌

(曲阜師范大學物理工程學院 山東 濟寧 273165)

“蠟塊的運動”是新人教版教材“運動的合成與分解”一節中的演示實驗.合運動與分運動兩個概念的建立、合運動與分運動關系的學習、互成角度兩個直線運動的合運動的性質與軌跡的探究都基于本實驗.該實驗對學生學習與構建運動合成與分解知識,體會與培養等效思想和化繁為簡思想有著重要作用.同時還為后續復雜曲線運動的處理做了方法上的鋪墊.

GeoGebra是一款動態數學軟件,具有極佳的動態性,非常適合用來演示數學、物理、工程上面的很多現象和知識[1].因此,本文詳細介紹了運用GeoGebra軟件制作“蠟塊的運動”動態演示圖的過程,以期能讓學生更加直觀、深入地了解和學習運動的合成與分解,也期望能為一線教師同仁提供教學參考.

1 蠟塊的運動實驗和原理

1.1 蠟塊的運動實驗簡介

如圖1所示,在注滿清水的玻璃管內,放有一紅蠟塊A,將玻璃管的開口端用橡膠塞塞緊[圖1(a)].把玻璃管倒置[圖1(b)],蠟塊A會沿玻璃管上升,大致做勻速直線運動.在蠟塊勻速上升的同時,將玻璃管沿水平方向向右勻速移動[圖1(c)][2].

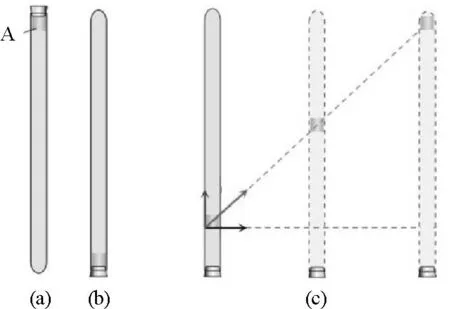
圖1 蠟塊的運動實驗示意圖

1.2 蠟塊的運動實驗原理

在圖1(c)中,蠟塊的實際運動為相對于紙面向右上方的運動,即合運動;在蠟塊的實際運動中既參與了玻璃管水平向右平移的運動,又參與了沿玻璃管上升的運動,即水平向右的分運動和沿管向上的分運動.

由合運動與分運動的關系可知,分運動之間相互獨立互不影響.以蠟塊初始位置(蠟塊的左下角)為坐標原點O建立直角坐標系,若蠟塊在水平方向上有初速度vx0,也有加速度ax,則蠟塊在水平方向的分速度

vx=vx0+axt

在水平方向上的分位移

同理若蠟塊在沿管方向上有初速度vy0,也有加速度ay,則蠟塊在沿管方向的分速度

vy=vy0+ayt

在沿管方向上的分位移

又因為運動的合成與分解實質為位移、速度、加速度的合成與分解,且合運動與分運動之間滿足矢量運算的平行四邊形定則,設合速度為v,合位移為s,則分運動與合運動關系滿足圖2所示的平行四邊形定則.

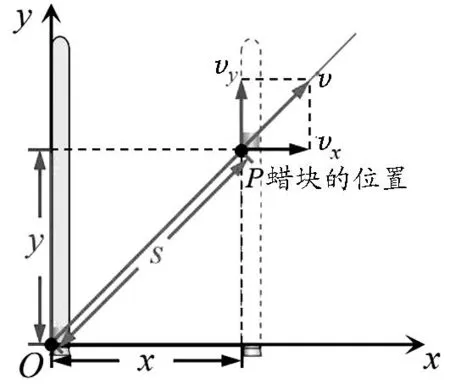
圖2 蠟塊運動的速度和位移

2 蠟塊的運動動態模擬課件的開發

2.1 相關參數及控制按鈕的創建

選擇滑動條工具,創建蠟塊運動的5個參數:運動時間t、蠟塊水平初速度vx0、蠟塊水平加速度ax、蠟塊沿管初速度vy0、蠟塊沿管加速度ay.選擇輸入框工具,建立5個輸入框并分別關聯到滑動條t、vx0、ax、vy0、ay.分別默認vx0=1.5、ax=0、vy0=2、ay=0(各物理量單位默認為國際單位).

代數區輸入a=true.選擇按鈕工具,建立按鈕button1、button2.設置button1腳本代碼為:啟動動畫(t,a);設置標題(button1,如果(a,"暫停","開始"));賦值(a,a).button2腳本代碼為:設置標題(button2,"復位");賦值(t,0);放大(1).兩個按鈕將用來控制運動的開始和暫停、復位.效果如圖3所示.

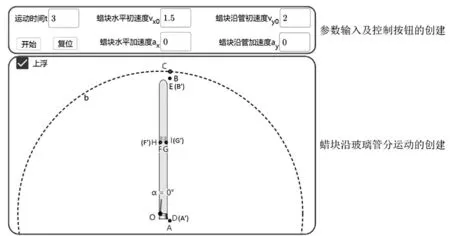
圖3 相關參數、控制按鈕及蠟塊沿玻璃管分運動的創建

2.2 蠟塊沿玻璃管分運動的創建

代數區輸入“A=(x(O)+0.8,y(O)-0.6)、B=(x(A),y(A)+12)”.選擇圓(圓心與半徑)工具,以坐標原點O為圓心,12為半徑做圓b.選擇對象上的點工具,在圓b上任選一點C.選擇角度工具,依次點擊B、O、C得到角α.如圖3所示,C點將用來控制調整玻璃管和蠟塊的傾斜角度.

選擇旋轉工具,將點A和點B繞點O逆時針旋轉α角度,得到點A′和點B′.插入玻璃管圖片pic1,將控制玻璃管大小的兩點D、E分別與A′、B′關聯.代數區輸入“F=(x(O),y(O)+vy0t+1/2ayt2)”“G=(x(F)+0.5,y(F))”.選擇旋轉工具,將點F和點G繞點O逆時針旋轉α角度,得到點F′和G′.插入蠟塊圖片pic2,將控制蠟塊大小的兩點H、I分別與F′、G′關聯.

選擇復選框工具,將標題設為“上浮”,選擇的對象為點F′、圖片pic1、圖片pic2,此時自動生成布爾值c.該復選框將用來顯示或隱藏蠟塊沿玻璃管分運動的動畫.效果如圖3所示.

2.3 蠟塊水平分運動與合運動的創建

插入玻璃管圖片pic3,將控制玻璃管大小的兩點J、K分別與A′、B′關聯.代數區輸入“L=(0,0)、M=(x(L)+0.5,y(L)).”選擇旋轉工具,將點L和點M繞點O逆時針旋轉α角度,得到L′和M′.插入蠟塊圖片pic4,將控制蠟塊大小的兩點N、P分別與L′、M′關聯.插入玻璃管圖片pic5,將控制玻璃管大小的兩點Q、R分別重新定義,輸入“Q=(x(A′)+vx0t+1/2axt2,y(A′))、R=(x(B′)+vx0t+1/2axt2,y(B′))”.代數區輸入“S=如果(c,(x(L′)+vx0t+1/2axt2,y(L′)),(x(F′)+vx0t+1/2axt2,y(F′)))”.代數區輸入“T=如果(c,(x(M′)+vx0t+1/2axt2,y(M′)),(x(G′)+vx0t+1/2axt2,y(G′)))”;插入蠟塊圖片pic6,將控制玻璃管大小的兩點U、V分別與S、T關聯.輸入“W=(x(L′)+vx0t+1/2axt2,y(L′))”.此時蠟塊水平分運動與合運動創建完畢.

選擇復選框工具,將標題設為平移,選擇的對象為點L′、點S、點W、圖片pic3、圖片pic4、圖片pic5、圖片pic6,此時自動生成布爾值d.該復選框將用來顯示或隱藏蠟塊水平分運動與合運動的動畫.當布爾值c為假(即不選中上浮標簽時,選中平移標簽時),課件只顯示蠟塊水平分運動,效果如圖4(a)所示;當布爾值c為真,d為真(即選中上浮標簽和平移標簽時),課件顯示蠟塊合運動,效果如圖4(b)所示.

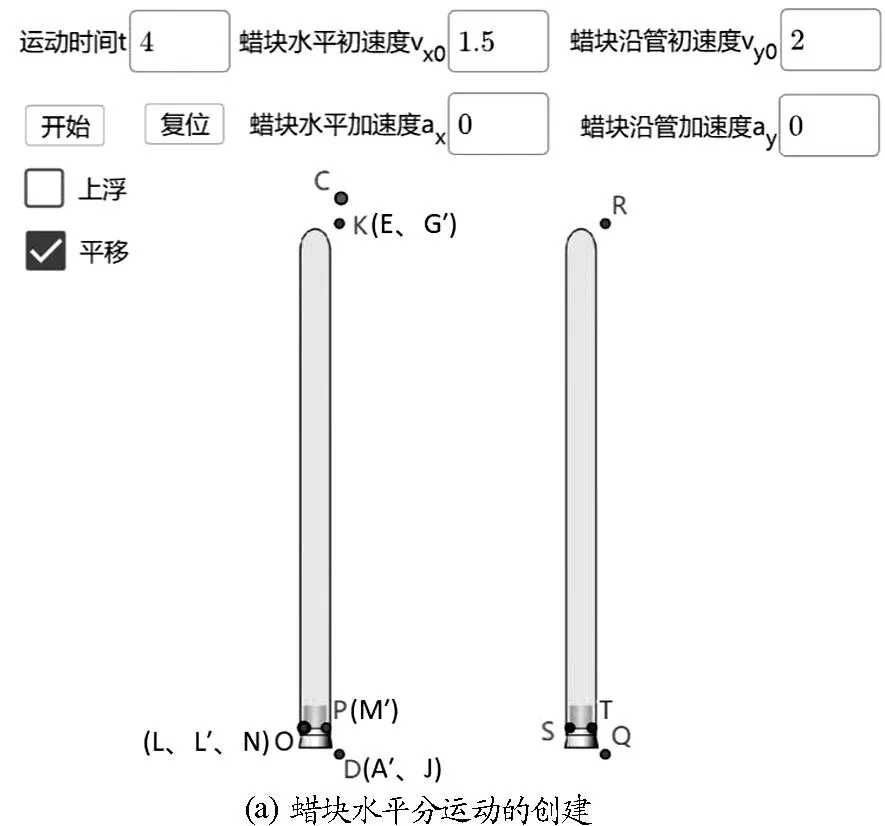
圖4 蠟塊水平分運動與合運動的創建

2.4 相應運動參量的展示創建

選擇線段工具,作線段L′F′、L′W、L′S、F′S、WS,改變線段F′S、WS樣式為虛線.并將線段L′F′、L′W、L′S標題分別設為“y”“x”“s”.選擇復選框工具,設置標題為“x”,選定對象為L′W,用以顯示和隱藏表示蠟塊沿水平運動的位移線段.同理作出表示蠟塊沿管運動的位移線段“y”、蠟塊實際運動的位移線段“s”以及位移合成的平行四邊形的“邊”.

代數區輸入“X=(x(S)+vx0+axt,y(S))、Y=(x(S),y(S)+vy0+ayt)”.選擇旋轉工具,將Y點繞點S旋轉α角度得到點Y′.選擇向量工具,點擊點S和點X創建向量u,點擊點S和點Y′創建向量v,并分別命名為“vx”“vy”.選擇平行線工具,過點X作向量v的平行線,過點Y′作向量u的平行線.選擇交點工具,點擊兩條平行線得到兩條平行線的交點Z.選擇線段工具,作線段Y′Z、XZ,設置樣式為虛線.選擇向量工具,點擊點S和點Z創建向量w,并設置標題為“v”.

選擇復選框工具,設置標題為“v”,選定對象為向量u、向量v、向量w、線段Y′Z、XZ.用以顯示或隱藏速度的平行四邊形合成.

最后隱藏不必要的點和標簽,顯示點F′、S、W的軌跡,并對課件進行美觀優化,最終效果圖如圖5所示.

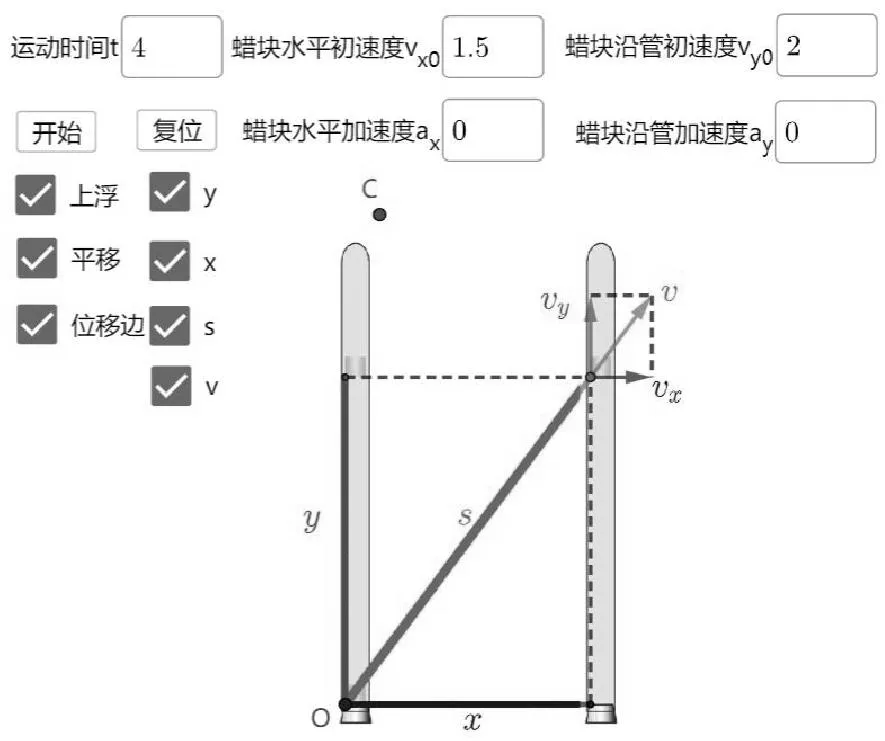
圖5 蠟塊的運動最終效果圖

3 蠟塊的運動實驗動態模擬課件的演示

至此,我們詳細介紹了用GeoGebra制作“蠟塊的運動”演示實驗的過程,讀者可通過本文以上介紹獨立制作直觀化并且比較優美的“蠟塊的運動”演示實驗課件.本課件可實現以下幾種功能:

(1)輔助教材“蠟塊的運動”演示實驗的教學

1)分步展示蠟塊的分運動.首先,拖動點C讓角α=0°,使得玻璃管呈現豎直狀態;然后,選中“上浮”和“y”標簽,點擊開始按鈕,展示蠟塊沿管的豎直分運動動畫,如圖6(a)所示;最后,取消選中“上浮”和“y”標簽,選中“平移”和“x”標簽,點擊開始按鈕,展示蠟塊水平分運動動畫,如圖6(b)所示.

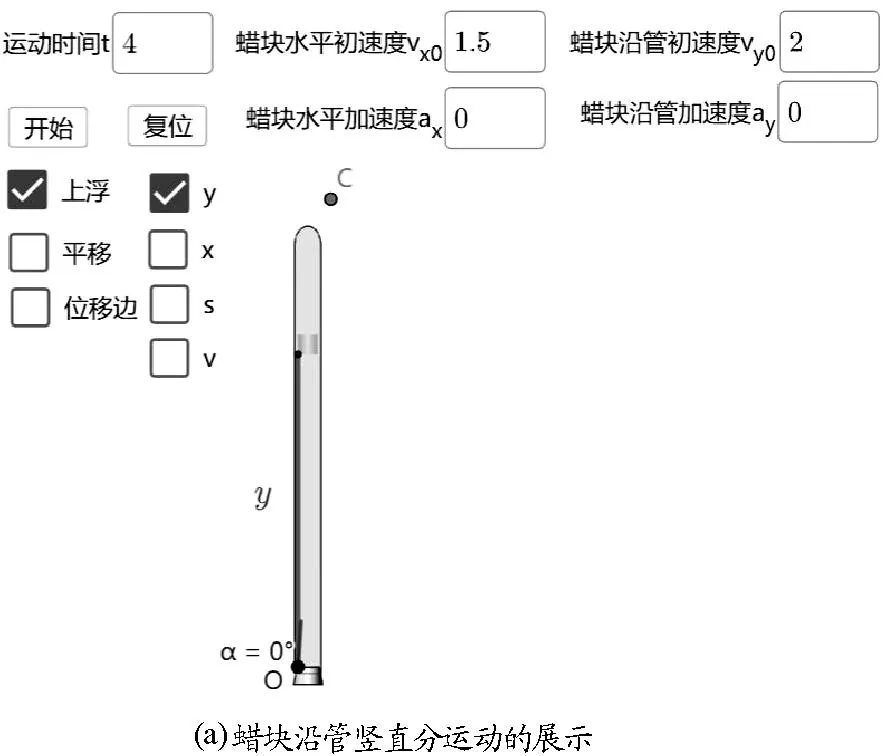
圖6 蠟塊沿管分運動的演示

2)綜合展示蠟塊的合運動.保持角α=0°,將標簽全部選中,點擊開始按鈕,展示蠟塊的合運動動畫,如圖7所示.

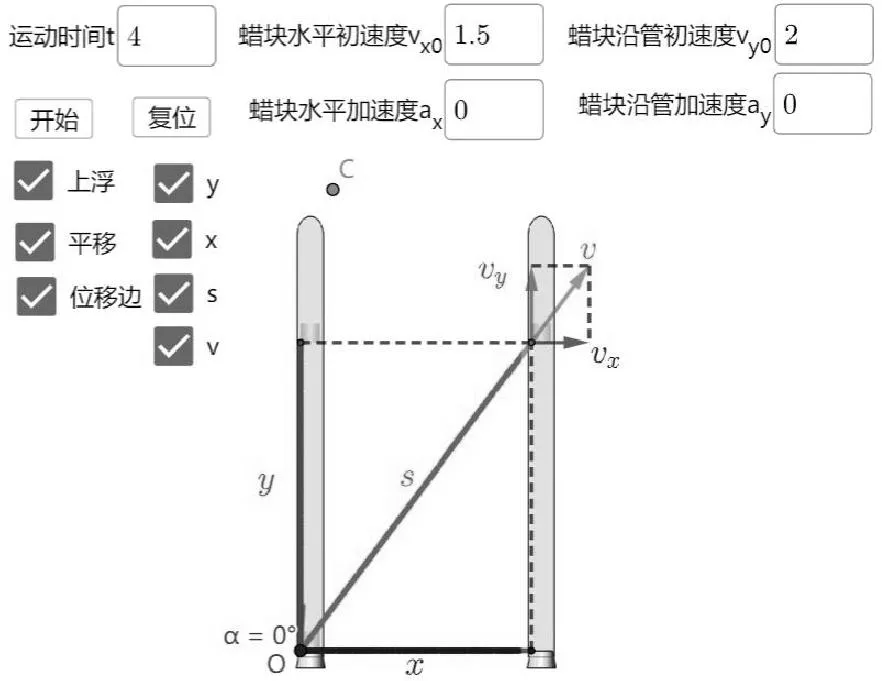
圖7 蠟塊合運動的演示

(2)探究互成任意角度的兩個直線運動的合運動性質和軌跡

互成任意角度的兩個直線運動的合成有如表1所示的幾種情況.

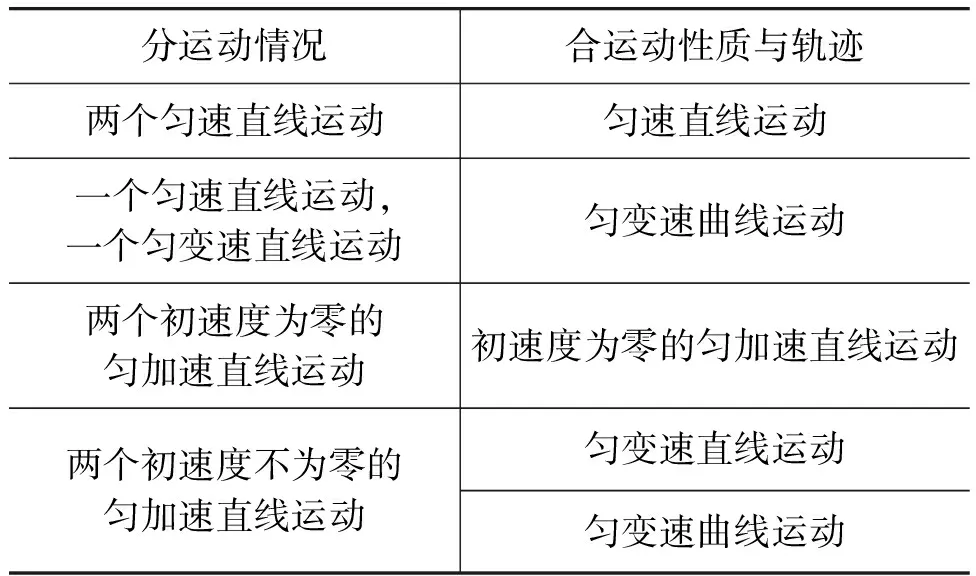
表1 互成任意角度的兩個直線運動合成幾種情況

本課件可一一將上述幾種情況進行展示,由于篇幅原因下文僅詳細介紹“一個勻速直線運動,一個勻變速直線運動的合成”展示過程.

默認兩分運動互相垂直(此時α=0°),且蠟塊在沿管方向上做勻速直線運動,在水平方向上做勻加速直線運動.首先,保持原默認數值,將蠟塊水平加速度ax設為0.3;然后,選中全部標簽,設置點S顯示軌跡;最后,點擊開始按鈕,進行動畫展示,如圖8所示.

圖8 勻速直線運動和勻變速直線運動合成展示

由圖8可知蠟塊實際運動軌跡s′與位移s不重合,結合理論分析可知一個勻速直線運動和一個勻變速直線運動的合運動為勻變速曲線運動,軌跡彎向物體的加速度方向.

4 總結

本文利用GeoGebra的動態演示功能,開發了一個動態模擬“蠟塊的運動”演示實驗的課件,能夠實現蠟塊運動過程的可視化.在此基礎上,通過全參數可調來探究互成角度的兩直線運動的合運動性質與軌跡.另外,課件還可用于探究速度、加速度的變化對蠟塊實際運動軌跡的影響.

GeoGebra功能強大,應用范圍非常廣泛,正版免費,不需要編程基礎,簡單易學,做出的課件對教學難點的破解作用很大[3].通過本課件的開發,希望能為一線教師同仁提供一些教學參考,同時也可以根據自身需要對本課件進行二次開發拓展,制作出更加優秀的課件服務教學.