機動載荷對彈用渦輪發動機轉子動力學特性的影響

賈勝錫，陳俊屹，張 皓，顏 密，田小濤

(西安現代控制技術研究所，陜西 西安 710065)

0 引言

對彈箭武器而言,機動性是武器突防能力的體現。機動飛行時,轉子系統會隨著機體的運動而產生基礎運動,發動機本身還在轉動,如此就會產生附加的陀螺力矩,此外不同的機動動作還會產生其他機動載荷,如附加離心力、慣性力、剛度效應和阻尼效應等。對于彈用渦輪發動機的轉子系統,這些載荷的影響尤其突出[1-2]。

早期國外對機動飛行轉子動力學的研究始于一系列飛行試驗,主要是為了解決型號轉子振動問題。如波音公司的商務飛行試驗[3];Sherf等對F15戰機轉子的仿真研究[4];Spence等對直升機轉子與機身的耦合問題的研究[5];Ananthan對直升機轉子在戰術飛行時動力學響應的研究[6]等。這些研究表明,機動飛行會影響轉子系統的正常工作,特別是響應特性和穩定性。

一般而言,機動飛行帶來的附加載荷可以看作是對基礎的激勵,因此可以通過基礎激勵研究機動飛行狀態下的轉子特性。Duchemin等研究了柔性轉子在基礎位移激勵下的動力學行為,利用拉格朗日方程和瑞利-里茲法分析了臨界轉速附近的轉子彎曲特性[7]。Fawzi等研究了諧波激勵下剛性轉子的動力學行為[8]。Sakata等分析了基礎轉動狀態下柔性懸臂轉子的穩態響應特性[9]。徐敏等以雙盤懸臂轉子為對象,研究了水平盤旋、俯沖拉起時的動力學特性[10]。林富生等對Jeffcott轉子以飛機在鉛垂面和水平面內做恒定角速度、恒定加速度為運動條件研究機動對轉子振動的影響規律[11]。祝長生等利用Lagrange方程詳細推導了任意機動下多盤轉子的動力學方程[12-13]。Hou等研究了機動飛行狀態下轉子系統的非線性行為[14]。以上理論研究的對象都是簡單模型轉子,只能得到定性的結論。然而,真實發動機轉子結構復雜,要準確分析復雜轉子在機動飛行狀態下的動力特性,有必要發展有限元法。

鑒于以上問題,文中從相對運動的角度出發,建立了非慣性系中轉子系統的運動方程,相比于拉格朗日方法,可以更清楚揭示機動載荷的來源;在此基礎上,給出了基于有限元法的轉子動力學特性分析方法,計算分析了機動載荷對轉子系統響應的影響。

1 機動飛行轉子動力學方程

1.1 轉子模型與坐標系

運用相對運動原理建立機動飛行狀態下轉子動力學方程。

彈用渦輪發動機一般為小推力渦噴發動機和小涵道比渦扇發動機,其轉子系統通常由2～3級離心壓氣機或離心與軸流組合壓氣機,與單級向心渦輪組成,采用懸臂或簡支結構。為了研究轉子動力學的基礎問題,使模型及計算方法更具通用性,以居中盤轉子和懸臂盤轉子為例,采用如圖1所示的坐標系。以地面固定坐標參考系OXYZ來描述彈體重心的平移運動以及彈體坐標系oxyz描述彈體的轉動,假設機體的重心和轉子一端重合,彈體坐標系即是轉子坐標系。

圖1 轉子模型及坐標系Fig.1 Structure of rotor and coordinate system

1.2 轉子動力學方程

現在分析軸向位置為(x,y,zi)的轉盤運動情況。轉子系統在機動飛行情況下可以看成是一個轉動非慣性系,而x或y方向上的振動可以看成相對于轉子坐標系的平動運動,根據理論力學基本知識可建立盤心相對于轉子坐標系的平動運動微分方程[15]:

miar=F-miae-miac=F+FIe+FIC

(1)

式中:ar為相對運動加速度;F為轉子系統受到的合力;FIe為牽連慣性力;FIC為盤心a點的哥氏慣性力;ae為牽連加速度,其定義由下文推導給出。

盤心的速度可表示為:

v=ω×r=(ωxi+ωyj+ωzk)×
(xi+yj+zik)=(ωyzi-ωzy)i+
(ωzx-ωxzi)j+(ωxy-ωyx)k

(2)

式中ωx,ωy,ωz表示機動的角速度。式(2)對時間求導數可得加速度a:

a=α×r+ω×v=α×r+ω×(ω×r)

(3)

忽略z方向(軸向)振動,則x方向、y方向的牽連慣性力可表示為:

(4)

哥氏慣性力可表示為:

(5)

轉子非慣性系中的受力還包括:圓盤處軸剛度作用的彈性力Fk、阻尼力Fc、偏心質量引起的不平衡力Fu以及由于空間機動飛行所產生的力FR。

機動飛行轉子動力學方程通過聯合質心運動定理和相對質心的動量矩定理來建立。剛體運動的微分方程為[15]:

(6)

機動時,轉盤所受的慣性加速度與機體質心處的加速度相等,因此,慣性力與FR大小相等方向相反,其值等于慣性加速度和盤質量的乘積。將式(4)和式(5)以及式(6)前3項代入式(1)中,就可得到式(7)中的前兩個方程。轉子隨飛機旋轉會產生慣性力矩。將慣性力矩加到轉子振動的旋轉自由度中,就得到式(7)中的后兩個方程。

(7)

1.3 機動飛行產生的附加載荷

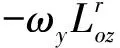
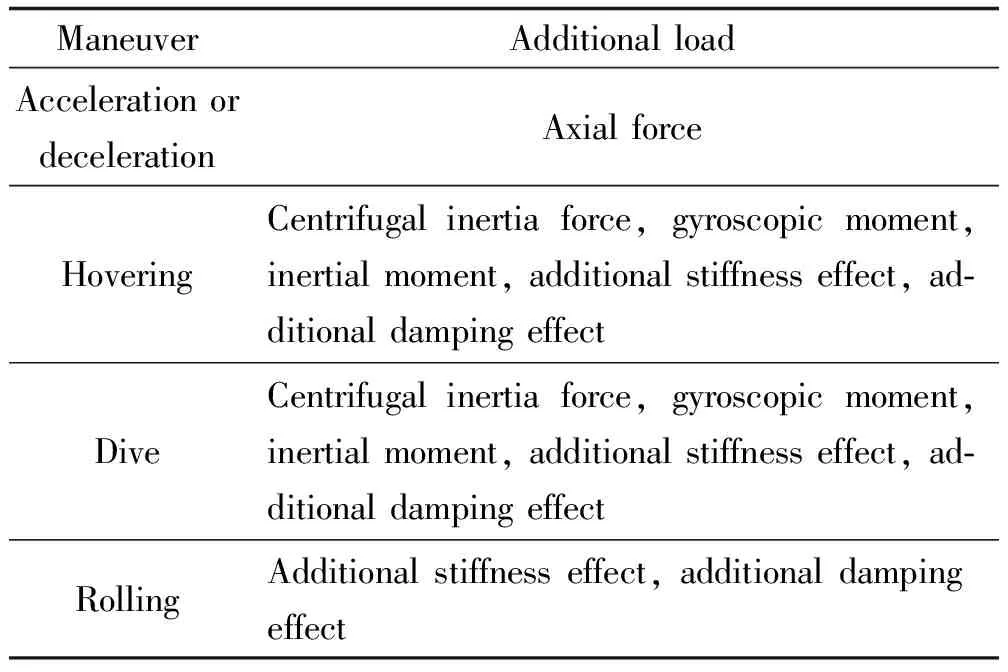
表1 典型機動飛行帶來的附加載荷Table 1 Additional loads caused by typical maneuvers

2 機動載荷的影響

借助轉子動力學有限元計算軟件SAMCEF/Rotor研究典型機動對轉子動力學特性的影響。

2.1 初始轉子動力特性

首先計算初始狀態的動力特性,即僅有不平衡量載荷作用下的轉子特性。轉子模型見圖1。轉軸長800 mm,半徑為15 mm。圓盤厚度為15 mm,半徑為50 mm。左右支承剛度為5×106N/m,各作用阻尼為500 N/(m/s)。材料屬性為:密度為7 800 kg/m3、泊松比為0.3、彈性模量為2×1011Pa。居中盤轉子的轉盤位于中間,懸臂盤轉子的右支承位于中間。不平衡量載荷設置為0.1 mm的質量偏心,工作轉速設定為6 000 r/min。圖2給出了在SAMCEF/Rotor中對居中盤轉子系統的動力學特性的計算結果。從圖中可以看出,轉子系統的臨界轉速為4 454.4 r/min,達到該轉速時,轉子系統的瞬態響應為1.52 mm,經過臨界轉速后,達到6 000 r/min的工作轉速時,轉子系統的穩態響應為0.063 mm。表2給出了兩種轉子結構臨界轉速、穩態響應和瞬態響應計算結果匯總。

表2 轉子系統初始動力學特性Table 2 Influence of aerodynamic load

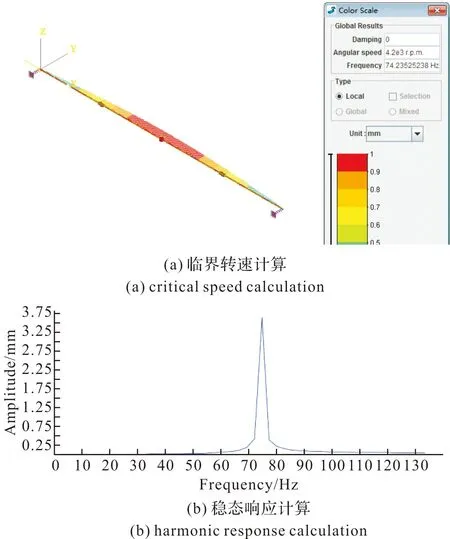
圖2 居中盤轉子系統初始動力學特性Fig.2 Initial dynamic characteristics of the center disk rotor system

2.2 橫滾機動的影響

機動載荷只是在彈體飛行過程中某一瞬時的動作,在轉子啟動過程中一般不會進行機動。因此,本節只研究了機動載荷對轉子系統穩態響應的影響,并設定機動發生時,轉子以工作轉速運行。

橫滾機動會給轉子系統帶來附加剛度效應和附加阻尼效應。其中附加剛度由轉盤質量mi與盤旋θy或俯沖角速度θx的平方之積確定,相較于轉子本身的剛度很小,計算時忽略這一影響。所產生的附加阻尼效應為交叉阻尼項cyx與cxy,其大小為-2miωz,2miωz,交叉阻尼項與主阻尼項可能處于同一數量級。對于居中盤轉子,假定機動時以3 r/s的速度進行橫滾,因此其橫滾角速度設定為20 rad/s,所產生的附加交叉阻尼以40 N/(m/s)計算,實際計算了5組交叉阻尼,分別為40 N/(m/s),100 N/(m/s),200 N/(m/s),500 N/(m/s)和1 000 N/(m/s)。

表3給出了加載5組交叉阻尼對轉子系統臨界轉速的影響,可以看出,在交叉阻尼為主阻尼8%～200%范圍內變化時,轉子臨界轉速會在-0.08%～0.34%范圍內響應變化,這一變化很小,因此可以忽略橫滾產生的交叉阻尼對轉子臨界轉速的影響。

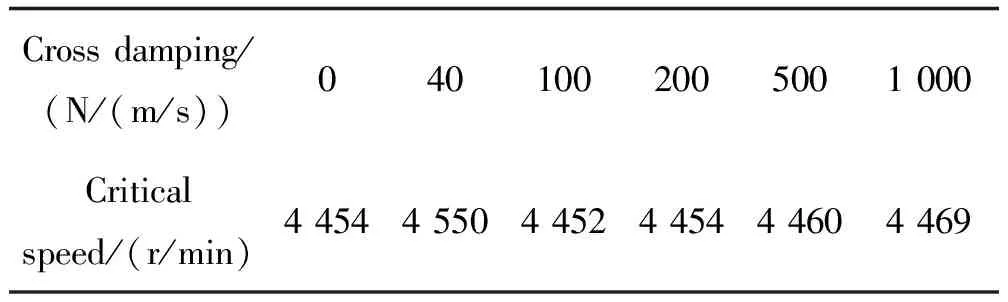
表3 交叉阻尼對臨界轉速的影響Table 3 Effect of cross damping on critical speed

圖3給出了加載5組交叉阻尼對轉子系統在工作轉速附近的穩態響應的影響。轉子系統在工作轉速上的穩態響應會隨著交叉阻尼的增大而減小。當由橫滾機動產生的交叉阻尼為主阻尼的200%時,轉子在工作轉速上的穩態響應降低了1.6%。這一影響相對于轉子整個轉速范圍內的響應很小,可以忽略。

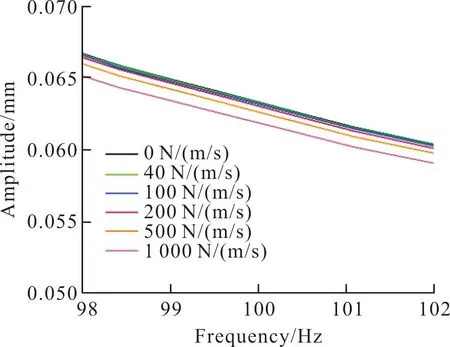
圖3 交叉阻尼對穩態響應的影響Fig.3 Effect of cross damping on harmonic response

以上給出的是正向橫滾機動的數值計算結果,也就是指轉子旋轉方向與飛行旋轉方向一致;反之,則為反向橫滾機動。對于反向橫滾機動,其產生的交叉阻尼與正向機動的交叉阻尼正好符號相反,其影響是增大穩態響應的振幅,但是增大的幅度依然很小。

2.3 常規機動

常規機動是指盤旋或俯沖拉起,其最大的特點是會產生附加陀螺力矩載荷和離心力載荷。除此以外還有附加剛度效應和附加阻尼效應及慣性力矩。

機動產生的陀螺力矩為[15]:

M=Ipω×Ω

(8)

式中:Ip為發動機轉子對旋轉軸向的轉動慣量;ω和Ω分別表示轉子繞軸的旋轉角速度和機體機動的角速度。盤旋機動和俯沖拉起機動給轉子系統帶來的附加載荷性質一樣,只是不同的機動載荷方向不一樣。

鑒于前文分析,附加剛度效應和附加阻尼效應不再考慮。機動載荷產生的慣性力矩是由機動角加速度引起的,其大小為轉子繞軸的直徑轉動慣量與角加速度的成積,其作用形式與陀螺力矩一樣,也是產生彎矩作用,兩種彎矩的作用方向相互垂直。可認為陀螺力矩中機動角速度和轉子繞軸轉動慣量的乘積與慣性力矩中機動角加速度和直徑轉動慣量的乘積處于同一數量級,這樣慣性力矩就比陀螺力矩小幾個數量級。因此,在水平盤旋機動中,重點考慮陀螺力矩和附加慣性力的影響。

根據文獻[16]中對機動載荷大小的規定,數值模擬時載荷大小設定為:3.5 rad/s的機動角速度疊加過載系數為1g的附加離心力。

圖4給出了加載機動陀螺力矩后轉子的變形。由圖4可知,陀螺力矩對轉子產生彎矩的作用,對于對稱轉子而言,陀螺力矩產生的變形與轉子的二階振型一致,盤剛好處于節點上,不產生盤心偏移。四分之一軸處的變形最大,其數值為0.002 mm,相比于轉子穩態響應的振幅,該值也比較小;對于懸臂轉子而言,陀螺力矩產生的變形與轉子的一階振型一致,盤處的產生的偏移量最大,其數值為0.055 mm。

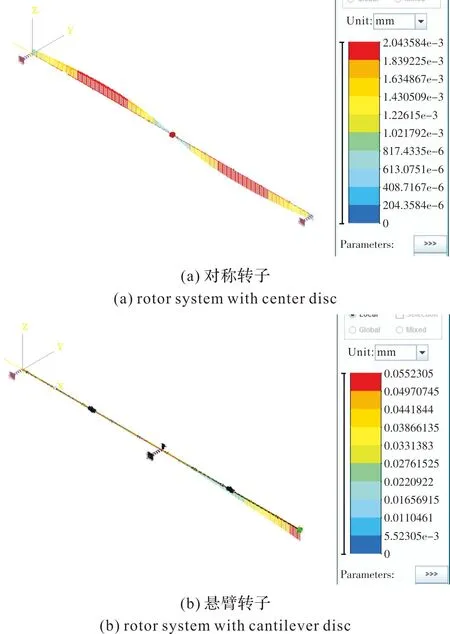
圖4 陀螺力矩的影響Fig.4 Effect of gyroscopic moment

圖5給出了加載附加離心力后轉子的變形。圖5結果表明,附加離心力載荷以體積力的形式作用于轉子,無論是對稱轉子還是懸臂轉子,盤處產生的偏移都最大。對于對稱轉子,附加離心力引起的盤心偏移量為0.055 mm,與工作轉速處的穩態響應處于同一個數量級,但遠小于其臨界轉速時響應幅值。對于懸臂轉子,附加離心力引起的盤心偏移量為0.121 mm,比工作轉速處的穩態響應大,增加了轉子發生碰磨的可能。為了便于對比,圖6給出了兩種載荷共同作用下轉子穩態響應的軸心軌跡。

圖5 附加離心力的影響Fig.5 Effect of additional centrifugal force

圖6 陀螺力矩和附加離心力對穩態響應的影響Fig.6 Influence of gyroscopic moment and additional centrifugal force on steady-state response of rotor

3 結論

針對機動飛行帶來的轉子動力學問題,運用質點相對運動原理建立了機動飛行轉子的運動方程,并通過方程分析了機動飛行給轉子系統帶來的載荷,借助有限元計算研究了機動飛行轉子的動力學特性,得到以下主要結論:

1)橫滾機動對轉子系統產生附加交叉阻尼項,影響轉子系統的臨界轉速和穩態響應。反向機動會增大轉子在工作轉速時的穩態響應,正向機動會減小轉子在工作轉速時的穩態響應,但這些影響都很小,可以忽略。

2)常規機動,即盤旋或俯沖拉起,會給轉子系統帶來附加陀螺力矩和附加離心力載荷。附加陀螺力矩對轉子產生彎矩作用,附加離心力載荷對轉子產生體積力作用,兩種載荷會造成與轉子工作轉速時穩態響應相當的盤心偏移,這會增加轉子發生碰磨的可能性。

需要注意的是,文中機動載荷大小的確定參考的是航空渦輪發動機相關標準,對于彈用渦輪發動機,其機動載荷會比航空渦輪發動機大,因此機動載荷對轉子動力學特性的影響需要根據實際情況評估。