透平式能量回收一體機(jī)水潤滑轉(zhuǎn)子穩(wěn)定性研究

寧延強(qiáng)，李 巖，張德勝，葉曉琰，丁競飛

（江蘇大學(xué) 國家水泵及系統(tǒng)工程技術(shù)研究中心，江蘇鎮(zhèn)江 212013）

0 引言

海水淡化高壓泵與能量回收一體機(jī)［1-2］是膜法海水淡化系統(tǒng)節(jié)約能源、降低成本的核心部件。通過將泵葉輪與透平葉輪同軸連接，泵端提供超高壓海水，為海水通過半透膜提供必要條件，未通過半透膜的高壓濃鹽水則流入透平端，推動透平葉輪旋轉(zhuǎn)回收其壓力能。一體機(jī)主軸采用水潤滑軸承支撐，相比油潤滑更為環(huán)保、經(jīng)濟(jì)，但由于水的黏度較低，因此對設(shè)計要求則更高。由于一體機(jī)要在高轉(zhuǎn)速下運行［3］，而水潤滑軸承-轉(zhuǎn)子系統(tǒng)［4-6］作為一體機(jī)的核心部件，對保障一體機(jī)的平穩(wěn)運行起著至關(guān)重要的作用。

一體機(jī)的工作轉(zhuǎn)速高達(dá)20 000 r/min，且水潤滑形成條件苛刻，因此一體機(jī)中水潤滑轉(zhuǎn)子系統(tǒng)的穩(wěn)定性分析［7-9］不可忽視。而對一體機(jī)中水潤滑轉(zhuǎn)子系統(tǒng)的研究僅停留在由單個水潤滑滑動軸承支撐，而未考慮口環(huán)間隙中水膜產(chǎn)生流體動壓潤滑效應(yīng)對一體機(jī)內(nèi)部轉(zhuǎn)子穩(wěn)定性及臨界轉(zhuǎn)速的影響。目前對轉(zhuǎn)子的穩(wěn)定性判斷有多種方式，主要包括實驗及數(shù)值計算。侯峰等［10］對雙螺桿制冷壓縮機(jī)轉(zhuǎn)子軸心軌跡波動特性進(jìn)行了試驗研究；葉曉琰等［11］研究了不同半徑間隙下水潤滑軸承軸心軌跡的變化；ZHAO 等［12］對大長徑比下的水潤滑橡膠軸承進(jìn)行實驗研究并確定其動力特性［13］；GAO 等［14］用CFD［15］軟件對水潤滑徑向滑動軸承流體動力潤滑承載能力進(jìn)行分析，并提出了一種新型過渡弧軸承軸瓦，有利于提高水動力承載能力；DU 等［16］研究了不可壓縮層流靜壓軸承的動力學(xué)特性，將槽間流動連續(xù)方程從雷諾方程解耦，提高了計算效率；謝帆等［17］基于有限差分法計算了徑向滑動軸承油膜壓力分布；李超等［18］對考慮間隙影響的渦旋壓縮機(jī)轉(zhuǎn)子系統(tǒng)的動態(tài)特性進(jìn)行了研究；LI 等［19］采用窄軸承理論求解滑動軸承液膜的非定常雷諾方程并計算了動力學(xué)特征系數(shù)；成金貴等［20］運用平均雷諾方程和固體接觸理論建立了止推軸承接觸面間摩擦潤滑理論模型并進(jìn)行了試驗驗證；LI 等［21］推導(dǎo)了考慮五自由度運動時判別轉(zhuǎn)子穩(wěn)定性的臨界質(zhì)量快速計算公式。

綜上可知，現(xiàn)有研究均未考慮口環(huán)間隙水膜的動壓潤滑效應(yīng)，且尚無證據(jù)表明該效應(yīng)可以忽略。本文通過求解Reynolds 方程和轉(zhuǎn)子動力學(xué)特征方程，考慮口環(huán)間隙水膜動壓潤滑效應(yīng)的影響，研究了一體機(jī)轉(zhuǎn)子系統(tǒng)的臨界轉(zhuǎn)速及系統(tǒng)的臨界質(zhì)量，為保障海水淡化高壓泵與透平式能量回收一體機(jī)水潤滑轉(zhuǎn)子系統(tǒng)的穩(wěn)定運行提供參考。

1 模型及參數(shù)

本文研究對象為海水淡化高壓泵與透平式能量回收一體機(jī)中水潤滑轉(zhuǎn)子系統(tǒng)，其結(jié)構(gòu)如圖1所示。其轉(zhuǎn)子結(jié)構(gòu)左端為透平葉輪，右端為泵葉輪，中間部分為水潤滑軸承，泵葉輪進(jìn)口延伸段處的軸承為口環(huán)。一體機(jī)中轉(zhuǎn)子部件的主要結(jié)構(gòu)參數(shù)見表1。

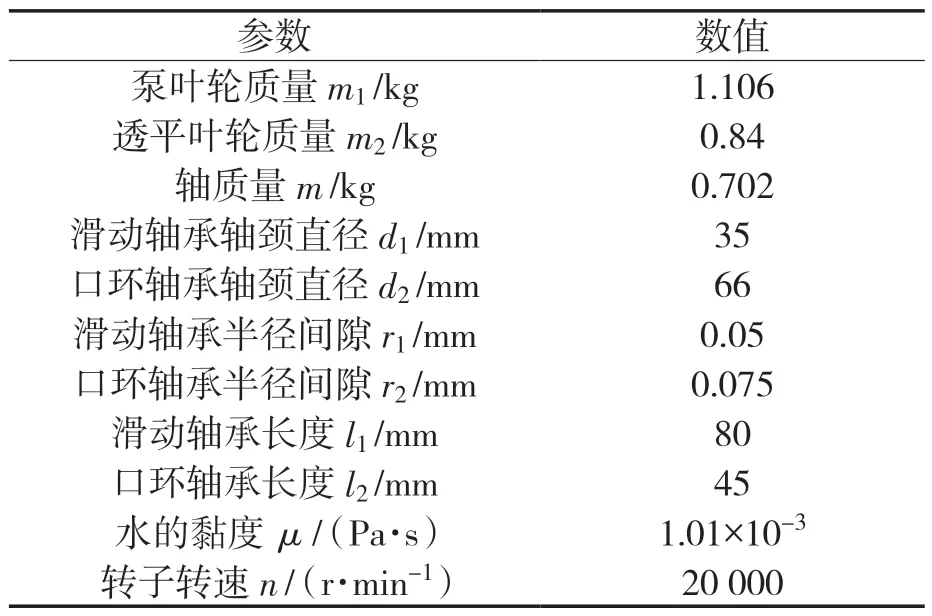
表1 水潤滑轉(zhuǎn)子系統(tǒng)結(jié)構(gòu)參數(shù)Tab.1 Structural parameters of water lubricated rotor system

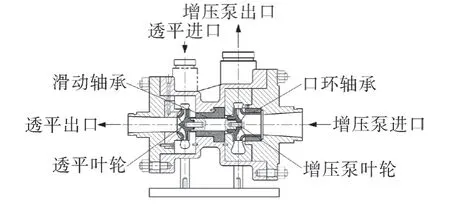
圖1 一體機(jī)水潤滑轉(zhuǎn)子系統(tǒng)結(jié)構(gòu)示意Fig.1 Structure diagram of water lubricated rotor system of all-in-one machine

2 水潤滑軸承動靜特性分析

在一體機(jī)中，轉(zhuǎn)子系統(tǒng)的動力學(xué)特性與軸承的支撐特性密切相關(guān)，水潤滑滑動軸承及口環(huán)軸承的動力特性計算與分析是整個轉(zhuǎn)子系統(tǒng)的核心。

2.1 水潤滑軸承靜特性計算

水潤滑軸承原理如圖2 所示，A點為沿y軸逆時針轉(zhuǎn)動φ后的位置，?為偏位角，θ=φ-?，c為半徑間隙，則水膜厚度h=c+ecosθ，e為偏心距。

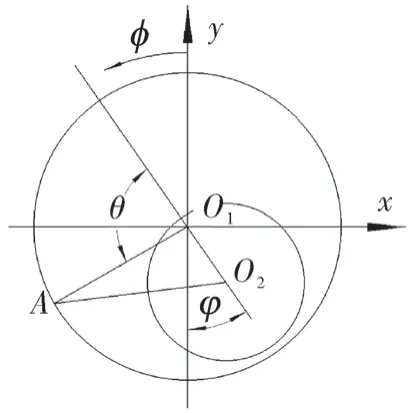
圖2 水潤滑軸承原理Fig.2 Schematic diagram of water-lubricated bearings

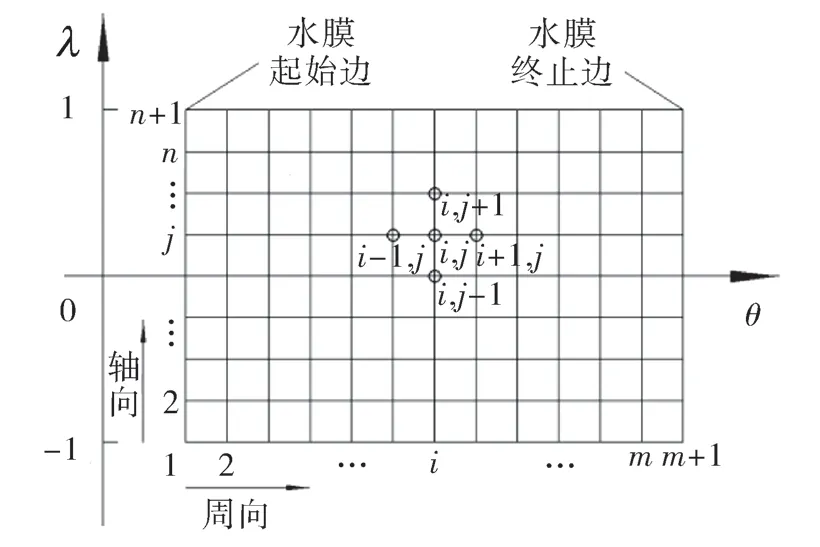
圖3 水膜網(wǎng)格劃分Fig.3 Water film meshing

水潤滑滑動軸承及口環(huán)軸承均屬于圓柱形流體動壓軸承，通過求解雷諾方程得到液膜壓力分布。無量綱化后的雷諾方程為：

式中，L為軸承長度；P為水膜壓力；R為軸頸半徑。

利用有限差分法計算水膜壓力，需對水膜進(jìn)行正交網(wǎng)格劃分，將水膜劃分成m×n的網(wǎng)格，如圖（i，j）處節(jié)點的壓力，且ΓΔPλ=2/n，Δθ=（θH2-θ1）/m，3 所示，每一個節(jié)點有對應(yīng)的坐標(biāo)，Pi，j表示坐標(biāo)為θ1為水膜起始角，θ2為水膜終止角。計算各節(jié)點的壓力求得壓力分布，將壓力分布以水膜表面進(jìn)行積分求得水膜承載力。

為了提高計算精度，采用半步長差分法，對水膜端面采用第一類邊界條件，即λ=±1，P=0；水膜周向上采用雷諾邊界條件，即起始邊固定，則有θ=0，P=0；水膜終止邊自由浮動，并取P=0，?P/?θ=0。采用超松弛迭代法計算各個節(jié)點的壓力值，初始化各個節(jié)點壓力值為P=0，代入雷諾邊界條件，求解得到壓力分布。

為求解水潤滑軸承動力特性系數(shù)，需要確定軸承偏心率及偏位角并求得水膜承載力。將水膜承載力分解為x方向和y方向，分別用Fx，F(xiàn)y表示，則有：

式中，F(xiàn)x，F(xiàn)y為無量綱水膜承載力；θ為水膜旋轉(zhuǎn)角，以x軸負(fù)方向為水膜角初始位置。

2.2 水潤滑軸承動特性計算

計算水潤滑軸承剛度阻尼動特性系數(shù)采用瞬態(tài)雷諾方程求解，對其無量綱化后可表示為［22-23］：

式中，ε'，ε?'為瞬時速度。

將式（4）依次對ε，?，ε'，ε?'求偏導(dǎo)得到擾動微分方程為：

由靜平衡位置及水膜壓力分布結(jié)合式（5）～（8）解得水膜擾動壓力，進(jìn)而求解水膜的剛度阻尼系數(shù)：

由上式解得滑動軸承及口環(huán)軸承動特性系數(shù)。

將式（9）（10）化為直角坐標(biāo)形式：

3 水潤滑轉(zhuǎn)子系統(tǒng)穩(wěn)定性分析

在一體機(jī)中，當(dāng)轉(zhuǎn)子受到擾動時能否保證系統(tǒng)平穩(wěn)運行與轉(zhuǎn)子的穩(wěn)定性密切相關(guān)。水潤滑轉(zhuǎn)子系統(tǒng)的穩(wěn)定性可由求解轉(zhuǎn)子動力學(xué)特征方程，通過其特征值實部判別，并通過求解轉(zhuǎn)子系統(tǒng)臨界質(zhì)量進(jìn)行穩(wěn)定性分析。

將一體機(jī)中轉(zhuǎn)子簡化為一維模型，由受力平衡、力矩平衡方程求得滑動軸承及口環(huán)軸承處所受到的壓力，受力分析如圖4 所示。其中G為軸質(zhì)量，G1，G2分別為透平葉輪質(zhì)量、泵葉輪質(zhì)量，F(xiàn)1，F(xiàn)2分別為滑動軸承、口環(huán)軸承所提供的承載力。

圖4 轉(zhuǎn)子受力分析Fig.4 Rotor stress analysis

列出平衡方程為：

求解得F1，F(xiàn)2后，進(jìn)而轉(zhuǎn)化為水膜承載力，分別解得滑動軸承剛度、阻尼矩陣K1，C1及口環(huán)軸承的剛度、阻尼矩陣K2，C2：

一體機(jī)轉(zhuǎn)子系統(tǒng)的動力學(xué)方程為：

式中，X為轉(zhuǎn)子的位置向量；M為質(zhì)量矩陣；C為阻尼矩陣；K為剛度矩陣；F為不平衡力。取F=0，則式（16）變?yōu)檗D(zhuǎn)子自由振動模型，改寫為：

因此可得到轉(zhuǎn)子系統(tǒng)的特征方程為：

式中，ξ為特征方程的根，為轉(zhuǎn)子質(zhì)量。

將式（18）展開可得：

式（21）的解即為系統(tǒng)的特征值，求得的特征值為兩對共軛的復(fù)根，即ξ=αi+im βi，其中αi（i=1，2，3，4）為特征值實部，im為虛數(shù)單位，β i為虛部。當(dāng)α i＜0 時，系統(tǒng)為穩(wěn)定運行狀態(tài)；當(dāng)α i=0 時，系統(tǒng)處于穩(wěn)定運行的臨界狀態(tài)；當(dāng)α i>0 時，系統(tǒng)處于不穩(wěn)定狀態(tài)，并求得系統(tǒng)臨界質(zhì)量。

綜上所述，求解水潤滑轉(zhuǎn)子系統(tǒng)的穩(wěn)定性流程如圖5 所示。

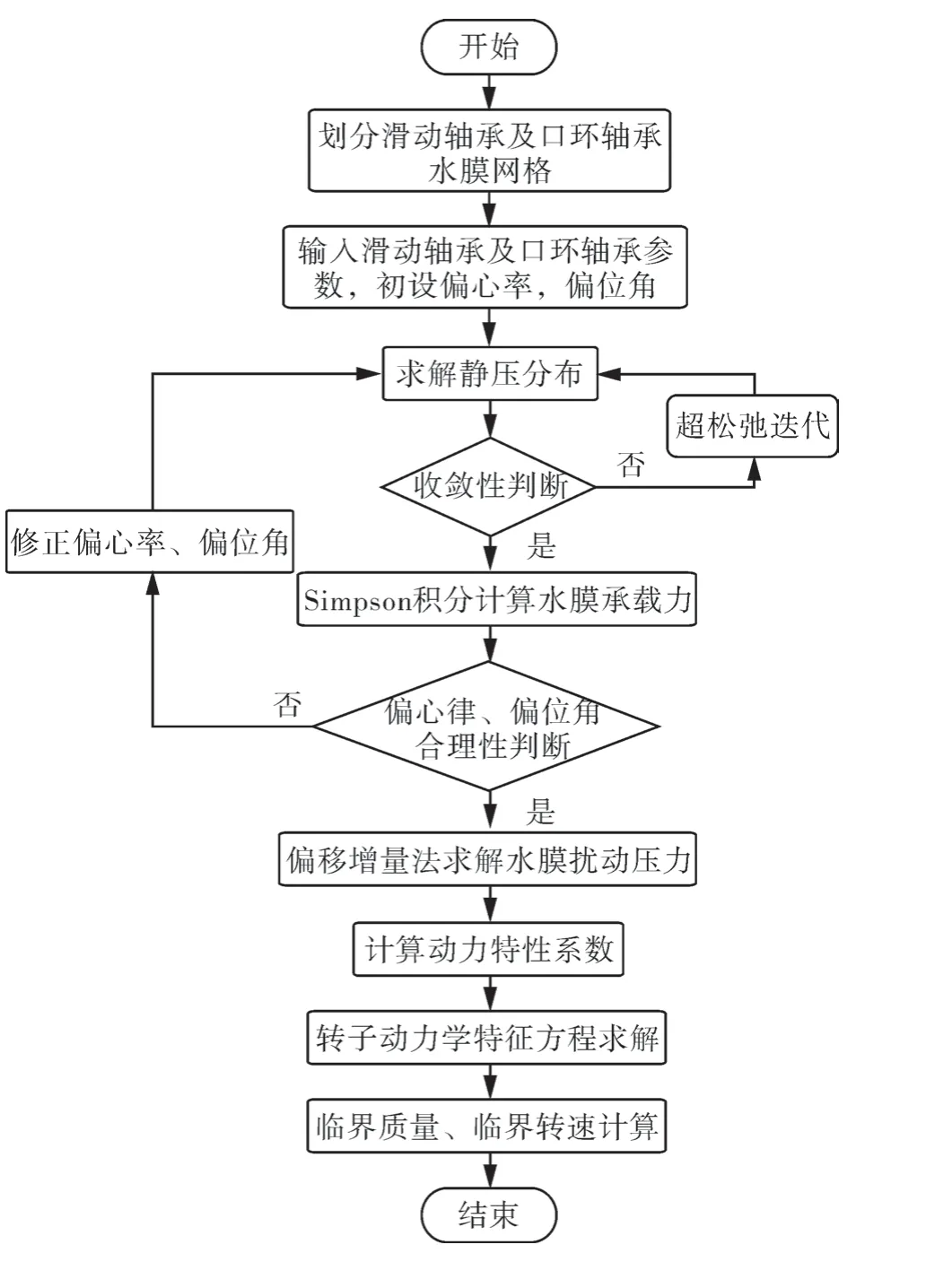
圖5 水潤滑轉(zhuǎn)子系統(tǒng)穩(wěn)定性程序框圖Fig.5 Water lubricated rotor system stability program block diagram

4 驗證

結(jié)合文獻(xiàn)［24］中模型參數(shù)，選取與文獻(xiàn)相同的計算模型參數(shù)，軸承直徑為30 cm，間隙比為0.002，寬徑比為0.8，轉(zhuǎn)速為3 000 r/min，載荷為65 000 N。圖6 示出MATLAB 計算結(jié)果與文獻(xiàn)中計算結(jié)果對比，其中主剛度系數(shù)Kxx，Kyy誤差為4%～4.4%，交叉剛度系數(shù)Kxy，Kyx誤差為0.4%～4.3%，主阻尼系數(shù)Cxx，Cyy誤差為3.3%～4.6%，交叉阻尼系數(shù)Cxy，Cyx誤差為4.1%～4.2%。考慮到計算過程中迭代算法和收斂準(zhǔn)則等差異，會導(dǎo)致存在一定的結(jié)果偏差，計算結(jié)果與文獻(xiàn)中的結(jié)果基本吻合，驗證了本文計算結(jié)果的可靠性。

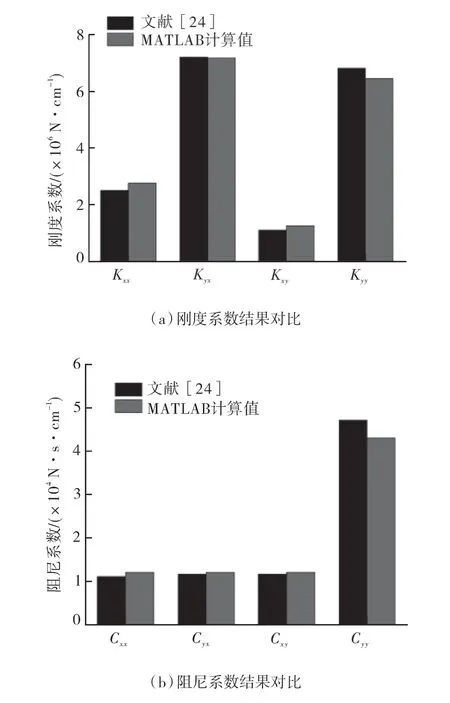
圖6 MATLAB 計算結(jié)果與文獻(xiàn)結(jié)果對比Fig.6 Comparison of MATLAB calculation results and literature results

5 結(jié)果分析

考慮口環(huán)軸承前、后，軸承水膜壓力分布如圖7 所示，對比可知滑動軸承處水膜壓力約減小了40%。當(dāng)轉(zhuǎn)子系統(tǒng)考慮口環(huán)間隙水膜所產(chǎn)生的流體動壓潤滑效應(yīng)后，口環(huán)軸承會承擔(dān)一部分支撐作用。由于在一定的載荷下，相應(yīng)的水膜提供的承載力也是一定的，因此滑動軸承處水膜壓力的減小量近似于口環(huán)軸承水膜壓力的增量。

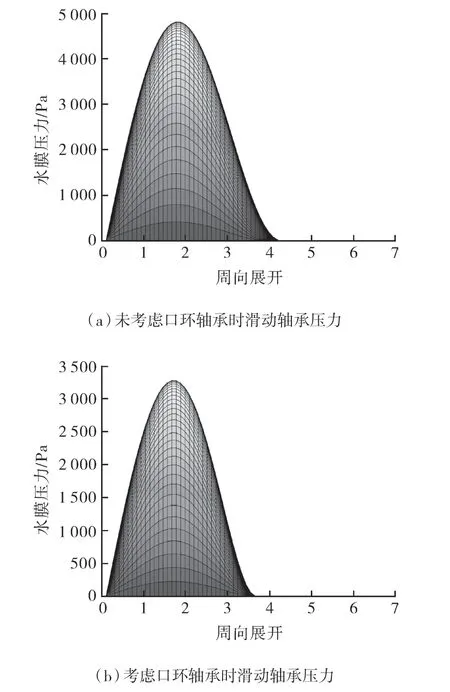
圖7 水膜壓力分布Fig.7 Water film pressure distribution

當(dāng)一體機(jī)轉(zhuǎn)子系統(tǒng)考慮口環(huán)軸承后，滑動軸承及口環(huán)軸承的剛度系數(shù)隨著轉(zhuǎn)速變化規(guī)律如圖8 所示。兩軸承的主剛度系數(shù)各自近似相等，即K1xx=K1yy，K2xx=K2yy，隨著轉(zhuǎn)速增加，滑動軸承主剛度呈明顯線性遞增的趨勢，而口環(huán)軸承僅小幅增加。滑動軸承與口環(huán)軸承的交叉剛度系數(shù)均呈x軸對稱分布，即K1xy=-K1yx，K2xy=-K2yx，且滑動軸承的交叉剛度約為口環(huán)軸承的5 倍。隨著轉(zhuǎn)速增加，兩軸承的交叉剛度系數(shù)均增大。

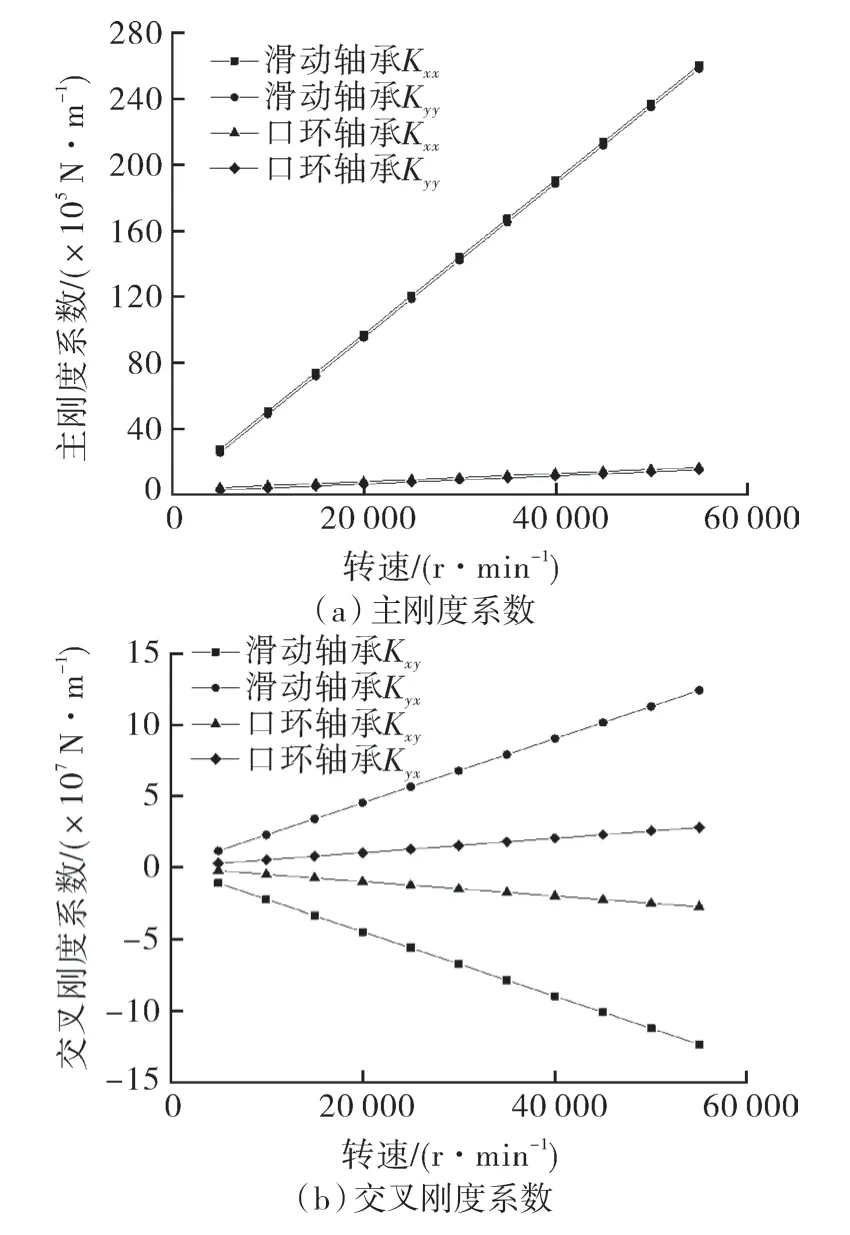
圖8 剛度系數(shù)與轉(zhuǎn)速的關(guān)系Fig.8 The relationship between stiffness coefficient and rotational speed

當(dāng)一體機(jī)轉(zhuǎn)子系統(tǒng)考慮口環(huán)軸承后，滑動軸承及口環(huán)軸承的阻尼系數(shù)變化曲線如圖9 所示。隨著轉(zhuǎn)速的增加，滑動軸承及口環(huán)軸承主阻尼系數(shù)無明顯變化。對于交叉剛度系數(shù)而言，當(dāng)轉(zhuǎn)速＜15 000 r/min 時，系數(shù)變化較為明顯且呈減小趨勢；當(dāng)轉(zhuǎn)速＞15 000 r/min 時，系數(shù)趨于穩(wěn)定不再變化，且C1xy=C1yx，C2xy=C2yx。

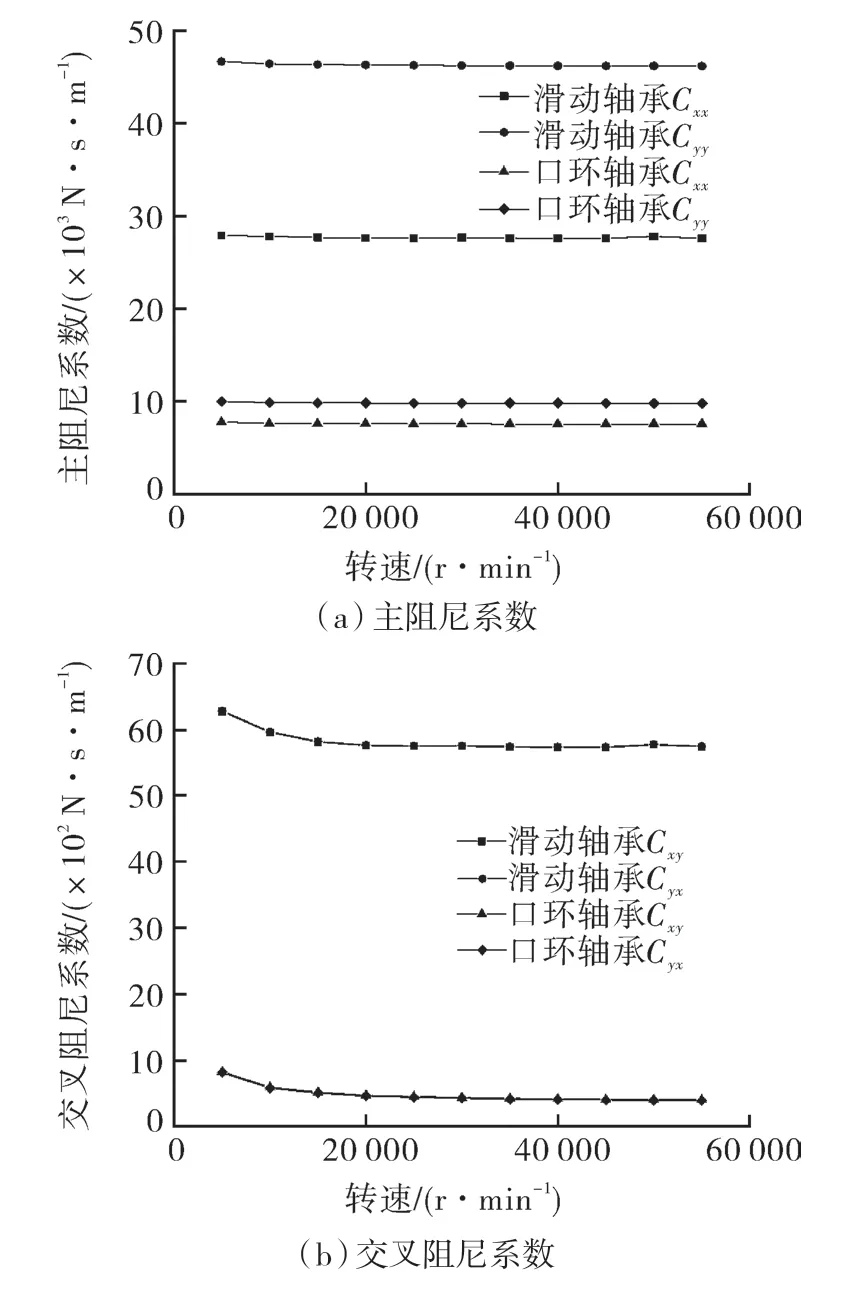
圖9 阻尼系數(shù)與轉(zhuǎn)速的關(guān)系Fig.9 The relation between damping coefficient and rotational speed

考慮口環(huán)軸承前、后的動力特性系數(shù)分別為A，B，則動力特性系數(shù)變化率表示為：（B-A）/A×100%，則其變化率如圖10 所示。考慮口環(huán)軸承后，系統(tǒng)動力特性系數(shù)均有所增加，系統(tǒng)交叉剛度系數(shù)及主阻尼系數(shù)增加量超過20%，主剛度系數(shù)和交叉阻尼系數(shù)增加5%左右。因此一體機(jī)轉(zhuǎn)子系統(tǒng)中口環(huán)軸承的存在有利于水潤滑軸承承載特性的提升。

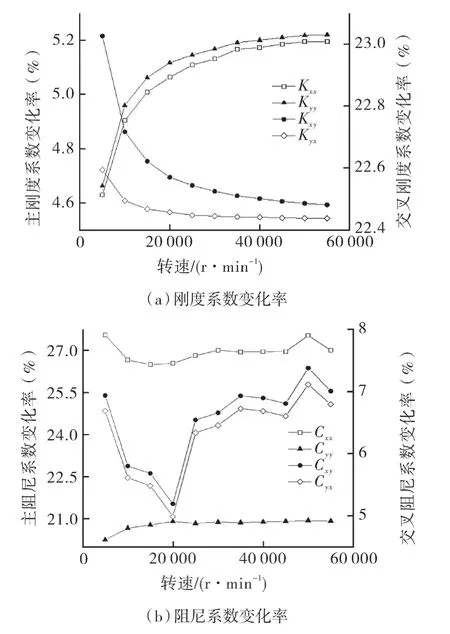
圖10 動特性系數(shù)變化率Fig.10 Rate of change of dynamic characteristic coefficient

添加口環(huán)軸承后特征值變化曲線如圖11 所示，臨界質(zhì)量變化曲線如圖12 所示。

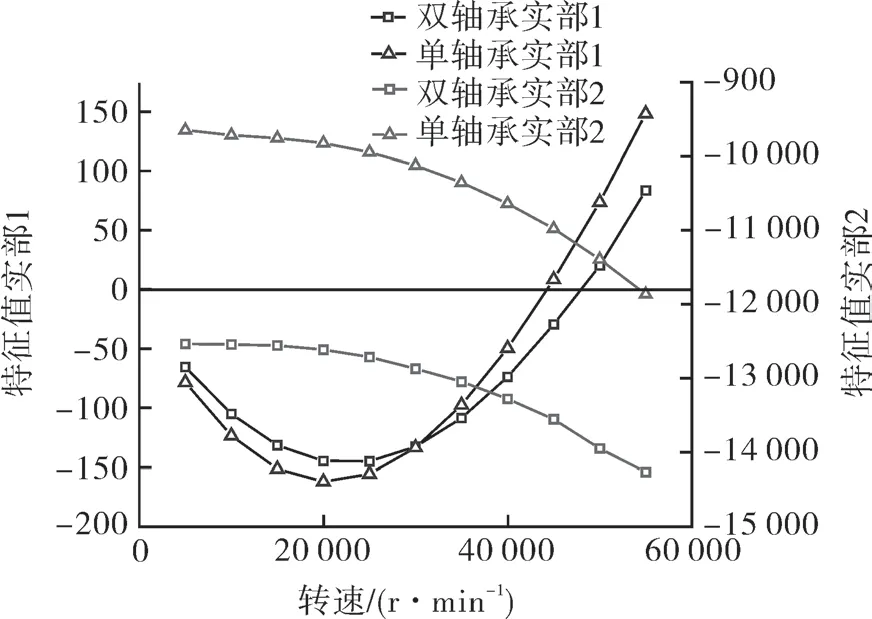
圖11 特征值變化曲線Fig.11 Eigenvalue change curve

特征方程的解為2 個共軛負(fù)根，且有2 個實部，隨著轉(zhuǎn)速的升高實部1 呈現(xiàn)先減小后增大的趨勢，而實部2 單調(diào)遞減且恒為負(fù)值。考慮口環(huán)軸承后，實部1 有所增加但上升趨勢減緩，故而臨界穩(wěn)定狀態(tài)時的轉(zhuǎn)速增加。隨著轉(zhuǎn)速增加，系統(tǒng)的臨界質(zhì)量逐漸減小，在一體機(jī)工作轉(zhuǎn)速下，考慮口環(huán)軸承支撐后系統(tǒng)的臨界質(zhì)量將提升8.4%左右。因此未考慮口環(huán)軸承將導(dǎo)致系統(tǒng)臨界轉(zhuǎn)速和臨界質(zhì)量的計算產(chǎn)生誤差，從而影響水潤滑轉(zhuǎn)子系統(tǒng)穩(wěn)定性設(shè)計的準(zhǔn)確性。

不同長徑比下水潤滑轉(zhuǎn)子系統(tǒng)臨界質(zhì)量變化如圖13 所示，長徑比的增加使得系統(tǒng)的臨界質(zhì)量增加，且在低轉(zhuǎn)速下臨界質(zhì)量受長徑比的影響較為明顯，這是由于軸承的剛度增加，承載性能有所提升，增大軸承的長徑比有利于提高系統(tǒng)穩(wěn)定性。

圖13 不同長徑比的臨界質(zhì)量Fig.13 Critical mass of different length diameter ratio

不同半徑間隙下的水潤滑轉(zhuǎn)子系統(tǒng)臨界質(zhì)量變化如圖14 所示，隨著軸承半徑間隙的增加，系統(tǒng)的臨界質(zhì)量逐漸降低，軸承的承載能力下降導(dǎo)致系統(tǒng)在高轉(zhuǎn)速下運行不穩(wěn)定，因此采用減小半徑間隙的方法來提升系統(tǒng)的臨界質(zhì)量，且臨界質(zhì)量隨半徑間隙的降低呈現(xiàn)非線性增加，半徑間隙越小，臨界質(zhì)量的增量越大。

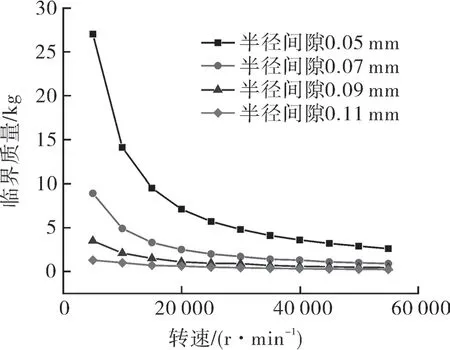
圖14 不同半徑間隙的臨界質(zhì)量Fig.14 Critical mass of gap with different radius

6 結(jié)論

（1）當(dāng)未考慮口環(huán)間隙水膜時，滑動軸承水膜將會承受更高的壓力；而考慮口環(huán)軸承則降低了滑動軸承的偏心率，有利于提高系統(tǒng)的穩(wěn)定性。

（2）當(dāng)未考慮口環(huán)軸承時，水潤滑轉(zhuǎn)子系統(tǒng)動特性系數(shù)的求解準(zhǔn)確性將會降低；考慮口環(huán)軸承后，其動特性系數(shù)均有所增加，其中交叉剛度系數(shù)及主阻尼系數(shù)增幅超過20%，主剛度系數(shù)與交叉阻尼系數(shù)增加約為5%，且隨轉(zhuǎn)速的增加趨于穩(wěn)定。

（3）當(dāng)未考慮口環(huán)軸承時系統(tǒng)的臨界轉(zhuǎn)速和臨界質(zhì)量的求解結(jié)果存在一定偏差，均比考慮口環(huán)軸承時有所減小，其中系統(tǒng)的臨界轉(zhuǎn)速減小7%，臨界質(zhì)量減小8.4%。因此，考慮口環(huán)間隙水膜的動壓潤滑效應(yīng)可提高一體機(jī)水潤滑轉(zhuǎn)子系統(tǒng)的穩(wěn)定性。

（4）適當(dāng)增加軸承的長徑比、減小半徑間隙可以有效提高其承載性能和臨界質(zhì)量，有助于增強(qiáng)其轉(zhuǎn)子系統(tǒng)的穩(wěn)定性。