尺寸偏差下的車身含膠滾邊滾輪的位姿補償

李默之 朱文峰 王順超

摘要 ： 針對鋁合金車身更嚴格的外觀精度要求，提出一種面向車身尺寸偏差的滾輪位姿補償方法。首先對尺寸偏差區間與胎模邊線進行等距離散，得到尺寸偏差矩陣；然后基于Frenet標架與齊次坐標變換將尺寸偏差映射為滾輪位姿，得到滾輪位姿偏差矩陣；最后將滾輪位姿補償量轉化為滾輪位姿偏差矩陣行編號的調整量，得到補償后的滾輪位姿。其中，滾輪位姿偏差矩陣由胎模曲面/曲線方程、滾輪傾角，以及FEM-SPH有限元仿真獲得的尺寸偏差與TCP-RTP值的量化模型決定。實驗結果表明，滾輪位姿補償后的車身尺寸偏差平均值由0.32 mm降至0.14 mm。

關鍵詞 ：滾壓成形；偏差；工藝補償；折邊膠

中圖分類號 ：U463.82

DOI：10.3969/j.issn.1004-132X.2024.02.021

開放科學（資源服務）標識碼（OSID）：

Roller Pose Compensation in Automotive Body Roll-hemming Forming

Process with Adhesive for Dimensional Deviation

LI Mozhi ZHU Wenfeng WANG Shunchao

School of Mechanical Engineering，Tongji University，Shanghai，201804

Abstract ： In order to meet the stricter requirements for appearance accuracy of aluminum alloy automotive bodies， a roller pose compensation method was proposed for the dimensional deviation of automotive bodies. The dimensional deviation matrix was obtained by equidistant discretization of the dimensional deviation interval and the die edge. Based on the Frenet scale frame and Cartesian coordinate transformation， the dimensional deviation was mapped to the roller pose， and the deviation matrix of roller pose was obtained. The roller pose compensation amount was converted into the adjustment amount of the row number of the deviation matrix of roller pose， and the compensated roller pose was obtained. Among them， the deviation matrix of roller pose was determined by the surface/curve equation of die， the roller angle and the quantization model of dimensional deviation and the value of tool center point-robot target point（TCP-RTP）. The quantization model of dimensional deviation and the value of TCP-RTP was obtained by finite element simulation of finite element method-smoothed particle hydrodynamics. The results show that the average value of the dimensional deviation is reduced from 0.32mm to 0.14mm after the roller pose compensation.

Key words ： roller forming； deviation； technological compensation； hemming adhesive

0 引言

鋁合金車身是影響車輛外觀的重要部件，有著極高的外觀與裝配精度要求，部分整車廠對鋁合金車身的外觀與裝配精度要求達到0.01mm。機器人含膠滾邊即在車身內外板間涂覆折邊膠，利用工業機器人驅動滾輪，按照預定的位姿與軌跡實現車身內外板的連接，是車身制造的重要工藝 ?［1-3］ 。車身尺寸偏差不可避免，傳統滾邊工藝中，滾輪位姿與軌跡無法根據車身尺寸偏差調整。滾邊工藝中，內外板的劇烈擠壓會導致折邊膠（高黏度的非牛頓流體）產生壓黏效應 ?［4］ 。上述兩個因素導致現有的滾邊方法難以使車身外觀與裝配精度進一步提高。因此，考慮車身尺寸偏差的含膠滾邊滾輪的位姿補償研究具有良好的理論意義與工程應用背景。

在折邊膠與滾邊工藝參數對車身尺寸偏差影響研究中，LIN等 ?［5］ 研究了鋁合金薄板在包邊成形工藝中的成形性能，分析了包邊工藝參數對成形性能的影響。GRGEN ?［6］ 研究了板材厚度、彎曲角度、滾輪直徑等工藝參數對曲面零件縮進脹出、變形、波浪起皺和滾邊力的影響。李建軍等 ?［7］ 使用FEM-SPH（finite element method-smoothed particle hydrodynamics）方法建立了車身含膠滾邊工藝仿真模型，研究了折邊膠對滾邊工藝成形質量的影響。滾輪軌跡求解的研究中，文獻［8-10］研究了車身門蓋件曲面/曲邊的含膠滾邊工藝，通過微分幾何計算出理論滾輪位姿與軌跡，并對滾邊過程進行了數值仿真。軌跡規劃與控制研究中，文獻［11-13］研究了機器人軌跡精度對噴涂、除銹等領域的加工誤差的影響，并提出了提高軌跡精度的控制方法。綜上所述，目前對車身含膠滾邊工藝的研究主要集中在成形質量影響因素的分析及滾邊精確軌跡的求解，缺乏對縮減車身尺寸偏差的研究。同時，滾輪位姿體現了滾輪與胎模間的相對位置關系，決定著車身尺寸偏差的大小。因此，需要建立面向尺寸偏差的滾輪位姿補償模型與方法。

為此，本文基于FEM-SPH方法對含膠滾邊工藝進行數值仿真，定量分析滾邊工藝參數TCP-RTP（tool center point-robot target point）值對車身尺寸偏差的影響，建立尺寸偏差與TCP-RTP值的量化模型；以尺寸偏差與TCP-RTP值的量化模型、胎模曲面/曲線方程、滾輪傾角為輸入量，基于Frenet標架與齊次坐標變換理論，建立表征車身尺寸偏差與滾輪位姿對應關系的滾輪位姿偏差矩陣模型，并根據尺寸偏差確定滾輪位姿補償量；搭建機器人滾邊實驗平臺來驗證尺寸偏差與TCP-RTP值的量化模型的準確性，以及滾輪位姿補償方法對縮減車身尺寸偏差的有效性。

1 面向車身尺寸偏差的滾輪位姿補償 方法

1.1 車身尺寸偏差與TCP-RTP值的定義

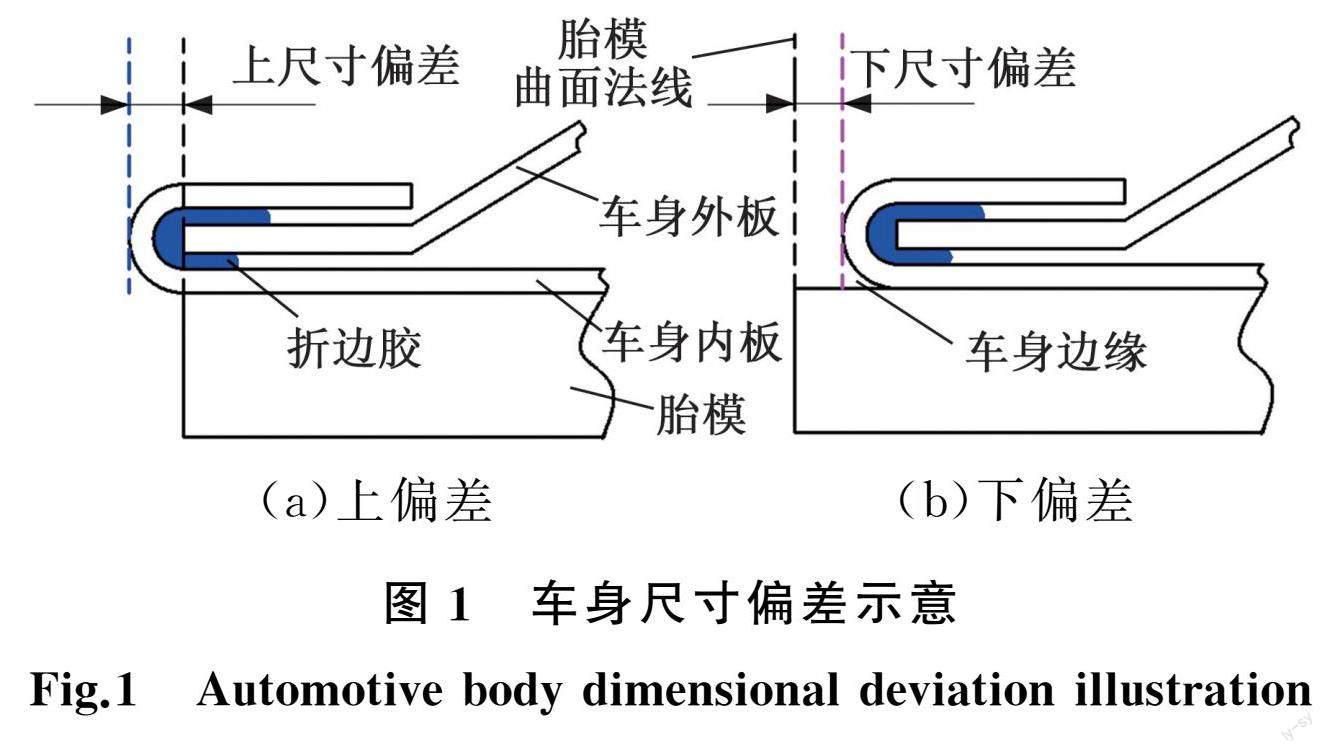
理想狀況下，車身邊緣與胎模邊線在胎模曲面的法向重合。車身邊緣偏離胎模曲面法線時，車身將產生尺寸偏差。車身邊緣向外偏離胎模曲面法線造成的尺寸偏差為上偏差， 并規定偏差值為正；車身邊緣向內偏離胎模曲面法線造成的尺寸偏差為下偏差，并規定偏差值為負，如圖1所示。

滾輪母線距胎模邊線的垂直距離 l 稱為TCP-RTP值，其中，機器人的工具中心點（tool center point，TCP）位于滾輪母線上，機器人目標點（robot target point，RTP）位于胎模邊線上，將滾輪軸線與胎模曲面法線的夾角θ定義為滾輪傾角，如圖2所示。RTP、TCP-RTP值與滾輪傾角共同決定了滾輪與胎模間的相對位置關系。

1.2 滾輪位姿補償方法

滾輪是機器人含膠滾邊工藝中的重要執行工具，在滾輪位姿中引入車身尺寸偏差是確定滾輪位姿補償量的前提。首先，將車身尺寸偏差區間與胎模邊線進行等距離散，得到車身尺寸偏差矩陣 δ 。圖3中，i為尺寸偏差離散編號，j為 RTP 離散編號，δ′為相鄰離散尺寸偏差的間距。其次，求解車身尺寸偏差矩陣中所有元素所對應的滾輪位姿，得到滾輪位姿偏差矩陣 G 。

車身尺寸偏差與滾輪位姿偏差矩陣的對應關系如圖4所示。

此時，滾輪位姿偏差矩陣 G 的行向量表示某一離散尺寸偏差下的滾輪軌跡，列向量表示某一離散機器人目標點處各離散尺寸偏差所對應的滾輪位姿。

基于滾輪位姿偏差矩陣給出滾輪位姿的補償方法：①由于滾輪位姿偏差矩陣與尺寸偏差矩陣中的元素相互對應，因此可通過尺寸偏差確定當前滾輪的位姿；②再將滾輪位姿的補償量轉換為滾輪位姿偏差矩陣行編號的調整量，從而得到補償后的滾輪位姿。

如圖5所示，當滾輪運行到點j處時，對點 j-1 處的尺寸偏差δ ?i，j-1 進行測量。由于尺寸偏差矩陣與滾輪位姿偏差矩陣的元素相互對應，故可得到j-1處的滾輪位姿G ?i，j-1 。

尺寸偏差區間是等距離散的，根據點j-1處的尺寸偏差δ ?i，j-1 與相鄰離散尺寸偏差的間距δ′可以獲得滾輪位姿偏差矩陣行編號的調整量 Δ i：

Δ i=－ δ ?i，j－1 ?δ′ ??（1）

最終，在點j+1處輸入補償后的滾輪位姿G ?i+ Δ i，j+1 。

2 滾輪位姿偏差矩陣的推導

滾輪位姿偏差矩陣是滾輪位姿補償的依據，本節將對滾輪位姿偏差矩陣進行數學建模。

2.1 基于Frenet標架的機器人目標點位姿

給定胎模曲面方程 S = S （u，v），胎模邊緣曲線方程 C = C （u（t），v（t））= C （t）。O點是胎模邊線上任意 RTP ，如圖6所示。機器人目標點的位姿 B （t）由機器人目標點的姿態與位置共同組成。基于 Frenet 標架理論可得機器人目標點的姿態：

α （t）= ?C ′（t） | C ′（t）|

γ （t）= ?n （t） | n （t）|

β （t）= γ （t）× α （t）

n （t）=［ S ?u（u，v）× S ?v（u，v）］| ?u=u（t），v=v（t） ???（2）

式中， C ′（t）為曲線 C 的切向量； n （t）為曲面 S 的法向量； α （t）為曲線 C 的單位切向量； γ （t）為曲面 S 的單位法向量； S ??u （u，v）、 S ??v （u，v）分別為曲面 S 在（u（t），v（t））點對參數u、v的偏導數。

任意 RTP 的姿態 R （t）可表示為

R （t）=（α（t），β（t），γ（t）） ?（3）

RTP 的位置為

P （t）=（c x（t），c y（t），c z（t）） ?T ??（4）

式中，c x（t）、c y（t）、c z（t）分別為曲線 C 在X、Y、Z方向的參數方程。

機器人目標點的位姿 B （t）可表示為

B （t）= ??R （t） ?P （t） 0 ?1 ???（5）

2.2 滾輪位姿偏差矩陣模型

滾輪位姿 G 由胎模曲面法線與滾輪軸線的交點O 1的位置與姿態組成，由機器人目標點位姿 B （t）通過齊次坐標變換得到，如圖7所示。

如圖8所示，機器人目標點首先由O點平移至O 1點，平移矢量為

D （θ，l）=（0，0， l+r ?cos ?θ ） ?T ??（6）

式中，r為滾輪半徑。

接著，機器人目標點以O 1點為原點，繞平移后O 1點的單位向量 α ′（t）逆時針旋轉90 ° -θ，旋轉矩陣 R ?α（θ）可表示為

R ?α（θ）= ?1 0 0 0 ?sin ?θ ?cos ?θ 0 - cos ?θ ?sin θ ???（7）

含膠滾邊過程中， TCP-RTP 值影響車身尺寸偏差，同時，車身尺寸偏差也會反映 TCP-RTP 值的大小。車身尺寸偏差δ與 TCP-RTP 值l的量化模型為

l=f（δ） ?（8）

由式（6）～式（8）可得機器人目標點位姿 B （t）與滾輪位姿 G 間的齊次坐標變換矩陣：

T （θ，δ）= ??R ?α（θ） ?D （θ，δ） 0 ?1 ???（9）

由式（5）、式（9）可得滾輪位姿：

G = T （θ， δ） B （t） ?（10）

車身尺寸偏差區間與胎模邊線等距離散（前者離散成一個個尺寸偏差，后者離散成一個個機器人目標點，如圖4所示）后，可得滾輪位姿矩陣：

G ?ij =T（θ， δ ?ij ）B（t j）=T ?ij B j ?（11）

3 滾輪位姿偏差矩陣求解

3.1 車身尺寸偏差與TCP-RTP值的量化模型

車身含膠滾邊過程中，胎模曲面、曲線方程與滾輪傾角都已確定，此時，得到車身尺寸偏差與TCP-RTP值的量化模型，便可求解滾輪位姿偏差矩陣。改變TCP-RTP值，進行多組車身含膠滾邊有限元仿真并對尺寸偏差進行統計，最終獲得車身尺寸偏差與TCP-RTP值的量化模型。

鋁合金車門是典型的車身部件，因此選擇鋁合金車門窗框段作為仿真對象。滾輪傾角為90°，胎模的曲面、曲線方程為

S （u，v）=（u，v，0）

C （t）=（t，－5.666 57×10 ?－6 t 3－

2.523 32×10 ?－4 t 2+3.95×10 ?－3 t，0） ??（12）

u∈［0，150］ mm ??v∈［-100，100］ mm

t∈［0，150］ mm

光滑粒子流體動力學（smoothed particle hydrodynamics，SPH） 法是一種無網格的有限元仿真方法。相比于傳統的Lagrange法，SPH法更適合求解折邊膠在板材擠壓作用下的非線性與大變形問題。因此，采用FEM-SPH法對鋁合金車門窗框段含膠滾邊工藝進行有限元仿真 ?［7］ 。車門窗框段外板采用型號AA6061-T4的鋁合金，采用FEM劃分網格；采用SPH法將折邊膠（陶氏BETAMATETM）設置為光滑流體動力學粒子；滾輪、胎模與內板使用剛度較大的不銹鋼， 三者的變形可忽略，因此設置為剛體。車身含膠滾邊仿真步驟如圖9所示。模型的主要參數如表1所示。

為折邊膠保留必要的流道，將TCP-RTP值的起始值設為2.9 mm，每隔0.1 mm進行一組仿真。統計離散機器人目標點處的尺寸偏差，如圖10所示，可以看出，隨著TCP-RTP值的增大，車門窗框段的尺寸偏差逐漸從上偏差過渡到下偏差。同時，將 l 為3.4 mm時的最小下尺寸偏差 與 l 為2.9 mm時的最大上尺寸偏差作為車門窗框段的尺寸偏差區間的左右端點。

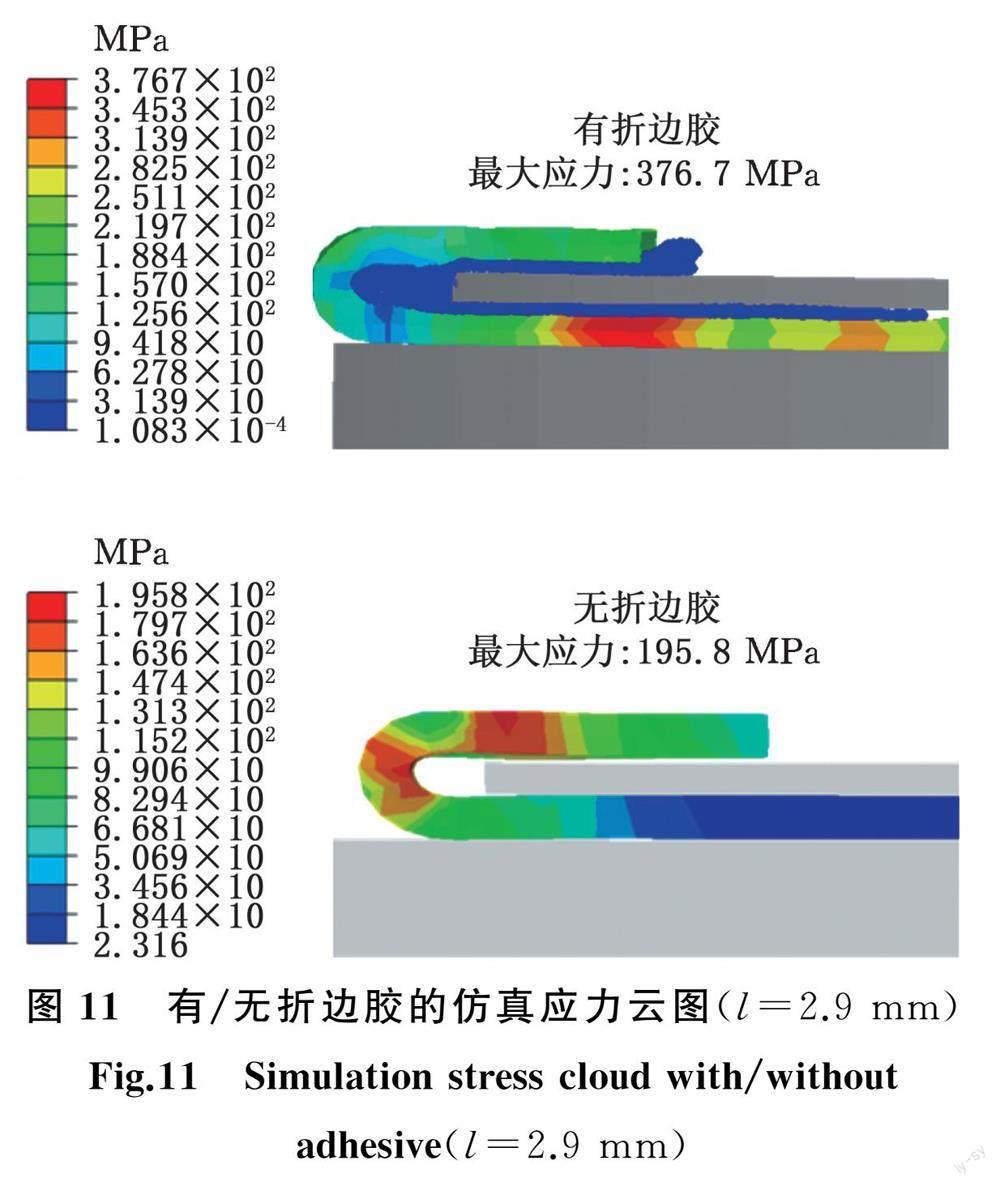
相同TCP-RTP下，有/無折邊膠的仿真結果如圖11所示，可以看出，有折邊膠車身的最大應力與尺寸偏差都明顯較大，說明折邊膠的壓黏效應對車身尺寸偏差的影響不可忽略。

為建立TCP-RTP值與尺寸偏差間的量化模型，在仿真模型上均勻取5個采樣點，統計各采樣點處不同TCP-RTP值對應的尺寸偏差。將各采樣點處的尺寸偏差 δ 與TCP-RTP值進行直線擬合，直線擬合的決定系數 R ?2均在0.99附近，如圖12所示。因此，車門窗框段的尺寸偏差與TCP-RTP的量化模型可表示為

l ?ij =f（δ ?ij ）=k jδ ?ij +b j ?（13）

式中，k j、b j為線性擬合參數。

3.2 滾輪位姿偏差矩陣求解軟件

滾輪位姿偏差矩陣求解涉及大量復雜的矩陣與微分幾何運算，因此依據滾輪位姿偏差矩陣建模流程，開發了滾輪位姿偏差矩陣計算軟件工具，實現滾輪位姿偏差矩陣快速準確的求解。圖13所示為滾輪位姿偏差矩陣計算軟件框架。

使用MATLAB語言進行尺寸偏差與TCP-RTP值仿真數據的線性擬合、胎模曲面/曲線的Frenet標架計算、齊次坐標變換矩陣的構建，最終實現滾輪位姿偏差矩陣的解算。使用AppDesigner創建軟件界面，將輸入量與輸出量分塊布置，便于人機交互。圖14所示為滾輪位姿偏差矩陣計算軟件工具界面。

當前研究側重于分析滾輪位姿補償對縮減車身尺寸偏差的有效性，僅以車身局部輪廓為樣本進行含膠滾邊的有限元仿真，仿真結果的數據規模較小。因此，使用軟件工具前需要采用手工方式將尺寸偏差與TCP-RTP值的有限元仿真數據保存為EXCEL文件。使用軟件工具時，有限元仿真數據的EXCEL文件、滾輪傾角、離散數目與胎模曲面/曲線方程為輸入量。運行軟件工具后，軟件工具輸出相應的滾輪位姿偏差矩陣。實際工業應用中，可在現有滾輪位姿偏差矩陣求解算法的基礎上實現更多軟件功能的擴充。

4 含膠滾邊滾輪位姿補償實驗

為驗證上述滾輪位姿補償方法的有效性，對車身窗框段進行滾輪位姿補償實驗，如圖15所示，滾邊機器人為庫卡KR600。尺寸偏差由固定在滾輪直桿上的高清攝像機檢測，精度為0.02 mm。補償后的滾輪位姿通過示教盤輸入滾邊機器人。

將采用滾輪位姿補償方法的實驗樣件稱為補償件，將不采用滾輪位姿補償方法的實驗樣件稱為對照件。為直觀比較補償件與對照件的尺寸偏差，將胎模邊緣涂紅，如圖16所示。

使用游標卡尺（精度為0.01 mm）對尺寸偏差進行測量，測量結果如圖17所示。

設置對照件的TCP-RTP值為3.4 mm，對照件的尺寸偏差與相同TCP-RTP值下有限元仿真得到的尺寸偏差吻合，證明了仿真結果的準確性。

補償件的尺寸偏差決定了滾輪位姿的補償量。離散機器人目標點編號為1～6時，補償件的初始尺寸偏差絕對值較大，滾輪位姿具有較大的補償量，因此這一階段補償件的尺寸偏差絕對值迅速縮減。離散機器人目標點編號為6～13時，補償件的尺寸偏差絕對值縮減到了0.2 mm以內，滾輪位姿的補償量減小，這一階段補償件的尺寸偏差絕對值振蕩減小。離散機器人目標點編號為13～21時，補償件的尺寸偏差絕對值進一步減小，滾輪位姿的補償量也進一步減小，補償件的尺寸偏差絕對值最終穩定在了0.1 mm以內。

對照件尺寸偏差絕對值的平均值為0.32 mm， 補充件尺寸偏差絕對值的平均值為0.14 mm，說明本文提出的滾輪位姿補償方法有效。

5 結論

（1）滾輪位姿偏差矩陣是滾輪位姿補償的依據與前提。

（2）滾輪位姿偏差矩陣由胎模曲面/曲線方程、滾輪傾角、尺寸偏差與TCP-RTP值的量化模型決定。

（3）車門窗框段尺寸偏差與TCP-RTP值的量化模型可用直線擬合，且隨著TCP-RTP值的增大，車門窗框段尺寸偏差逐步由上偏差過渡到下偏差。

（4）實驗表明，車門窗框段尺寸偏差的實驗值與FEM-SPH仿真值吻合；滾輪位姿補償后，車門窗框段尺寸偏差平均數值由0.32 mm降至0.14 mm。

參考文獻 ：

［1］ ?LIMON-LEYVA ?P， BALVANTN A， DIOSDADO-DE-LA-PEA J， et al. Parametric Optimization of Roll-hemming Process in Oblique Planes with Linear and Non-linear Trajectories［J］. Journal of Manufacturing Processes，2020， 50：123-131.

［2］ ?YUVARAJ ?K， VIGNESHWARAN S. Investigation on Spot Welding and Roller Hemming by Robots［J］. Materials Today：Proceedings，2021， 45：1075-1080.

［3］ ?沈健. 白車身四門兩蓋滾邊技術機器人程序及工藝優化方法研究［J］. 上海交通大學學報，2016，50（S1）：19-22.

SHEN Jian. The Research on Robot Program and Process Optimization Methods of Roller Hemming Technology of Body-in-white Anbauteile［J］. Journal of Shanghai Jiao Tong University， 2016， 50（S1）：19-22.

［4］ ?INGELSTEN ?S， MARK A， KDR R， et al. Simulation of Viscoelastic Squeeze Flows for Adhesive Joining Applications［J］. Journal of Non-Newtonian Fluid Mechanics， 2022， 300：104722.

［5］ ?LIN ?G， HU S J， CAI W. Evaluation of Formability in Ending/Hemming of Aluminum Alloys Using Plane-strain Tensile Tests［J］. Journal of Manufacturing Science and Engineering，2009，131（5）：051009.

［6］ ?GRGEN ?S. Numerical Modeling of Roller Hemming Operation on a Straight Edge Part［J］. Journal of the Brazilian Society of Mechanical Sciences and Engineering，2019，41（11）：1-7.

［7］ ?李建軍，朱文峰.基于SPH的平面曲線鋁合金薄板滾壓成形數值仿真與試驗研究［J］. 機械工程學報，2020， 56（24）：61-71.

LI Jianjun， ZHU Wenfeng. Numerical Simulation and Experiment of Roller Hemming-compression with Flat Surface-curved Edge Aluminum Alloy Sheet Based on SPH［J］. Journal of Mechanical Engineering， 2020，56（24）：61-71.

［8］ ?WANG ?S， ZHU W， LI M. Differential Geometry Modeling and Application of Roller Pose and Trajectory of Robot Roller Hemming for Complex Curved Surface-curved Edge Panels［J］. Robotics and Computer-Integrated Manufacturing， 2023， 83：102565.

［9］ ?NEUGEBAUER ?R， DROSSEL W， RSSINGER M， et al. Roller Hemming Simulation：State of the Art and Application Limits［J］. Key Engineering Materials， 2014， 611：1062-1070.

［10］ ?LE MAOT ?N， MANACH P， THUILLIER S. Influence of Prestrain on the Numerical Simulation of the Roller Hemming Process［J］. Journal of Materials Processing Technology， 2012， 212（2）：450-457.

［11］ ?LI ?R， DING N， ZHAO Y， et al. Real-time Trajectory Position Error Compensation Technology of Industrial Robot［J］. Measurement， 2023， 208：112418.

［12］ ?王眾，焦曉紅，程明星.船體除銹機械手的干擾抑制軌跡跟蹤控制［J］.中國機械工程，2018，29（6）：731-737.

WANG Zhong， JIAO Xiaohong， CHENG Mingxing. Trajectory Tracking Control with Disturbance Attenuation for Hull Derusting Manipulators［J］ China Mechanical Engineering， 2018，29（6）：731-737.

［13］ ?LI ?Jiangyang， ZOU Lai， LUO Guoyue， et al. Enhancement and Evaluation in Path Accuracy of Industrial Robot for Complex Surface Grinding［J］. Robotics and Computer-Integrated Manufacturing， 2023， 81：102521.

（ 編輯 張 洋 ）

作者簡介 ：

李默之 ，男，1999年生，碩士研究生。研究方向為車身薄板含膠成型制造。發表論文1篇。E-mail：limozhi@tongji.edu.cn。

朱文峰 （通信作者），男，1976年生，教授、博士研究生導師。研究方向為數字化設計與制造、智能制造。發表論文38篇。E-mail：zhuwenfeng@tongji.edu.cn。