電力動態負荷數據概率區間預測方法設計

許陳德

廣州供電局，廣東廣州 510000

0 引言

在電力系統中，可再生能源如風能和太陽能等規模的增加，使得電力負荷數據具有波動性和不確定性。由于可再生能源的不可控性，電力系統需要更準確的負荷預測來平衡供需，并保證電力網絡的穩定運行。電力負荷數據概率區間的預測實際上是一種十分復雜且繁瑣的工作，涉及電力系統日常的安全、穩定以及經濟運行等，預測結果的真實可靠，一定程度上可以進一步擴大實際的電力負荷控制強度，減少控制缺陷及誤差的出現，營造更加具體、完整的電力負荷管控環境。因此，預測電力動態負荷數據具有重要意義。

傳統的電力動態負荷數據概率區間預測形式多為單向的，如傳統SARIMA 模型動態負荷數據概率區間預測方法[1]、傳統改進雙向GABP 神經網絡動態負荷數據概率區間預測方法[2]，此類方法雖然能夠實現當前設定的預測需求及標準，但是缺乏針對性與穩定性，在復雜的電力負荷控制環境下，難以實現多目標協同調度，且在調控或者區間預測的過程中出現的預測誤差也會增加電力動態負荷的可控程度[3-4]。此外，單向的動態負荷數據概率區間預測結構整體的效率較低，對于負荷數據概率區間的預測速度較慢，這也是導致最終預測結果難以達到設定標準的關鍵因素之一。隨著電力市場的變化和負荷需求的復雜性增加，采用傳統方法預測負荷面臨著較大的不確定性。因此，需要引入概率區間預測來提供更準確的預測結果，并為電力系統運營商提供決策支持。

設計一種電力動態負荷數據概率區間預測方法，并從多個角度設計更加靈活多變的預測結構，在保證預測結果精準的同時，強化預測結果的可靠性，總結出對應的預測規律，為后續相關技術與行業的發展奠定堅實基礎。

1 電力動態負荷數據概率區間預測方法設計

1.1 電力動態負荷數據預處理

由于電力負荷數據具有動態性與針對性，在不同的電力執行環境下所形成的數據、信息也是不同的，且存在測量誤差、設備故障、數據缺失等，使得采集的數據質量和可靠性較低。因此，在針對負荷數據概率區間預測之前，必須先對采集的電力動態負荷數據預處理，避免后期出現不可控的預測誤差[5-6]。采集的數據中，缺失數據、異常數據的處理方式有所不同。

由于缺失數據是電力設備故障、系統故障或者傳輸網絡不穩定等復雜因素形成的，一般較難控制和捕捉，如果不及時處理，則會影響后期動態負荷區間預測的準確性[7]。考慮到電力負荷的周期波動性，結合傳感技術，對數據及相鄰數據加權處理，對其插補，電力負荷數據插補標準值x(a,b)如公式（1）所示：

式中，w表示可控制動態預測范圍；a表示基礎負荷感知區間；b表示偏振態重疊區間。結合當前的測算，采用調整預測數據插補的方式，強化缺失數據預處理感知整合效果。

由于復雜環境的變化、設備故障，甚至是突發事件，較容易出現異常用電情況，導致電路負荷動態管控過程中摻雜些許的異常數據。通過負荷感知技術采集外界信號，如線路中的電流與電壓以及功率信號、電力設備的溫度、設備檢測環境濕度與光照強度等信息，篩選出異常信號和異常值，以縱向對比法進行多感知范圍修正處理，得出單元性的感知處理標準值，異常感知標準值VS(E)如公式（2）所示：

式中，m表示可控異常數值總量；n表示異常值延伸規律，結合當前測試，完成對異常處理值的計算。基于得出的異常值和缺失數值，構建一個基礎性的負荷數據變動區間，完成對電力動態負荷數據預處理，匯總整合，以待后續的實踐應用。

1.2 電力負荷數據概率區間范圍壓縮

電力負荷的波動性和不確定性增加了電力系統的調度和運營難度，需要更多的靈活性和彈性。通過計算預處理后的電力動態負荷數據概率感知區間，可以提供更全面的預測結果，包括上下界情況，以應對不確定性和突發情況[8]。利用負荷傳感技術獲取預處理后的電力動態負荷數據的最佳偏振態可控區段，其中，合適值指在電力動態負荷管控區間內所形成的最佳預測感知標準數。

由于負荷傳感預測工作往往更加注重高準確率或者高合格率，但是測算的過程較容易受到外部環境及特定因素的影響，風險較大。所以，基于當前的預測需求，可以先壓縮預測的區間，將此區間劃分為多個區域，設置工作頻帶寬，并明確對應的動態范圍，此時，每一等寬度傳感區間形成的中間值也是區間感知測算得出的等效值，計算出小區間的預測合適值P：

式中，i表示等效測算次數；h1和h2分別表示基礎區間和實際區間；hi表示重復預測調制區間。結合當前的測算，獲取合適值和合適區間，完成區間壓縮。

1.3 負荷概率區間多層級劃分

由于傳統的電力動態負荷數據概率區間預測結構多設定為目標式，雖然可以實現預期的動態感知預測效果，但是較為單一，整體的預測效率較低，導致感知預測結果并不真實可靠，存在誤差。因此，利用獲取的數據概率感知區間合適值，設計采用多層級預測算法的邏輯結構，結合神經網絡技術，進行電力動態負荷區間層級分化，如圖1 所示。

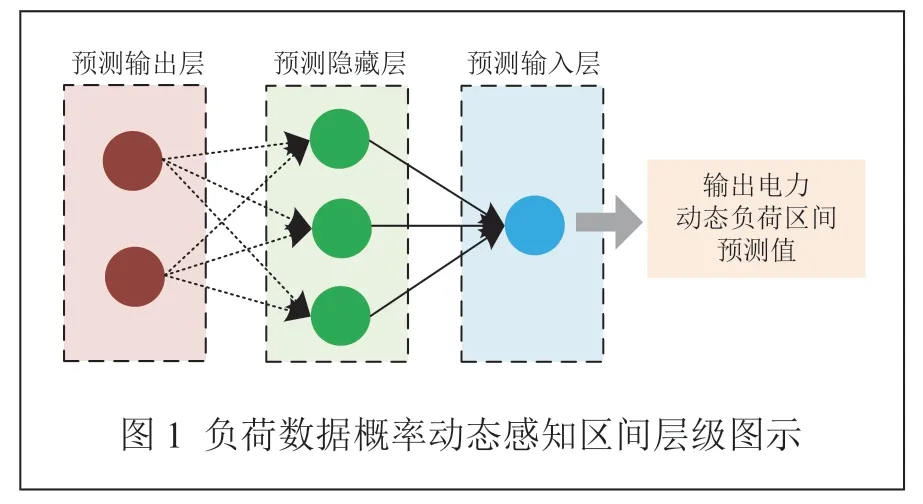
結合圖1，經負荷數據概率動態感知區間層級的分化處理，將當前的電力動態負荷概率合適區間劃分為多個識別敏感覆蓋層級。在各個層級之中設定對應的定向感知負荷參數，并設定多層級區間預測的可控指標及參數，如表1 所示。

結合表1，實現對多層級區間劃分，調整當前概率區間多層級區間，以多層級負荷區間的預測目標作為引導，獲取電力動態負荷概率區間的實時預測數值和信息。

1.4 電力動態負荷數據概率區間預測

根據多層級負荷概率區間層級劃分結果，設計電力動態負荷數據概率區間預測流程。在電力設備的總控平臺中設置負荷數據傳感的識別控制節點，節點的覆蓋區域不定，且節點之間相互關聯，形成對應的識別預測區域，便于實時數據、信息的采集匯總。通過相位調制的方式，對捕捉的外界異常信號進行動態化解析，結合傳播的負荷信號相位發生響應的變化程度，建立對應的負荷傳感信號映射變化量。每一個劃分的負荷數據概率區間都需要增設可識別控制階段，明確當前預測的頻帶寬[9]。實時的負荷數據動態響應的概率區間范圍M如公式（4）所示：

式中，U表示實時覆蓋區域；K表示重復預測區域；σ表示預測可控差值；O表示預測周期；b表示損失函數。基于此，完成電力動態負荷數據概率區間預測的設計，流程如圖2 所示。

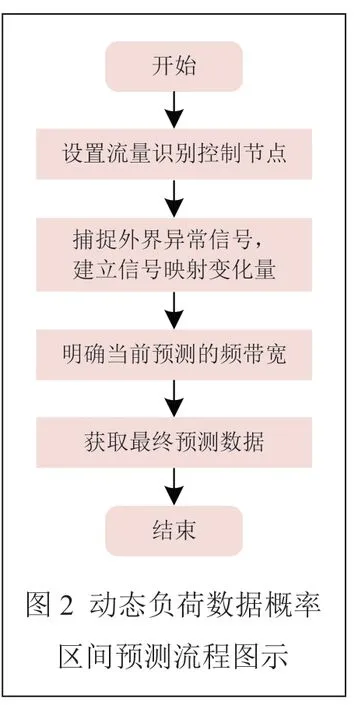
結合圖2，完成對動態負荷數據概率區間預測流程的設計與實踐應用。利用節點對電力動態負荷數值的變化以及區間進行調整，并采集相對應的實時數據、信息。以統一的格式對數據信息進行轉換，通過信道傳輸至預設的位置上，進行負荷概率區間預測調整處理。針對每一個區間進行實時負荷數據變化情況的預測，并對異常值作出標定，異常數值的出現一定程度上也代表預測誤差的形成。所以，利用傳感節點對電力負荷數據概率區間的預測結果進行實時調整，不僅可以保證負荷數據概率區間的穩定，還可以提升模型的綜合預測精度。

由于電力負荷數據的概率區間是不斷更新和變化的，為了及時更新和調整預測區間，以適應動態的負荷變化和系統需求的變化，采用多目標 PF-Elman 感知集成處理方法，對電力負荷數據概率區間預測結果展開短期的感知振態修正[10]，從而提供更準確和可靠的概率區間預測結果。集成處理方式主要劃分為4個階段，分別為分解聚類、子序列預測、帕累托最優方案設計以及多目標預測波長集成。

對預測區間的信號多層級解析，控制PF-Elman 感知集成差為1.02～2.15 之間，保證當前的傳感覆蓋感知區域在合理的范圍之內，針對模型中的預測感知矩陣，構建子序列預測目標，將原始的負荷數據分解為若干量，序列的層級分別為高頻子序列、低頻子序列以及趨勢子序列。選擇最優帕累托解集，獲取當前各個區間的預測數據，將數據與目標進行整合，測算出實時的預測集成值，一般控制在3.55～6.18 之間，判定當前動態負荷的預測結果是否精準，提升預測結果的真實可靠。需要注意的是，區間的預測標準以及集成范圍并不是固定的，可以隨著實際的需求作出改變和調整，擴大對應的預測范圍，為后續預測方法的創新與升級奠定堅實基礎。

2 方法測試與結果分析

為了驗證電力動態負荷數據概率區間預測方法的實際應用效果，對其展開分析與驗證研究。考慮到最終測試結果的真實性與可靠性，采用對比的方式展開分析，選定G 電力覆蓋區域作為測試的主要目標對象，選取文獻[1]的傳統SARIMA 模型動態負荷數據概率區間預測測試組、文獻[2]的傳統改進雙向GABP 神經網絡動態負荷數據概率區間預測測試組以及此次所設計的動態負荷數據概率區間預測測試組，對最終得出的預測結果比照研究。

2.1 測試準備

結合傳感技術，對選定的G 電力覆蓋區域電力動態負荷數據概率區間預測環境進行實時搭建，明確區間的預測范圍，并將其劃分為6 個測試感知區間。在G 電力覆蓋的區域布置電力負荷監測傳感器，將其安裝在變電站、配電箱、電纜線路等位置，實時采集電力系統的負荷數據。同時，在感知區間之內設置多個預測識別節點，節點之間互相搭建，形成循環性的預測結構。選取PowerFactory 作為實驗的軟件環境，其是一款功能強大的電力系統仿真和分析軟件，可以用于模擬和分析電網運行狀態、負荷變動和系統穩定性等。因此，利用該軟件實現分析G 電力覆蓋區域電力動態負荷變動情況。其中，預測等級表示對電力負荷未來變化的預測精度等級，在電力負荷預測中常用來評估方法的準確性和可靠性。同時，為了衡量電力負荷的變動程度，獲取G 電力覆蓋區域的波動比，即短期內電力負荷變動量與總負荷平均值之比。波動比較大時，表示負荷變動劇烈；波動比較小時，表示負荷相對穩定。此時，結合當前的電力狀態，進行電力負荷變動情況的分析，如圖3 所示。

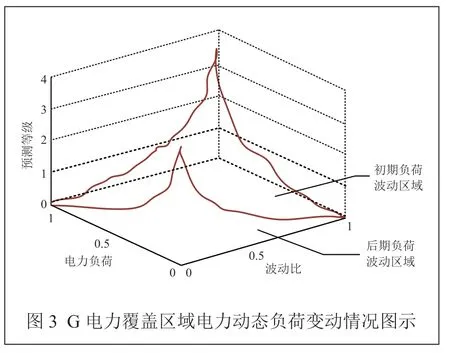
結合圖3，完成對G 電力覆蓋區域電力動態負荷變動情況的分析。其中，初期負荷波動區域是指電力負荷發生劇烈波動的時間段，通常表現為高頻率的變動，與突發事件、設備故障等因素有關；而后期負荷波動區域指電力負荷在較長時間內出現變動的時間段，通常表現為低頻率的波動，與季節變化、功率需求變化等因素有關。以此為基礎，對相應的區間進行振動覆蓋處理，并計算出允許出現的最大預測限制差值F：

2.2 測試過程及結果分析

在上述搭建的測試環境中，對G 電力覆蓋區域電力動態負荷數據概率區間預測方法進行設計與驗證分析，對選定的概率區間進行最優負荷相位感知預測值K的計算，如公式（6）所示：

式中，π表示基礎預測單元區間；ζ表示預測均值；ρ表示數據轉換比；λ表示預測實際值；T表示預測次數；B表示可控預測誤差。

APFE（Absolute Percentage Forecast Error）是電力動態負荷數據概率區間預測中常用的誤差指標，將其作為實驗的評價指標，用于衡量概率區間預測與實際觀測值之間的誤差，APFE 值越低，表明概率區間預測可信度越高，能夠準確地反映負荷真實情況。將獲取的最優負荷相位感知預測值作為預測標準值，通過捕捉電力負荷動態變化的信號，明確數據概率區間的實際預測定值，計算出APFE 值，如公式（7）所示：

式中，I表示APFE 值；γ表示初始預測波動范圍；β表示實際波動范圍；?表示定向預測差值；τ表示重復預測均值；Z表示實時預測范圍。結合當前測試，完成對測試結果數據的分析，具體如表2 所示。

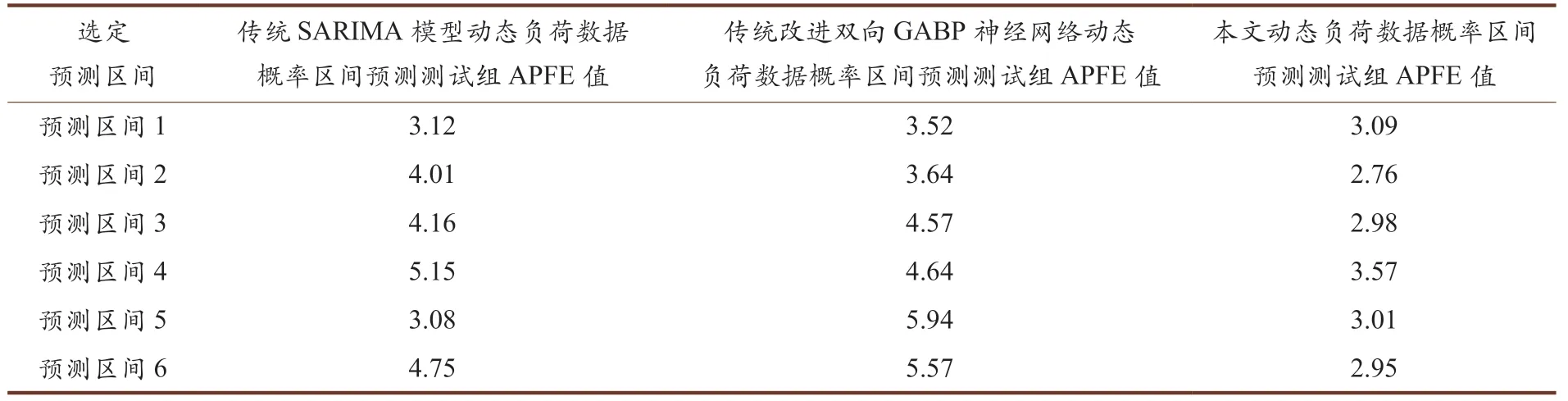
表2 測試結果數據分析表

結合表2，可以得出以下測試結論：對比于傳統SARIMA 模型動態負荷數據概率區間預測測試組、傳統改進雙向GABP 神經網絡動態負荷數據概率區間預測測試組，此次所設計的動態負荷數據概率區間預測測試組最終得出的APFE 值均被較好地控制在4 以下，說明當前所設計的預測方法更加靈活、高效，預測的效率更佳，具有實際的應用價值。

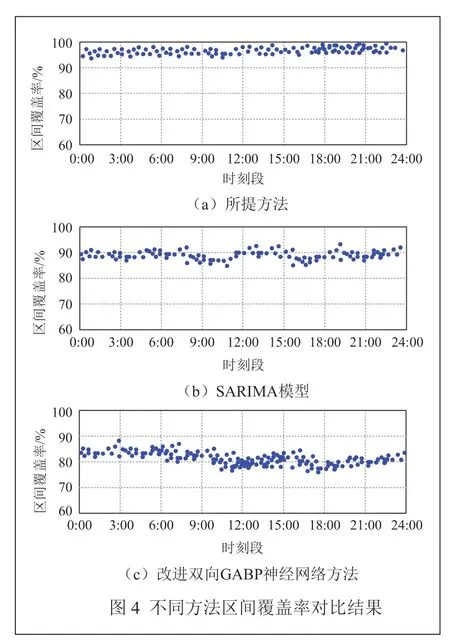
為了進一步驗證不同方法概率區間預測的有效性，將區間覆蓋率作為評估指標，區間覆蓋率越高，表示預測結果越可靠。由于時間是評估動態負荷預測方法的重要維度，選擇時間維度為一天24 h，每3 h 進行一次預測，觀察和比較不同方法預測結果的區間覆蓋率隨時間的變化情況，如圖4 所示。

根據圖4 可知，所提方法在一天時間內，預測結果的區間覆蓋率都在95%以上，表明與實際負荷數據之間的一致性和可靠性較高，而其他兩種方法的區間覆蓋率低于91%，從而驗證了所提方法具有較高的應用性能。這是因為所提方法采用了多層級的方式，擴大了預測范圍，提升了模型的綜合預測精度。

3 結束語

上述分析是對本文的電力動態負荷數據概率區間預測方法的設計與驗證。與初始的電力動態負荷數據概率區間預測結構相比，此次結合當前的測試需求，先依據傳感技術，設計更加靈活多變的預測結構，從多個角度強化實際的預測空間與實際覆蓋范圍，通過概率區間法的輔助，最大程度上擺脫對負荷數據概率區間預測經驗的依賴，實現人機交互預測處理，消除影響最終預測結果的不穩定因素，為該項技術的發展提供參考。