Dilation,discrimination and Uhlmann’s theorem of link products of quantum channels

Qiang Lei(雷強), Liuheng Cao(操劉桁), Asutosh Kumar, and Junde Wu(武俊德)

1School of Mathematical Sciences,Harbin Institute of Technology,Harbin 150001,China

2Department of Physics,Gaya College,Magadh University,Rampur,Gaya 823001,India

3School of Mathematical Sciences,Zhejiang University,Hangzhou 310027,China

Keywords: quantum channels,link products,Stinespring dilation theorem,Uhlmann’s theorem

1.Introduction

In quantum computation and information processing, a number of measurements and transformations are called into action depending on the specific task to be performed.A quantum network,which is an assembly or combination of a sufficient number of elementary circuits that transform or measure quantum states, can be used in a number of different ways to accomplish different tasks.Various transformations are brought about by quantum operations or quantum channels.A quantum channel is a linear map or quantum operation that is completely positive and trace-preserving.It can be imagined as a unitary interaction of a system with an environment.Quantum channels essentially describe how quantum information is transformed when it passes through physical systems,including potential sources of noise and errors.

Quantum channel dilation refers to the process of constructing a new and better quantum channel by introducing additional qubits on a noisy quantum channel.Quantum channel dilation is widely used in quantum key distribution,quantum state transmission, and quantum error correction.It can facilitate realization of efficient quantum communication and information processing.[1-4]According to the Stinespring dilation theorem, any quantum channel can be implemented as an isometric channel in a larger system.

In order to ensure the reliability and security of information transmission,it is necessary to distinguish different types of quantum channels in quantum communication.This problem has been considered by many researchers.[5-12]Quantum channel discrimination technology can be applied to various quantum communication protocols,such as quantum key distribution, quantum remote state preparation, and quantum algorithms.

The link product theory of quantum channels[13]is an important tool for studying quantum networks.[13-18]Link product is the operation that connects two quantum networks.In this paper, we establish the Stinespring dilation theorem of link product of quantum channels in two different ways.We discuss the discrimination of quantum channels and show that the distinguishability can be improved by considering the link product of each quantum channelntimes for largen.We also find that the maximum value of Uhlmann’s theorem can be achieved for diagonal channels.

2.Stinespring dilation theorem of link product of quantum channels

2.1.Preliminaries and notation

Let?be a finite dimensional Hilbert space and?(?)be the set of linear operators on?.?(?0,?1)denotes the set of linear operators from?0to?1.The set of linear maps from?(?0)to?(?1)is denoted by?(?(?0),?(?1)).I0≡I?0is the identity operator in?0,?0≡??(?0)is the identity map on?(?0),Tr0≡Tr?0is the partial trace over?0,and so on.Furthermore,MTxydenotes the transpose over?x ??y, andMTyxydenotes the partial transpose over?y.

Choi isomorphism is a one-to-one correspondence map C:?(?(?0),?(?1))→?(?1??0)defined as

whereV ∈?(?0,?1)andV?V=I0.[19]

2.2.Stinespring dilation theorem of composition of quantum channels

The Stinespring dilation theorem states that every quantum channel can be realized as an isometric channel on a larger system.

Lemma 1 (Stinespring dilation theorem)[20]LetM10∈?(?1??0) be the Choi operator associated with the quantum channel? ∈?(?(?0),?(?1)),and let?Abe the Hilbert space?A=Supp(M10).Then,a minimal dilationV:?0-→?1??Ais given by

where Tr0,1,2denotes the partial trace over the Hilbert spaces?0,?1and?2,respectively.

This construction of the Stinespring dilation of composition of quantum channels is simple to manipulate.However,the ancilla dimension is not minimum.In the following we give another dilation ofN °?such that the ancillary space has the minimum dimension.

Theorem 2 Let? ∈?(?(?0),?(?1)) andN ∈?(?(?1),?(?2)) be two quantum channels andM10∈?(?1??0),N21∈?(?2??1)be their corresponding Choi operators,and?A=Supp(C(N°?)).Then there is a minimal isometry dilationV:?0-→?2??Agiven by

Remark 1 The above two approaches have their own merits and demerits.The dilation method in Theorem 1 corresponds to indirect composition dilation and is easier to implement.However, it may cause waste of resource.The way in Theorem 2 is a direct composition dilation.Similar to the proof in Ref.[17], the isometric dilation given in Theorem 2 has a minimum ancilla dimension.It can minimize resource waste but requires more computational and communication resources.For example, suppose rank(?)=rank(N)=16.In the case of indirect composition dilation, dim(?A1)=16, dim(?A2)=16.Although the required space resource?Ahas a dimension of 256,it belongs to two systems and only 16-dimensional calculations are required.On the other hand, in the case of direct composition dilation, dim(?A)=rank(N °?)≤256.The dilated space belongs to only one system,and the computational dimension can reach up to 256.Therefore, in specific applications, we need to choose the appropriate dilation method according to the actual situation to achieve the optimal effect.

2.3.Stinespring dilation theorem of link product of quantum channels

If we consider quantum channels such that their input and output spaces are the tensor product of Hilbert spaces, it is possible to compose these channels only through inserting or pasting some of these spaces or identity channels.This operation is called link product.At this time, the link product of two quantum channels?andN, denoted byN ??, is an important tool of studying the quantum network theory.[17]

It then follows that using Theorems 1 and 2, we can get the following Stinespring dilation theorems of link product of two quantum channels.

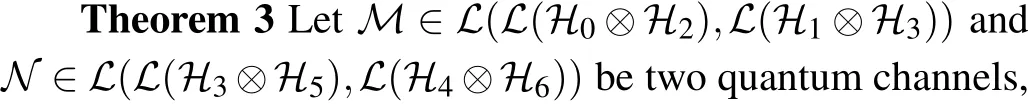
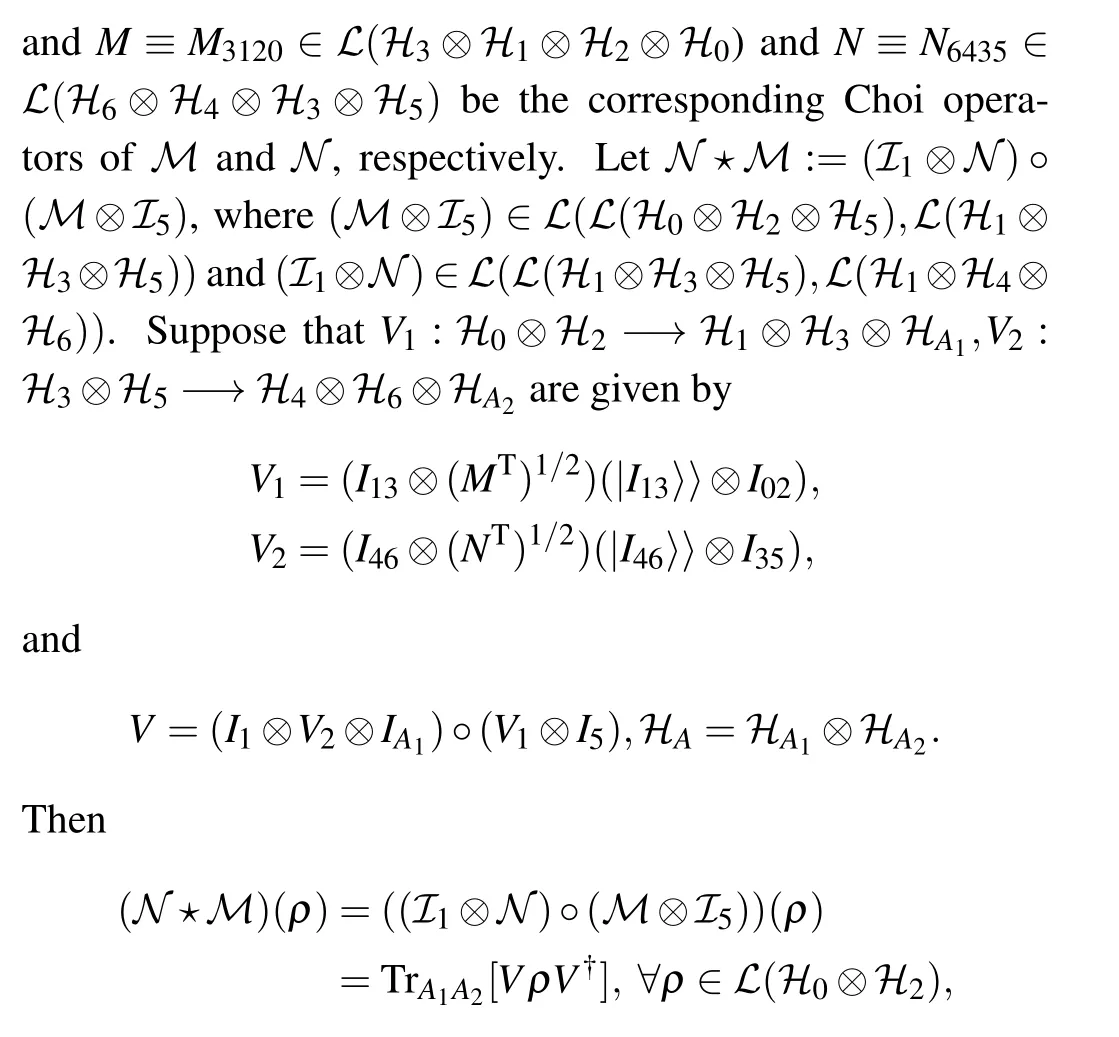
whereIA1is the identity map on?A1,I1is the identity map on?1andV?V=I025.

3.Discrimination of quantum channels

Given two density operatorsρandσ,the fidelity

quantifies the extent to whichρandσcan be distinguished from one another.[5]It is obvious that 0≤F(ρ,σ)≤1,F(ρ,σ)=1 if and only ifρ=σ(ρandσare indistinguishable) andF(ρ,σ) = 0 if and only ifρ ⊥σ(ρandσare completely distinguishable).

For quantum channels,the fidelity is defined by the Choi operators.Let?,N ∈?(?(?0),?(?1))andM,N ∈?(?1??0)be their corresponding Choi operators.The fidelity of?andNis defined by

whered0=dim(?0) andFis the fidelity of states.[5]Similar to the fidelity of density operators, when?andNare orthonormal, that is,?(?,N)=0,?andNcan be completely distinguished.Nevertheless, when?is not orthogonal toN,then 0＜?(?,N)＜1,?andNcannot be fully distinguished.

Now we show that the distinguishability of quantum channels?andNcan be improved by considering link product of each quantum channelntimes,asngrows.For that we first take into account the following two lemmas.

Lemma 2Let?,N ∈?(?(?0),?(?1)) be two quantum channels andM,Nbe their corresponding Choi operators.ThenM ?Nis the Choi operator of??N.

ProofLetTbe the Choi operator of??N.According to definition,we have

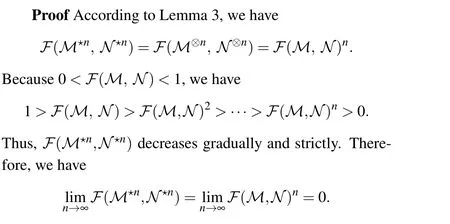
For?ε ＞0,?n(a natural number) and ?N= [log?(?,N)ε],such that whenn ＞?N,we have 0＜?(??n,N?n)＜ε.Thus the distinguishability of?andNis improved gradually asngrows.

4.Uhlmann’s theorem for the fidelity of diagonal channels

Let? ∈?(?(?0),?(?1)) be a quantum channel with dim(?0)=dim(?1)=2.We consider an orthonormal basis consisting of the Hermitian matrices,[21,22]

Quantum channelsC,D,?, andSare called depolarizing,transpose depolarizing,hybrid depolarizing classical,and hybrid transpose depolarizing classical, respectively.They are among the most widely used channels in science and technology.[21,23-26]

LetC,D,RandSbe the Choi operators ofC,D,?andS,respectively.According to the calculation method of Choi operator in Ref.[22],we can obtain

whereαi,βi,i=1,2,3,4 are the eigenvalues ofM,Nrespectively,andM,Nare Choi operators of?,N.

Uhlmann’s theorem for the fidelity of quantum channels[5]is stated as

5.Conclusion

In summary,we have established the Stinespring dilation theorem of the link product of quantum channels in two different ways and discussed the discrimination of quantum channels.It is shown that the distinguishability can be improved by self-linking each quantum channelntimes asngrows.We also find that the maximum value of Uhlmann’s theorem can be achieved for diagonal channels.

Acknowledgment

Project supported by the National Natural Science Foundation of China (Grant Nos.61877054, 12031004, and 12271474).