ESTIMATE ON THE BLOCH CONSTANT FOR CERTAIN HARMONIC MAPPINGS UNDER A DIFFERENTIAL OPERATOR*

(陳潔玲) (劉名生)

School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China E-mail: 1304889502@qq.com; liumsh@scnu.edu.cn

Abstract In this paper, we first obtain the precise values of the univalent radius and the Bloch constant for harmonic mappings of the form L(f) = zfz -, where f represents normalized harmonic mappings with bounded dilation.Then, using these results, we present better estimations for the Bloch constants of certain harmonic mappings L(f), where f is a K-quasiregular harmonic or open harmonic.Finally, we establish three versions of Bloch-Landau type theorem for biharmonic mappings of the form L(f).These results are sharp in some given cases and improve the related results of earlier authors.

Key words Bloch-Landau type theorem; Bloch constant; linear complex operator; harmonic mapping; biharmonic mapping; univalent

1 Introduction

A twice continuously differentiable complex-valued functionf(z)=u(z)+iv(z)in a domainD ?C is said to be harmonic iffsatisfies the harmonic equation Δf=0, where Δ represents the Laplacian operator

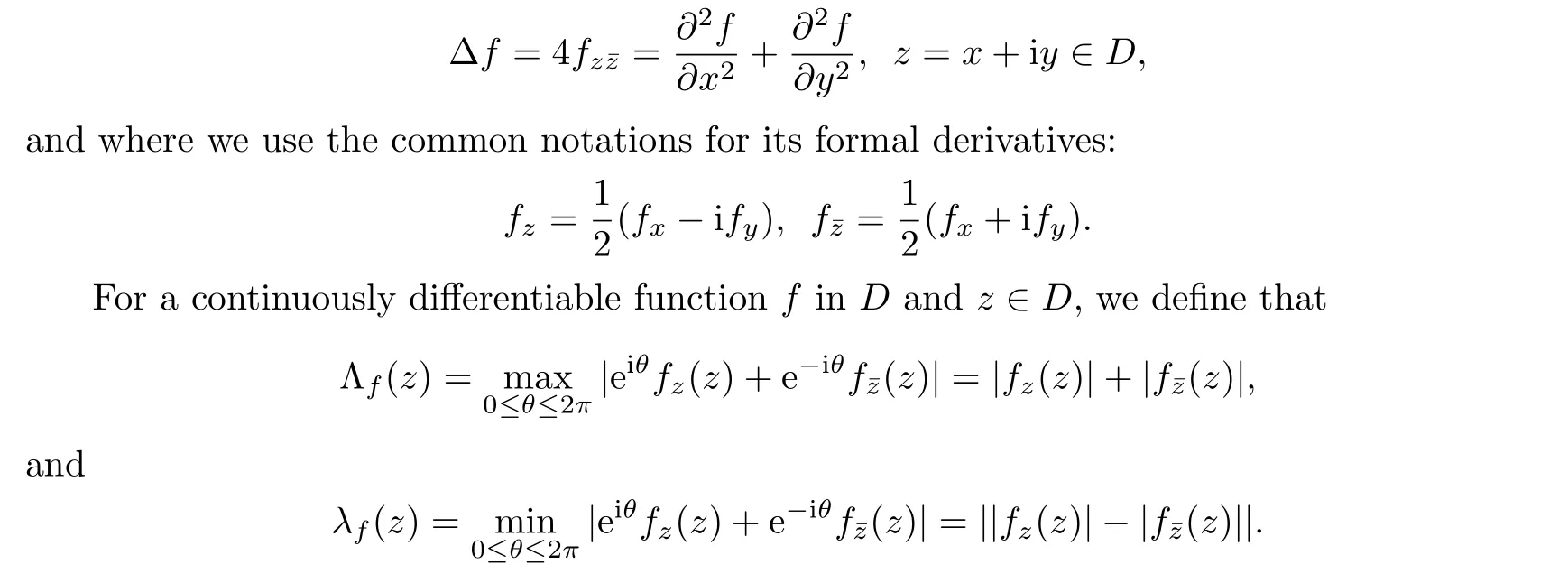
We denote the Jacobian offbyJf.Lewy [19] showed that a harmonic mappingf(z) is locally univalent in a domainDif and only ifJf/= 0 for anyz ∈D.Of course, the local univalence offdoes not imply global univalence in a domainD.It is evident that|Jf|=Λfλf.A harmonic mappingfis said to beK-quasiregular(K ≥1)on a domainDif Λf ≤Kλfholds everywhere onD.Recall that a mapping of the unit diskU={z ∈C :|z|＜1}is said to be an open mapping if it maps any open subset ofUto an open set in C.

A four times continuously differentiable complex-valued functionF(z)=U(z)+iV(z)withU(z) andV(z) being real-valued is called biharmonic in a domainD ?C if and only if ΔFis harmonic inD, i.e.,F(z) satisfies the equation

Harmonic mappings can be regarded as generalizations of holomorphic functions, and biharmonic mappings can be regarded as generalizations of harmonic mappings.Biharmonic mappings arise in many physical situations, particularly in fluid dynamics and elasticity problems, and have many important applications in engineering (see [1] for more details).It is known ([1]) that a mappingF(z) is biharmonic in a simply connected domainDif and only ifF(z) has the representation

whereaandbare complex constants and,fandgare complex functions in C.In addition,the operatorLpossesses a number of interesting properties.For instance, it is easy to see that the operatorLpreserves both harmonicity and biharmonicity.Many other basic properties are stated in [2, 33].

In 2000,under a suitable restriction,Chenet al.[6]established two versions of the Landautype theorem for bounded harmonic mapping on the unit disk.Better estimates were given in [7-10, 14-16, 18, 22, 23, 28].Many authors also considered the Landau-type theorems for biharmonic mappings (see [3, 12, 21, 26]).In particular, the sharp version of the Landau-type Theorem of harmonic mappings with a bounded dilation, or Theorem 4 of Chen et al.in [6]was obtained in [18, 22, 23], which has been generalized to the cases of Biharmonic mappings and polyharmonic mappings in [26, 27].Moreover, Liuet al.[24] established the Landautype theorems for certain bounded harmonic mappings of the formL(f).In 2013, Huanget al.[17] estimated the univalent radius and Bloch constants for planar harmonic mappings of the formL(f), which improved some results of [24].In the same year, Chenet al.[11]proved the existence of a Landau constant for the class of functions of the formL(f), wherefisp-harmonic in|z|＜1.Liuet al.[20, 31] investigated the sharp estimates of quasi-convex mappings and the Bohr-type inequalities for holomorphic mappings with a lacunary series.X.S.Liu [32] investigated the sharp distortion theorems for a class of biholomorphic mappings in several complex variables.In 2019, Aghalaryet al.[4] established two versions of the Landautype theorem for certain bounded biharmonic mappingsL(f).However, few sharp results of Landau-type theorems for such harmonic mappingsL(f) have been found.To state our main results, we recall a result of Huanget al.in [17], which improved Theorem 2.3 of [24].

Theorem A([17,Theorem 2.5]) Letf(z)be a harmonic mapping of the unit diskUwithf(0)=λf(0)-1=0, and let Λf(z)≤Λ forz ∈U.ThenL(f) is univalent in the diskUt1andL(f)(Ut1) contains a schlicht diskUs1, where

The result is sharp when Λ=1.

It was shown in [6] that there is no Bloch theorem for harmonic mappings even with the normalizationfz(0) = 1,(0) = 0.However, there are Bloch theorems for a K-quasiregular harmonic mapping or an open planar harmonic mapping with the above normalization [6].Moreover, there are Bloch theorems for the subclasses of harmonic mappings of the formL(f),wherefis K-quasiregular harmonic mappings or open planar harmonic mappings with the above normalization [24].We recall a Bloch theorem of Liu et al.in [24] as follows:

Theorem B([24, Theorem 2.6]) Letf(z) be an open harmonic mapping of the unit diskUnormalized byfz(0)-1=(0)=0.ThenL(f)(U) contains a schlicht disc of a radius of at leastσ ≈0.014333.

Liuet al.also established analogous results for biharmonic mappings in [25, 29] as follows:

Theorem C([29, Theorem 3.2]) LetF(z)=|z|2g(z)+h(z) be a biharmonic mapping of the unit diskUwithλF(0) =λg(0) = Λg(0) = 1, Λg(z)≤Λ1and let Λh(z)≤Λ2forz ∈U.Then Λ1≥1, Λ2≥1,L(F) is univalent in the diskUt2andL(F)(Ut2) contains a schlicht diskUs2, wheret2is the unique root in (0,1) of the equation

However, Theorems A and D are not sharp for Λ＞1 andM ＞0, Λ＞1, respectively,Theorem C is not sharp for Λ1＞1, Λ2＞1, and Theorem C has the strong hypothesis thatλg(0)=Λg(0)=1.It is then natural to raise the following problem:

Problem 1.1 Can we improve the results in Theorems A, B, C and D? Can we establish several sharp results?

In this paper, by extending the method and techniques used in [26, 28], we will improve Theorems A, B, C and D.In particular, we will establish the sharp form of Theorem A (see Theorem 3.1).These results will present an affirmative answer to Problem 1.1.

2 Preliminaries

In order to establish our main results, we need the following notions and lemmas:

Proof AsLis linear andL（|z|2）=0, we have thatL(F)=|z|2L(g).Then

Lemma 2.10Suppose that Λ＞1.Letf(z) be a harmonic mapping of the unit diskUwithf(0)=λf(0)-1=0 and let Λf(z)＜Λ for allz ∈U.Then, for eachz=reiθ ∈?Ur(0＜r ＜1),

ProofSincef(z) is a harmonic mapping in the unit diskUandL(f) =zfz-, we see that=0,

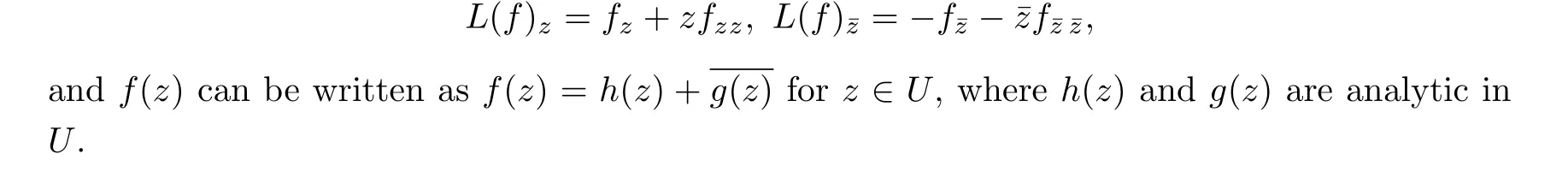
Hence, the inequality (2.4) follows from (2.5), (2.6) and (2.7).The proof is complete.□

3 Bloch-Landau Type Theorems of Certain Harmonic Mappings

Now, using Theorem 3.1, we consider the case wherefis aK-quasiregular harmonic mapping.

Theorem 3.3 Letf(z) be aK-quasiregular harmonic mapping of the unit diskU, withf(0) =λf(0)-1 = 0.ThenF(z) :=L(f)(z) is a harmonic mapping of the unit diskUwithF(0)=λF(0)-1=0, andL(f)(U) contains a schlicht disc of a radius of at least

Thus it follows from Theorem 3.1 thatL(g) is univalent onUρ0, and thatL(g)(Uρ0) contains a schlicht diskUσ0, where

The proof is complete.□

Finally, we improve Theorem B as follows:

Theorem 3.4 Letf(z) be an open harmonic mapping of the unit diskUnormalized byfz(0)-1 =(0) = 0.ThenF(z) :=L(f)(z) is a harmonic mapping of the unit diskUwithF(0)=λF(0)-1=0, andL(f)(U) contains a schlicht disc of a radius of at least

which improves the radius 0.014333 of Theorem B or Theorem 2.6 in [24].□

4 Bloch-Landau Type Theorems of Certain Biharmonic Mappings

In this section, we first establish an improved version of Theorem C.

(ii) If Λg(z)≤Λ1and Λh(z)≤1 or|h(z)|≤1 forz ∈U, thenL(F) is univalent in the diskUr′3, andL(F)(Ur′3) contains a schlicht diskUR′3, wherer′3is the unique root in (0,1) of the equation

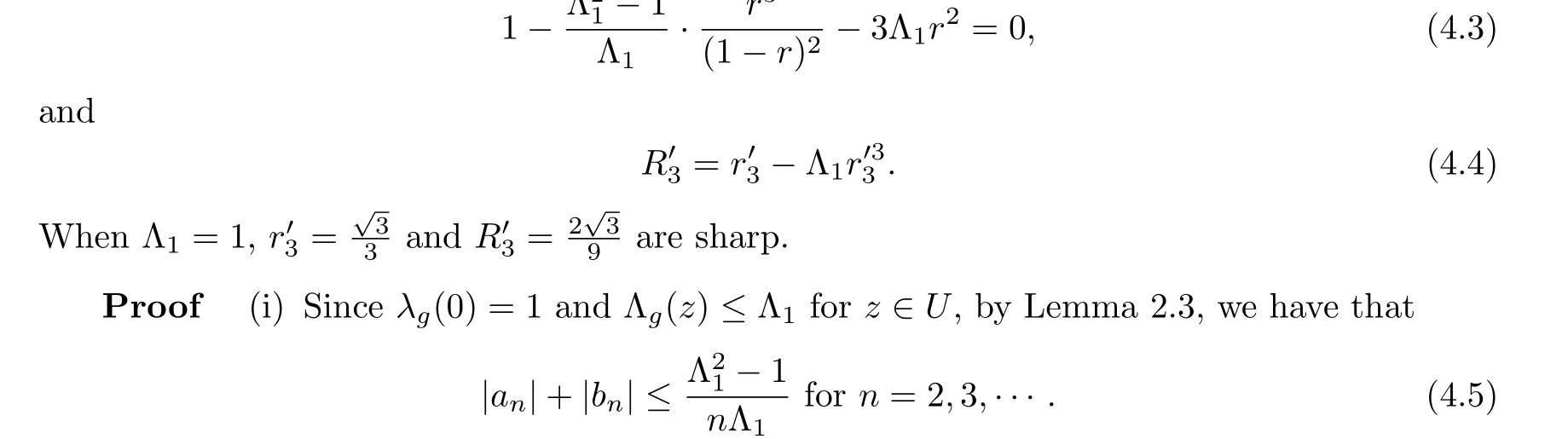
We first prove the univalence ofL(F) inUr3.To this end, we choose two distinct points,z1andz2, inUr(0＜r ＜r3), noting thatλF(0)=λh(0)=λg(0)=1 and that Λh(z)＜Λ2forz ∈U, so we obtain, from Lemmas 2.6, 2.8, 2.9 and (4.5) that

Hence,L(F) is univalent in the diskUr3, andL(F)(Ur3) contains a schlicht diskUR3.

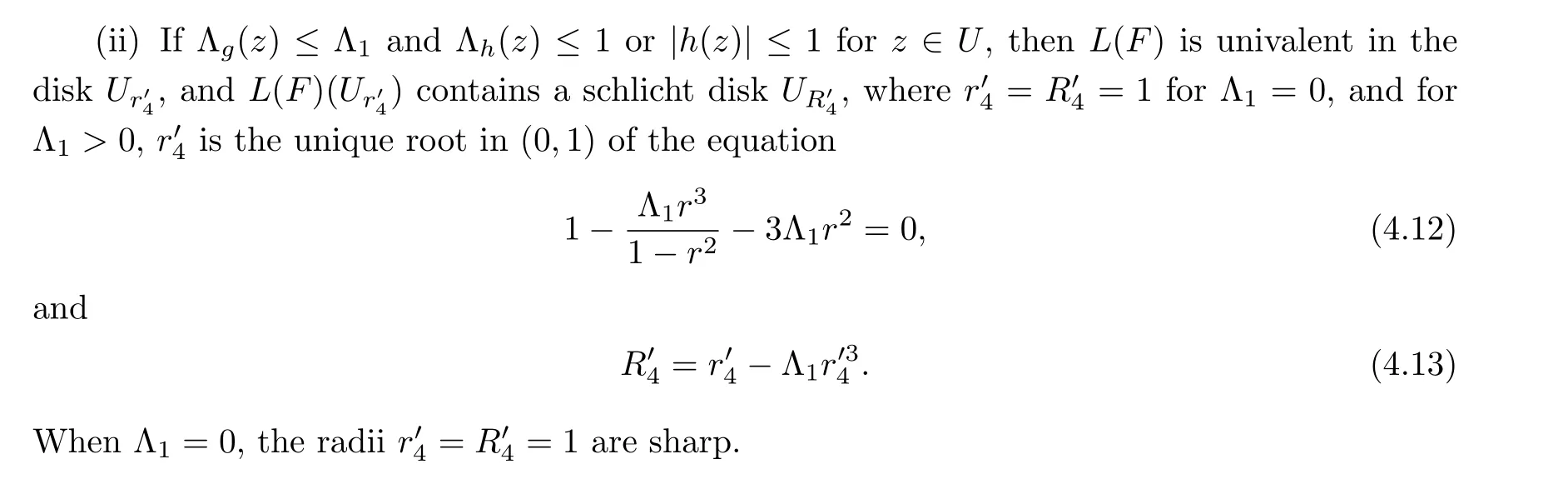
Remark 4.3From Table 1, we can see that, for the same Λ1and Λ2,r3＞t2,R3＞s2andr4＞t2,R4＞s2.

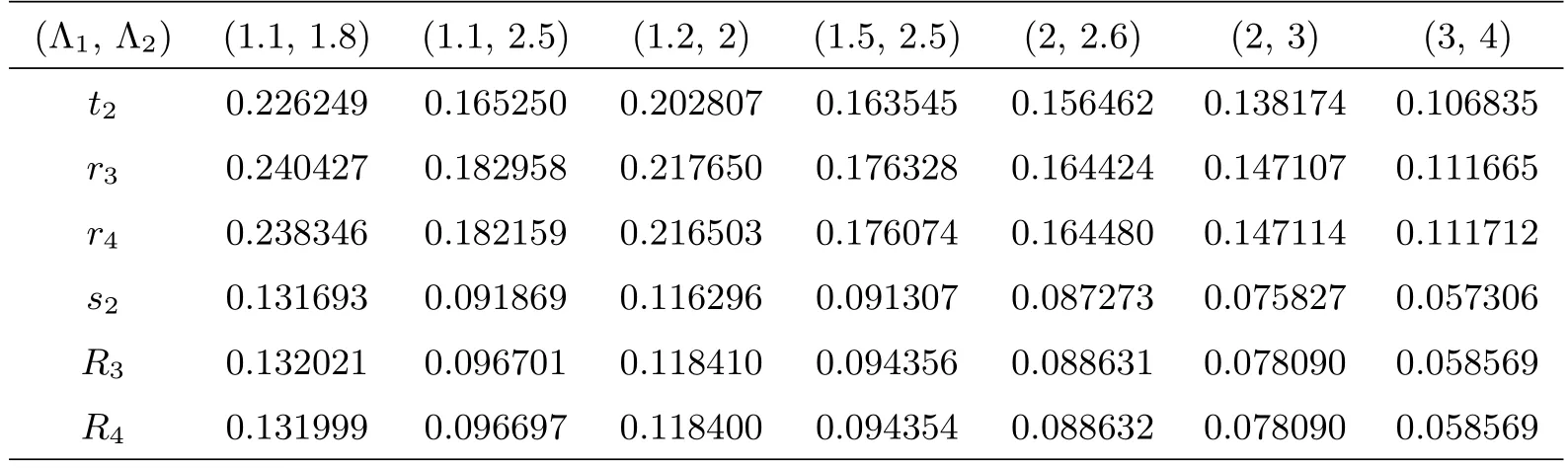
Table 1 Values of r3, R3; r4, R4; t2, s2 in Theorems 4.1, 4.2 and C

(ii) If|g(z)|≤Mand Λh(z)≤1 or|h(z)|≤1 forz ∈U, thenL(F) is univalent in the diskUr′5, andL(F)(Ur′5) contains a schlicht diskUR′5, wherer′5=R′5= 1 forM= 0, and forM ＞0,r′5is the unique root in (0,1) of the equation

Hence,L(F) is univalent in the diskUr5, andL(F)(Ur5) contains the diskUR5.

Now we prove (ii).If|g(z)|≤Mand Λh(z)≤1 or|h(z)|≤1 forz ∈U, similarly to the proof of Theorem 4.1 (ii), we first prove thatL(F) is univalent inUr′5.In fact, forz1,z2∈Ur(0＜r ＜r′5,z1/=z2), and by (4.8), we have that

Hence,L(F)(Ur′5) contains a schlicht diskUR′5.This completes the proof.□

Remark 4.5From Table 2, we can see that for the sameMand Λ,r5＞t3,R5＞s3.

Table 2 Values of r5, R5 in Theorem 4.4, and the corresponding values of t3 and s3 in Theorem D

Conflict of InterestThe authors declare no conflict of interest.