THE EXACT MEROMORPHIC SOLUTIONS OF SOME NONLINEAR DIFFERENTIAL EQUATIONS*

(劉慧芳)

School of Mathematics and Statistics, Jiangxi Normal University, Nanchang 330022, China E-mail: liuhuifang73@sina.com

Zhiqiang MAO (毛志強)

School of Mathematics and Computer, Jiangxi Science and Technology Normal University,Nanchang 330038, China E-mail: maozhiqiang1@sina.com

Abstract We find the exact forms of meromorphic solutions of the nonlinear differential equations

Key words Nevanlinna theory; nonlinear differential equations; meromorphic functions;entire functions

1 Introduction and Main Results

For any given differential equation in the complex domain, one of most important and difficult problems is to find all of the entire or meromorphic solutions.In [11], Yang and Li considered the nonlinear differential equation

whereP(z,f) is a polynomial infand its derivatives with small functions offare its coefficients,p1,p2are polynomials, andα1,α2are distinct nonzero constants (see, e.g.[6-9, 13]).Recently,Gundersen and his co-author[3]perturbed eq.(1.1)by multiplying polynomials to its coefficients, and proved the following result:

Theorem B([3]) Letp(z)andq(z)be nonzero polynomials,and letα(z)be a nonconstant entire function.If the differential equation

admits an entire solutionf(z),thenα(z)=3az+bfor some constantsa,b,andp,qare constants satisfying that 27p=4q3a6.Moreover,f(z) has the form

Note that in Theorems A and B,the coefficients of the differential equations are polynomials whose growth is dominated by their entire solutions.Naturally,the question to be asked is: does eq.(1.1)admit entire or meromorphic solutions if its coefficients are perturbed by transcendental functions? Furthermore, if such solutions exist, what about their forms? The main purpose of this paper is to give some answers concerning these questions.

Theorem 1.1Letkbe a positive integer, and letb,pj(j= 0,1,2),α1,α2be nonzero constants withα1/=α2.If the nonlinear differential equation

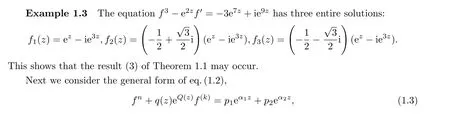
and obtain the following result:

Theorem 1.2Letn,kbe positive integers withn ≥4, letq(z),Q(z) be nonzero polynomials such thatQ(z)is not a constant,and letp1,p2,α1,α2be nonzero constants withα1/=α2.If eq.(1.3)admits a meromorphic solutionf(z)satisfying thatN(r,f)=S(r,f),then degQ=1 andq(z) leads to a constant such that

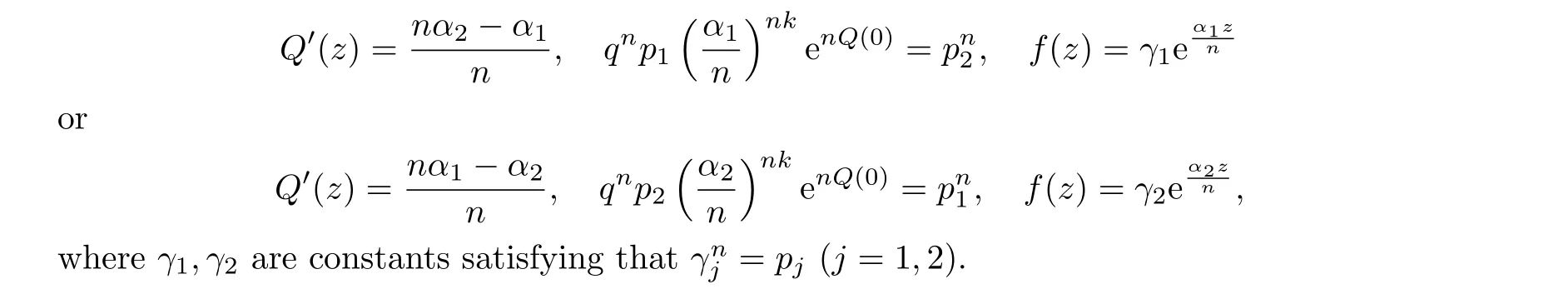
There exists examples of Theorem 1.2.For example,f(z) = ie2zsolves the differential equationf4+2iezf(k)=e8z-2k+1e3z.

In the above results, the Nevanlinna theory of meromorphic functions is an important research tool.We assume that readers are familiar with the basic notations and results of Nevanlinna theory, such asm(r,f),N(r,f) andT(r,f), the first and second main theorems,and the lemma on the logarithmic derivative (see [4, 5, 12]).The notationS(r,f) denotes any quantity satisfying thatS(r,f) =o(T(r,f)) asr →∞, possibly outside a set of finite linear measure.In this paper,we will combine the Nevanlinna theory of meromorphic functions and its Cartan’s version to prove our results.The latter plays a key role in estimating the integrated counting function of solutions of eqs.(1.2) and (1.3).Concerning Cartan’s version of the Nevanlinna theory, we refer readers to [1] and [2].

2 Lemmas

Lemmas 2.2 and 2.3 are Cartan’s version of the Nevanlinna theory, in which Lemma 2.2 is the simple form of Cartan’s second main theorem.

Lemma 2.2([1, 2]) Letf1,f2,···,fpbe linearly independent entire functions.Assume that, for each complex numberz, max{|f1(z)|,···,|fp(z)|}＞0.Forr ＞0, set that

Lemma 2.4([12]) Letfbe a nonconstant meromorphic function, and letkbe a positive integer.Then

(ii) for 1≤j ＜k ≤n,gj-gkare not constants;

(iii) for 1≤j ≤n,1≤t ＜k ≤n,T(r,fj)=o{T(r,egt-gk)}(r →∞,r/∈E1).Thenfj(z)≡0 (j=1,···,n).

Lemma 2.6Under the conditions of Theorem 1.2, if eq.(1.3) admits a meromorphic solutionf(z) satisfying thatN(r,f)=S(r,f), then degQ=1.

ProofLetf(z) be a meromorphic solution of eq.(1.3) such thatN(r,f) =S(r,f).Supposing that degQ ＞1, from eq.(1.3) and the Lemma on the logarithmic derivatives, it follows that

Combining (2.6) andN(r,ψ) =S(r,f), we have thatT(r,f) =S(r,f).This is absurd, so degQ=1.□

3 Proofs of Results

Proof of Theorem 1.1Lettingf(z)be an entire solution of eq.(1.2),from eq.(1.2)and Lemma 2.5, it follows thatf(z) is transcendental and that

Thus the result (1) of Theorem 1.1 holds.

Differentiating (3.10) and eliminating eα2zagain, we get that

whereQ1(z) =-p0φ1(z), and by (3.15) and (3.14), we know thatQ1(z) is an entire function satisfying that

Now we discuss two cases.

Case 1 Suppose thatp1eα1z,p2eα2zand-q(z)eQ(z)f(k)(z)are linearly dependent.Then,using an argument similar to that for Case 1 in the proof of Theorem 1.1, from eq.(1.3) and Lemma 2.1, it follows that

We write eq.(1.3) in the form

wherec1,c2are constants.Then, by (3.59) and Lemma 2.1, we have thatc1/= 0,c2= 0 orc1=0,c2/=0.This gives thatf(z) has the form (3.50).Thus by using an argument similar to that for Case 1, we obtain the result of Theorem 1.2.

Ifφ/≡0, then, by (3.55), Lemma 2.4 and the expression ofD, we obtain that

Conflict of InterestThe authors declare no conflict of interest.