基于共形幾何的面部模型插值構建算法
龐 敏,張 元,熊風光,焦世超,霍昕恬
(1.中北大學 計算機科學與技術學院,山西 太原 030051;2.中北大學 機器視覺與虛擬現實山西省重點實驗室,山西 太原 030051;3.中北大學 計算機科學與技術學院 山西省視覺信息處理及智能機器人工程研究中心,山西 太原 030051;4.太原理工大學 信息與計算機學院,山西 太原 030023)
0 引 言
三維面部模型構建是計算機視覺、虛擬仿真領域的重要研究方向[1,2]。傳統三維面部模型構建方法包括掃描建模、基于圖像建模和基于三維模型重構建模。
研究者利用三維掃描設備對面部掃描得到高質量模型的方法成本高、耗時長、要求被掃描對象姿態穩定。這些特點造成該方法多適用于實驗室[3],且不易獲取連續維度多表情面部模型。
基于圖像的三維建模方法難以準確體現面部包含的高頻信息,容易丟失褶皺、酒窩等細節[4,5]。侯守明等[6]提出三維人臉建模算法利用Kinect獲取對象的色彩和深度信息,依據彩色圖像建立標準面部模型,再結合深度信息對其進行拉普拉斯變形得到真實感更強的三維模型。汪淑賢等[5]提出基于圖像的三維重建算法,選取同一面部不同朝向的多張圖像后再根據顏色信息進行聚類、分割獲取面部輪廓,基于輪廓包含的特征對面部圖像立體匹配,獲取帶有深度的稀疏視差圖進而生成面部模型的平滑點云。
基于三維變形的模型重構方法包括自由變形、骨骼變形、微分變形和基于深度學習的變形。自由變形和骨骼變形均不適用,因為他們無法為具有豐富幾何細節卻缺乏棱角的面部模型創建合適的約束[7,8]。基于深度學習的變形需要大量數據來支撐深度學習算法的訓練,且算法適用領域也和訓練數據相關,相對缺乏普適性[9]。吳越等[10]提出直接利用無三維標簽的二維數據進行三維建模,通過設計弱監督損失函數使其僅根據圖像進行學習;通過縮小渲染人臉與輸入人臉間的差距實現三維重建。微分變形可用于具有豐富幾何細節而表面缺乏棱角的模型重建,但控制點的選擇會影響模型變形效果[11]。張紅穎等[12]提出通過優化變形參數實現面部模型構建,改進位置映射圖網絡獲取更準確特征,以此為基礎定義初始模型參數,再融合回歸方法得到參數來優化模型參數,最后優化變形模型得到最終面部模型。以上各方法都直接在三維空間實現模型構建,更容易發生畸變。
針對以上模型構建方法存在的問題,本文提出基于共形幾何的模型插值構建算法通過引入共形幾何三維變形降維到二維平面;提出多表情模型形狀特征的插值計算來定義過渡表情建模的約束條件;提出自適應模型選擇算法從不同表情的多面部模型中選擇和將生成的過渡模型最接近的面部模型作為建模基礎模型。本文提出的模型構建算法在保證建模效率的同時還提高了表情發生大幅度變化時模型構建的魯棒性,相比于直接在三維空間變形建模更好避免了畸變的發生。
1 基本原理
1.1 問題描述
以現有的多個不同表情三維面部模型為基礎,基于共形幾何插值構建它們的過渡表情,實現表情連續維度的豐富表達。
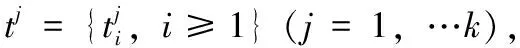
1.2 三維模型配準及特征提取
三維模型配準首先利用Super4PCS[13]算法對不同坐標系下的多個三維面部模型進行粗配準;再通過改進的ICP(iterative closest point)算法對這些三維面部模型進行精配準,將不同坐標系下的多個三維面部模型統一到同一坐標系。具體配準過程如圖1所示。

圖1 三維面部模型配準過程
在三維面部模型的配準過程中,首先將連續維度三維面部模型和面部模板模型依次進行主成分分析,生成累計貢獻率曲線,通過對該曲線配準,獲取每個面部模型和模板面部模型之間的比例因子[14],再將二者歸一化到同一尺度;之后利用Super4PCS[13]算法進行三維面部模型粗配準,在三維面部模板模型中選取同平面的4個頂點作為基點,根據交比一致性在另一三維面部模型中查找和基點對應的四點集的集合,同時求出該三維模型上每一個四點集與基點的變換矩陣;通過比較最大化公共點集,選擇配準精度最高的變換矩陣進行全局變換,實現三維模型粗配準。
將經過粗配準后獲取的旋轉參數和平移參數作為之后基于ICP的精配準初始參數。在原始不同表情面部模型Sn中選取點pi,在原始面部模板模型Q中尋找它的最鄰近點qi,過pi作點法向量ni,過qi作該點的切平面li,此時ni和li的交點為si,查找si的最鄰近點,若鄰近點不變還是qi,則設置|pisi|和|siqi|的邊界閾值,同時剔除該閾值區域之外的所有si點,獲得滿足最小閾值的點對,組成集合Pn和Sn,然后再次計算變換矩陣并根據所計算的變換矩陣和集合Pn,由式(1)得到新的三維頂點集合,同時通過式(2)計算距離diskk+1,當其大于指定閾值時,繼續循環執行以上步驟,直到迭代達到指定次數或disk小于指定閾值,算法停止
(1)
(2)
Rn和Tn分別是第n次迭代后獲取的旋轉變換矩陣和平移變換矩陣,σ為給定的收斂閾值,它的取值會影響模型配準結果的準確性,當滿足distk+1<σ時,三維模型精配準算法結束。配準結果如圖2所示。
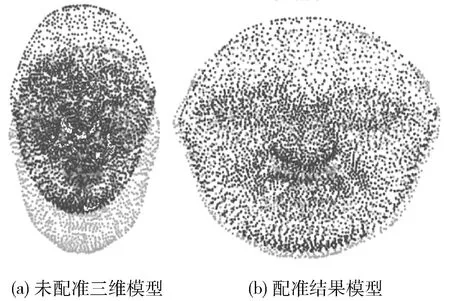
圖2 精配準結果
本文提出利用式(3)表示的配準精度RA來衡量精配準的準確性,配準精度是將模型配準結束時兩個三維模型頂點集合的均方根誤差和模型第一次配準后的兩模型頂點集合均方根誤差相比較來獲取的。表1表示σ的取值對配準精度的影響。可以看到σ=0.001時配準精度接近于1,也就是模型配準結束時兩模型頂點集合的均方根誤差接近于0,即此時配準效果較好
(3)
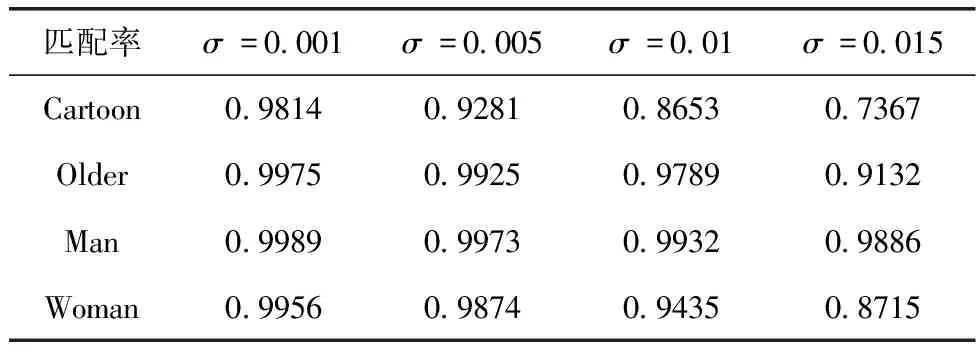
表1 σ的取值對匹配精度的影響
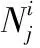
1.3 三維面部模型插值重構
1.3.1 面部模型3D→2D的降維處理
計算共形幾何可以將幾何學問題轉化到工程計算領域。共形映射、準共形映射是共形幾何的研究基礎,在保持局部特征條件下利用解析函數將處于一種空間區域的研究對象映射到另一種空間區域。根據這一理論,共形幾何為三維變形提供一種新思路,將三維空間中的變形操作降維到二維平面。
共形映射、準共形映射研究了在保持局部特征條件下如何在不同空間維度實現共形變換[15]。本文以準共形映射的局部保角性為基礎研究了三維面部模型向二維平面的轉換。

φ*g2=e2λg1
(4)
則此時φ是一個共形雙射,兩張曲面M1和M2共形等價,具有相同的共形不變量。準共形映射是對共形映射的擴展,在實際中應用更廣泛,利用它實現的共形變換雖然從整體上看會存在較大畸變,但卻可以保持了局部特征不變。以此為依據,本文提出了基于準共形映射的從三維空間到二維平面的降維算法。首先計算原始三維面部模型的邊界,記錄邊界點集;其次計算模型邊界線長度與角度,并將模型邊界參數化到圓盤邊界;最后計算模型內部頂點集合的余切拉普拉斯矩陣,并將內部頂點集合參數化到二維圓盤內部。
圖3表達了三維面部模型通過準共形映射從三維空間到二維平面的降維,圖3(a)是一個復雜幾何屬性的三維面部網格模型,圖3(b)是它的降維結果。可以看到經過準共形映射降維后模型的曲率變為零,整體存在了較大畸變,但是眉眼鼻唇的局部細節特征卻得到了完整的保持。
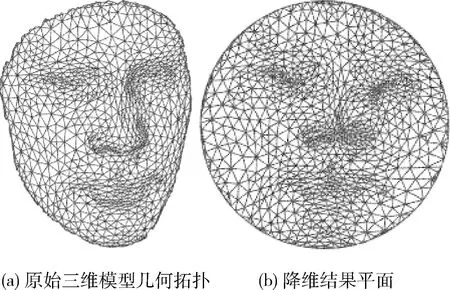
圖3 三維面部模型的降維處理
1.3.2 插值計算過渡模型特征點
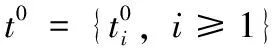
(5)
式中:j代表通過式(5)生成的表情過渡模型索引值,i代表模型中特征點索引值,α代表每個面部模具有的權值,定義了包括模板模型和不同表情連續維度面部模型在內的所有原始模型對將生成的過渡模型的影響,α的定義如式(6)
(6)
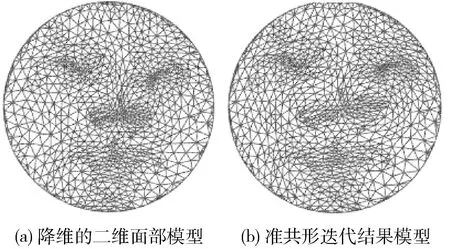
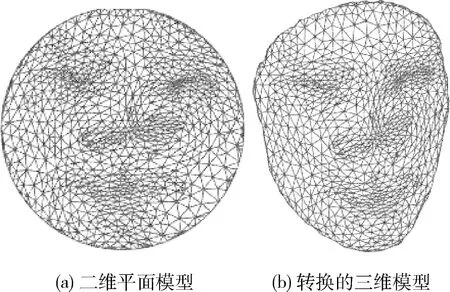
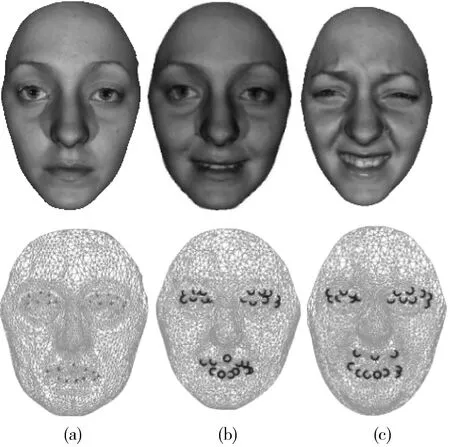
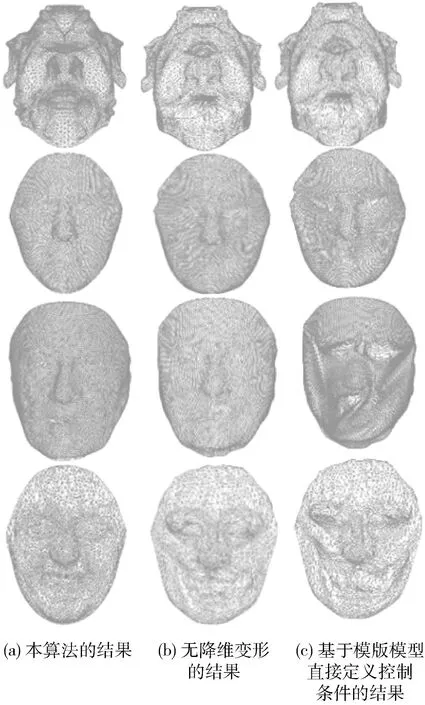
(k-1) 為除模板模型外原始模型數量,di索引值為i的原始模型與模板模型對應特征點中最大距離差。dm為生成的表情過渡模型與面部模板模型的距離,0 1.3.3 自適應定義基礎模型 (7) 1.3.4 面部模型構建 利用式(5)獲取的特征點集合Tj為控制點,引導利用式(7)定義的基礎模型的二維平面準共形迭代,獲取具有過渡表情的面部模型的二維平面數據,具體算法如下: 步驟1 從基礎模型的特征點集合t中選取控制點,利用特征點集合Tj中與選取的控制點對應的頂點,通過式(8)、式(9)計算處理,得到集合t和Tj所包含的對應頂點之間的初始變換關系f0和v0 (8) v0=μ(f0) (9) 其中,μ為貝爾特拉米系數[17];Fb為線性貝爾特拉米求解器[17]。 步驟2 利用基礎模型的網格結構頂點信息vn,通過式(10)~式(12)分別計算μn+1、fn+1和vn+1 (10) (11) (12) 其中,A為拉普拉斯平均算子,δ為參數化到二維平面頂點坐標構成的矩陣。 圖4顯示了準共形迭代處理結果,其中圖4(a)是面部模型降維得到的二維平面,圖4(b)是對二維平面準共形迭代的處理結果。 圖4 準共形迭代的運行結果 將準共形迭代得到的二維模型的拓撲信息和部分頂點的幾何信息為依據,實現模型從二維平面到三維空間的轉換。 首先根據二維模型拓撲信息和幾何信息計算模型的余切拉普拉斯矩陣;然后以一部分頂點為依據定義約束條件;最后引入最小二乘法構建盡可能滿足約束條件的三維模型頂點信息,得到具有過渡表情的三維面部模型。具體算法如下: 步驟1 根據式(13)計算模型的余切拉普拉斯矩陣 (13) 其中,在二維平面中邊 (xi,xj) 會與其它頂點構成三角形,αij和αji是該三角形中與邊 (xi,xj) 相對的角的度數。當 (xi,xj) 為二維平面內部邊時,可以和兩個頂點分別構成兩個三角形,此時就出現兩個 (xi,xj) 邊的對應角,度數分別為αij和αji;而當 (xi,xj) 是邊界邊時,則只能和一個頂點構成三角形,只有一個對應角度數為αij。 步驟2 將三維空間的x、y、z坐標結合余切拉普拉斯矩陣構建線性系統:Wx=0,Wy=0,Wz=0。 步驟3 從非特征點所在區域選擇m個頂點保存到集合C中,C={s1,s2,s3,s4,…sm},每個頂點為Vs=(xs,ys,zs),s∈C,將這m個頂點和步驟2構造的線性方程相結合,構建長度為 (n+m)×n的系統,如式(14)~式(19)所示。其中A的計算由式(15)、式(16)所示 Ax=bx Ay=by Az=bz (14) (15) (16) (17) (18) (19) 步驟4 利用最小二乘法求解滿足如式(20)線性方程的最小值,得到x=(ATA)-1ATbx,y=(ATA)-1ATby,z=(ATA)-1ATbz,則最終所求的頂點坐標為Vnew=(x,y,z) (20) 圖5顯示了模型在不同空間的轉換效果,圖5(a)表示了二維平面模型,圖5(b)表示了利用本方法空間轉換得到的三維面部模型。 圖5 2D→3D模型轉換算法 本文以Matlab為開發工具,以美國紐約州立大學賓漢姆頓分校的BU3DFER三維人臉數據集作為數據源,驗證了所提出的利用插值構建面部模型算法的準確性。 圖6中第一行是原始模型,包括圖6(a)模板模型和連續維度的不同表情模型。本實驗選擇眼睛和嘴巴部分的特征點定義約束條件,插值生成不同表情的過渡模型。圖6第二行顯示了各原始模型中選取的特征點。圖7顯示了本文算法的插值重構結果,其中圖7(a)顯示的是原始模型中滿足差值最小條件的表情模型被降維得到的二維平面,以及在該平面上定義的約束條件,其中圓圈代表來自原始表情模型特征的控制點起始位置,方框代表來自插值后特征點目標位置。其中圖7(b)利用約束條件引導二維模型準共形迭代獲取的結果模型,圖7(c)顯示了通過三維模型恢復算法將圖7(b)表示的模型從二維平面轉換到三維空間,得到的具有過渡表情的三維面部模型。 圖6 原始模型 圖7 重構結果模型 圖8給出了將本文提出的算法應用于不同性別、年齡的面部模型的實驗效果,其中圖8(a)列表示面部模板模型,圖8(b)列和圖8(c)列表示連續維度的不同表情面部模型,圖8(d)列和圖8(e)列是從不同角度展示了利用本算法生成的過渡模型。可以看到圖8(a)~圖8(c)列的眼睛和嘴巴包含了閉合和打開狀態,圖8(d)、圖8(e)顯示的結果模型則在保持眼睛和嘴巴等面部局部細節特征同時面部表情又發生一定變化。 圖8 本文算法的模型插值結果 構建面部這類細節豐富而沒有明顯棱角特征的三維模型時,基于FFD變形或基于骨架變形的重構方法都不適用,所以研究者多選擇使用基于微分變形的重構方法來處理此類模型。表2將本文提出的算法和基于拉普拉斯算子的面部模型重構算法及基于微分坐標的面部模型重構算法的性能進行比較,包括定義約束條件時需要的控制點個數和算法運行時間。可以看到本文算法是在二維空間實現模型變化,所以相較于三維空間的變形,需要的控制點更少,且算法運行時間更短。圖9顯示了3種算法的運行結果,其中圖9(b)是本文算法結果模型,圖9(c)是基于拉普拉斯算子的面部模型重構算法的結果模型,圖9(d)是基于微分坐標的面部模型重構算法的結果模型,可以看出利用他們提出的模型重建算法,直接在三維空間發生形變實現三維模型重建的算法時,對于特征豐富、形變較大的區域,如唇眼部分很容易發生畸變。而本文提出的算法,由于模型變化在二維實現,此時不需要處理深度信息,使重構結果在保持細節的同時產生更少的畸變。 表2 本算法和其它算法的性能比較 圖9 不同模型重構算法處理結果比較 為了驗證該模型構建算法中共形幾何部分和插值構建部分的重要性,將在BU3DFER數據集上進行過渡表情模型構建的消融實驗。消融實驗根據本文提出算法中包含的重要設計分為以下3個部分: (1)本文方法:構建了包含本文提出的基于共形幾何的模型降維處理及基于多模型形狀特征插值生成的模型構建約束條件的完整過渡表情模型構建算法。 (2)對變形算法進行替換,將基于共形幾何的降維變形替換成直接在三維空間進行的微分變形,不再對三維模型進行降維處理,其它結構不變。 (3)對變形基礎模型和變形約束條件進行替換,將利用多模型特征點插值得到的控制約束條件和根據特征點自適應選擇的基礎模型替換為以根據模板模型到某個表情模型特征點距離定義約束條件、以模板模型為基礎模型,其它結構不變。 消融實驗構建過渡表情的面部模型結果如圖10所示。圖10(a)是本文方法得到的建模結果,圖10(b)是將基于共形幾何模型構建方法替換為微分變形的建模結果,圖10(c)是將本文的控制約束條件的定義及自適應選擇基礎模型替換為按單一特征點距離構建約束條件及使用模版模型作為基礎模型的建模結果。相比于圖10(a)本文算法的建模結果,圖10(b)中模型的較大變化區域會出現扭曲,如第一行模型的鼻子、嘴巴和第二行模型的眼睛;而圖10(c)中模型在較大的變形區域內也會出現明顯的畸變,如第三行模型的嘴巴和眼睛出現明顯的扭曲。 圖10 消融算法的定性結果 可以看到,本文提出的模型構建方法的效果是更好的,驗證了共形幾何模塊和插值定義特征點及自適應選擇基礎模型模塊在構建過渡表情面部模型時的重要性,它們都提高了模型變形重構的運行效果。 綜上所述,本文在對模型配準的基礎上通過準共形映射將其降維到二維平面,解決了現有建模方法不易在三維空間構建連續維度多表情模型的問題;然后基于多面部模型特征點插值生成過渡模型特征點并構造控制約束條件;同時根據插值生成的特征點選擇和其距離最小的表情模型,自適應定義變形基礎模型;最后利用控制約束條件引導基礎模型準共形迭代,生成具有過渡表情的面部模型。實驗驗證了本文提出的算法在保持面部模型局部特征的同時很好實現了連續維度多表情模型的構建。在今后的工作中,將進一步研究連續維度不同表情中如果出現大幅度變化表情時配準效果欠佳的問題,并考慮在獲取面部模型特征點時引入深度學習算法,得到更合理的特征點引導面部模型重構。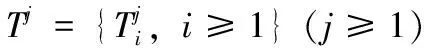




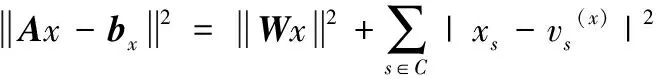
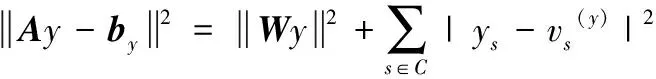
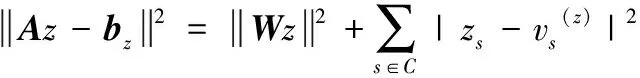
2 分析與討論
2.1 算法運行效果


2.2 傳統模型構建算法效果對比


2.3 消融實驗
3 結束語

