“四畫(huà)”數(shù)學(xué)——構(gòu)建“畫(huà)中有話(huà)”課堂

安徽馬鞍山市含山縣環(huán)峰第二小學(xué)（238100） 肖安群

小學(xué)生的思維以形象為主，數(shù)學(xué)的深層認(rèn)識(shí)卻需要抽象思維，兩者之間就存在“層差”，加上基于小學(xué)數(shù)學(xué)多數(shù)結(jié)論的形成以歸納為主，發(fā)展學(xué)生的邏輯推理能力是一個(gè)大難點(diǎn)。另外，基于數(shù)學(xué)問(wèn)題解決及模型運(yùn)用的需要，學(xué)生要用數(shù)學(xué)信息表達(dá)生活內(nèi)容，但因其綜合度高，小學(xué)生難以完成，需要給小學(xué)生一個(gè)適合的元認(rèn)知策略，以輔助他們完成。這些問(wèn)題可以通過(guò)畫(huà)數(shù)學(xué)這一手段來(lái)解決：把抽象的數(shù)學(xué)具象化，在畫(huà)中厘清結(jié)構(gòu)、洞察關(guān)系、感悟本質(zhì)、提升思維，最終提升學(xué)生的數(shù)學(xué)素養(yǎng)。

一、畫(huà)異同——明白內(nèi)在一致性

（一）畫(huà)出整數(shù)、小數(shù)和分?jǐn)?shù)運(yùn)算的一致性

整數(shù)、小數(shù)和分?jǐn)?shù)的計(jì)算算理有著內(nèi)在統(tǒng)一性，這個(gè)內(nèi)在統(tǒng)一性可以通過(guò)畫(huà)數(shù)學(xué)的方式統(tǒng)一起來(lái)，建立結(jié)構(gòu)化教學(xué)方式。

例如，教學(xué)42÷2 時(shí)，教材是采取“分一分”的方法來(lái)呈現(xiàn)思考過(guò)程的，即先把4 捆小棒（4 個(gè)十）平均分兩份，每份2 捆（2 個(gè)十），再把2 根小棒（2 個(gè)一）平均分兩份，每份1 根（1 個(gè)一），這是按照“十”與“一”兩個(gè)計(jì)量單位上的量的多少進(jìn)行平均分。筆者將教材例題改編為32÷2 和35÷2 進(jìn)行教學(xué)：對(duì)于32÷2，由于3 個(gè)十不能平均分為2 個(gè)整十，要“拆整為零”，在對(duì)2 個(gè)十進(jìn)行平均分后，把剩下的1 個(gè)十拆開(kāi)，與個(gè)位上的2 個(gè)一合為12 個(gè)一后再平均分，這樣把高級(jí)單位降為低級(jí)單位，可以創(chuàng)造繼續(xù)平均分的條件（如圖1）；對(duì)于35÷2，有兩次這樣的降位過(guò)程，第一次是十位余下1 個(gè)十到個(gè)位，第二次是1 個(gè)一余到十分位，這兩次降位，可以利用元和角之間的關(guān)系，用畫(huà)圖策略厘清算理（如圖2）。

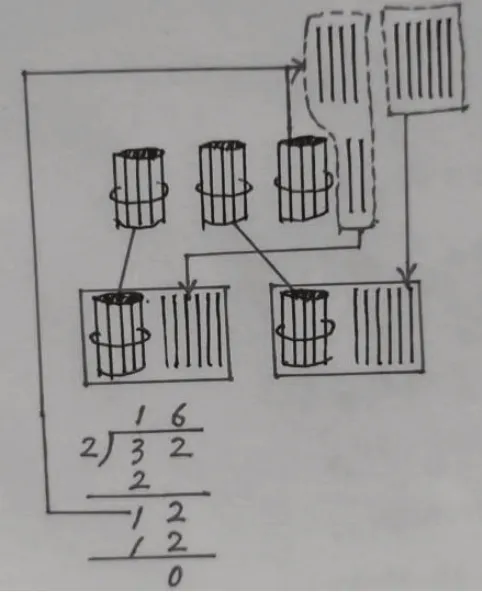
圖1

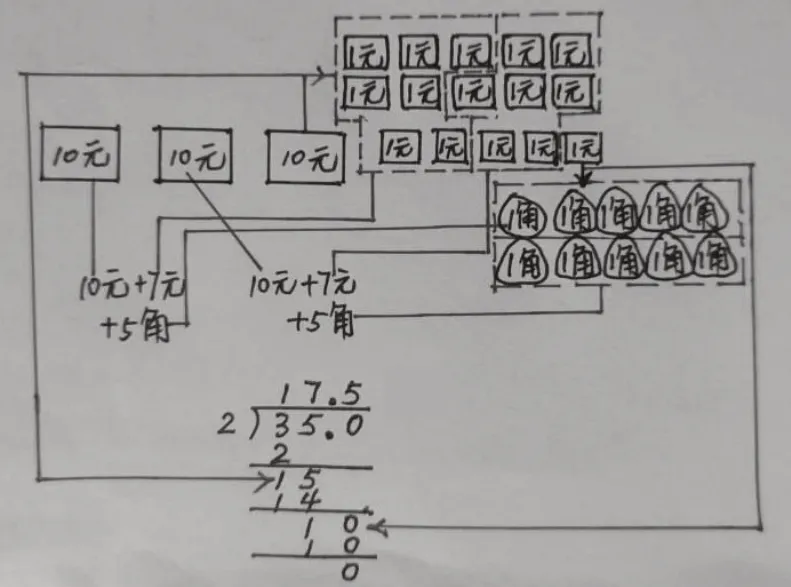
圖2

對(duì)比這3 個(gè)算式的教學(xué)，抓住計(jì)數(shù)單位這個(gè)根本原理，通過(guò)畫(huà)圖，用降位的方式，按計(jì)數(shù)單位逐位平均分，算理上便形成了一致性，使平均分的軌跡得以顯現(xiàn)，計(jì)算背后的道理也得以形象化。

（二）畫(huà)出數(shù)與運(yùn)算的一致性

數(shù)與運(yùn)算是一致的，終極指向都是計(jì)數(shù)單位上的量的多少。例如，教學(xué)9+7 時(shí)，可以從兩個(gè)角度來(lái)理解計(jì)算過(guò)程。首先，“分”與“合”算理的理解，把7分為1和6，其中的1和9合成1個(gè)十，再和剩下的6 個(gè)一合成16，可以通過(guò)圈小棒圖來(lái)理解“滿(mǎn)十進(jìn)1”的道理。其次，是在計(jì)數(shù)器上畫(huà)一畫(huà)，將這一抽象概括的過(guò)程清晰地展示出來(lái)：滿(mǎn)十進(jìn)1 后，這個(gè)1 在十位，表示1 個(gè)十，6 在個(gè)位，表示6 個(gè)一，合起來(lái)是16，這是個(gè)兩位數(shù)，每個(gè)數(shù)位上的位值不同，計(jì)數(shù)單位也就不同。

學(xué)生通過(guò)畫(huà)能夠真正明白：加法計(jì)算時(shí)要“滿(mǎn)十進(jìn)1”，這是計(jì)算的法則，同樣也是計(jì)數(shù)和數(shù)數(shù)的要求，兩者道理是相通的。所以說(shuō)，數(shù)與運(yùn)算具有一致性。

二、畫(huà)思路——悟出本質(zhì)和道理

解決問(wèn)題的方法背后，往往有著深?yuàn)W的道理。通過(guò)畫(huà)數(shù)學(xué)，學(xué)生能將模糊的思維畫(huà)清晰，頓悟相關(guān)條件之間的內(nèi)在聯(lián)系，能透過(guò)表面洞察知識(shí)背后的本質(zhì)。

（一）畫(huà)出數(shù)學(xué)方法背后的道理

例如，在教學(xué)“搭配問(wèn)題”中，用2 件不同的上衣和3 條不同的褲子搭配，共有6 種不同的搭配方式，算式是2×3=6，那為什么算式恰好是2×3=6？直接理解這個(gè)乘法算式的道理對(duì)學(xué)生來(lái)說(shuō)很難，但通過(guò)畫(huà)圖和連線(xiàn)，能讓知識(shí)變得形象（如圖3）。

（二）畫(huà)出數(shù)學(xué)現(xiàn)象背后的本質(zhì)

在探究除法豎式的秘密中，俞正強(qiáng)老師問(wèn)學(xué)生：“加、減、乘法都是把需要計(jì)算的數(shù)寫(xiě)成上下兩排，再畫(huà)一道橫線(xiàn)，最后把結(jié)果寫(xiě)在橫線(xiàn)下面，那為什么除法的結(jié)果是放在算式的最上面？”俞正強(qiáng)老師解釋?zhuān)浩渲械年P(guān)鍵是除法的豎式能有效展現(xiàn)平均分的過(guò)程。為了說(shuō)清這個(gè)道理，俞正強(qiáng)老師正是用畫(huà)數(shù)學(xué)的方式來(lái)解釋。如將6個(gè)桃子平均分給3只小猴，每只小猴拿到幾個(gè)桃子？畫(huà)出的思路如圖4所示：第一行的圖示表示被除數(shù)6，即原來(lái)有6個(gè)桃子；第二行的圖示表示6個(gè)桃子被3只小猴拿走了，每只小猴拿到2個(gè)桃子，即2×3=6；第三行的圖示表示原有的6 個(gè)桃子都被拿走了，剩下0 個(gè)桃子，即6-6=0（個(gè)）。

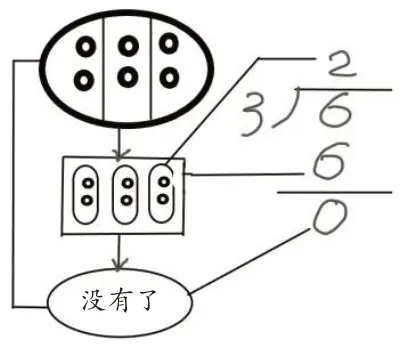
圖4

很少有人去質(zhì)疑除法豎式為什么這樣寫(xiě)，大都認(rèn)為這樣的格式是天然生成的，但若細(xì)問(wèn)成因，則難究其根。而用畫(huà)圖的策略，則能明白過(guò)程、直達(dá)本質(zhì)、答疑解惑。

三、畫(huà)過(guò)程——豐富模型意識(shí)

畫(huà)數(shù)學(xué)的過(guò)程往往會(huì)運(yùn)用到思維模型。學(xué)生會(huì)調(diào)用自己的生活經(jīng)驗(yàn)和模型策略經(jīng)驗(yàn)，不自覺(jué)地將問(wèn)題對(duì)象模型化。以乘法分配律教學(xué)內(nèi)容為例。

師：通過(guò)計(jì)算，我們知道了2×（5+3）和2×5+2×3的結(jié)果相等，它們的結(jié)果為什么相等呢？有什么辦法來(lái)說(shuō)明呢？

生1：我是畫(huà)購(gòu)買(mǎi)筆和練習(xí)本的情況來(lái)理解的（如圖5）。

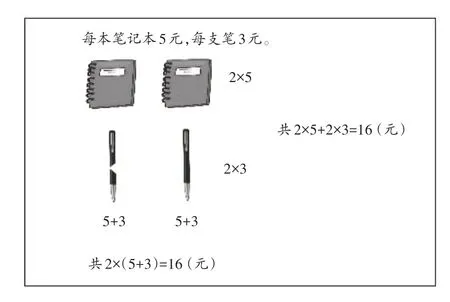
圖5

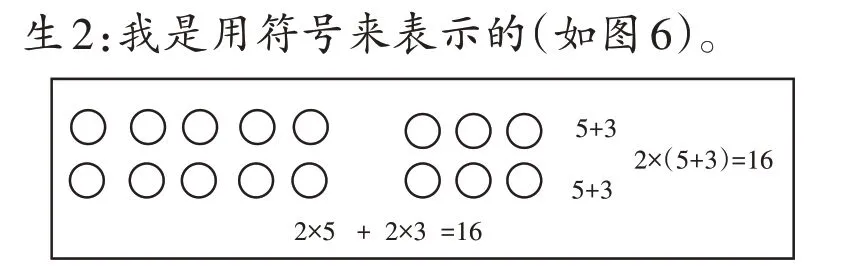
圖6

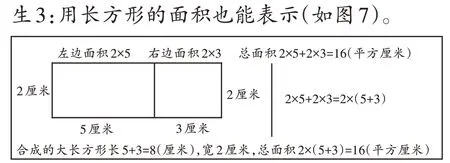
圖7

師：你們畫(huà)得非常棒！對(duì)于算式2×（5+3）=2×5+3，你認(rèn)為對(duì)嗎？又該怎樣說(shuō)明呢？

生4：這個(gè)算式是錯(cuò)的，可以用錢(qián)數(shù)來(lái)說(shuō)明（如圖8）。

圖8

數(shù)學(xué)模型是對(duì)生活原型的概括和提煉，它是以合適的數(shù)學(xué)符號(hào)和數(shù)學(xué)語(yǔ)言，精準(zhǔn)表達(dá)事物的特征、相互關(guān)系和存在的規(guī)律。數(shù)學(xué)學(xué)習(xí)的基本過(guò)程之一就是自主建立數(shù)學(xué)模型，對(duì)小學(xué)生來(lái)說(shuō)，依據(jù)生活經(jīng)驗(yàn)和模型經(jīng)驗(yàn)，由具體的情境素材提煉成抽象的數(shù)學(xué)模型，再經(jīng)歷畫(huà)的過(guò)程，可使原先堵塞的環(huán)節(jié)被打通，學(xué)習(xí)思路豁然開(kāi)朗。

四、畫(huà)重點(diǎn)——形成高階思維

日本數(shù)學(xué)家米山國(guó)藏認(rèn)為，學(xué)生所學(xué)的數(shù)學(xué)知識(shí)，在進(jìn)入社會(huì)后幾乎沒(méi)有什么機(jī)會(huì)應(yīng)用，因而這種作為知識(shí)的數(shù)學(xué)，出校門(mén)不到兩年就忘了，唯有深深銘記在頭腦中的數(shù)學(xué)思想和方法等隨時(shí)發(fā)揮作用，使他們終身受益。然而在實(shí)際教學(xué)中，多數(shù)教師都有這樣的苦惱：用怎樣的方式才能有效促使學(xué)生擁有深刻的數(shù)學(xué)思維呢？研究表明，后天的經(jīng)歷和學(xué)習(xí)對(duì)思維的提升有很大的幫助。針對(duì)小學(xué)生的年齡特征，畫(huà)數(shù)學(xué)可以有效地提升學(xué)生的思維層次。

（一）經(jīng)歷畫(huà)的過(guò)程，讓探究深一些

教學(xué)要求學(xué)生畫(huà)出圓柱（如圖9-1）的展開(kāi)圖。

圖9-1

生1：這個(gè)圓柱的展開(kāi)圖是1個(gè)正方形和2個(gè)圓。

生2：不對(duì)，這個(gè)圓柱的展開(kāi)圖是1個(gè)長(zhǎng)方形和2個(gè)圓。

生3：這個(gè)圓柱的展開(kāi)圖是1 個(gè)長(zhǎng)方形和2 個(gè)圓，長(zhǎng)方形的長(zhǎng)等于圓的周長(zhǎng)（πd），長(zhǎng)方形的寬等于圓柱的高。由于長(zhǎng)方形的長(zhǎng)比圓的直徑的3 倍多一些，所以我畫(huà)的圖示中長(zhǎng)方形的長(zhǎng)比圓的3 段直徑的長(zhǎng)度長(zhǎng)一些（如圖9-2）。

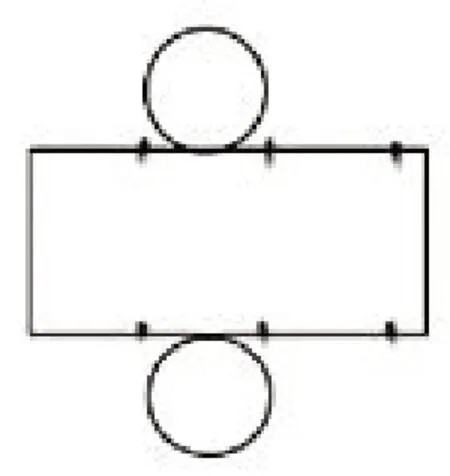
圖9-2

生1 只感受到展開(kāi)圖的大致形狀，卻把握不住展開(kāi)圖與立體圖形之間的內(nèi)在聯(lián)系；生2 能夠修正生1的錯(cuò)誤，知道展開(kāi)圖的長(zhǎng)不是對(duì)應(yīng)著直徑；生3在畫(huà)圖中，能將長(zhǎng)方形的長(zhǎng)準(zhǔn)確對(duì)應(yīng)圓的直徑的3倍多一些的關(guān)系，思維層級(jí)明顯上升。這樣的作圖分析過(guò)程，能讓學(xué)生把抽象的對(duì)應(yīng)關(guān)系在具體的圖示中顯現(xiàn)出來(lái)，助力思維的提升。

（二）經(jīng)歷畫(huà)的過(guò)程，讓算理淺顯易懂

隔位退位減法是教學(xué)的一大難點(diǎn)，學(xué)生難以理解借1的必要性和借1的方法。以“201-186”為例，筆者和學(xué)生共同畫(huà)圖（如圖10-1）。結(jié)合圖示，筆者組織學(xué)生進(jìn)一步討論：201-186 的豎式中有兩個(gè)退位點(diǎn)，這兩個(gè)退位點(diǎn)在圖示中的哪里？基于討論，筆者和學(xué)生繼續(xù)完善圖示（如圖10-2）。

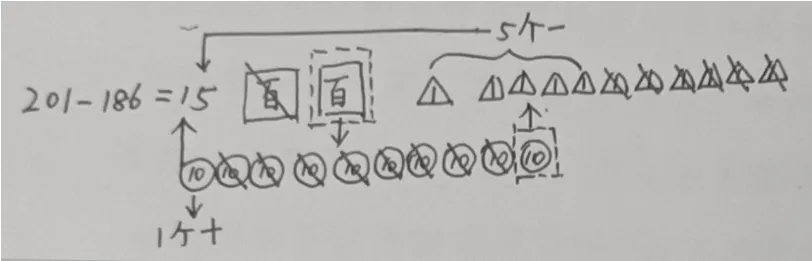
圖10-1

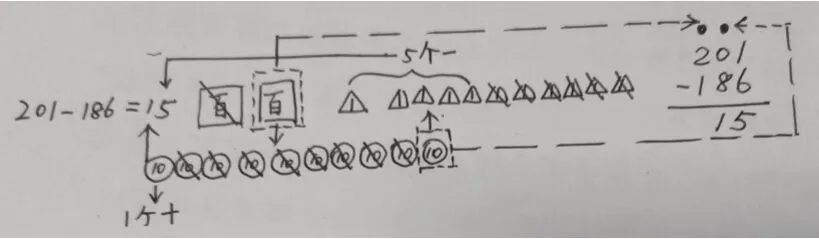
圖10-2

通過(guò)這個(gè)完善過(guò)程，將抽象的退位對(duì)應(yīng)關(guān)系用流程圖表達(dá)出來(lái)，用形的變化表達(dá)數(shù)的變化過(guò)程，把問(wèn)題的本質(zhì)形象地展示出來(lái)，使抽象的算理與圖的軌跡一一對(duì)應(yīng)，讓算理變得淺顯易懂。

（三）經(jīng)歷畫(huà)的過(guò)程，讓思維轉(zhuǎn)向

數(shù)與形的對(duì)應(yīng)，還可以設(shè)計(jì)為逆向思考形式。例如，教學(xué)折線(xiàn)統(tǒng)計(jì)圖后，讓學(xué)生將原龜兔賽跑故事以及將故事新編設(shè)計(jì)成折線(xiàn)圖（實(shí)線(xiàn)表示烏龜?shù)倪\(yùn)動(dòng)軌跡，虛線(xiàn)表示兔子的運(yùn)動(dòng)軌跡）。

生1：我是按原故事來(lái)畫(huà)折線(xiàn)圖的，烏龜最終贏得了比賽（如圖11-1）。

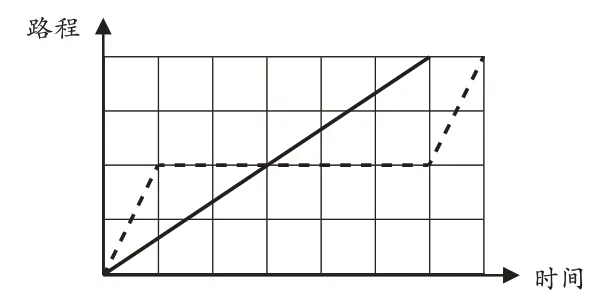
圖11-1

生2：我將故事進(jìn)行新編，兔子雖然偷懶了，但它乘勝追擊，最終兩者同時(shí)到達(dá)終點(diǎn)（如圖11-2）。

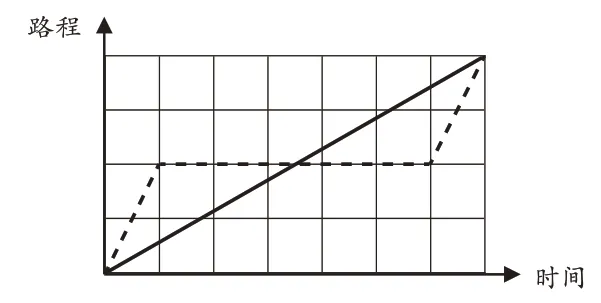
圖11-2

生3：我也將故事進(jìn)行新編，兔子沒(méi)有偷懶，迅速到達(dá)了終點(diǎn)。當(dāng)然，烏龜很有毅力，最終也堅(jiān)持到達(dá)了終點(diǎn)（如圖11-3）。

從讓學(xué)生看圖說(shuō)意到畫(huà)圖表意，開(kāi)放性的教學(xué)讓學(xué)生的思維更廣闊、創(chuàng)新點(diǎn)更多、思維層級(jí)更高。

（四）經(jīng)歷畫(huà)的過(guò)程，學(xué)會(huì)推導(dǎo)結(jié)論

部分教師在教學(xué)3 的倍數(shù)的特征時(shí)，讓學(xué)生在百數(shù)表中通過(guò)猜想和歸納得出結(jié)論后，就結(jié)束探究活動(dòng)，迅速進(jìn)入應(yīng)用練習(xí)環(huán)節(jié)，原因是這部分教師認(rèn)為這個(gè)特征只能用中學(xué)代數(shù)知識(shí)來(lái)證明，小學(xué)生推導(dǎo)起來(lái)難度太大。

筆者在教學(xué)這一課時(shí)，運(yùn)用畫(huà)圖的策略，將每個(gè)數(shù)位上的算珠3 個(gè)3 個(gè)地圈起來(lái)后，在余下的算珠中找到了“數(shù)字和”，用畫(huà)圖支持了“數(shù)字和”的判斷結(jié)論，打破了小學(xué)生不能講清數(shù)字和道理的論斷。

經(jīng)歷畫(huà)的過(guò)程、看形想數(shù)，學(xué)生能進(jìn)一步明確對(duì)應(yīng)關(guān)系，找到數(shù)量關(guān)系的聯(lián)結(jié)點(diǎn)，讓條件之間的隱形對(duì)應(yīng)關(guān)系顯性化，提升思維層級(jí)。畫(huà)數(shù)學(xué)，如同一臺(tái)“X 光機(jī)”，讓看不見(jiàn)的深層理論關(guān)系浮出水面，凸顯成像。

孔凡哲認(rèn)為，數(shù)學(xué)認(rèn)知結(jié)構(gòu)是有主觀(guān)能動(dòng)性的組織，人形成一定的數(shù)學(xué)認(rèn)知結(jié)構(gòu)后，一旦出現(xiàn)新的數(shù)學(xué)信息，就會(huì)立即用相應(yīng)的數(shù)學(xué)認(rèn)知結(jié)構(gòu)對(duì)所面臨的信息進(jìn)行加工處理，從而表現(xiàn)出數(shù)學(xué)認(rèn)知結(jié)構(gòu)的能動(dòng)性，其中，同化和順應(yīng)是學(xué)生原有數(shù)學(xué)認(rèn)知結(jié)構(gòu)和新的學(xué)習(xí)內(nèi)容相互作用的兩種基本形式。而畫(huà)出思維的過(guò)程，特別容易實(shí)現(xiàn)這種同化和順應(yīng)（如圖12）。

圖12

綜上所述，畫(huà)出數(shù)學(xué)學(xué)習(xí)的過(guò)程，打開(kāi)數(shù)學(xué)思考的大門(mén)，就是為思維搭梯子，為方法找鑰匙，為拓展開(kāi)窗戶(hù)。由圖出發(fā)，不止于圖，圖思結(jié)合，螺旋上升，走向抽象和邏輯推理，數(shù)學(xué)學(xué)習(xí)將會(huì)變得無(wú)比有趣。