長期擬周期近直線暈軌道高效設(shè)計方法

秦理民，楊洪偉，李 爽

（南京航空航天大學(xué)航天學(xué)院，南京 211106）

0 引言

NASA 的阿爾忒彌斯（Artemis）項目［1］計劃將人類重新帶回月球，使得目前國際上對于近月空間的探索成為了新的重點。同時，一個被稱為月球網(wǎng)關(guān)［2］的新型空間站將被放置在月球軌道上，近月空間站建設(shè)可以大大提高人類對深空探測的長期探索能力，包含太陽系其他行星和小行星探測任務(wù)。未來我國也將進(jìn)入對地月空間大規(guī)模開發(fā)與探索的新階段以及進(jìn)行新的深空探測任務(wù)［3-4］。

月球空間站的計劃軌道之一是近直線暈軌道（Near rectilinear Halo orbit，NRHO）［2］，它是地月共線平動點halo 軌道的一個子族［5］。在圓型限制性三體問題（Circular restricted three-body problem，CRTBP）中NRHO 被確認(rèn)是在月球附近有良好穩(wěn)定性的周期軌道族，且這一軌道族相比于halo 軌道的其余部分有更低的近月點半徑。NASA 目前選定的月球網(wǎng)關(guān)軌道為L2 點南族9∶2 會合共振NRHO［2］，文獻(xiàn)［6］中分析了NRHO 作為月球空間站的適用性。近年來，NRHO 與halo 軌道在地月空間的轉(zhuǎn)移任務(wù)也得到了廣泛的研究［7-9］。

不同動力學(xué)模型下會合共振NRHO 的研究受到廣泛關(guān)注，Boudad 等［10］分析了會合共振NRHO 在雙圓限制性四體問題下對應(yīng)周期軌道的動力學(xué)特性。Villegas-pinto 等［11］在考慮月球偏心率和太陽引力的橢圓-圓限制性四體問題下分析共振擬周期NRHO。此外，Zimovan-spreen 等［12］對NRHO 和其周圍的高倍周期分岔軌道族的動力學(xué)特性進(jìn)行了分析。這些研究都表明，會合共振NRHO 在多種動力學(xué)模型下有效保留了避免月球和地球遮擋以及近線性穩(wěn)定的動力學(xué)特性。

但是，在高精度的星歷模型下，NRHO 將演變?yōu)閿M周期軌道。文獻(xiàn)［13］中給出了圓型限制性三體問題下大幅值擬周期軌道的數(shù)值計算方法，但未考慮多攝動影響下的高精度模型。利用數(shù)值方法在高精度星歷模型下構(gòu)造擬周期軌道，包含二級微分修正方法［14-15］和多點打靶法［16-17］。但這些研究多關(guān)注于平動點周圍的halo軌道和Lissajous軌道且往往只計算了少圈次的擬周期軌道［14-17］。目前對于在高精度模型下的NRHO 維持和導(dǎo)航已有相關(guān)研究分析［18-20］，其結(jié)果驗證了在真實星歷模型下維持?jǐn)MNRHO 運動的可行性。雖然其中也有提及長期擬周期NRHO 的生成過程，但其中計算初始多圈次擬周期NRHO 包含了數(shù)值敏感區(qū)域的離散點，增加了多點打靶的求解難度。Williams 等［18］提出了滾動時域方法計算長期擬周期NRHO，但其中只提到從一個良好收斂的初始解開始可以保證滾動時域方法計算長期軌道的有效性，并未明確指出不同NRHO 初始生成解對于長期擬周期NRHO 計算的影響，同時并未給出滾動時域算法中具體的修正策略。且目前多關(guān)注于L2點南族NRHO［18-20］，缺少對于L2點北族和L1點NRHO的適用性分析。

為此，針對現(xiàn)有的長期擬周期NRHO 數(shù)值計算方法存在的不足，本文提出了新的離散點選取策略，提高了多點打靶法計算多圈次擬周期NRHO 的收斂性能并能有效降低迭代打靶所需的計算時間。進(jìn)一步利用NRHO 的對稱性給出了初始擬周期NRHO 圈次延續(xù)方法和滾動時域長期擬周期NRHO生成方法，同時提出依賴擬周期軌道近月點半徑判斷的修正策略，以保證滾動時域方法的可延續(xù)性和更少的迭代修正次數(shù)。在仿真算例中，本文將對地月L2 點NRHO 和L1 點NRHO 進(jìn)行分析，評估擬周期NRHO 的近月點半徑振蕩對長期生成的影響，以及長期擬周期NRHO生成方法的有效性。

1 動力學(xué)建模與軌道選取

1.1 圓型限制性三體問題

圓型限制性三體問題通常在會合坐標(biāo)系下描述航天器的運動，航天器的狀態(tài)量為，其中rsyn和vsyn分別為航天器在會合坐標(biāo)系下的位置和速度，其動力學(xué)方程為［21］：

其中，U代表系統(tǒng)的偽勢能：

式中：μ為系統(tǒng)的質(zhì)量參數(shù)；r1和r2分別為航天器相對于地球和月球的距離：

1.2 高精度星歷模型

高精度星歷模型很好地描述了航天器在多天體引力下的運動，此模型建立在以行星為中心的J2000 慣性系下，天體的位置和速度通過讀取NASA的導(dǎo)航和輔助信息設(shè)施（NAIF）提供的SPICE 星歷數(shù)據(jù)庫［22］獲得。

以地球為中心天體，航天器的狀態(tài)量為X=其中r和v分別為航天器在慣性系下的位置和速度，航天器在多個天體引力作用下的動力學(xué)方程為：

式中：G為萬有引力常數(shù)；me為地球質(zhì)量；mi和ri分別為月球、太陽以及其他星體的質(zhì)量和位置矢量。

定義瞬時歸一化長度單位l*、時間單位t*和速度單位v*為

則航天器在地球J2000 慣性系下的狀態(tài)量rin和vin轉(zhuǎn)換為歸一化的瞬時地月會合系下的位置和速度：

式（7）中rsyn，e=[-μ，0，0]T為瞬時地月會合坐標(biāo)系下地球的位置坐標(biāo)。通過上述轉(zhuǎn)換的逆過程可將航天器在地月會合坐標(biāo)系下的坐標(biāo)轉(zhuǎn)移至地球J2000慣性系下。

1.3 軌道選取

NRHO 是月球附近具有良好穩(wěn)定性的周期軌道族，它被認(rèn)為是月球門戶和月球空間站建設(shè)的重要潛在應(yīng)用軌道。地球-月球-太陽的會合周期為29.5 天，文獻(xiàn)［10-12］論證了會合共振NRHO 能有效避免月球和地球遮擋。本文所選取的NRHO 參數(shù)如表1所示，所對應(yīng)的軌道分別為L2點9∶2共振、L2 點4∶1 共振和L1 點11∶3 共振。表中NRHO 的狀態(tài)量以會合坐標(biāo)系下的無量綱單位表示。

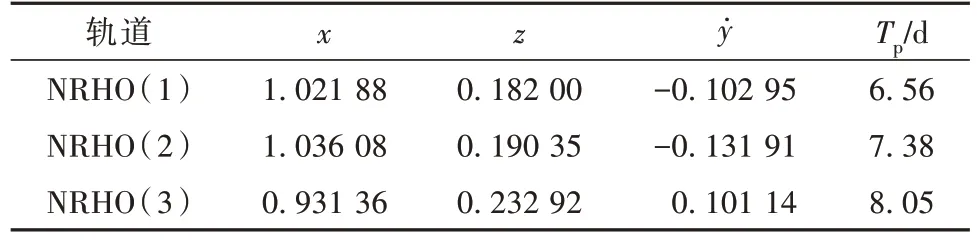
表1 所選NRHO的軌道參數(shù)Table 1 Orbital characteristics of the selected NRHOs

2 長期擬周期NRHO生成方法

雖然NRHO 在圓型限制性三體問題下表現(xiàn)出良好的穩(wěn)定性，但在真實情況下，受到月球偏心率和其他天體引力的影響，擬周期NRHO 在一定圈次后即發(fā)散。但生成長期的擬周期NRHO 標(biāo)稱軌跡是軌道保持的關(guān)鍵，故本小節(jié)給出了三級修正的長期擬周期NRHO設(shè)計方法。

1）第一級修正：從圓型限制性三體問題轉(zhuǎn)到高精度星歷模型。

以圓型限制性三體問題下生成的NRHO 作為初始猜測，利用多點打靶法［16］構(gòu)造擬周期NRHO。此過程的自由變量為各個離散點的狀態(tài)量Xq(q=1，…，M)：

為保證軌道的連續(xù)性，約束表示為

約束變量F1對于自由變量C1的雅可比矩陣為

式中：Φ為6 × 6的狀態(tài)轉(zhuǎn)移矩陣；I表示單位矩陣。

由于自由變量C1與約束變量F1的維度不相等，故使用最小范數(shù)解對自由變量進(jìn)行迭代更新：

式中：K=0，1，2，…為迭代次數(shù)。

本文考慮到月球附近離散點對參數(shù)的敏感性，提出了離散點刪除策略，對初始離散點選取進(jìn)行改進(jìn)，提高多點打靶過程對于多圈次擬周期NRHO 的收斂性。首先考慮將每圈次的NRHO 等時間離散為10 段，然后通過x軸坐標(biāo)逐步刪除靠近近月點位置的離散點，離散點選取方案示意圖如圖1 所示。

圖1 離散點選取示意圖Fig.1 Schematic diagram of discrete point selection

2）第二級修正：初始擬周期NRHO圈次延續(xù)。

為延續(xù)第一級修正獲得的擬NRHO 圈次，第二級修正利用圓型限制性三體問題下NRHO 的對稱特性，即NRHO 每次通過近月點位置時=0（此速度為在地月會合坐標(biāo)系下的速度），以第一級修正獲得的NRHO 作為初始解，通過修正X0使N圈次后的近月點速度滿足對稱性條件。此過程的自由變量為初始的三軸速度量：

約束為N圈次后近月點的x軸速度，表示為：

N圈次后的近月點在會合坐標(biāo)系下的速度vsyn，p，N對于自由變量C2的偏導(dǎo)數(shù)為：

式中：Φi，j為狀態(tài)轉(zhuǎn)移矩陣Φ中的元素；Rt，和分別為末端近月點時刻所對應(yīng)的旋轉(zhuǎn)矩陣、角速度矩陣和瞬時歸一化速度單位；Q為3 × 3的矩陣。

約束變量F2對于自由變量C2的雅可比矩陣為：

式中：下標(biāo)i，j為Q中對應(yīng)元素的位置。同樣使用最小范數(shù)解對自由變量C2進(jìn)行更新：

通過該修正過程可以獲得N圈次下擬穩(wěn)定的軌跡，將該軌跡延續(xù)至N+1 圈次，進(jìn)一步修正初始速度即可獲得N+1 圈次的擬周期NRHO 軌跡，重復(fù)上述過程以延續(xù)初始擬周期NRHO圈次。

3）第三級修正：滾動時域方法生成長期擬周期NRHO。

當(dāng)獲得理想圈次的擬周期NRHO 軌跡后，采用滾動時域方法計算長期擬周期NRHO。滾動時域方法開始于初始近月點Xp，0，其向前積分N圈次到新的近月點Xp，N，通過修正初始近月點的速度使=0。然后將修正后得到的初始近月點向前積分到下一個近月點Xp，1，重復(fù)上述過程直到獲得理想圈次的軌跡。

由此，第三級修正的自由變量為k圈次時的近月點的三軸速度量：

約束為k+N圈次后的x軸速度，表示為

約束變量F3對于自由變量C3的雅可比矩陣同式（16）。

然而，近月點速度的修正只能保證后續(xù)N圈次是擬穩(wěn)定的，同時會導(dǎo)致N圈次后近月點位置和歷元時刻的改變，只包含一次修正的滾動時域方法對部分NRHO 會在一定圈次后發(fā)散。對近月點速度的多次修正可以解決軌跡發(fā)散的問題，但多次修正意味著計算量的成倍增加。本文引入當(dāng)前修正N+1圈次后近月點半徑Rp，k+N+1的約束來對后續(xù)發(fā)散程度較大的近月點Xp，k進(jìn)行多次修正來保證算法的收斂性，同時避免不必要修正所帶來的計算量的增加。設(shè)置允許的最大近月點半徑Rp，max和最小近月點半徑Rp，min，根據(jù)其發(fā)散特性給出了如下不同的修正策略：

1）Rp，k+N+1＞Rp，max。

此情況下N+1 圈次后的軌跡已存在較大發(fā)散，首先通過多次修正Xp，k使N圈次后近月點滿足式（19）來減小Rp，k+N+1，同時設(shè)置最大修正迭代次數(shù)nit-max1。若多次修正后Rp，k+N+1仍不滿足約束，則多次修正Xp，k使N+1 圈次后近月點滿足式（19），同時設(shè)置最大修正迭代次數(shù)nit-max2。

2）Rp，k+N+1＜Rp，min。

此情況表明N+1 圈次內(nèi)的軌跡沒有發(fā)散，但近月點的降低會導(dǎo)致N+2 圈次后的軌跡發(fā)散而使?jié)L動時域方法失敗。此時通過多次修正Xp，k使N+1 圈次后近月點滿足式（19）來抬升Rp，k+N+1，同時設(shè)置最大修正迭代次數(shù)nit-max3。

多數(shù)圈次在增加一次修正后可以滿足近月點半徑要求。但由于在真實星歷模型下，擬周期NRHO 近月點半徑發(fā)生振蕩的動力學(xué)特性，對于初始近月點狀態(tài)的多次修正可能也無法使多圈次后的近月點半徑滿足約束，故需設(shè)置最大修正迭代次數(shù)以結(jié)束修正，滾動時域方法流程圖如圖2 所示。綜上所述，長期擬周期NRHO 生成方法圖解如圖3所示。

圖2 滾動時域方法中修正策略流程圖Fig.2 Flow chat of correction strategy in the receding horizon method

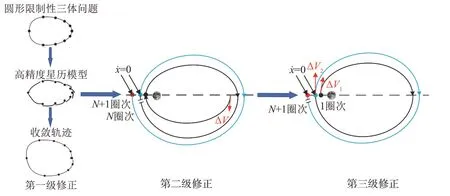
圖3 長期擬周期NRHO生成方法圖解Fig.3 Diagram of long-term quasi-NRHO generation method

3 仿真試驗和結(jié)果分析

仿真以1.3 節(jié)所選取的NRHO 為例計算擬周期NRHO。起始時間為“2025.01.01.000 UTD”，考慮日地月木四天體引力作用下的高精度星歷模型。

3.1 第一級修正算例分析

所選目標(biāo)軌道在第一級修正過程中離散點選取與收斂圈次的比較如表2 所示。此結(jié)果表明，減少單圈次離散點的策略能有效增加多點打靶法的收斂圈次。同時該策略能有效減少迭代次數(shù)和計算時間，對于計算三圈擬周期NRHO（1）收斂軌跡，使用MATLAB 中的ode 45 積分器進(jìn)行軌道積分，絕對誤差和相對誤差分別設(shè)置為1×10-14和1×10-12。采用單圈次5個離散點的策略求解時間和迭代次數(shù)分別為13.191 s 和6 次，而采用單圈次10 個離散點則需要48.898 s和19次迭代。

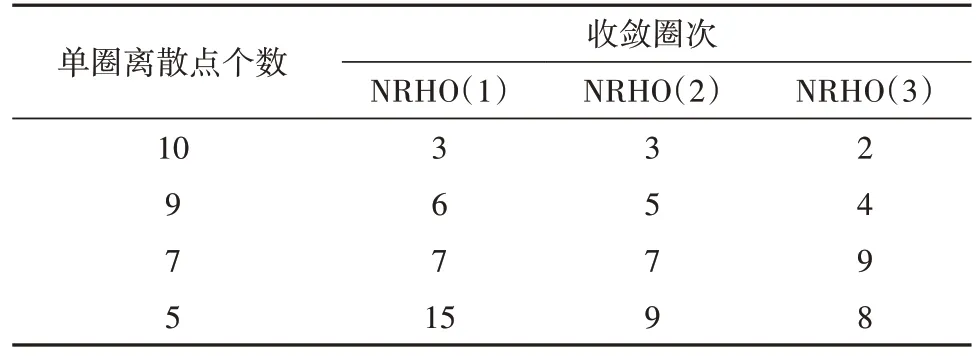
表2 離散點選取與收斂圈次的比較Table 2 Comparison of discrete point selection and converged revolutions

以NRHO（1）為例的第一級修正收斂解如圖4所示，此結(jié)果繪制在歸一化的地月會合坐標(biāo)系下，虛線軌跡為NRHO，圓點對應(yīng)不同收斂解下所選取的離散點，實線軌跡為擬周期NRHO。

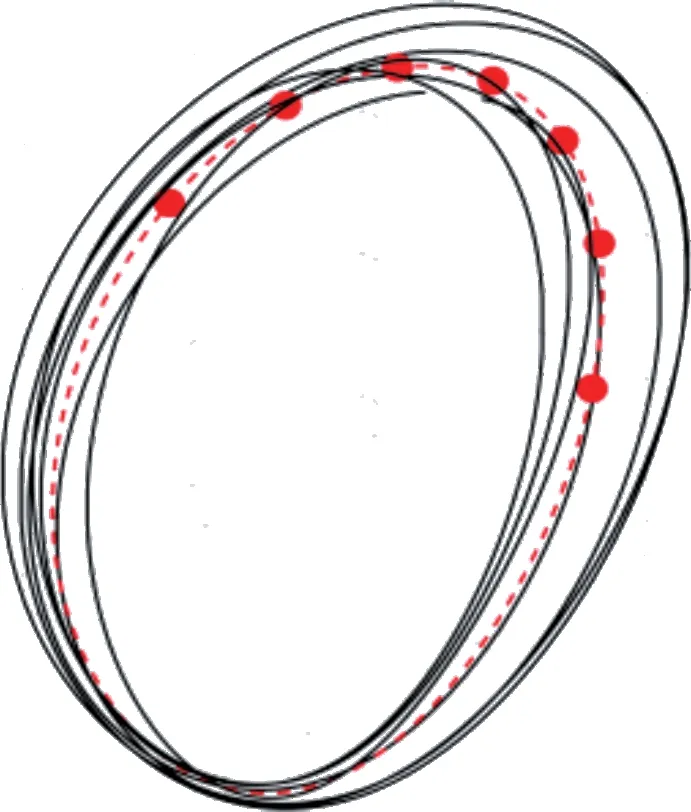
圖4 NRHO（1）第一級修正收斂解Fig.4 Converged solutions for the first-level correction of NRHO（1）

3.2 第二級修正算例分析

雖然第一級修正給出的離散點選擇策略能有效增加多圈次擬周期NRHO的收斂性能，但由于刪除近月點周圍離散點導(dǎo)致NRHO部分信息的缺失，有可能導(dǎo)致擬周期NRHO近月點漂移。第二級修正可以有效解決這一問題，選擇圈次較少但近月點偏離較少的收斂解進(jìn)行延續(xù)可以很好地保證近月點半徑的變化范圍。對于NRHO（1），選擇10 圈收斂解和選擇15 圈收斂解生成維持21 圈軌跡的近月點半徑變化如圖5（a）所示；對于NRHO（2），選擇7圈收斂解和選擇9圈收斂解生成維持18圈軌跡的近月點半徑變化如圖5（b）所示。此結(jié)果表明，第二級修正策略維持了近月點半徑更小幅度的變化。與此同時，近月點半徑更少的偏移也保證了第三級修正過程不易發(fā)散。

圖5 不同初始解下近月點半徑變化Fig.5 The change of perilune radius with different initial solutions

從上述第一級修正中選擇合適圈次的擬周期NRHO收斂解作為初始值，利用第二級修正方法延續(xù)擬周期NRHO 圈次，最終生成維持22 圈140 天的擬周期NRHO（1）軌跡、24圈170天的擬周期NRHO（2）軌跡和14 圈110 天的擬周期NRHO（3）軌跡如圖6所示，實線軌跡為擬周期NRHO，圓點為月球。上述結(jié)果表明，第二級修正能有效彌補(bǔ)第一級修正收斂圈次的不足，生成更多圈次的擬周期NRHO。

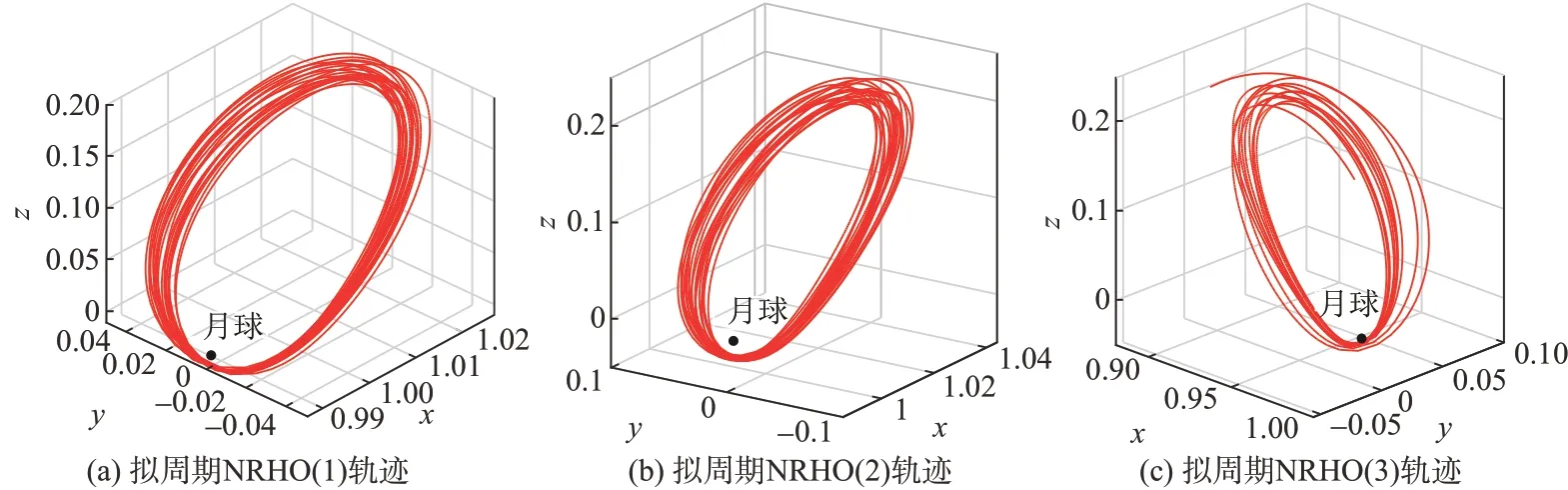
圖6 NRHOs第二級修正收斂解Fig.6 Converged solutions for the second-level correction of NRHOs

3.3 第三級修正算例分析

生成了足夠圈次的初始擬周期NRHO，利用第三級修正滾動時域方法進(jìn)行長期擬周期NRHO 計算。為驗證本文中所提出的修正策略的有效性，同時利用單次修正、多次修正和本文修正策略對滾動時域方法可生成圈次進(jìn)行了比較。其中單次修正指只對Xp，k進(jìn)行一次修正使N圈次后近月點滿足式（19）；多次修正是指對Xp，k進(jìn)行一次或二次修正使N圈次后近月點滿足式（19），再對Xp，k進(jìn)行一次修正使N+1圈次后近月點滿足式（19）（當(dāng)有一種情況不發(fā)散時即停止）。分別對3.2 節(jié)中初始10 圈延續(xù)得到的擬周期NRHO（1）、初始7圈延續(xù)得到的擬周期NRHO（2）和初始9 圈延續(xù)得到的擬周期NRHO（2）進(jìn)行了長期計算，其結(jié)果如表3所示。

表3 不同修正策略下滾動時域方法性能對比Table 3 Performance comparison of the receding-horizon method with different correction strategies.

由上述結(jié)果可以看出，對于L2 點9：2 會合共振的NRHO（1）來說，單次修正即可保證軌跡不會發(fā)散。而對于4∶1 共振的NRHO（2），即使選取了近月點漂移較少的第二級修正收斂解，單次修正依然會在少圈次后發(fā)散。這樣的結(jié)果同時表明了9：2會合共振軌道作為網(wǎng)關(guān)軌道更好的適用性。對于近月點半徑漂移較少的擬周期NRHO（2），多次修正可以保證軌跡不發(fā)散，但至少需要在每圈次近月點實施3 次修正計算，這意味著計算500 圈的長期擬周期軌道需要1 500 次迭代修正過程，而本文提出策略則只需要1 040 次，可大幅度減少迭代次數(shù)，提高計算效率。在利用滾動時域方法計算近月點半徑漂移較大的擬周期NRHO（2）的長期結(jié)果時，多次修正策略仍會失敗，這是因為當(dāng)Rp，k+N+1＜Rp，min時，對N圈后近月點的修正會使N+1圈次后的近月點半徑Rp，k+N+1進(jìn)一步降低從而導(dǎo)致后續(xù)軌跡的發(fā)散，而根據(jù)近月點半徑判斷的本文策略仍可以延續(xù)至所需圈次。

除此之外，本文提出的依賴近月點半徑的修正策略因為約束了近月點半徑，確保了多數(shù)圈次內(nèi)擬周期NRHO 近月點的振蕩范圍，使擬周期NRHO 的軌道特性更接近圓型限制性三體問題中的NRHO。

最終生成維持500圈約10年的擬周期NRHO 如圖7 所示，實線軌跡為擬周期NRHO，圓點為月球。對于NRHO（1）選擇N=12維持500圈所需的速度增量為58.55 mm/s，近月點處最大脈沖為0.358 9 mm/s。對于NRHO（2）選擇N=10維持500圈所需的速度增量為29.65 mm/s，近月點處最大脈沖為0.291 2 mm/s。此結(jié)果比以往研究中L2點南族NRHO維持500圈次所需速度增量更小［18］，說明了本文方法的有效性，同時可能說明L2 點北族擬周期NRHO 具有比L2 點南族擬周期NRHO 更接近圓型限制性三體問題下NRHO的軌道特性。

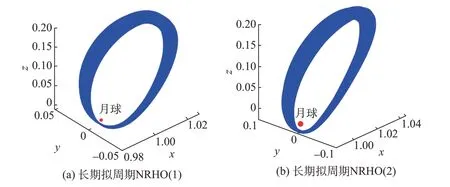
圖7 長期擬周期NRHOsFig.7 Long-term quasi-periodic NRHOs

4 結(jié)論

本文針對地月空間中高精度星歷模型下長期擬周期NRHO 設(shè)計問題，給出了一種新型三級修正策略的長期擬周期NRHO 設(shè)計方法，對L1 和L2 點的NRHO 進(jìn)行了仿真計算。計算結(jié)果表明，提出的離散點策略不僅降低了多點打靶法的收斂難度，同時提升了計算效率。第二級修正策略克服了初始圈次不足的困難，第三級修正通過引入近月點半徑判斷的修正策略保證了滾動時域方法不發(fā)散且減少了修正迭代次數(shù)。最終生成了維持500圈約10年的擬周期NRHO 軌跡，速度消耗在幾十毫米量級。以上設(shè)計方法和設(shè)計結(jié)果可以為長期擬周期NRHO設(shè)計提供重要參考。