起伏地表QR徑向基函數有限差分及其在彈性波逆時偏移中的應用

段沛然, 谷丙洛, 李振春, 李青陽

1 中國石油大學(華東)地球科學與技術學院, 青島 266580

2 深層油氣重點實驗室, 青島 266580

3 中國石油長慶油田分公司勘探開發研究院, 西安 710018

0 引言

目前,油氣地震勘探的重點已由老油田、老區塊的簡單構造逐漸向山地、丘陵等復雜地表區域轉移(劉紅偉等,2011;岳玉波等,2012).這些區域勘探面臨地表起伏大、近地表橫向速度變化劇烈等難題,給地震資料偏移成像帶來巨大的挑戰(裴正林,2004;黃建平等,2014;楊宏偉等,2022).對于復雜起伏地表地震資料的偏移成像方法主要有兩類：一是在偏移前采用高程基準面靜校正,將地震資料校正到浮動或者固定基準面上,然后再實施偏移成像(Berryhill,1979;Yilmaz and Lucas,1986;李振春等,2007);二是基于起伏地表直接進行偏移成像(Wiggins,1984;Beasley and Lynn,1992;Margrave and Yao,2000;何英等,2002;Shragge and Sava,2005;程玖兵等,2006;Liu et al.,2011).當基巖出露,地表高程變化大,近地表橫向速度變化劇烈時,靜校正往往會扭曲波場,降低地震成像的質量.從起伏地表直接進行偏移成像的方法,其算法設計隱含靜校正過程,具有自然適應復雜地表條件的能力,一直是是業內研究的熱點和目標.

由起伏地表直接偏移的成像方法包括射線類偏移、單程波方程偏移和雙程波方程偏移.與射線類(Beylkin,1985;Gray and Bleistein,2009)和單程波方程(Claerbout,1971;Mulder and Plessix,2004)偏移方法相比,基于雙程波方程的逆時偏移不受傾角和偏移孔徑限制,避免了上下行波分離,可對多種波場(一次反射波、多次波、棱柱波等)準確成像,因此在復雜地下構造成像方面具有巨大的理論優勢(Whitmore,1983;Baysal et al.,1983;Gu et al.,2015).波場延拓作為逆時偏移算法的核心環節,其關鍵在于高精度的地震波數值模擬方法.目前,起伏地表地震波數值模擬方法研究主要分為網格劃分和自由地表邊界條件兩個部分.其中,網格劃分可分為規則網格、曲變網格、非結構網格以及無網格.基于規則網格的有限差分方法(Finite Difference Method,FDM)(Kelly et al.,1976;Marfurt,1984;Virieux,1986)具有計算效率高、易于實現、適用于任意復雜介質等優點,是目前應用最為廣泛的地震波數值模擬方法(Ren et al.,2017;吳國忱等,2018; 吳建魯和吳國忱,2018; 段沛然等,2020).為了解決FDM中的起伏地表問題,Jih等(1988)利用具有不同角度的線段擬合地表起伏,采用單邊近似法處理不規則自由表面條件實現起伏地表地震波數值模擬.該方法需采用精細網格剖分實現線段貼合起伏地表,因此計算效率較低.Hayashi等(2001)在FDM中引入局部變網格剖分模擬起伏地表自由表面的瑞雷波.變網格由于依賴于網格形變程度,僅能減少雜散衍射,無法完全消除矩形網格階梯近似所引起的衍射(孫成禹等,2008; 李振春等,2014).Tessmer等(1992)將變網格思想引入交錯網格FDM中,但其僅有二階精度(Hestholm and Ruud,2002),難以應用于實際.Zhang和Chen(2006)根據實際地表起伏劃分曲線網格,實現起伏地表貼體網格FDM.de la Puente等(2014)采用基于完全交錯網格的垂向變換網格和模擬地震波建模的網格變形策略,實現了起伏地表條件下的彈性波數值模擬.Shragge 和Tapley(2017)采用廣義結構網格法求解張量聲波方程.Chen 等(2022)將浸入邊界法與平面波透射邊界相結合,提出一種適用于起伏地表的浸入吸收邊界,該方法基于常規的矩形網格剖分,簡單高效.貼體網格是一類曲變網格,適用于同位網格和交錯網格,使用范圍廣且較易生成.但是貼體網格要求地形起伏的函數處處可導,因此不適用于地表起伏劇烈的區域(如崎嶇地表、近垂直斷崖等地質條件).非結構網格地震波數值模擬的實現方法主要有限元法(K?ser and Iske,2005;董興鵬和楊頂輝,2017)、邊界元法(符力耘和牟永光,1994; 何彥鋒等,2013)、譜元法(Komatitsch et al.,2000;Cristini and Komatitsch,2012)、間斷伽遼金法(Cockburn et al.,2000;K?ser and Dumbser,2006)、格子法(徐義和張劍鋒,2008;孫輝等,2019)等.這些方法均基于非結構網格或非規則網格算子的全空間離散,能夠很好的貼合起伏地表,但是這些方法大多采用全局積分方程弱形式,計算量大,長時間模擬存在不穩定問題.

無網格法是近些年來興起的一類數值計算新方法,它是有限元等傳統方法的重要補充和發展.基于無網格的徑向基函數有限差分方法(Radius-Basis-Function Finite Difference Method,RBF-FDM)能夠有效避免虛假反射,具有節點剖分隨模型速度變化,復雜地質體剖分靈活等優點(劉立彬等,2020).RBF是RBF-FDM中的一類徑向對稱函數,用于計算差分權重,并求解不同類型的偏微分方程(Tolstykh and Shirobokov,2003; Fornberg et al.,2013; Fornberg and Flyer,2015;Dehghan and Mohammadi,2019).在地震領域,Martin 等(2013, 2015)首次將RBF-FDM應用于聲波方程,實現了二維非均勻介質的數值模擬.Takekawa等(2014a,b)研究了RBF-FDM中的自由表面條件,并將哈密頓粒子法引入RBF-FDM中,進行了起伏地表聲波數值模擬.Takekawa和Mikada(2018)在RBF-FDM中提出了一種適用于無網格的自由表面邊界條件,并將其應用于頻域彈性波數值模擬.Li等(2017)進一步將含時-空域優化算子的RBF-FDM應用于聲波數值模擬,同時采用混合吸收邊界條件壓制邊界反射.Takekawa等(2016,2018)通過增加相鄰節點數目來提高數值模擬精度,將多參數泰勒展開應用于非均勻介質RBF-FDM.Liu等(2019)利用RBF-FDM進行頻率域聲波方程數值模擬,采用完全匹配層(Perfectly Matched Layers,PML)邊界條件來壓制邊界反射.Duan等(2021)提出了一種基于頻散關系和穩定性條件約束節點間隔的自適應節點剖分方法,實現了靈活穩定的RBF-FDM聲波數值模擬.Wu等(2021,2022)實現了基于RBF-FDM的聲波逆時偏移和全波形反演.

除了起伏地表地震波數值模擬外,國內外已有多位學者對起伏地表標量波場逆時偏移成像方法進行了研究(張曉波等,2022;孫志廣等,2023;姚宗惠等,2023).徐義(2008)提出了一種適用于起伏地表的格子法疊前逆時度偏移方法.Zhang 等(2010)提出了一種基于地表起伏非反射遞歸算法的疊后逆時偏移算法.劉紅偉等(2011)給出了一種實現起伏地表疊前逆時偏移的方法,該方法通過簡化自由邊界條件,結合GPU加速算法實現了高效穩定的起伏地表疊前逆時偏移.Lan等(2014)基于貼體網格地形“平化”策略較好地擬合平滑地表起伏,實現了貼體網格的起伏地表逆時偏移.Liu等(2017)提出了一種適用于起伏地表的非結構網格法疊前逆時偏移.然而,實際地震波是包含縱橫波的矢量場,將縱橫波的耦合特性綜合應用于基于矢量波場的彈性波逆時偏移,彌補了標量波成像在巖性識別和構造解釋等方面存在多解性的缺陷.曲英銘等(2015)提出一種基于曲坐標系的分層坐標變換法,實現起伏地表條件下的彈性波疊前逆時偏移.Qu等(2021)將此方法推廣到具有起伏地表的棱柱波彈性波逆時偏移方法中.Naveed和Chen(2019)利用曲網格進行波場延拓,利用貼體網格處理起伏地表實現了彈性波逆時偏移.Zhong等(2021)基于Zhang和McMechan(2010)提出的波場分離方法,利用地形起伏相關的濾波器實現了起伏地表彈性波逆時偏移.上述起伏地表彈性波逆時偏移方法均以結構網格剖分為基礎,計算量較大.面對當前復雜的勘探目標,進一步研究起伏地表彈性波逆時偏移方法仍具有重要意義.

綜上所述,基于RBF-FDM的地震波數值模擬方法研究主要局限于水平地表聲學介質,而針對起伏地表彈性介質的RBF-FDM數值模擬的理論和方法研究尚不完善.另外,針對起伏地表彈性波逆時偏移,目前主要采用曲坐標系下的貼體網格等方法進行波場延拓,盡管曲網格能較好的貼合地表起伏,但對于起伏地表的自由邊界條件適用性不足.本文在聲波RBF-FDM數值模擬基礎上,提出一種優化的起伏地表無網格彈性波RTM方法.通過定量分析基于RBF-FDM的彈性波數值模擬的頻散關系與穩定性條件,本文發展了高精度的QR徑向基函數有限差分方法(QR-RBF-FDM),同時提出一種優化的起伏地表自適應節點剖分技術,形成了新的基于無網格的起伏地表彈性波數值模擬方法.由于起伏地表無網格邊界條件加載困難,本文提出了適用于無網格的精確自由邊界條件和彈性波混合吸收邊界條件.此外,本文將此無網格RBF-FD應用于精確的縱橫波場矢量分解公式(Gu et al.,2019),實現了起伏地表彈性波逆時偏移成像.通過對高斯山丘模型,起伏凹陷模型和起伏地表Marmousi-2模型的數值試算驗證了本文提出方法在起伏地表彈性波數值模擬與逆時偏移成像中的可行性與有效性.

1 徑向基函數有限差分方法彈性波數值模擬

1.1 徑向基函數彈性波有限差分方法

各向同性介質中,彈性波二階位移方程可表示為

(1)

其中,u(x,z,t)和w(x,z,t)表示在空間x、z方向上的位移波場分量,ρ(x,z)表示介質密度,λ(x,z)和μ(x,z)為拉梅常數.在起伏地表條件下,傳統的FDM很難滿足要求.基于無網格節點離散模型的RBF-FDM能夠有效避免虛假反射,具有剖分節點隨模型參數變化,起伏界面處理靈活等優勢(劉立彬等,2020).本文將RBF-FDM引入彈性波波動方程數值模擬中,以便獲得高精度的彈性波地震波場.

RBF-FDM是基于一組局部無序的離散節點,根據與節點距離相關的徑向基函數構造差分算子矩陣實現偏微分方程.在任一時刻,若給定Ω區域內存在波場U(x)及無序離散節點x={x1,x2,…,xn},節點位置及參數由點生成方法可知,波場U(x)可由徑向基函數φ(r)近似表示為

(2)

式中,r節點間距(中心點與其最近鄰近節點的距離),rj=‖x-xj‖表示鄰近節點xj距離中心節點x的距離,‖·‖表示歐幾里得范數;N為中心節點x差分模板所需的鄰近節點個數,根據鄰近當前任意點的距離選取差分模板的范圍,選擇N個最近點,記為差分模板,差分模板中的點按距離遠近排序;{c1,c2,…,cN}為待定的RBF-FD系數.根據無網格RBF-FD基本原理,對于任意線性偏微分算子L,中心點節點x0處波場U(x)|x=x0的任意空間偏導數可以表示為

(3)

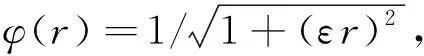
(4)

其中,徑向基函數系數矩陣的條件數是影響RBF-FD差分系數求解的重要因素,為保證差分方程的穩定,條件數的取值范圍應在106～108(Flyer et al.,2014;Martin et al.,2015;Li et al.,2017).實際中,該條件數由當前差分模板的節點分布,差分格式,節點間隔和徑向基函數類型及形變參數等相關.根據條件數經驗取值范圍(106～108),在類均勻分布(如圖1)的模型中得到了一組節點數與節點間隔和形變參數的最佳取值范圍(見表2,參見Li et al., 2017).

表1 徑向基函數有限差分方法中常用的徑向基函數Table 1 Commonly used radial basis function in RBF-FDM

采用RBF-FDM求解彈性波方程,首先通過時間二階差分來代替式(1)中的時間微分算子如下：

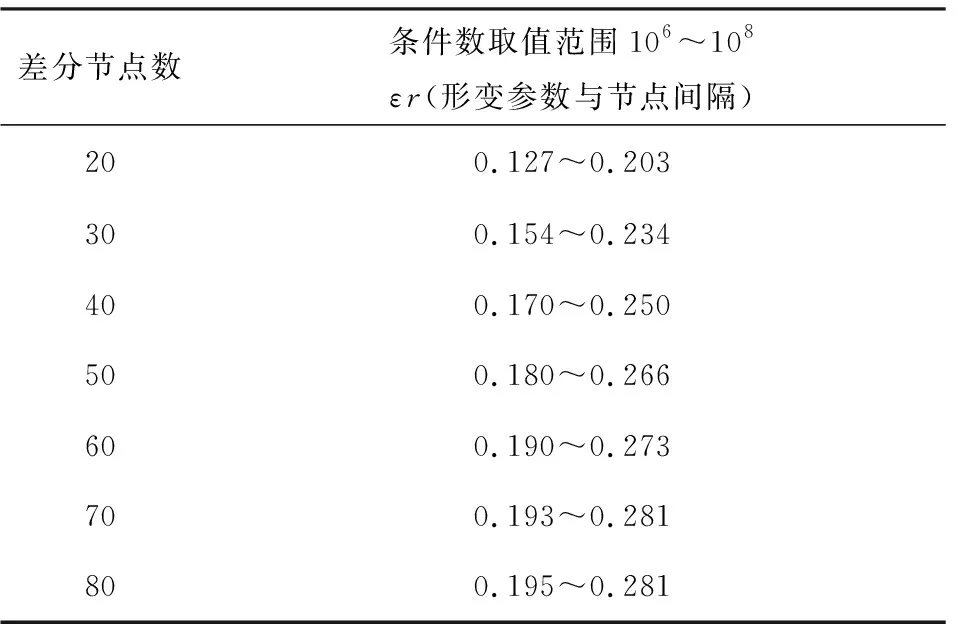
表2 類均勻分布情況下RBF-FD最優差分節點數、節點間隔和形變參數的選取Table 2 Optimal ranges of parameters for RBF-FD with different numbers of neighbors in quasi-uniform distribution

(5)

其中,上標l為當前時刻,τ為時間步長.采用RBF-FDM差分算子對式(1)中u分量的空間導數進行離散：

(6)

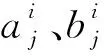
(7)

本文采用RBF-FD中常用的K-D算法(KNN-Search)尋點,能夠不占用計算量找到計算域中任一中心節點差分模板中的N個鄰近差分節點.

1.2 數值頻散分析與穩定性條件

在平面波條件下假設下,彈性波場可以表示為

(8)

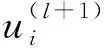
(9)

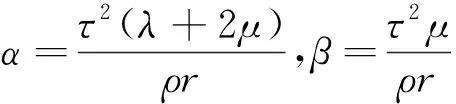
(10)

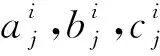
(11)

對式(11)中兩式相乘得：

+β2(A+B)]=0,

(12)

根據式(12)可得：

(13)

(14)

將式(10)中A,B代入式(11)化簡可得RBF-FD頻散關系為

(15)

其中：

(16)

其中,θ表示相角.

穩定性條件也是衡量微分方程數值求解算法有效性的重要指標.本文根據傅里葉譜分析法(Von Neumann,1950)推導RBF-FD情況下的穩定性條件.此處,將式(1)表示為矩陣形式：

(17)

為了方便起見,進一步將式(17)簡寫為

(18)

式中U(t)=[u(t),w(t)]T為多分量波場矢量,Q為二階矩陣.

應用RBF-FD的思想求解彈性波方程,對式(18)中的時間導數進行二階有限差分離散可得：

+O(Δt2M),

(19)

將式(18)代入式(19)得：

(20)

設G(kx,kz)是Q(kx,kz)的傅里葉變換對,對式(20)進行空間傅里葉變換可得：

U(t+Δt,kx,kz)-2U(t,kx,kz)+U(t-Δt,kx,kz)

(21)

將U(t,kx,kz)的系數矩陣記為

(22)

則式(7)改寫為

Un+1=2Un-Un-1+AUn,

(23)

式中n表示當前時刻,根據傅里葉分析方法,令：

(24)

聯立式(23)、(24)得：

(25)

式中,E為單位矩陣,B為增長矩陣.

根據Von Neumann穩定性條件可知,當增長矩陣特征值的絕對值小于或等于1時,遞歸是穩定的,即時間穩定性條件是增長矩陣B的譜半徑不大于1.由式(25)可知,B的特征值β應滿足：

|βE-B|=|β2E-βA-2E|=0,

(26)

由式(26)可知,β的取值與矩陣A有關,因此先求取的A特征值γ：

(27)

根據式(22),若G的特征值為η,求取A特征值γ需要首先求取G的特征值η.根據矩陣Q的表達形式,η應滿足：

(28)

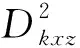
(29)

根據行列式規則式(28)可化簡為

+Dkzz)2=0,

(30)

利用2次多項式的求解方法計算得到η的2個特征值為

(31)

由式(27)可知,矩陣A特征值γ為

(32)

由于A為2階方陣,且有2個互異的特征值,因此矩陣A可對角化,有：

A=PΛP-1,

(33)

式中P為可逆矩陣,Λ為A的特征值構成的對角陣,具體表示為

Λ=diag{γ1,γ2},

(34)

由式(27)可得：

|β2E-βΛ-2E|=0,

(35)

由式(35)可得B的特征值β和A的特征值γ的關系式為

β2-βγ-2=0,

(36)

即：

(37)

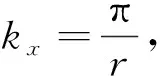
(38)

若系數矩陣A的特征值γ的絕對值小于或等于1,則滿足穩定性條件.對比|γ1|和|γ2|表達式可知,RBF-FD差分格式需滿足的穩定性條件是：

(39)

2 QR徑向基函數有限差分方法

在常規RBF-FDM中,形變參數ε趨近于0時,徑向基函數趨于平坦而擬合精度越高.然而平坦的徑向基函數會導致差分矩陣的病態,影響波場延拓的穩定性.Flyer等(2012)研究了含泰勒多項式的RBF-FDM,提高了數值模擬的穩定性,但該方法依賴模型參數的取值,在處理復雜構造模型時,構造泰勒多項式所增加的參數將會導致差分矩陣的病態,使得波場傳播不穩定.為了提高模擬精度且不落入病態問題,Fornberg等(2013)提出一種無需形變參數的高斯QR基函數,將其成功用于插值問題.本文將高斯QR基函數的思想引入RBF-FD中,在笛卡爾坐標系下構造差分矩陣,將高斯徑向基函數轉換至極坐標系,并展開為切比雪夫多項式的形式,利用QR分解法求解由切比雪夫多項式構成的差分矩陣,有效解決了徑向基函數的形變參數取值和矩陣病態問題,在保證精度的同時增強波場傳播的穩定性.

QR徑向基函數法利用切比雪夫多項式T(x)對高斯徑向基函數φ(r)=e-i(εr)2級數展開(Fornberg et al., 2011),并將其變換至極坐標系(r,θ)得到：

(40)

其中切比雪夫多項式表示為

(41)

其中,j≥0,0≤m≤(j-p)/2;當p=0時,j為偶數,當p=1時,j為奇數;公式(40)中尺度因子dj,m為

(42)

當形變參數ε適當取值時,尺度因子dj,m的取值范圍為[0,1];公式(40)中參數cj,m和sj,m為

(43)

其中參數b0=1,bm=2,m>0;參數t0=1/2,tj=1,j>0;F2為超越方程組,其中參數αj,m=(j-2m+p+1)/2,βj,m=[j-2m+1,(j-2m+p+1)/2];由此,公式(40)可改寫為矩陣形式：

(44)

其中,矩陣C由參數cj,m和sj,m構成,三角陣D由尺度因子dj,m構成.

利用QR分解對矩陣C進行分解代入公式(44)得：

φ(x)=Q·R·D·T(x),

(45)

將公式(45)代入公式(40)得：

(46)

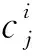
(47)

求解公式(47)可得到優化的差分系數.由于切比雪夫多項式的定義域為r∈[-1,1],計算差分系數時需將當前點的差分模板預先縮放到[-1,1]的范圍內.

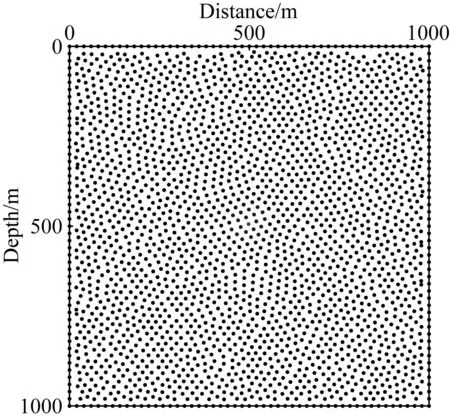
圖1 類均勻節點剖分示意圖

這里采用一個均勻介質模型研究QR徑向基函數有限差分方法(QR-RBF-FDM)的擬合精度、穩定性及其頻譜分析.介質縱波速度為3000 m·s-1, 橫波速度為1732 m·s-1,模型大小為1000 m×1000 m,節點間隔為10 m,時間步長為0.5 ms,最大記錄時間為1.0 s.采用20 Hz雷克子波作為縱波震源,位于近(500 m, 20 m)處.圖1給出了類均勻節點分布圖,紅點和藍點分別表示任意中心差分點及其對應的無網格差分模板包含的N個差分節點.圖2給出不同方法得到的點(500 m, 0 m)處的波形圖及誤差曲線圖.其中,解析解(analytical_solution)由Cagniard-De Hoop法(De Hoop, 1960)得到,FDM表示時間2階空間10階精度的有限差分.由圖2a單道記錄與圖2b振幅誤差曲線圖可見：QR-RBF-FDM 和 FDM的波形和振幅與解析解基本吻合,而RBF-FDM的模擬結果取決于形變參數取值.當形變參數為0.01時,RBF-FDM的波形和振幅與解析解基本吻合,而當形變參數為0.1或0.001時,RBF-FDM的模擬結果與解析解偏差很大.圖2c為單道記錄對應的頻譜圖,QR-RBF-FDM能夠有效抑制形變參數導致的差分矩陣病態問題,獲得與FDM和解析解相近的頻譜;常規的RBF-FDM采用不適合的形變參數將引起波形震蕩,時間空間頻散分別出現在波前的淺部和尾部,同時引起了頻譜畸變,對頻譜影響較大.由此可知,QR-RBF-FDM比常規的RBF-FDM具有更高的模擬精度,且形變參數的取值不影響QR-RBF-FDM的結果.圖3為QR-RBF-FDM、常規RBF-FDM與FDM的計算效率對比.與FDM相比,QR-RBF-FDM與RBF-FDM的計算成本主要來源于差分系數計算和差分方程迭代兩個方面.其中,差分方程迭代過程與FDM基本一致,而盡管二者僅需在整個計算過程中計算一次差分系數,但由于每個節點進行差分系數矩陣求解仍然需要消耗巨大的計算成本,因此QR-RBF-FDM與RBF-FDM在計算成本和計算時間方面為FDM的4倍左右(如圖3).QR-RBF-FDM求解差分系數過程計算相對常規的RBF-FDM更加復雜,因此計算時間較長,但考慮到無需選擇形變參數,因此可避免因形變參數選擇不當而產生的計算冗余.

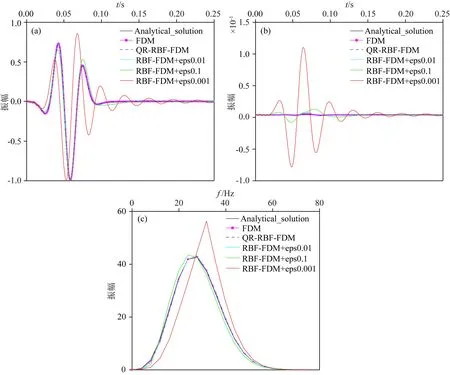
圖2 均勻模型(500 m, 0 m)處不同方法(a) 單道記錄波形; (b) 振幅誤差曲線; (c) 對應的頻譜.

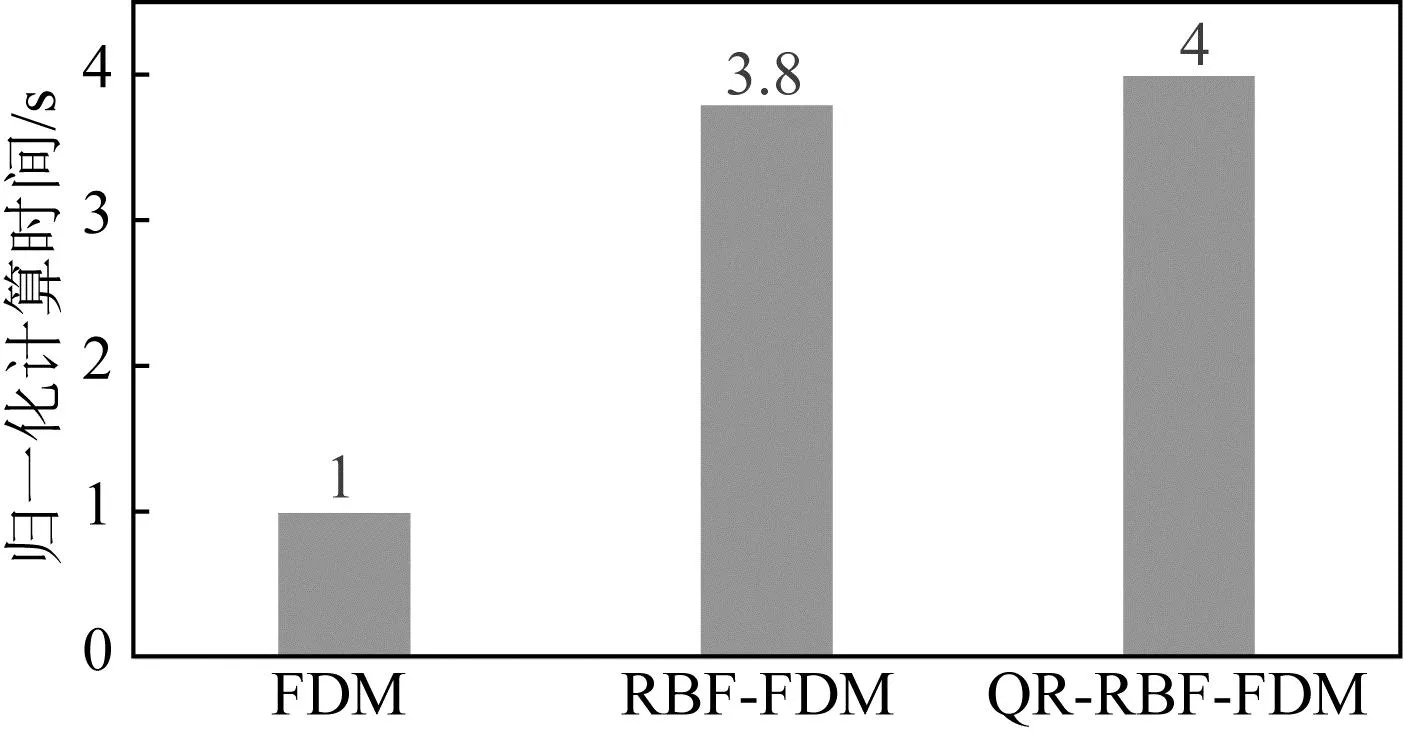
圖3 均勻模型不同方法歸一化計算時間對比圖

3 起伏地表自適應節點剖分方法

節點剖分是RBF-FDM的第一步,也是連接速度模型與數值模擬算法的關鍵.Duan等(2021)提出的自適應節點剖分法利用頻散關系和穩定性條件約束節點間隔的取值范圍,能夠在矩形計算域內生成適應模型速度的非均勻節點分布.但考慮起伏地表的不規則邊界與地下介質的不均勻性,Duan等(2021)的方法將不再適用.因此,在Duan等(2021)的基礎上,本文提出一種自適應起伏地表節點剖分法,邊界節點貼體起伏地表,并在內部節點剖分過程中,對起伏地表和地下構造變換劇烈的區域依據速度變化的梯度大小進行自適應調節.起伏地表節點剖分方法(見圖4)采用如下的步驟：

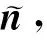
(2)利用自適應節點剖分法進行內部節點剖分,剖分方式如圖4bi—iii所示.(i) 設定最下層邊界節點為潛在點位.(ii) 根據速度模型參數確定各起始點位的節點間距,設置以起始點位為中心,半徑為節點間距的圓域.(iii) 刪除此圓域內所有其他的潛在點位,在刪除節點的圓周范圍內放置等距的新點位.由下層潛在點位迭代直至與邊界節點距離小于節點間距的一半d/2.記錄內部節點的初始坐標(ξ,η)對應的速度模型參數,如圖4b(iv)所示.

(3)刪除與邊界節點間距小于d/2的內部節點,如圖4c所示.

(4)根據自適應節點控制方程(式(51)),將內部節點由初始坐標調整到新的坐標(x,z),通常,需要四次以上的迭代獲得滿足精度要求的節點分布,得到每個節點的坐標及對應的速度模型參數,如圖4d所示.

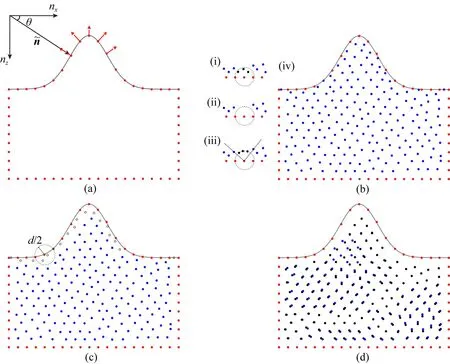
圖4 起伏地表自適應節點剖分過程示意圖

為了計算起伏地表上節點的法線方向,步驟1中地表節點的坐標變換到極坐標系：

(48)

式中(x,z)表示笛卡爾坐標系中地表節點的位置向量,(r,θ)表示極坐標系下地表節點的位置向量,取速度模型左上頂點作為極點,則關于極角θ的梯度為

(49)

由此可知,法向量的分量nx和nz可表示為

(50)

其中sgn(·) 表示常用符號函數,g表示梯度.在步驟4中,引入自適應網格理論(Saltzman and Brackbill, 1982)中的控制方程對自適應節點剖分法生成的無網格節點位置進一步調整,控制方程為

(51)

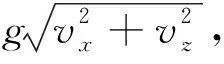
(52)

J=xξzη-xηzξ,

(53)

其中J表示雅可比多項式,其中一階導數?x/?ξ,?x/?η,?z/?ξ和?z/?η簡寫為xξ,xη,zξ和zη.

無網格與基于坐標變換法的貼體網格和曲網格各有優劣.(1)貼體網格和曲網格是起伏地表條件下的地震波模擬中的重要方法,其網格易于生成且在曲坐標系下可直接使用水平地表假設的自由邊界條件.與這兩種網格相比,無網格的優勢在于無需坐標變換,直接采用彈性波、聲波等方程直接進行差分,后期研究中更適用于復雜的黏性介質或各向異性方程.(2)貼體網格和曲網格在生成過程中,僅能通過一些密度函數進行疏密調節,筆者認為此種調節疏密通常是不可控的,因為網格數不變的情況下調節一個部分疏密必將使得另一部分密疏,一定程度上將導致數值頻散以及穩定性問題.與這兩種方法相比,無網格以模型速度、密度等參數為依據,直接生成滿足模型剖分條件的節點分布,不存在調節后一部分點過密一部分點稀疏的現象,因此相對更加具有數值穩定性.(3)貼體網格和曲網格本質上仍然是固定的網格間隔,這就造成在深層、中深層進行數值模擬,網格過密造成冗余.通過文獻調研可知,貼體網格往往需要與變網格相互結合以提高其計算效率.與之相比,無網格節點在剖分過程中根據速度、密度等參數可自適應調節節點間距,因此在深層、中深層等復雜構造中可由細網格自然過渡到粗網格.

4 與地形相關的邊界條件

4.1 無網格自由邊界條件

RBF-FDM的優勢在于處理起伏自由邊界.在自由表面是固體地球與空氣層之間的物性突變面,常規自由邊界條件通常假設垂直自由表面的應力為0(Lan and Zhang, 2011),二維水平自由表面(z=0)處的表達式為

(54)

地形起伏會明顯影響地震波場的傳播,此時水平自由邊界條件的假設將不適用.為了在RBF-FDM中精確處理起伏地表,需要將無網格節點自然放置在起伏的曲面地形上,利用起伏地表自適應節點剖分方法獲得起伏界面的法線分量,在此基礎上重新推導起伏界面的精確自由邊界條件.圖5顯示了規則網格和無網格的剖分示意圖.

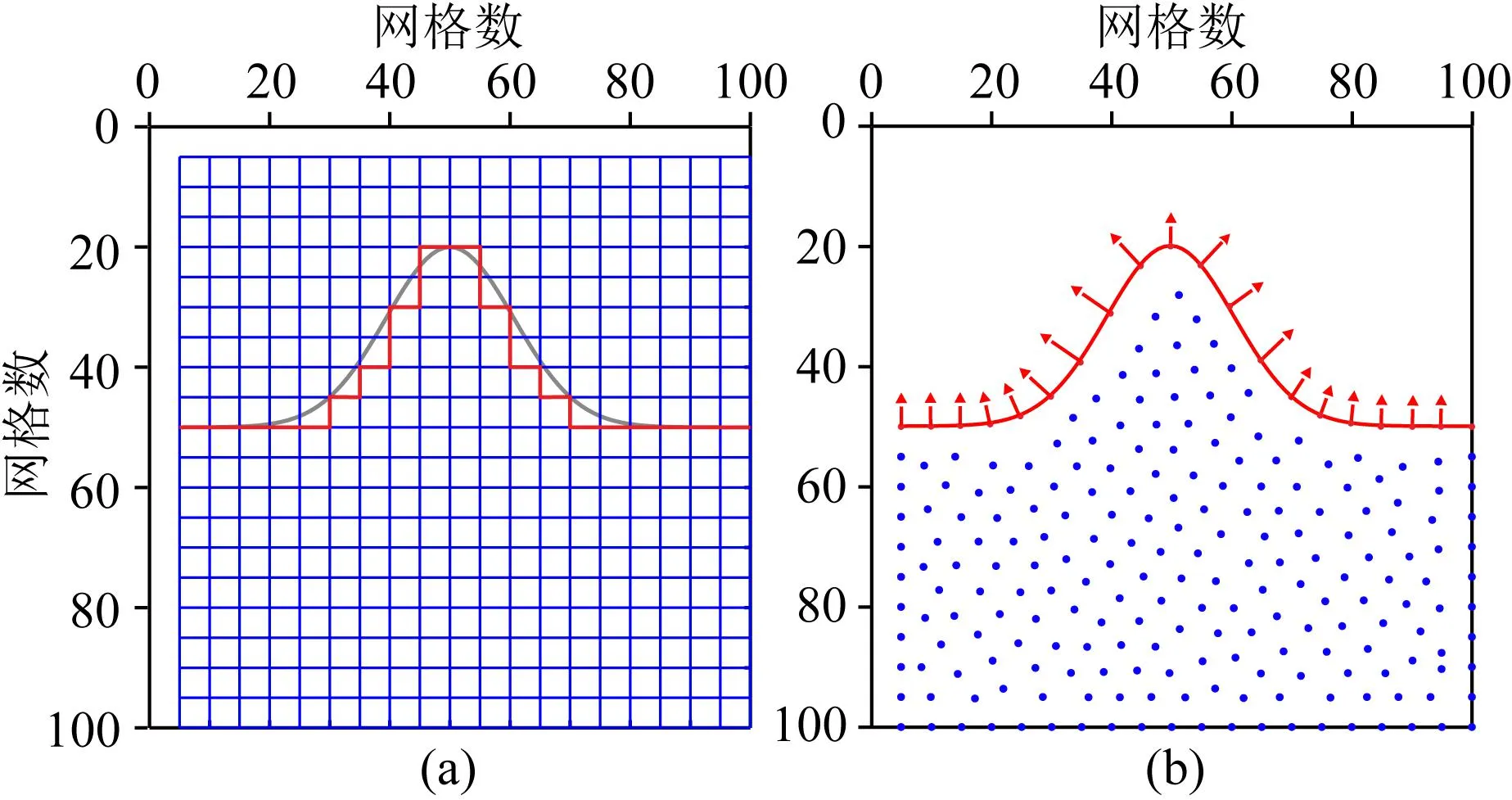
圖5 網格剖分示意圖(a) 規則網格; (b) 無網格節點.紅色曲線表示起伏地表, 藍色節點表示內部節點,紅色節點表示地表節點,箭頭表示地表節點的法向量方向.

因此,本文采用Dirichlet邊界條件推導出無網格節點的自由曲面邊界條件,將其應用于貼合實際地形的RBF-FDM具有更高的精度.Dirichlet邊界條件如下：

(55)

其中σxx和σzz為正應力,σxz為切應力.在此基礎上,通過自適應節點生成方法求出了與起伏地表垂直的外法向x分量nx和z分量nz.因此,應力分量可以表示為

(56)

將式(56)代入式(55),經過化簡可以得到起伏地表自由邊界條件：

(57)

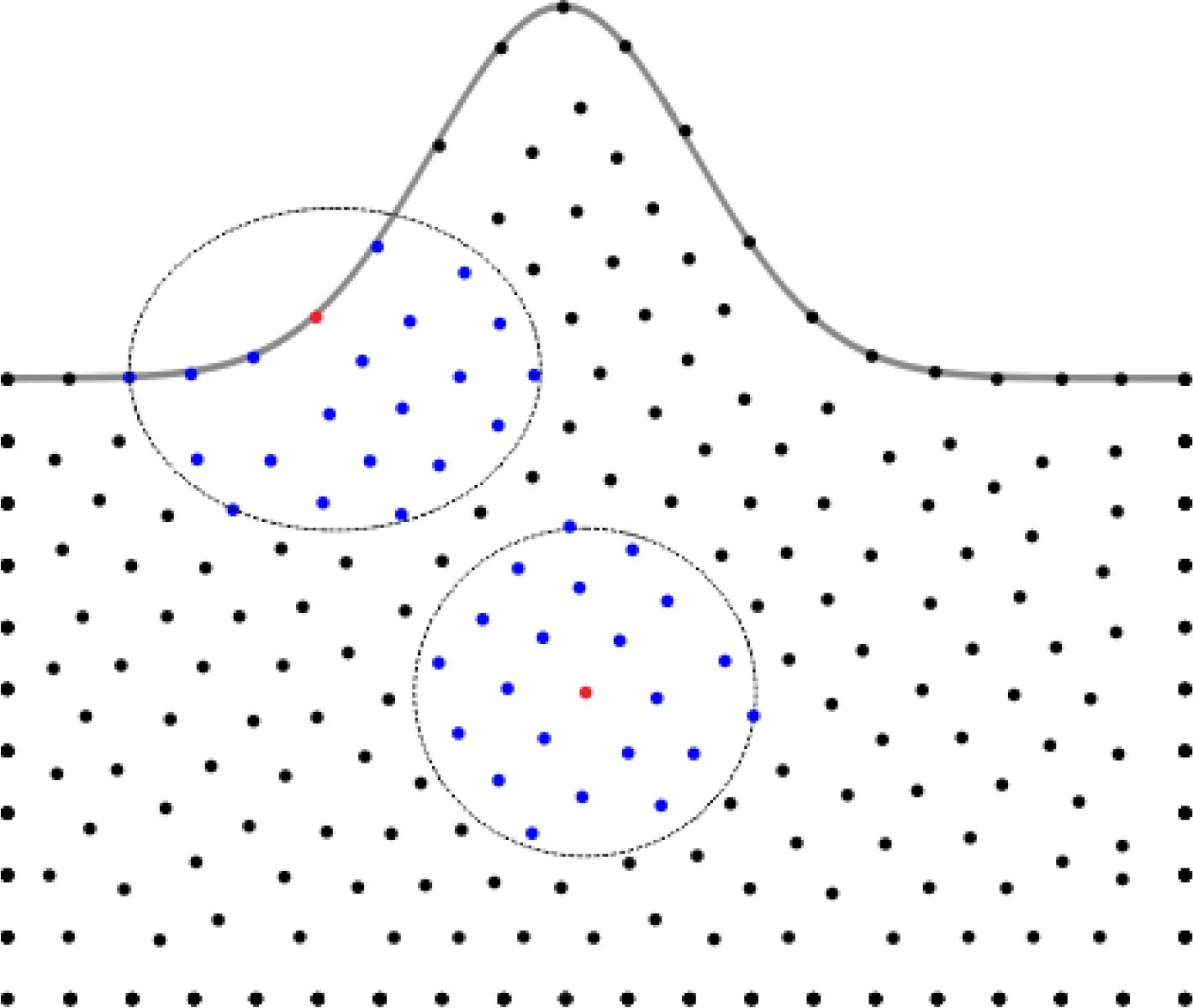
圖6 差分模板示意圖紅點為中心點,藍點為中心點對應的差分點,橢圓區域為邊界節點差分模板,圓形區域為內部節點差分模板.

其中,地表界面上的法向量的分量nx和nz可式(56)計算得到.在規則網格FDM中,通常需在自由表面上方引入虛擬點以滿足自由表面處邊界條件的差分格式.與之相比,在RBF-FDM中,計算節點可以放在任意位置進行差分,邊界節點完全貼體起伏地表分布.因此無需特殊處理,在邊界節點處采用如圖6橢圓區域所示差分模板,利用QR-RBF-FDM獲得邊界節點處的空間導數并運用于式(57)實現無網格的自由邊界條件.其中一階空間導數可由RBF-FDM近似得到：

(58)

其中x0為地表節點的坐標,mj和nj表示由QR-RBF-FDM計算得到的一階差分系數,同理可得垂直分量w的一階空間導數的表示形式.本文由Dirichlet邊界條件出發,推導了基于RBF-FD的自由邊界條件,相對于與應力鏡像法等常規方法而言,該方法無需設置虛擬層,在笛卡爾坐標系下直接求解邊界條件,處理方式簡單且計算精度高.本文在數值算例中將對此進行驗證.

4.2 無網格彈性波混合吸收邊界條件

利用RBF-FDM進行起伏地表彈性波逆時偏移時,必須考慮起伏地表情況下的邊界吸收問題.基于Li 等(2017)提出的分段光滑曲線邊界節點生成方法,本文在現有邊界節點基礎上,基于彈性波Clayton和Engquist(CE)單程波方程推導了無網格起伏地表條件下的混合吸收邊界條件.起伏地表條件下的彈性波CE單程波方程表示為(任志明,2016)：

(59)

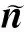
(60)

將式(59)寫為位移分量方程的形式可得：

(61)

通過引入邊界區域每個節點對應的最近內點,為單程波方程提供穩定的差分：

(62)

其中,位移分量u和w的上標-1,0,1表示前一時刻,當前時刻與后一時刻,邊界區域的節點(表示為下標B)與其對應的最近內點(表示為下標I)構成的差分項Al和Bl(l=1,2,3,4)為

(63)

(64)

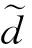
(65)

在此基礎上,在邊界區域的同時采用雙程波方程與上述單程波方程,即可構成起伏地表條件下的無網格混合吸收邊界.混合吸收邊界條件實現步驟(Liu and Sen, 2010)如下：

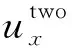
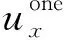
(3)對于邊界區域,將雙程波波場和單程波波場加權平均得到最終的波場：

(66)

其中,加權系數為

aBi=(i-1)/N.

(67)

5 基于徑向基函數有限差分方法的彈性波逆時偏移

在無網格模型參數化的基礎上,我們開展了基于RBF-FDM的彈性波逆時偏移成像方法應用研究.逆時偏移的理論基礎是Claerbout(1971)提出的時間一致性原理,即反射面存在于地層內下行波波至時間與某一上行波波至時間相一致之處.因此QR-RBF-FDM彈性波逆時偏移成像可分為三個部分：一是基于QR-RBF-FDM震源波場的正向延拓,二是基于QR-RBF-FDM檢波點波場的逆向延拓,三是應用成像條件獲得偏移成像結果.波場分離是彈性波RTM至關重要的環節.Gu等(2019)解決了亥姆霍茲分解導致的波場振幅和相位畸變,建立了精確的波場分解和重新組合方程,并實現了3D標量波彈性波逆時偏移,該方法能夠直接獲得具有正確振幅、相位和物理單位的偏移結果.本文基于Gu等(2019)的方法,我們推導得到在無網格模型參數化條件下通過RBF-FDM實現的精確縱橫波波場分離方程,在正向和逆向波場延拓過程中,利用無網格震源波場和檢波點波場進行精確的縱橫波波場分離,并應用互相關成像條件得到成像結果.

根據Gu等(2019)的方法推導,精確的波場分離方程如下：

(68)

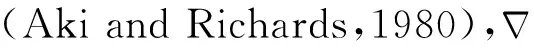
(69)

其中,vp和vs為P-和S-速度.由于無網格法的本質是局部無序的離散節點,無法直接求解式(68)、(69)中的積分.考慮到矢量場V僅有子波項與時間有關,因此在正向和反向波場計算過程中,對震源子波做二次積分提取式(68)、(69)中的積分,矢量場中P和S勢則已包含積分,即可去掉式(68)、(69)中的積分.將式(68)代入式(69)可得：

(70)

根據散度、旋度和梯度的關系求解式(68)得：

(71)

采用QR-RBF-FDM對式(71)進行離散,代入式(6)二階空間算子可得：

(72)

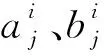
(73)

其中x=(x,y,z)為空間向量;其中sm和rn分別表示源波場的m波模式和接收器波場的n波模式.

6 數值算例

6.1 高斯起伏模型

本節通過兩類高斯起伏地表模型(凸型模型和凹型模型)驗證在自由邊界條件情況下本文方法的有效性,如圖7a、b所示.模型大小為2 km×1.5 km,其中凸型高斯函數為

(74)

凹型高斯函數為

(75)

我們分別對兩類模型采用自適應起伏地表節點剖分法和規則網格剖分法進行離散化.圖8展示了自適應起伏地表節點剖分法離散的結果,由于本測試選用均勻速遞模型以測試起伏自由地表下QR-RBF-FDM的可靠性和穩定性,在速度層上為真空,地表采用自由地表條件,矩形邊界采用無網格彈性波混合吸收條件.模型參數設置如下：縱波速度為3000 m·s-1,橫波速度2000 m·s-1,而對應的自適應起伏地表節點剖分結果呈現出節點間隔相同的特征,其間隔大小為10 m(事實上當速度非均勻條件下,自適應起伏地表節點剖分結果的節點間隔會呈現出不同速遞區域的差異化現象,我們將在后續模型測試中展示).圖9展示了規則網格剖分結果,其正交方向的網格間隔統一為10 m.圖9中紅線部分為高斯起伏界面位置,由于規則網格剖分無法精確捕捉真實的界面位置,因此實際數值模擬過程中,將選取縱向最接近真實界面位置的點作為該模型的自由邊界頂點.

兩類高斯模型測試過程中,時間間隔統一為0.5 ms,采樣點數為2001,總時長為1 s.震源選取主頻為20 Hz的雷克子波,震源位置坐標為 (0.4 km, 0 km).與常規FDM相比(如圖10所示),圖10展示了利用QR-RBF-FDM所得的不同時刻凸型高斯起伏地表模型波場快照,圖8d和圖11中對地震相做了詳細的分析,并在記錄上對波的類型做了相應標注.對比可知,常規FDM和本文方法均能夠較好地處理起伏地表,波場快照中能夠清晰地呈現出直達P波、反射PP波、反射PS波和面波R.但與常規FDM不同,QR-RBF-FDM在起伏構造中沒有產生臺階散射,模擬結果更準確,反射波同相軸更清晰.對比二者數值結果可得以下結論：(1)在0.2 s之前,波在水平地表傳播,QR-RBF-FDM和常規FDM的模擬結果基本一致;(2)0.2 s至0.6 s之間,波經過了起伏地表,常規FDM模擬的波場中產生大量“波紋狀”的次級散射波,這些是由規則網格離散所造成的臺階散射效應.與之不同,QR-RBF-FDM的地表節點分布完全貼合了起伏地形,因此QR-RBF-FDM模擬的波場不存在上述次級散射,展現出了該方法對于復雜區域模擬的優勢;(3)0.6 s之后,波穿過起伏地表并在水平地表繼續傳播,該階段QR-RBF-FDM和常規FDM的模擬結果基本相同,該結論與0.2 s之前的情況一致.圖12和圖13展示了凹型高斯起伏地表模型波場模擬結果,對比該結果可以得出與凸型高斯起伏地表模型類似的結論.進一步地,對比圖11和圖13中波場快照可知,凸起和凹陷模型在傳播過程中均會產生直達波P、反射縱波PP、反射橫波PS和面波R.與凸起模型相比,0.6時地震波圍繞凹陷模型成回轉形式向前擴散,無論直達波或是面波在正方向產生了很強的散射.圖14和圖15分別為兩類模型采用QR-RBF-FDM和FDM模擬得到的地震記錄,從中可以很清晰地看出QR-RBF-FDM相較于FDM在消除階梯散射上的優勢,且面波同相軸清晰.綜上可得,常規FDM和QR-RBF-FDM方法有很大的區別,QR-RBF-FDM得到的波場在起伏界面處非常穩定,并且不會產生大量次級散射,能夠準確地對自由邊界條件下的起伏地表模型進行數值模擬.

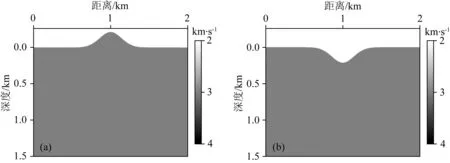
圖7 均勻介質起伏地表模型(a) 凸型高斯模型; (b) 凹型高斯模型.

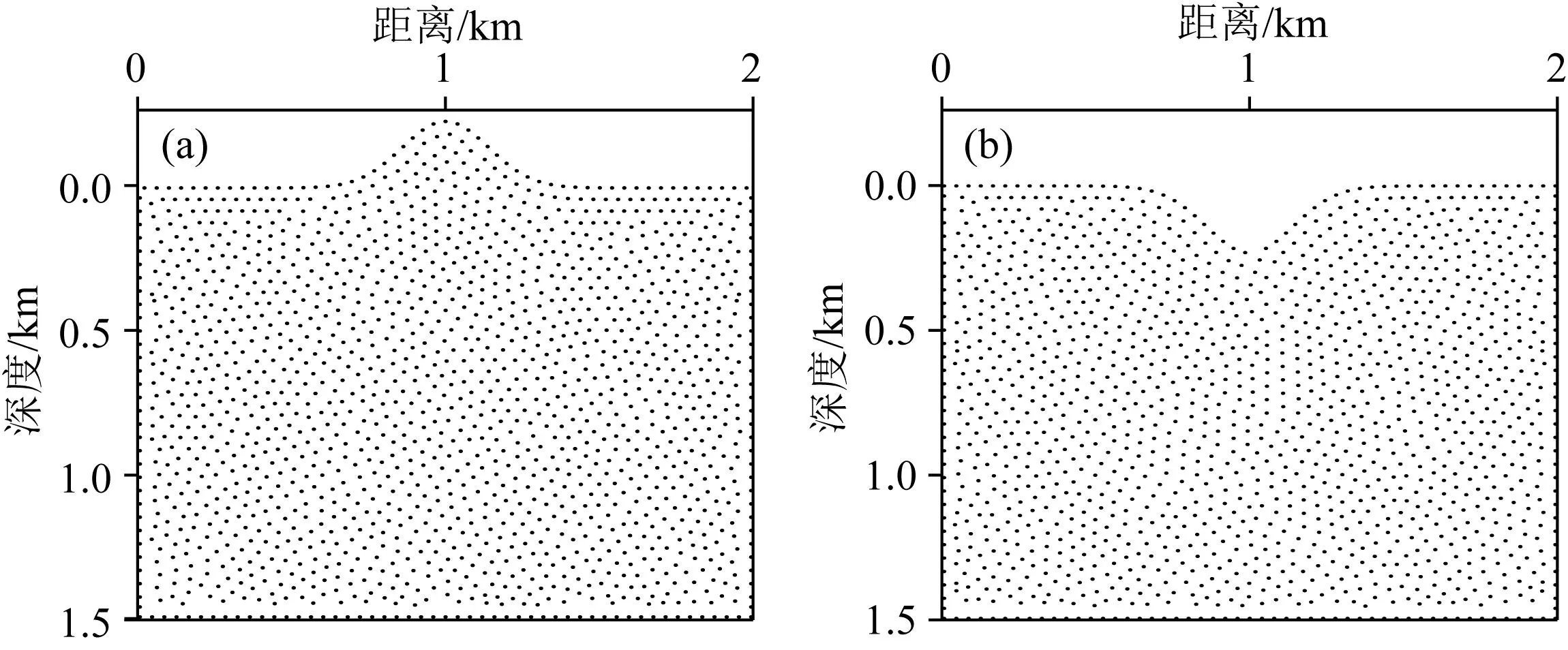
圖8 均勻介質起伏地表模型自適應起伏地表節點剖分結果(a) 凸型高斯模型; (b) 凹型高斯模型.

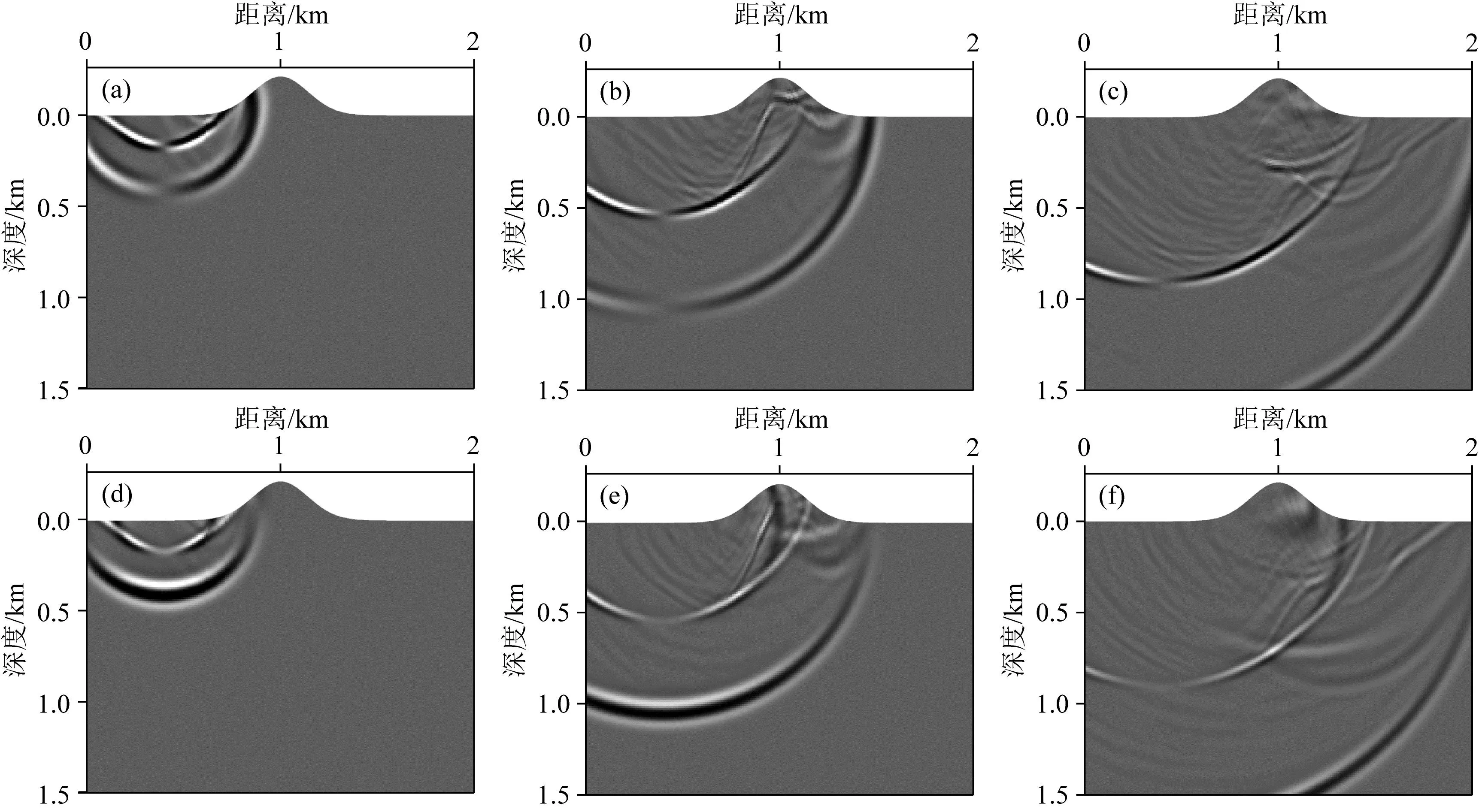
圖10 凸型高斯起伏地表模型常規FDM波場快照(a) 0.2 s水平分量; (b) 0.4 s水平分量; (c) 0.6 s水平分量; (d) 0.2 s垂直分量; (e) 0.4 s垂直分量; (f) 0.6 s垂直分量.

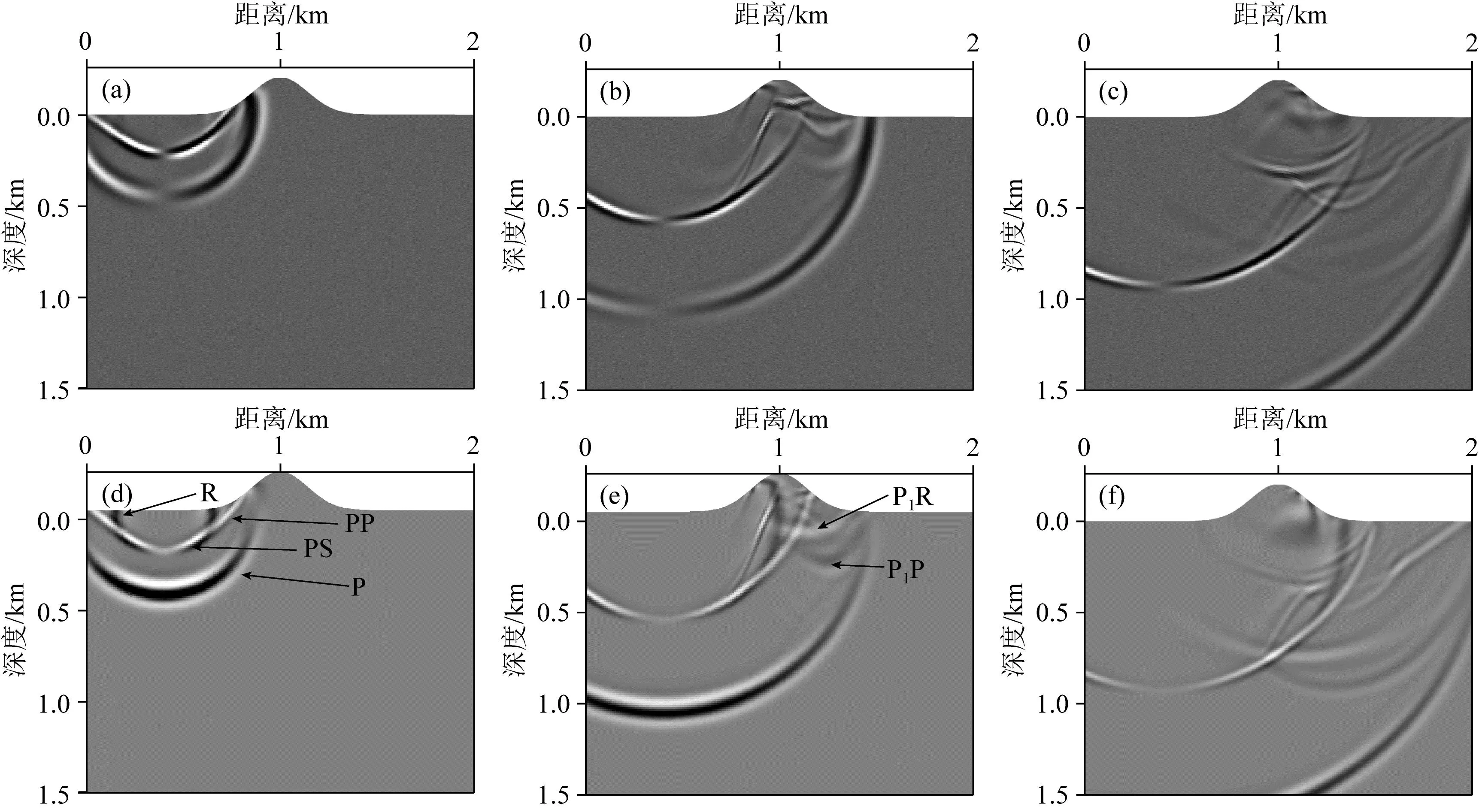
圖11 凸型高斯起伏地表模型QR-RBF-FDM波場快照(a) 0.2 s水平分量; (b) 0.4 s水平分量; (c) 0.6 s水平分量; (d) 0.2 s垂直分量; (e) 0.4 s垂直分量; (f) 0.6 s垂直分量.

6.2 起伏凹陷模型

本節利用起伏凹陷模型驗證非均勻模型下自適應起伏地表節點剖分法和QR-RBF-FDM的穩定性和適應性,此時地表及矩形邊界采用無網格彈性波混合吸收條件.該模型見圖16,模型大小為6 km×4 km,地表起伏函數為6.1節兩類高斯函數的組合.圖17展示了自適應起伏地表節點剖分法離散的結果.與圖17b中常規節點剖分方法采用統一尺度步長相比,圖17a基于自適應起伏地表節點剖分方法中節點間距隨著速度增加而變大,范圍在10 m至15 m之間.基于該模型進行數值模擬,時間步長為0.5 ms,記錄時間長度為3 s,選取主頻為20 Hz的雷克子波作為震源時間函數,檢波點均勻布設于地表,接收范圍為4 km,相鄰檢波點間距為10 m.

圖18給出了不同時刻QR-RBF-FDM模擬的波場快照,震源位于地表橫向3 km處.對比不同時刻波場可知,在近地表區域模擬的波場不存臺階散射,波傳播至深層區域時(即節點間隔增大區域)仍然穩定且無頻散現象.由圖19的不同炮點位置(地表x方向坐標1 km, 3 km 和5 km處)激發的地震記錄可以觀察到,不論在地表任何位置激發的震源,QR-RBF-FDM都能很好地處理起伏地表,采用無網格彈性波混合吸收條件后地震記錄中可以清晰地看出直達波,反射波,轉換波的發育而無面波與散射波,驗證了方法的正確性.綜上可知,本文提出的QR-RBF-FDM不僅通過靈活的自適應起伏地表節點剖分法提供一種穩定的離散節點模型,而且與常規RBF-FDM相比無需選取形變參數,大幅提升了無網格算法的計算效率和計算精度.與常規曲坐標系算法相比,QR-RBF-FDM差分形式更為簡單,更易于推廣.

圖12 凹型高斯起伏地表模型常規FDM波場快照(a) 0.2 s水平分量; (b) 0.4 s水平分量; (c) 0.6 s水平分量; (d) 0.2 s垂直分量; (e) 0.4 s垂直分量; (f) 0.6 s垂直分量.

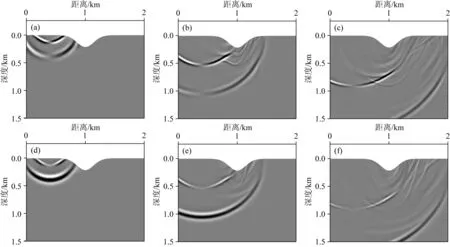
圖13 凹型高斯起伏地表模型QR-RBF-FDM波場快照(a) 0.2 s水平分量; (b) 0.4 s水平分量; (c) 0.6 s水平分量; (d) 0.2 s垂直分量; (e) 0.4 s垂直分量; (f) 0.6 s垂直分量.

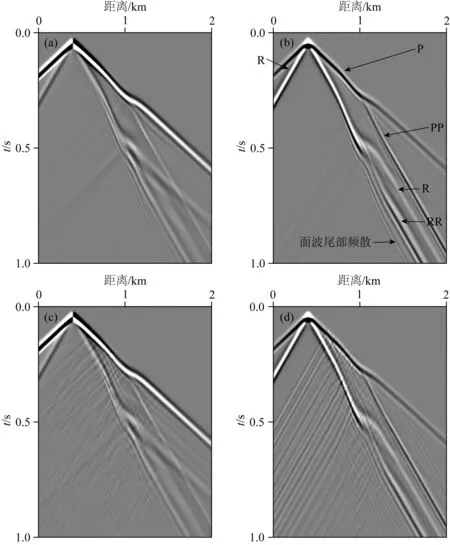
圖14 凸型高斯起伏地表模型QR-RBF-FDM和FDM地震記錄(a) QR-RBF-FDM水平分量; (b) QR-RBF-FDM垂直分量; (c) FDM水平分量; (d) FDM垂直分量.

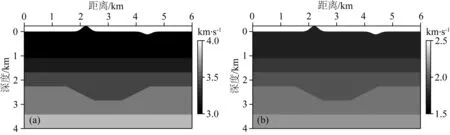
圖16 起伏凹陷模型(a) 縱波速度模型; (b) 橫波速度模型.

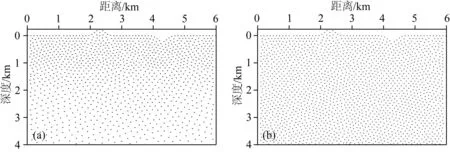
圖17 起伏凹陷模型節點剖分結果(a) 自適應起伏地表節點剖分結果; (b) 常規節點剖分結果.

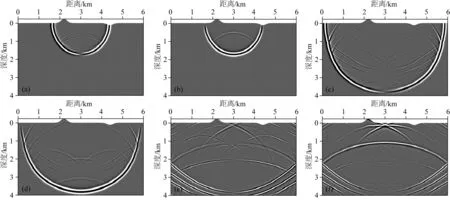
圖18 起伏凹陷模型QR-RBF-FDM波場快照(a) 0.5 s水平分量; (b) 1.0 s水平分量; (c) 1.5 s水平分量; (d) 0.5 s垂直分量; (e) 1.0 s垂直分量; (f) 1.5 s垂直分量.

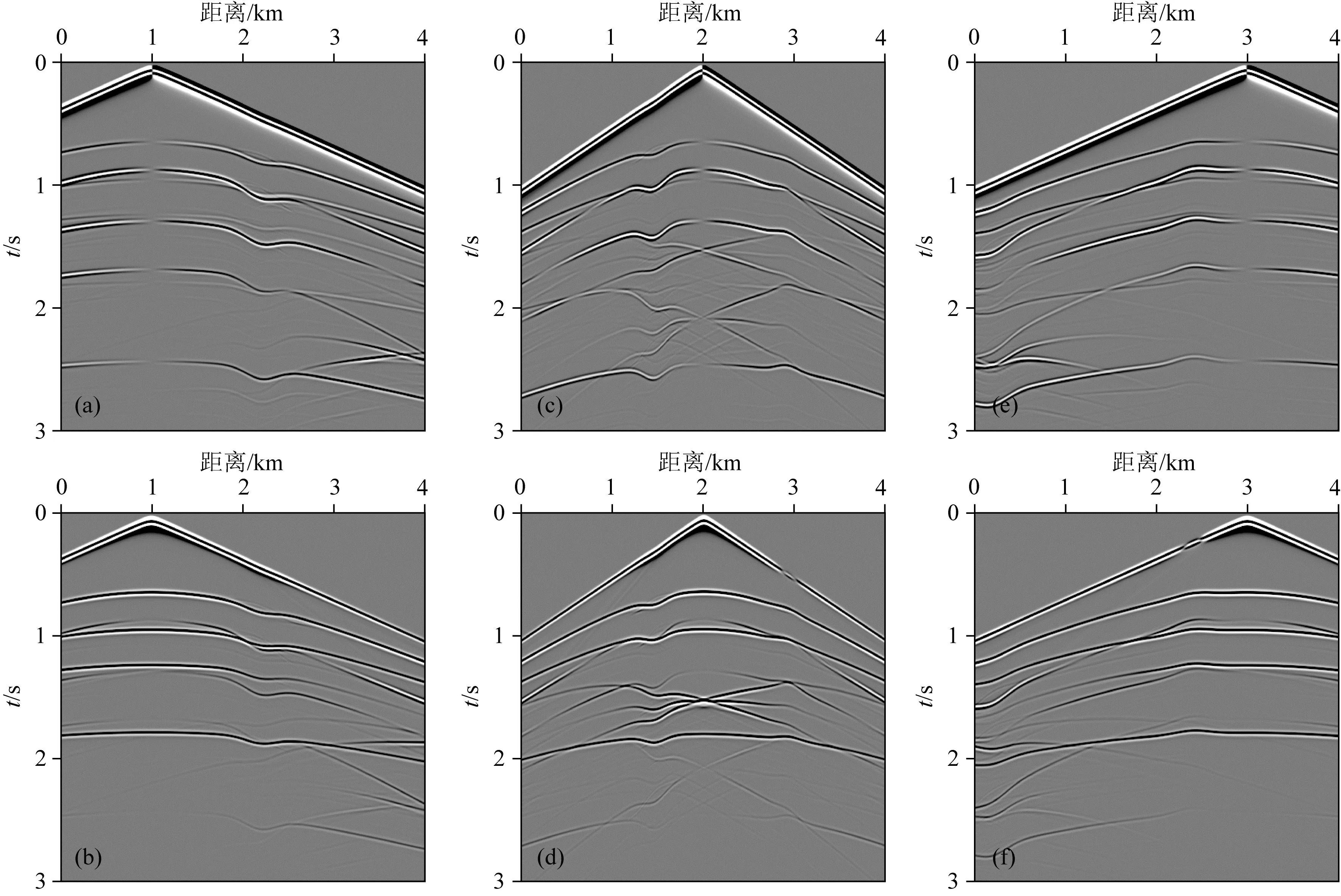
圖19 起伏凹陷模型QR-RBF-FDM地震記錄炮點位于地表1 km：(a)水平分量;(b)垂直分量; 炮點位于地表3 km：(c)水平分量;(d)垂直分量; 炮點位于地表5 km：(e)水平分量;(f)垂直分量.

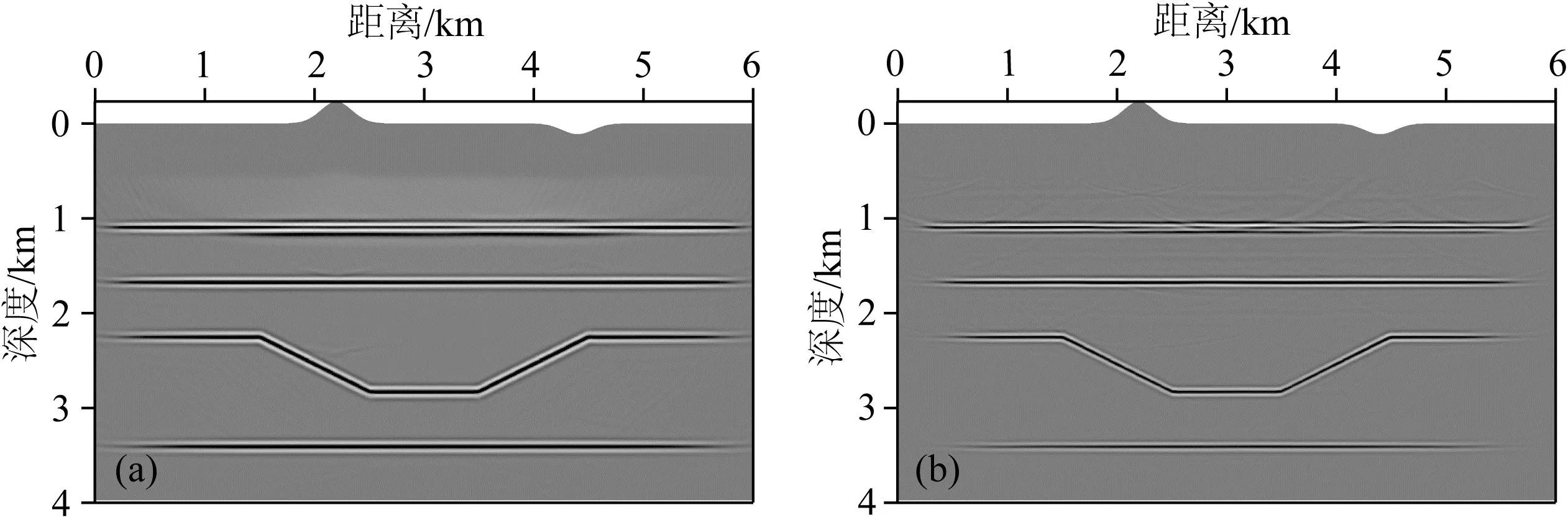
圖20 起伏凹陷模型多炮成像結果(a) PP成像; (b) PS成像.

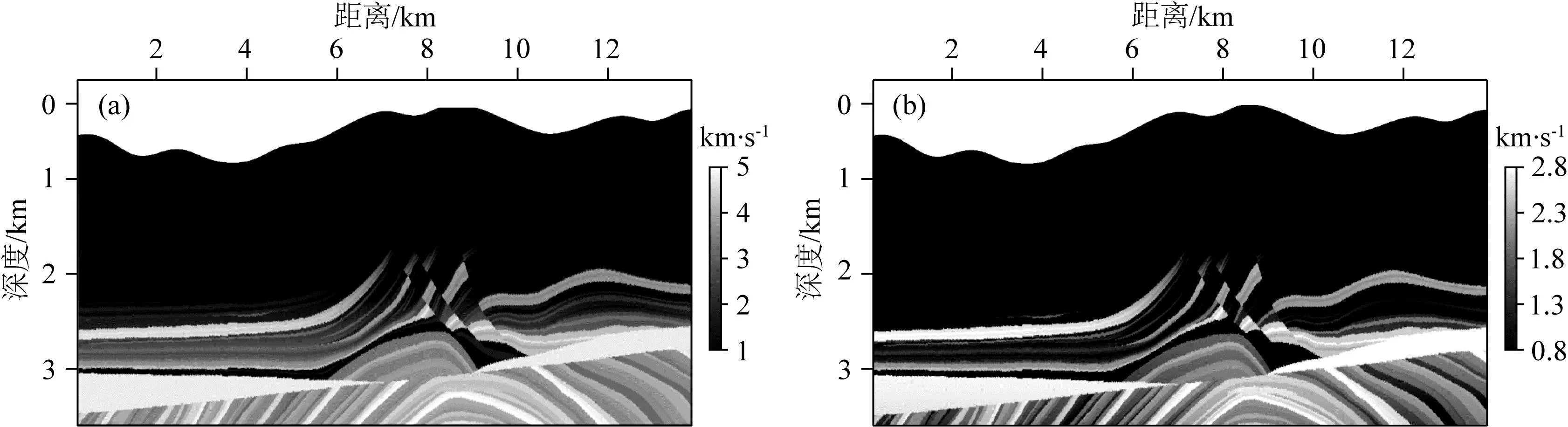
圖21 起伏地表Marmousi-2模型(a) 縱波速度模型; (b) 橫波速度模型.

此處,我們進一步地利用上述方法實現了ERTM,采用60炮主頻20 Hz的雷克子波作為震源時間函數在地表附近放炮,中間激發兩端接收,炮間距100 m.最大記錄時長3 s,每炮400道接收,道間距10 m.圖20給出了多炮疊加后的PP和PS剖面,從中可以看出,QR-RBF-RTM可靈活地處理起伏地表,且地下界面位置準確,同相軸清晰連續,該數值結果驗證了本文方法的正確性.

6.3 起伏地表的Marmousi模型

本節利用經典Marmousi-2模型驗證復雜模型下自適應起伏地表節點剖分法和QR-RBF-FDM的穩定性和適應性,此時地表采用無網格彈性波混合吸收條件.模型見圖21,模型大小為13.6 km×2.8 km,采用Foothill模型的起伏地形作為Marmousi的地形起伏.圖22展示了自適應起伏地表節點剖分法離散的結果.圖22基于自適應起伏地表節點剖分方法中節點間距隨著速度增加而變大,范圍在5～18 m之間.基于該模型進行數值模擬,時間步長為0.5 ms,記錄時間長度為4.5 s,選取主頻為20 Hz的雷克子波作為震源時間函數,檢波點均勻布設于地表,接收范圍為10 km,相鄰檢波點間距為10 m.

圖23給出了不同時刻水平和垂直分量的波場快照,震源位于地表橫向3 km處.圖24為縱橫波分離的波場快照,其中左列為縱波波場分量,右列為橫波波場分量.圖23表明本文方法對于地表高程變化劇烈的復雜地表模型能夠實現高精度數值模擬,圖24表明QR-RBF-FD應用于分離方程能夠有效分離縱橫波.由圖25地震記錄可見,在復雜模型下彈性波場仍然穩定,且無矩形網格剖分引起的虛假反射現象.由圖25的不同炮點位置(地表x方向坐標3.2 km, 6.5 km和9.8 km處)激發的地震記錄可以觀察到,不論在地表任何位置激發的震源,在記錄中均可以清晰地看出,直達波、反射波和轉換波的發育.由于起伏地表的存在,反射波和轉換波的雙曲線特性發生規則扭曲,驗證了在復雜構造和起伏地表情況下QR-RBF-FDM的適應性.

此處,我們進一步地利用上述方法實現了ERTM,采用135炮主頻20 Hz的雷克子波作為震源時間函數在地表附近放炮,中間激發兩端接收,炮間距100 m,最大記錄時長4.5 s,每炮1000道接收,道間距10 m.圖26給出了多炮疊加后的PP和PS成像結果剖面,從中可以看出,成像結果與偏移速度模型的構造界面信息吻合,且地下界面位置準確,無論是PP成像還是PS額成像,同相軸均清晰連續,具有較高的信噪比,表明基于QR-RBF- ERTM方法對起伏地表下得到復雜模型具有良好的適應性.

7 結論

本文提出一種自適應節點剖分法實現起伏地表無網格剖分,在此基礎上提出QRRBF-FDM,推導出彈性波模擬中RBF-FDM的頻散關系和穩定性條件.同時,提出了一種適用于起伏地表的無網格起伏自由地表條件和彈性波混合邊界條件,實現了基于無網格的起伏地表彈性波數值模擬.此外,推導出一種適用于無網格的精確矢量波分離方法,實現了縱橫波分離的無網格彈性波逆時偏移方法.通過對高斯起伏模型,起伏凹陷模型和起伏地表的Marmousi-2模型的數值模擬和偏移試算,得出到以下幾點認識：

(1)自適應節點剖分法不僅能與地表完全匹配,而且節點分布密度隨地下介質的速度變化而變化,在速度大的區域節點分布稀疏,速度小的區域節點分布密集.同時采用自適應節點控制方程對節點位置進行調整,保證節點分布的均勻性.基于該方法,利用無形變參數擾動QR-RBF-FDM進行數值模擬,既保持了傳統FDM的高精度,又彌補了傳統FDM在自由起伏地表處理中缺乏的靈活性的缺點.

(2)在起伏地表條件下,貼體網格與曲網格是模擬地震波的重要方法,其網格易于生成,而且可利用水平地表假設的自由邊界條件,在曲坐標系下直接使用.無網格具有利用彈性波、聲波等方程進行直接差分的優點,無需坐標變換,后期研究中更適用于復雜的黏性介質或各向異性方程.需要指出的是,無網格數值模擬的差分模板仍基于FDM的數值差分思想,其傳播的穩定性依賴于差分模板的均勻性和連續性,因此在現階段仍然無法突破梯度非連續模型,這將是后續研究工作的重點與難點.

(3)基于Gu等(2019)的基礎上,本文推導并實現了無網格模型參數化條件下的起伏地表彈性波逆時偏移.模型試算結果表明,該方法對地表附近和復雜深層成像效果較好,而且震源的干擾效應能準確反演起伏地表形態.

(4)應用QR-RBF-FDM,以無網格模型參數化為基礎,實現逆時偏移,對未來起伏地表復雜構造、復雜介質處理具有廣闊的應用前景;同時,QR-RBF-FDM也可直接應用于最小二乘偏移、全波形反演.

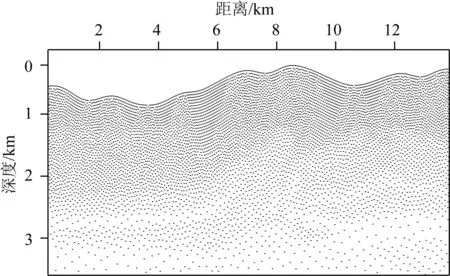
圖22 起伏地表Marmousi-2模型自適應起伏地表節點剖分結果

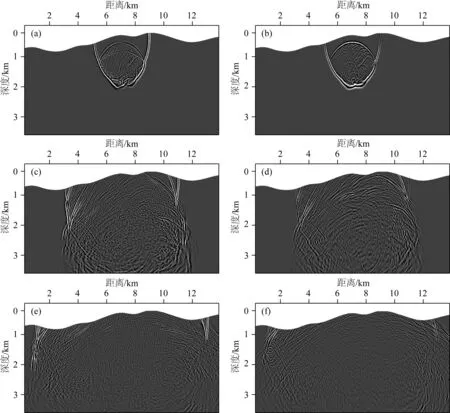
圖23 起伏地表Marmousi-2模型RBF-FDM波場快照(a) 1.0 s水平分量; (b) 1.0 s垂直分量; (c) 2.0 s水平分量; (d) 2.0 s垂直分量; (e) 3.0 s水平分量; (f) 3.0 s垂直分量.

圖24 起伏地表Marmousi-2模型RBF-FDM波場快照(a) 1.0 s縱波分量; (b) 1.0 s橫波分量; (c) 2.0 s縱波分量; (d) 2.0 s橫波分量; (e) 3.0 s縱波分量; (f) 3.0 s橫波分量.

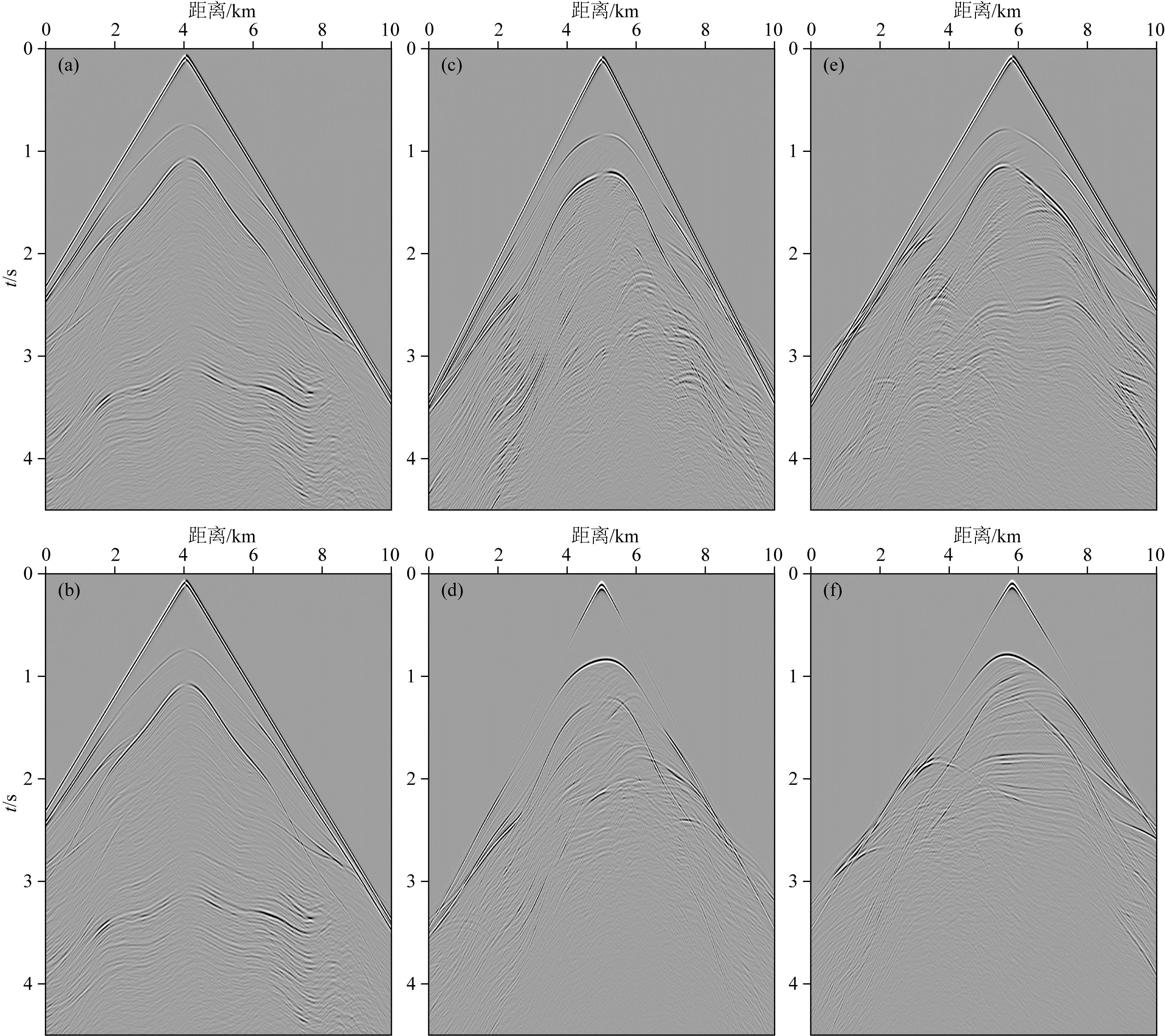
圖25 起伏地表Marmousi-2模型RFB-FDM地震記錄炮點位于地表3.2 km： (a) 水平分量; (b) 垂直分量; 炮點位于地表6.5 km： (c) 水平分量; (d) 垂直分量; 炮點位于地表9.8 km： (e) 水平分量; (f) 垂直分量.

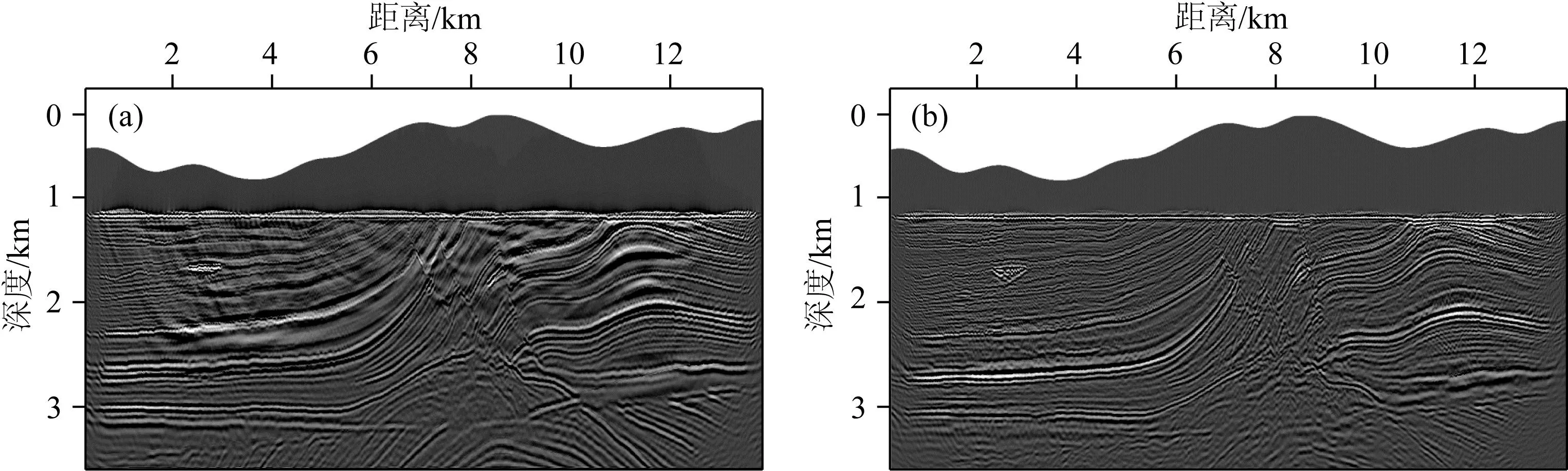
圖26 起伏地表Marmousi-2模型彈性波逆時偏移結果 (a) PP成像; (b) PS成像.