一類非線性Burgers型問題的預測校正緊差分方法

王佳威，張海湘，楊雪花

（湖南工業(yè)大學 理學院，湖南 株洲 412007）

1 研究背景

Burgers 方程是描述許多物理現(xiàn)象的模型方程，如流體力學、非線性聲學、氣體動力學、交通流動力學等。同時，流體動力學中的Naviers-Stokes方程[1-2]忽略壓力項后的簡單數(shù)學模型也可看作Burgers 方程。由于Burgers 方程的重要現(xiàn)實意義，國內外許多學者致力于探討求解Burgers 方程的數(shù)值方法。E.Var?glu 等[3]基于加權殘差公式，提出了一種求解Burgers 方程的有限元方法，精確地求解了不同黏度值的Burgers 方程。J.C.López-Marcos[4]研究了一類非線性偏微分方程，并利用Lubich 卷積求積法[5-6]處理積分項，并給出了收斂性等相關理論證明；Chen H.B.等[7]進一步延伸了文獻[5-6]的結果，運用Lubich 的二階卷積求積公式處理積分項，并且用二階向后差分對時間導數(shù)進行離散，空間則采用二階有限差分格式，對非線性項的處理類似于文獻[4]，得到的結果相對于文獻[4]有明顯的提升。Wang X.P.等[8]對黏性Burgers 方程進行數(shù)值求解，得到了一種無條件穩(wěn)定的緊差分格式；此外，Zhao J.C.[9]提出了以一種具有四階和六階精度的緊差分格式求解一類兩點邊值問題的數(shù)值解，并用數(shù)值算例證明了差分格式的可行性與有效性。Zhou Y.T.等[10]考慮了非線性分數(shù)階Benjamin-Bona-Mahony Burgers 方程的快速二階預測-校正方法，并結合均勻網(wǎng)格上空間導數(shù)的標準離散化，推導了數(shù)值解的離散H1范數(shù)誤差估計。但上述工作多為對經(jīng)典Burgers 型方程的研究，而對廣義非線性Burgers 型方程的研究工作相對較少。

MacCormack 方法[11-13]是R.W.MacCormack 在1969年提出的一種顯式兩步預測-校正算法，該方法分為預測步與校正步，兩步中對空間一階導數(shù)交替使用向前和向后差分。眾多學者將該方法廣泛應用于非線性方程的數(shù)值解中。E.Ngondiep[14]基于MacCormack 方法和Crank-Nicolson 格式求解混合Stokes-Darcy 模型，得到了一種無條件穩(wěn)定的預測-校正差分格式。

本文主要討論下面一類非線性Burgers 方程的預測-校正緊差分格式：

其初始條件和邊界條件如下：

其中核β(t)=tα-1，(x,t)∈(0,1)×(0,T]，α∈(0,1)。

2 預備知識

定義1設α∈R+，φ(t)是I=(0，+∝)上逐段連續(xù)函數(shù)，且在I的子區(qū)間上可積，稱

為函數(shù)φ(t)的α階Riemann-Liouvile（R-L）分數(shù)階積分[15]。

卷積求積公式[5-6]在離散分數(shù)階積分方面具有明顯優(yōu)勢。為了近似Riemann-Liouvile 分數(shù)階積分式（4），下面介紹一階卷積求積公式。

式中k為時間步長。

求積權重

對區(qū)間[0，1]作M等分，區(qū)間[0，T]作N等分，記h=1/M，k=T/N，xj=jh，0≤j≤M，tn=nk，0≤n≤N。其中h為空間步長，k為時間步長。

在結點(xj,tn)上考慮u(x,t)，并記ujn=u(xj,tn)，且定義二階中心差分公式[16-18]為

3 數(shù)值離散格式

3.1 預測-校正差分格式

在結點(xj,tn)上考慮定解問題（1）～（3），有

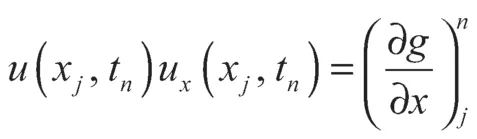
式中r=kα+1。

校正步表達式為

邊界條件為

初值條件為

3.2 預測-校正緊差分格式

在建立時間半離散格式（9）的緊差分格式前，首先給出具有四階精度的一階導數(shù)緊差分公式以及二階導數(shù)緊差分公式。

舍去截斷誤差o(h4)，整理可得以下二階導數(shù)的緊差分公式：

當j=M-1 時，有

式（11）（12）的截斷誤差都為o(h4)，且式中系數(shù)可由泰勒公式以及待定系數(shù)法確定。

記

則可將式（10）～（12）寫成如下矩陣形式

式（14）的截斷誤差為o(h4)，同理，為了求解一階導數(shù)在邊界處（j=1，M-1）的值，調整邊界處的緊致差分公式。

當j=1 時，有

當j=M-1 時，有

式（15）（16）的截斷誤差也為o(h4)，且式中系數(shù)可由泰勒公式以及待定系數(shù)法確定。記

可將式（8）～（10）改寫成如下矩陣形式

式（13）（17）即分別為矩陣的一階導數(shù)緊差分公式以及二階導數(shù)緊差分公式。

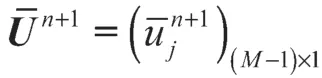
由式（17）可得

由式（13）可得

將式（19）（20）代入式（18），并結合初邊值條件，可得到如下Euler 預測-校正緊差分格式

4 數(shù)值算例

應用Euler 預測-校正緊差分格式計算下列定解問題

其中精確解為

右端項為

不同步長時數(shù)值解和精確解最大誤差為

空間收斂階為

其中b/a為空間步長比；

時間收斂階為

固定時間步長N=300 000，對α進行不同取值時，差分格式的最大誤差以及空間收斂階與參數(shù)M的關系如表1所示。由表1 可以得知，空間收斂階在4 附近波動。

表1 N=300 000 時x 方向最大誤差及空間收斂階與參數(shù)M 的關系Table 1 Maximum error in x direction and the relationship between spatial order and parameter M with N=300 000

固定空間步數(shù)M=32，對α進行不同取值時，不同α下差分格式的最大誤差以及時間收斂階與參數(shù)N的關系如表2所示。由表2 可以得知，時間收斂階約為一階。

表2 M=32 時t 方向最大誤差及時間收斂階與參數(shù)N 的關系Table 2 Maximum error in t direction and the relationship between time order and parameter N with M=32

固定α=0.50，則t=0.5 時的數(shù)值解與精確解的對比曲線（h=1/10，k=1/8 000）如圖1所示；α=0.50，x=0.25 時的數(shù)值解與精確解的對比曲線（h=1/8，k=1/64）如圖2所示。由圖1 和2 可以看出，數(shù)值解與精確解較為吻合。

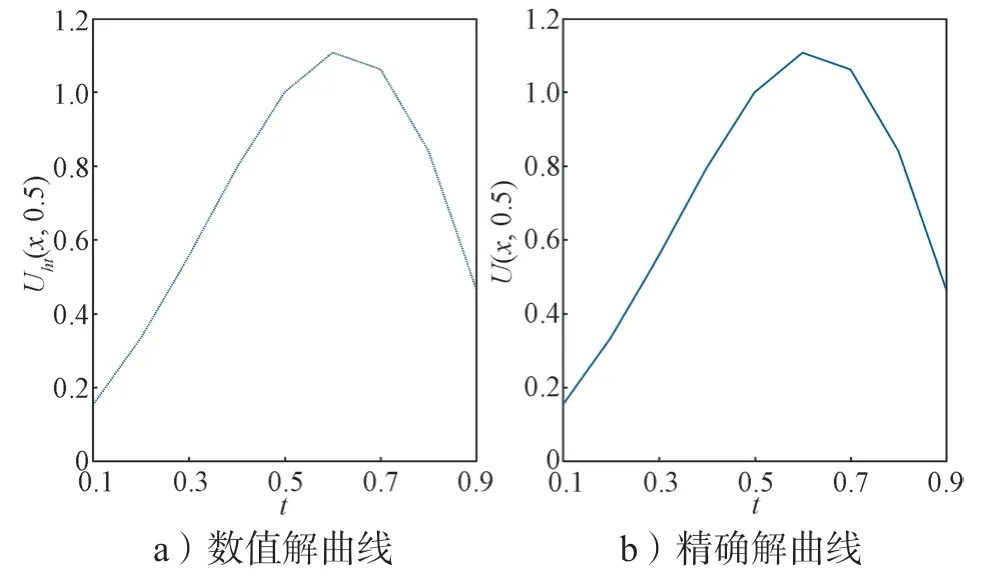
圖1 α=0.50,t=0.5 時數(shù)值解與精確解曲線Fig.1 Curves of numerical and exact solutions with α=0.50,t=0.5

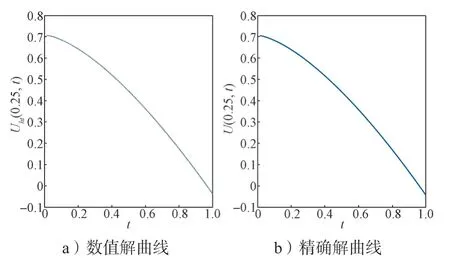
圖2 α=0.50,x=0.25 時數(shù)值解與精確解曲線Fig.2 Curves of numerical and exact solutions with α=0.50,x=0.25

固定α=0.50，則t=0.50 時不同空間步長的數(shù)值解與精確解的絕對誤差對比曲線如圖3所示，由圖可以得知，空間步長越小，其數(shù)值解與精確解的絕對誤差越小。

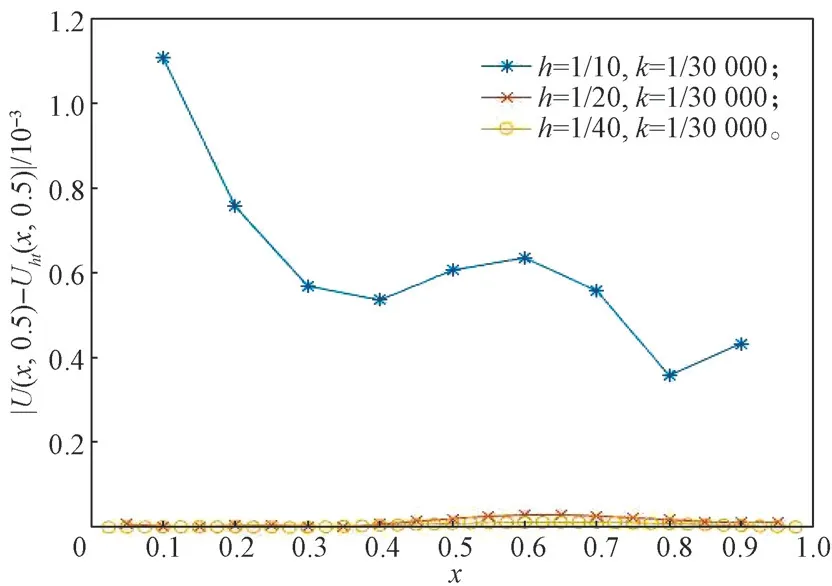
圖3 α=0.50,t=0.5 時不同空間步長數(shù)值解與精確解的絕對誤差曲線Fig.3 Absolute error curves of numerical and exact solutions for different spatial steps with α=0.50,t=0.5

圖4 給出了當α=0.50，x=0.25 時，不同時間步長的數(shù)值解與精確解的絕對誤差對比曲線，由圖4 可以看出，時間步長越小，數(shù)值解與精確解的絕對誤差也越小。

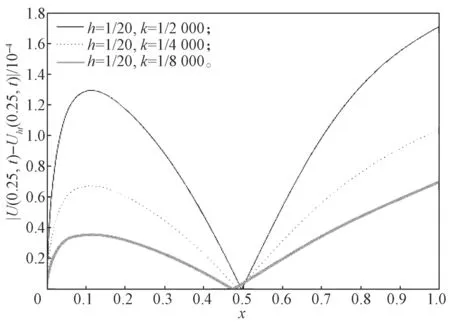
圖4 α=0.50,x=0.25 時不同時間步長數(shù)值解與精確解的絕對誤差曲線Fig.4 Absolute error curves of numerical and exact solutions at different time steps with α=0.50,x=0.25

圖5 給出了α=0.50，h=1/20，k=1/4 000 時的數(shù)值解與精確解的絕對誤差曲面。由圖5 可看出，數(shù)值解與精確解的絕對誤差數(shù)量級比較小，說明數(shù)值解與精確解比較吻合。

圖5 α=0.50 時數(shù)值解與精確解的絕對誤差曲面(h=1/20,k=1/4 000)Fig.5 Absolute error surface of numerical solution and exact solutions with α=0.50(h=1/20,k=1/4 000)

5 結語

本文研究了一類非線性Burgers 方程的預測-校正緊差分格式，基于矩陣的一階導數(shù)和二階導數(shù)的緊差分公式，以及MacCormack 預測-校正方法，建立了Euler 預測-校正緊差分格式。由數(shù)值算例結果可知本文考慮的Euler 預測-校正緊差分格式的收斂階為o(k+h4)，且最大誤差隨著剖分數(shù)增大而減小。