利用對角線證明中點四邊形的特殊性

陳禮弦

(貴州省貴安新區普貢中學,貴州 貴陽 561113)

任意畫一個四邊形,以這個四邊形各邊的中點為頂點可以組成一個新的四邊形,這個新的四邊形叫做中點四邊形[1].中點四邊形有何特殊性,教師又如何去引導學生證明呢?教學實踐發現,這是一個數學模型,利用已知四邊形的對角線證明中點四邊形的性質,會達到事半功倍的效果.

1 基本模型

模型1 已知四邊形的對角線既不相等也不垂直,中點四邊形是平行四邊形

如圖1,已知四邊形ABCD,點E,F,G,H分別是AB,BC,CD,AD的中點,問四邊形EFGH是什么四邊形?說明理由.

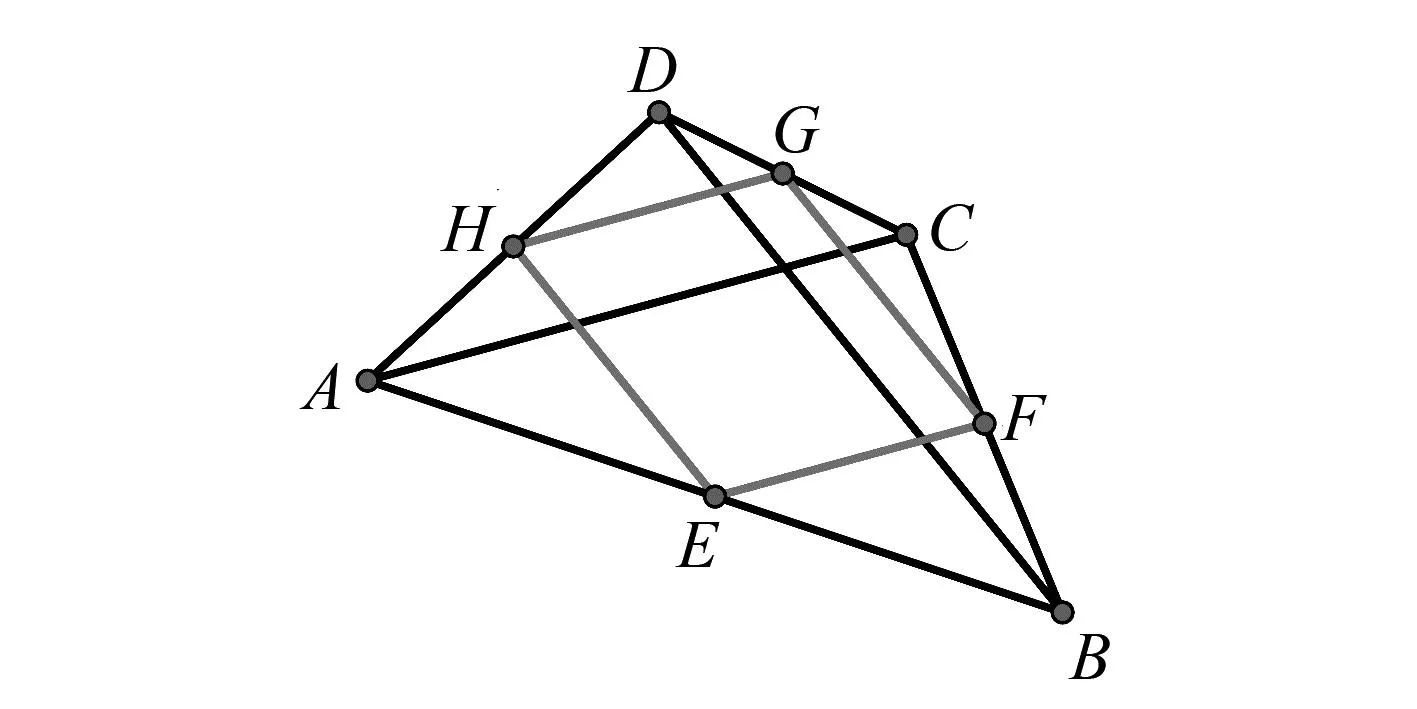
圖1 模型1圖

模型分析:由三角形中位線的性質,易知四邊形EFGH是平行四邊形.理由如下:

因為點E,F,G,H分別是AB,BC,CD,AD的中點,由三角形中位線的性質可得EH∥BD,BD=2EH,FG∥BD,BD=2FG,所以EH∥FG,EH=FG,所以四邊形EFGH是平行四邊形.

模型2 已知四邊形的對角線相等,但不垂直,中點四邊形是菱形

如圖2,已知四邊形ABCD,點E,F,G,H分別是AB,BC,CD,AD的中點,AC=BD,問四邊形EFGH是什么四邊形?說明理由.

模型分析:四邊形EFGH是菱形.理由如下:

因為點E,F,G,H分別是AB,BC,CD,AD的中點,所以EH∥BD,BD=2EH,FG∥BD,BD=2FG,EF∥AC,AC=2EF,所以EH∥FG,EH=FG,所以四邊形EFGH是平行四邊形.又AC=BD,所以EF=EH,所以四邊形EFGH是菱形.

模型3 已知四邊形的對角線垂直,但是不相等,中點四邊形是矩形

如圖3,已知四邊形ABCD,點E,F,G,H分別是AB,BC,CD,AD的中點,AC⊥BD,問四邊形EFGH是什么四邊形?說明理由.

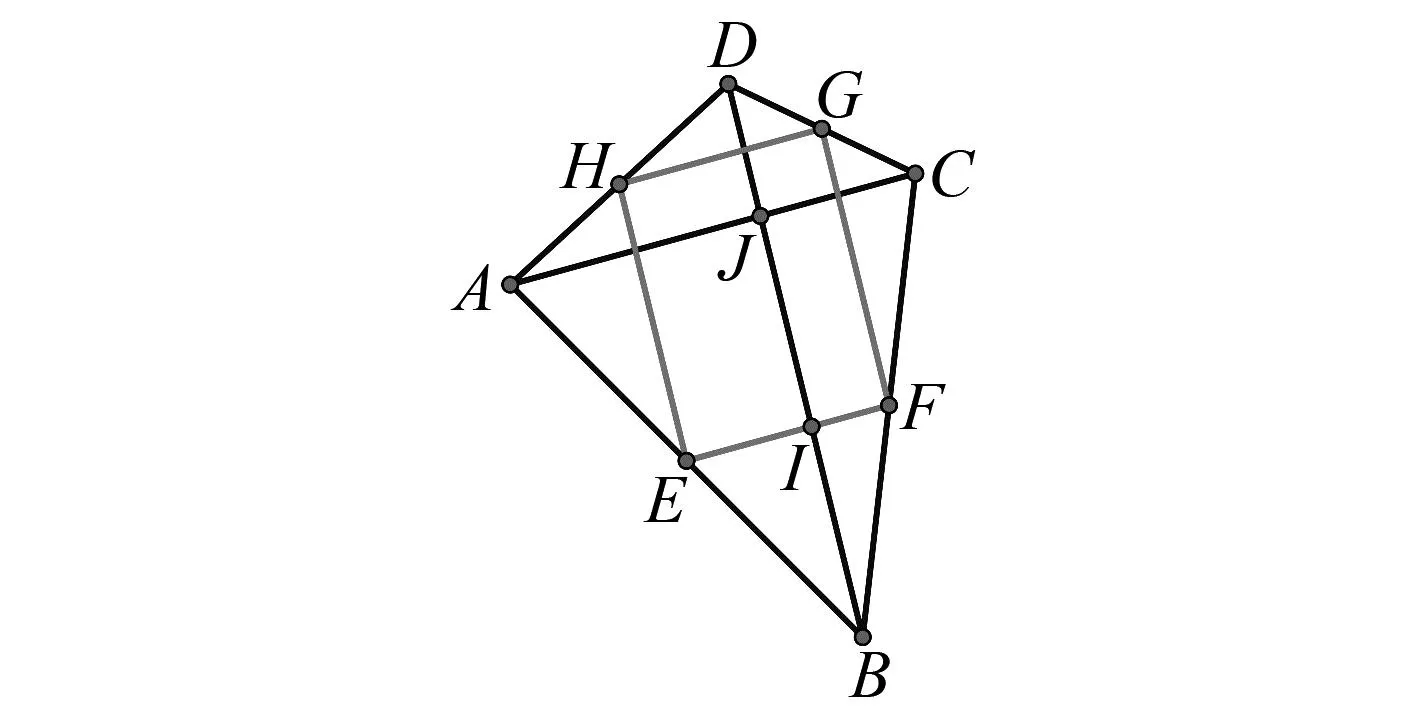
圖3 模型3圖

模型分析:四邊形EFGH是矩形.理由如下:

因為點E,F,G,H分別是AB,BC,CD,AD的中點,所以EH∥BD,BD=2EH,FG∥BD,BD=2FG,EF∥AC,AC=2EF,所以EH∥FG,EH=FG,所以四邊形EFGH是平行四邊形,又因為AC⊥BD,所以∠AJD=90°,所以∠EFG=∠EID=∠AJD=90°,所以四邊形EFGH是矩形.

模型4 已知四邊形的對角線既相等又垂直,中點四邊形是正方形

如圖4,已知四邊形ABCD,點E,F,G,H分別是AB,BC,CD,AD的中點,AC=BD,AC⊥BD,問四邊形EFGH是什么四邊形?說明理由.

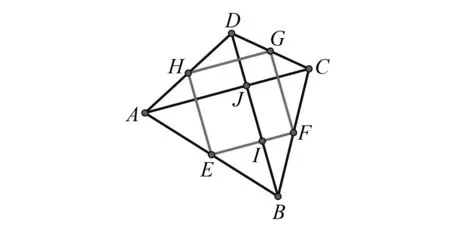
圖4 模型4圖

模型分析:四邊形EFGH是正方形.理由如下:

因為點E,F,G,H分別是AB,BC,CD,AD的中點,所以EH∥BD,BD=2EH,FG∥BD,BD=2FG,EF∥AC,AC=2EF,所以EH∥FG,EH=FG,所以四邊形EFGH是平行四邊形.又因為AC⊥BD,所以∠AJD=90°,所以∠EFG=∠EID=∠AJD=90°,所以四邊形EFGH是矩形.又因為AC=BD,所以EF=EH,所以四邊形EFGH是菱形,所以四邊形EFGH是正方形.

2 應用例舉

例1 如圖5,四邊形MNOP中,I,J,K,L分別是MN,NO,OP,PM的中點,若四邊形IJKL是菱形,那么四邊形MNOP的對角線滿足什么條件?

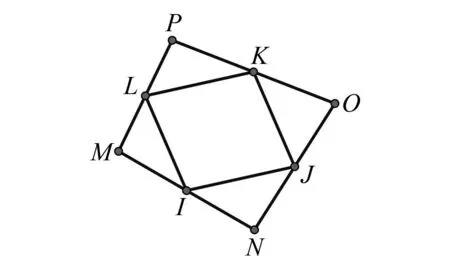
圖5 例1題圖

解析根據模型1,易知四邊形IJKL是平行四邊形.又因為若四邊形IJKL是菱形,根據模型2,易知四邊形MNOP的對角線相等,所以若四邊形IJKL是菱形,所以四邊形MNOP的對角線滿足的條件是MO=PN.

例2 如圖6,四邊形DEFG是菱形,點H,I,J,K分別是邊DE,EF,FG,GD的中點,請問四邊形HIJK是什么圖形?

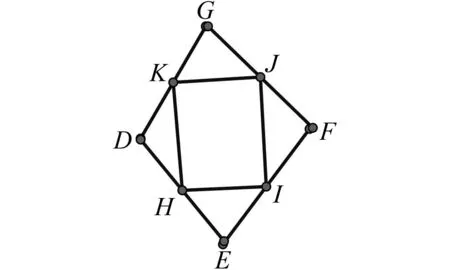
圖6 例2題圖

解析因為四邊形DEFG是菱形,所以四邊形DEFG對角線互相垂直.根據模型3,易知四邊形DEFG是矩形.

例3 如圖7,在四邊形BCDE中,F、J、H、I分別是各邊的中點,則四邊形FJHI是( ).

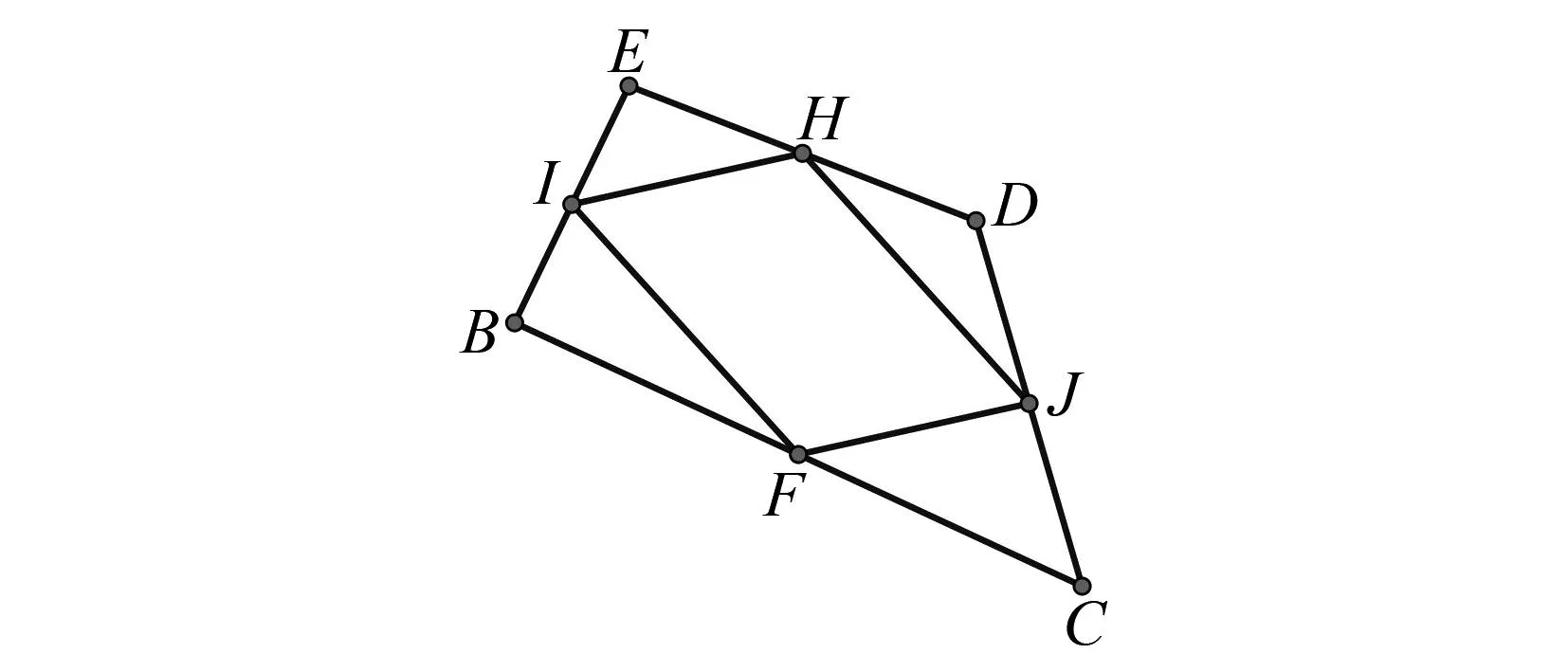
圖7 例3題圖

A. 正方形 B.矩形

C.菱形 D.平行四邊形

解析因為在四邊形BCDE中,F、J、H、I分別是各邊的中點,根據模型1,易知四邊形FJHI是平行四邊形,故選D.

例4 如圖8,點G、H、I、J分別是四邊形CDEF的邊CD、DE、EF、FC的中點,若四邊形GHIJ是矩形,則四邊形CDEF的對角線CE和DF有何關系?

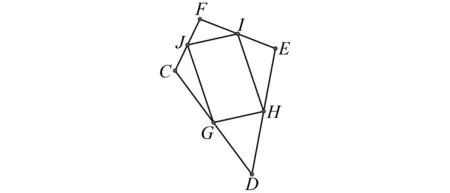
圖8 例4題圖

解析因為點G、H、I、J分別是四邊形CDEF的邊CD、DE、EF、FC的中點,四邊形GHIJ是矩形,根據模型3,易知四邊形CDEF的對角線CE和DF互相垂直,即CE⊥DF.

例5 如圖9,四邊形EFGH四條邊上的中點分別為I、J、K、M,順次連接點I、J,K、M,得到四邊形IJKM.

圖9 例5題圖

(1)四邊形IJKM的形狀是________.當四邊形EFGH的對角線滿足____(填入位置關系或數量關系)時,四邊形IJKM是矩形.

(2)當EG=FH時,四邊形IJKM的形狀是____.

(3)若EG⊥FH且EG=FH,求證:四邊形IJKM為正方形.

解析(1)因為四邊形EFGH四條邊上的中點分別為I、J、K、M,根據模型1,易知四邊形IJKM是平行四邊形.根據模型3,易知四邊形EFGH的對角線滿足EG⊥FH.故四邊形IJKM是平行四邊形,EG⊥FH.

(2)因為四邊形EFGH對角線EG=FH,根據模型2,易知四邊形IJKM是菱形.

(3)證明:因為四邊形EFGH對角線EG⊥FH.根據模型3,四邊形IJKM是矩形,又因為四邊形EFGH對角線EG=FH,根據模型2,四邊形IJKM菱形.綜上所述,四邊形IJKM是正方形.

3 結束語

綜上所述,不論已知四邊形是什么四邊形,其中點四邊形的形狀只與已知四邊形的兩條對角線有關.當已知四邊形的兩條對角線既不相等也不垂直時,順次連接已知四邊形各邊的中點得到的中點四邊形是平行四邊形;當已知四邊形的兩條對角線相等,但是不垂直時,順次連接已知四邊形各邊的中點得到的中點四邊形是菱形;當已知四邊形的兩條對角線垂直,但是不相等時,順次連接已知四邊形各邊的中點得到的中點四邊形是矩形;當已知四邊形的兩條對角線既相等又垂直時,順次連接已知四邊形各邊的中點得到的中點四邊形是正方形[2].中點四邊形的這些特殊性在解題中有著廣泛的應用.