集輸管道臨界攜液流速計算模型研究

秦 虹，趙紫汐，姚佳杉，許開志，李 盼

1.中國石油華北油田公司第一采油廠，河北任丘 062552

2.中國石油華北油田公司第二采油廠，河北霸州 065700

3.中國石油華北油田公司第五采油廠，河北辛集 052360

目前，我國天然氣、煤層氣或伴生氣的集輸普遍采用氣液混輸（濕氣輸送）的方式。雖然在部分井場的井口裝備了氣液分離裝置，但受管內(nèi)溫度、壓力的影響，在一些低洼處仍不可避免地形成凝析液或水[1]。特別是近年來，我國油氣資源逐漸從內(nèi)陸向海洋、山區(qū)和沙漠發(fā)展，地形起伏帶來的管內(nèi)積液問題頻繁發(fā)生，導(dǎo)致管道壓降增大、低洼處腐蝕嚴(yán)重和下游設(shè)備頻繁起跳等問題[2]。因此，研究氣液混輸過程中流體流動特性，分析起伏管道積液的形成原因和規(guī)律，對指導(dǎo)集輸管道的設(shè)計及安全運(yùn)行具有重要意義。

迄今，諸多學(xué)者已在地面集輸管道的積液、壓降或臨界攜液流速等方面進(jìn)行了研究，劉曉倩等[3]研究了氣體流速、管道傾角對管內(nèi)持液率的影響，獲得了不發(fā)生積液的臨界傾角，但測試的傾角范圍僅為-4°～4°，現(xiàn)場應(yīng)用范圍較小；陳建磊等[4]利用Wallis 提出的液泛公式作為臨界攜液流速的修正公式，但模型忽略了液相表觀流速，且未經(jīng)過現(xiàn)場驗(yàn)證。基于上述問題，基于多相流OLGA 軟件和雙流體模型確定了臨界攜液流速的預(yù)測方法，并模擬不同影響因素下的臨界攜液流速，進(jìn)而通過均勻?qū)嶒?yàn)設(shè)計獲取因素間的交互作用強(qiáng)度，最后通過隨機(jī)森林模型完成非線性數(shù)據(jù)回歸，并針對現(xiàn)場氣井參數(shù)與文獻(xiàn)中的模型方法進(jìn)行對比。

1 臨界攜液流速預(yù)測方法研究

關(guān)于臨界攜液流速的預(yù)測方法有零液壁剪切應(yīng)力模型、最小界面剪切應(yīng)力模型、最小壓降梯度模型和最小持液率模型等[5-6]。其中，王旭等[7]在實(shí)驗(yàn)中證明了以液滴或液膜反轉(zhuǎn)作為產(chǎn)生積液的時機(jī)較實(shí)際時間偏早，Adewumi 等[8]證明了某些濕氣管道在經(jīng)過分離器分離后仍存在低液相負(fù)荷流動，說明前兩個模型的適應(yīng)性有待進(jìn)一步驗(yàn)證。Landman等[9]證明在近水平的氣液兩相流動過程中，如僅改變氣相流量，則通過動量方程計算出的持液率可能存在中間解不穩(wěn)定的現(xiàn)象，特別當(dāng)管道傾角較大或液相負(fù)荷較大時，持液率的結(jié)果不可靠。最小壓降模型是指當(dāng)管內(nèi)壓降梯度最小時，摩阻損失由重力壓降向摩阻壓降轉(zhuǎn)變的時機(jī)下，管內(nèi)積液最小，Belt[10]、Fan 等[11]均支持該模型。綜上，后續(xù)通過最小壓降梯度模型確定臨界攜液流速。

對某氣田的管道傾角進(jìn)行統(tǒng)計分析，發(fā)現(xiàn)傾角基本分布在0°～30°，當(dāng)氣液流經(jīng)下傾管段時，重力作用將加速液相流動，形成分層流，下傾管段的持液率較低，因此積液主要分布在低洼上坡管段，故后續(xù)研究對象以上傾管段為主。在OLGA 軟件中建立上傾管段模型，管道水平長度1 km，通過改變天然氣質(zhì)量流量，確定井口溫度、系統(tǒng)壓力、管徑、上傾角、含水率、管壁粗糙度等因素下的臨界攜液流速，氣質(zhì)組分見表1。

表1 氣質(zhì)組分摩爾分?jǐn)?shù) 單位：%

實(shí)驗(yàn)條件（見表2）與現(xiàn)場工況一致，表2 中的紅色加粗字體為單因素分析中的固定因素。

表2 實(shí)驗(yàn)條件

在固定因素下，應(yīng)用雙流體模型對上傾管段進(jìn)行水力和熱力計算，該模型的核心是求解質(zhì)量守恒、動量守恒和能量守恒的微分方程，進(jìn)而獲得閉合剪切應(yīng)力、局部流速和流型等瞬態(tài)流動特性，據(jù)此查看不同氣量下的壓降梯度和持液率變化，見圖1。兩相流動的總壓降由加速壓降、重力壓降和摩擦壓降組成，其中加速壓降與其余兩項(xiàng)相比，可以忽略不計。在氣量較小時，液相所受的重力分量和液相與管壁的摩擦力之和大于氣相曳力，氣相流速難以克服阻力影響將液相從低洼處攜出，此時管內(nèi)重力壓降占主導(dǎo)地位；隨著氣量的進(jìn)一步增大，氣相流速產(chǎn)生的曳力足以克服阻力，液層產(chǎn)生的波紋變稠密，上傾段液相平鋪長度增加，液相回流量減少，直到液相不再回流，流動方向與氣相流動方向相同，此時管內(nèi)的總壓降梯度降至最小，壓降仍以重力壓降為主，但摩擦壓降的比重逐漸上升；之后，氣相流量繼續(xù)增大，液相逐漸被帶出上傾管段，管內(nèi)持液率繼續(xù)下降，下降程度較之前有所減緩，說明要想讓管內(nèi)的積液達(dá)到完全排出的程度需要較大的氣相流速，此時總壓降逐漸增大。以上模擬結(jié)果也從側(cè)面證明了采用最小持液率模型判斷臨界攜液流速具有較強(qiáng)的保守性，最小壓降梯度對應(yīng)的氣體流量為1 290 kg/h，臨界攜液流速為3.57 m/s。

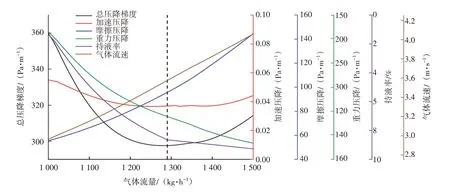
圖1 上傾管段不同氣量下的壓降梯度和持液率變化

2 單因素影響分析

2.1 系統(tǒng)壓力和井口溫度

在表2 給出的條件下，分析系統(tǒng)壓力和井口溫度變化對臨界攜液流速的影響，見圖2。在溫度一定的條件下，系統(tǒng)壓力對液相的影響較小，根據(jù)氣體狀態(tài)方程，系統(tǒng)壓力與氣相密度呈正比，壓力越大，氣相密度越大，氣液兩相間的摩擦、碰撞和剪切作用增強(qiáng)，氣體攜液能力增強(qiáng)，臨界攜液流速變小，但降低幅度逐漸減小，兩者呈冪函數(shù)關(guān)系。在壓力一定的條件下，井口溫度增加，氣相和液相黏度降低，但溫度對液相黏度的影響更大，導(dǎo)致氣體可攜帶的液膜厚度變小，氣體攜液能力變?nèi)酰R界攜液流速變大，兩者呈線性正相關(guān)。

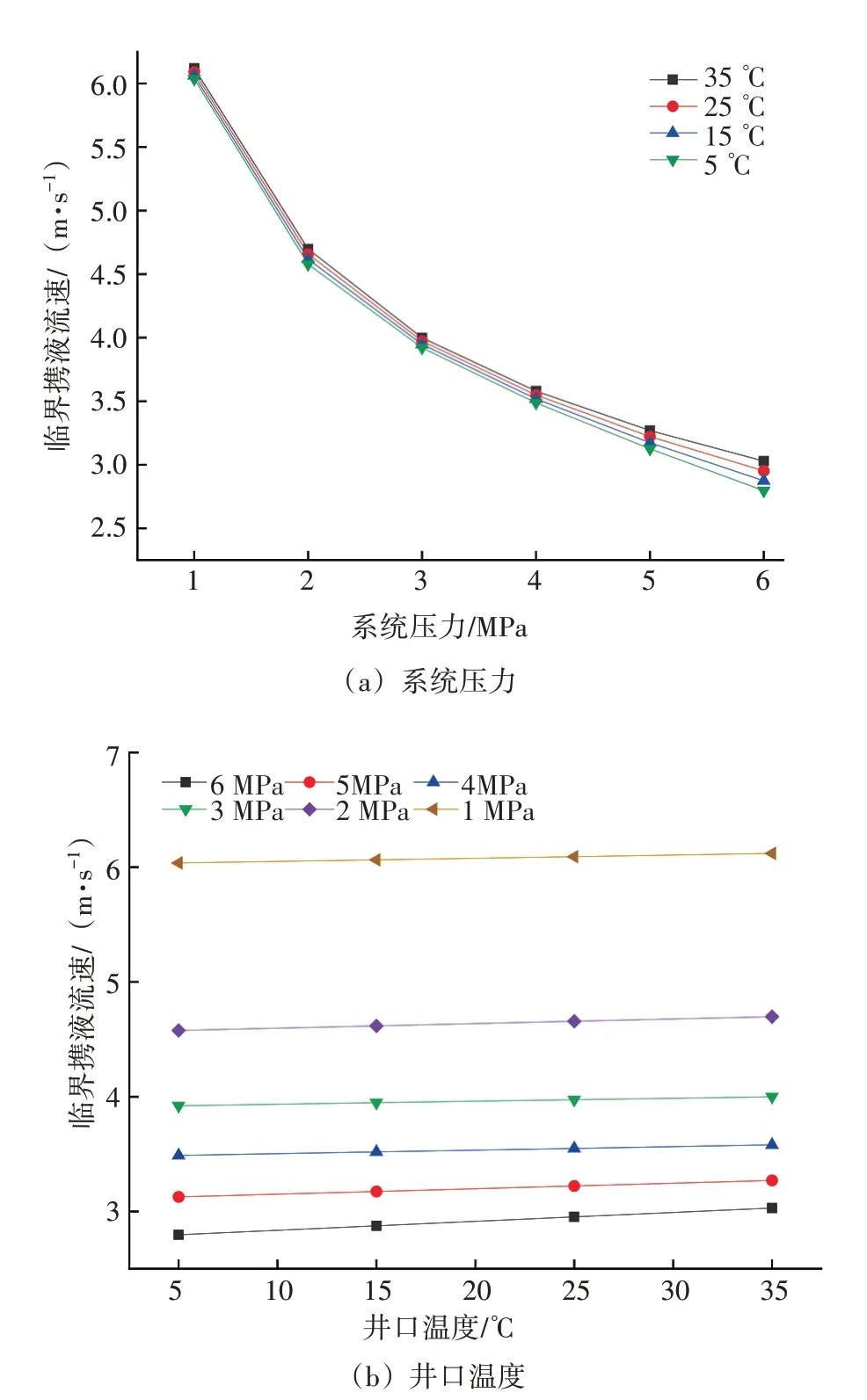
圖2 系統(tǒng)壓力和井口溫度變化對臨界攜液流速的影響

2.2 管徑和傾角

在表2 的條件下，分析管徑和傾角變化對臨界攜液流速的影響，見圖3。隨著管徑增大，氣液流動面積增大，兩相之間的剪切作用減弱，為達(dá)到之前的攜液效果，需增大臨界攜液流速，兩者呈線性正相關(guān)。隨著傾角增大，積液在上傾管段受到的重力分量不斷增大，持液率減小，此時氣體要達(dá)到之前的局部流速需提高氣體流速，且液膜沿管道內(nèi)壁周向的分布更加均勻，綜合作用下氣體攜液所需的能量增加，臨界攜液流速呈先快速增加后緩慢增加，兩者呈對數(shù)關(guān)系。這與Belfroid等[12]提出的臨界攜液氣速與管道傾角呈正弦分布的結(jié)果基本一致（文獻(xiàn)中的傾角范圍為0°～90°）。

圖3 管徑和傾角變化對臨界攜液流速的影響

2.3 含水率和管壁粗糙度

在表2 的條件下，分析含水率和管壁粗糙度對臨界攜液流速的影響，見圖4。隨著體積含水率的增加，管內(nèi)游離水和凝析液的含量增加，臨界攜液流速增大，但在含水率超過10%之后，臨界攜液流速的變化變小。以傾角10°為例，臨界攜液流速與含水率呈對數(shù)關(guān)系。隨著管壁粗糙度的增加，氣壁和液壁之間的剪切應(yīng)用也增大，使積液變得困難，臨界攜液流速減小，兩者呈線性負(fù)相關(guān)。此外，結(jié)合圖3、圖4，在相同的管徑、含水率和管壁粗糙度的情況下，傾角越大，臨界攜液流速的變化越小，傾角大于20°時，其余因素對臨界攜液流速的影響較小。

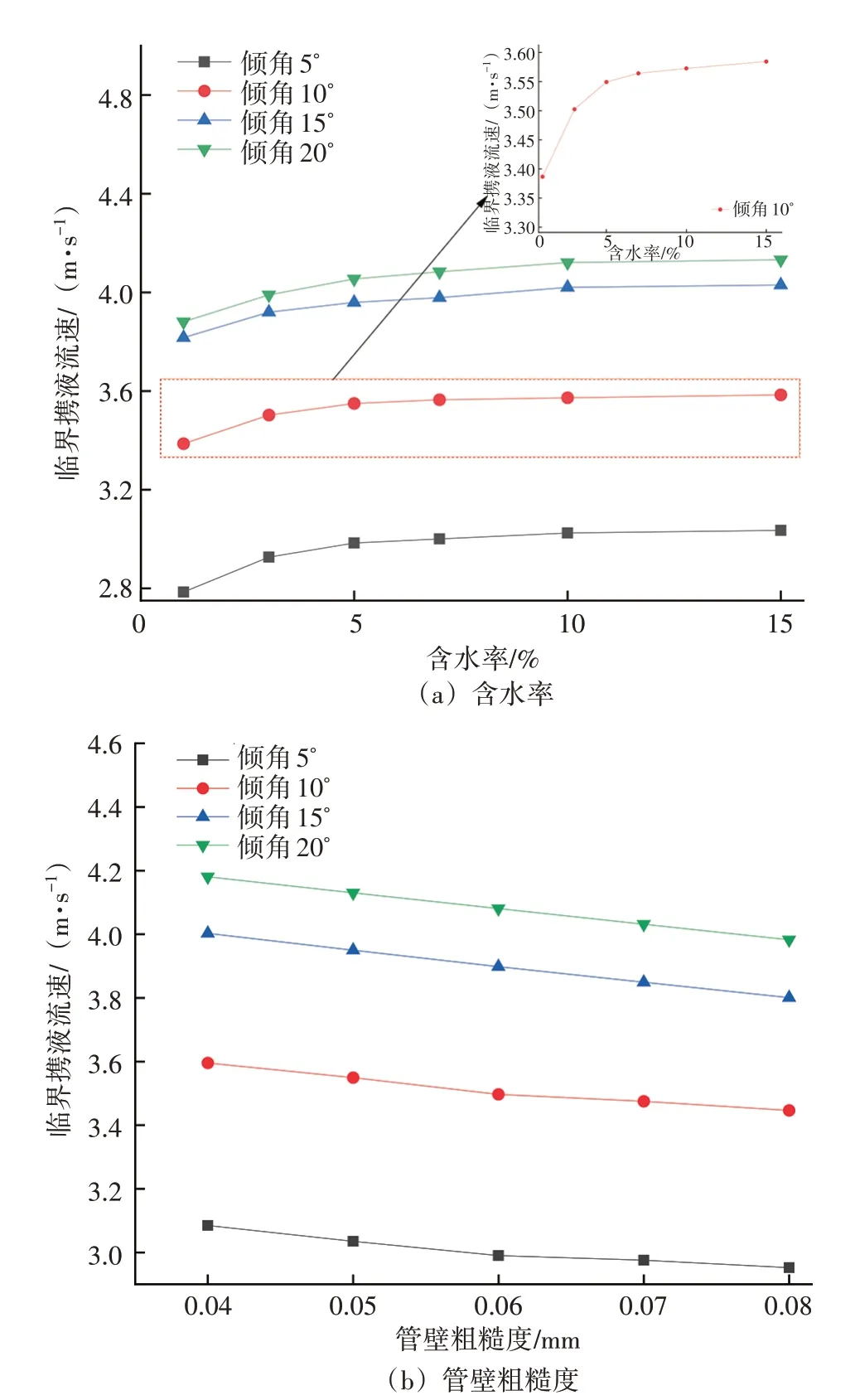
圖4 含水率和管壁粗糙度變化對臨界攜液流速的影響

3 交互作用影響分析

以上傾角因素的8 個水平為基礎(chǔ)對其余因素的水平進(jìn)行擴(kuò)充，形成6 因素、8 水平的均勻?qū)嶒?yàn)設(shè)計，以此獲取不同因素之間的交互作用強(qiáng)度。考慮到每次的實(shí)驗(yàn)設(shè)計表頭形式不一，通過多次迭代，取各項(xiàng)偏差最小的實(shí)驗(yàn)方案，最終中心化偏差為0.271 7，L2偏差為0.033 0，修正偏差為0.420 4，可卷偏差為0.552 4，實(shí)驗(yàn)結(jié)果見表3。

表3 實(shí)驗(yàn)結(jié)果

通過不斷增加變量，對模型進(jìn)行二次多項(xiàng)式逐步回歸，得到的二次模型中F值為15 838.73，p值為0.006 1，調(diào)整后的相關(guān)系數(shù)為0.999 89，說明均勻?qū)嶒?yàn)設(shè)計方案合理，結(jié)果具有可信性。偏回歸系數(shù)的檢驗(yàn)結(jié)果見表4，t檢驗(yàn)的絕對值越大，則該因素越重要。單因素中上傾角對臨界攜液流速的影響最大，其次為含水率和系統(tǒng)壓力，其余未展示因素對臨界攜液流速的影響不顯著；二次項(xiàng)因素中，系統(tǒng)壓力和上傾角的交互作用最強(qiáng)，其次為管徑和含水率的交互作用；表4中的p值均小于0.01，說明所列因素對結(jié)果的影響極其顯著。

表4 偏回歸系數(shù)的檢驗(yàn)結(jié)果

4 模型建立與數(shù)據(jù)預(yù)測

以往以液泛經(jīng)驗(yàn)公式為基礎(chǔ)的優(yōu)化模型通常只考慮氣液表觀流速、傾角和氣液密度等對臨界攜液流速的影響，但從前述分析可知，影響因素之間還存在較強(qiáng)的交互作用，因此以往模型從機(jī)理上不具備廣泛適用性。在此，采用基于集群策略和改進(jìn)決策樹為基礎(chǔ)的隨機(jī)森林模型對本文第2、3 章的數(shù)據(jù)進(jìn)行回歸，共計148 組數(shù)據(jù)，按照8:2 的比例隨機(jī)抽取形成訓(xùn)練集和預(yù)測集，數(shù)據(jù)量分別為118組和30組。首先，通過Bootstrap方式對訓(xùn)練集進(jìn)行有放回的抽樣，隨機(jī)抽取{X1,X2,…,Xn}共n個樣本集；其次，隨機(jī)抽取m個特征變量作為當(dāng)前決策樹的分裂特征集（m小于等于原始特征變量數(shù)量）；最后，輸出每棵決策樹的回歸結(jié)果，取均值得到最終結(jié)果。隨機(jī)森林模型避免了數(shù)據(jù)不平衡或單一特征變量帶來的過擬合現(xiàn)象，且降低了噪聲對預(yù)測效果的影響，決策樹的數(shù)量n和特征變量m對模型的泛化能力影響較大[13]。模型結(jié)構(gòu)見圖5，數(shù)據(jù)回歸公式如下：

圖5 隨機(jī)森林的模型結(jié)構(gòu)

式中：為回歸平均估計，Xn為隨機(jī)抽取的樣本集，E為與Xn有關(guān)的期望，Θ為因變量。

以均方根誤差（SRMSE）作為隨機(jī)森林的誤差估計值對n和m的數(shù)量進(jìn)行調(diào)整，見圖6。圖6（a）中固定n=50，在m=3 時，訓(xùn)練樣本的SRMSE最小為0.045 1 m/s；圖6（b）中固定m=3，在n=150 時，訓(xùn)練樣本的SRMSE最小為0.036 2 m/s。綜上，確定在n=150、m=3的訓(xùn)練效果最好。

圖6 超參數(shù)與SRMSE的關(guān)系

將數(shù)據(jù)代入訓(xùn)練好的隨機(jī)森林模型，擬合結(jié)果和預(yù)測誤差見圖7。模型在訓(xùn)練集和預(yù)測集上的擬合程度較好，預(yù)測集的擬合優(yōu)度（R2）并沒有下降太多，說明模型具有較強(qiáng)的泛化能力和魯棒性；預(yù)測結(jié)果的最大相對誤差為7.87%，平均相對誤差為2.08%，誤差范圍在氣液混輸管道工程實(shí)踐的要求內(nèi)，說明預(yù)測模型可以較好反映不同因素與臨界攜液流速之間的非線性關(guān)系。

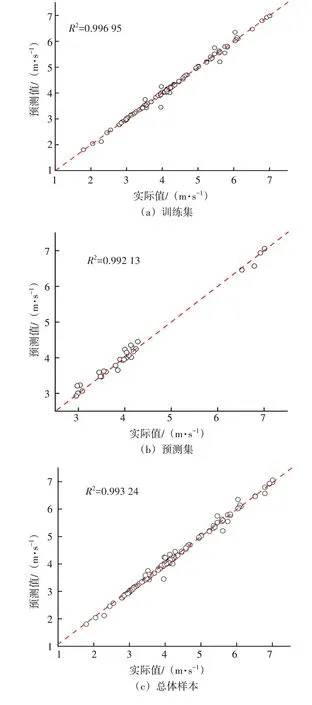
圖7 擬合結(jié)果與預(yù)測誤差

5 現(xiàn)場驗(yàn)證

將本文模型與陳建磊模型[4]、王旭模型[7]進(jìn)行對比，考慮到現(xiàn)場實(shí)際管道高程不可能只具有單一的上坡段或下坡段，而是具有多起伏特性，故取不同上傾段臨界攜液流速的最大值作為模型值。同時，在現(xiàn)場通過控制井口氣嘴壓力，調(diào)節(jié)氣體流量，將井口壓力最小值對應(yīng)的氣速定義為臨界攜液流速的實(shí)際值（在此集輸管道的出口壓力固定）。取20口氣井進(jìn)行對比，結(jié)果見圖8。

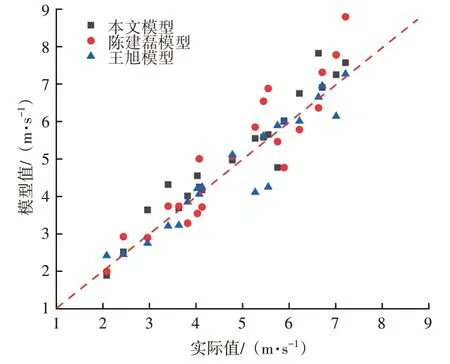
圖8 不同模型的結(jié)果對比

如模型值大于實(shí)際值，則計算得到的臨界攜液流速可以指導(dǎo)現(xiàn)場實(shí)際，用模型值調(diào)整流速可以避免管道積液；反之，現(xiàn)場集輸管道存在積液的可能性較大。本文模型有2 口氣井出現(xiàn)了誤判，模型符合率為90%；陳建磊模型、王旭模型分別有9 口、7 口氣井出現(xiàn)了誤判，模型符合率分別為55%、65%，這也再次證明了本文模型的科學(xué)性和適用性。

6 結(jié)論

1）通過最小壓降梯度模型確定臨界攜液流速，壓力與臨界攜液流速呈冪函數(shù)關(guān)系，溫度、管徑與臨界攜液流速呈線性正相關(guān)，含水率、上傾角與臨界攜液流速呈對數(shù)關(guān)系。

2）通過對均勻?qū)嶒?yàn)設(shè)計中的偏回歸系數(shù)檢驗(yàn)，單因素中上傾角對臨界攜液流速的影響最大，其次為含水率和系統(tǒng)壓力；二次項(xiàng)因素中，系統(tǒng)壓力和上傾角的交互作用最強(qiáng)。

3）通過優(yōu)選決策樹和特征變量建立隨機(jī)森林模型，預(yù)測臨界攜液流速的最大相對誤差為7.87%，平均相對誤差為2.08%，現(xiàn)場驗(yàn)證結(jié)果的模型符合率為90%，證明該模型具有較強(qiáng)的適用性，可以用于指導(dǎo)現(xiàn)場生產(chǎn)。