基于免疫粒子群的水輪機調(diào)節(jié)系統(tǒng)動態(tài)滑模控制系統(tǒng)

張繼光，丁正紅，李騰飛

（陜西省水電開發(fā)集團股份有限公司，西安 710065）

開發(fā)水力發(fā)電對于能源安全、水資源利用、環(huán)境保護等方面有著重要的意義[1]。水電站發(fā)電可通過改變水輪機速度達到對輸出功率的調(diào)整。傳統(tǒng)的控制器已經(jīng)滿足不了水輪機的非線性和負載的無規(guī)律變化，因此為了提高水輪機的控制效果，近年來，許多學(xué)者做了不少研究。如文獻[2]通過對PI 控制器采用模糊處理，提出了一種參數(shù)可以隨著水輪機轉(zhuǎn)速實時變化的滑模控制系統(tǒng)，雖然可以控制水輪機調(diào)節(jié)系統(tǒng)的抖振問題，但是模糊控制的設(shè)計需要大量的經(jīng)驗，而且控制精度低；文獻[3]提出一種自適應(yīng)趨近率的滑模變結(jié)構(gòu)控制系統(tǒng)，該系統(tǒng)適用于非線性系統(tǒng)，可以屏蔽干擾，修正目標(biāo)軌道的跟蹤控制，從而達到控制需求。但是該系統(tǒng)存在參數(shù)配置不好，收斂速度慢的問題。

免疫粒子群算法具有魯棒性，適用復(fù)雜多變的求解問題，具有收斂速度快、全局尋優(yōu)能力強的特點。為此本文結(jié)合免疫粒子群算法以及動態(tài)滑膜控制，提出一種基于免疫粒子群的水輪機調(diào)節(jié)系統(tǒng)動態(tài)滑模控制系統(tǒng)，保障水輪機調(diào)節(jié)系統(tǒng)的靈活調(diào)度和安全穩(wěn)定運行，最大程度保障水力發(fā)電效果，促進清潔能源可持續(xù)發(fā)展。

1 水輪機調(diào)節(jié)系統(tǒng)動態(tài)滑模控制系統(tǒng)

1.1 水輪機調(diào)節(jié)系統(tǒng)動態(tài)滑模控制系統(tǒng)結(jié)構(gòu)

水輪機調(diào)節(jié)系統(tǒng)動態(tài)滑模控制系統(tǒng)的框架圖如圖1 所示。

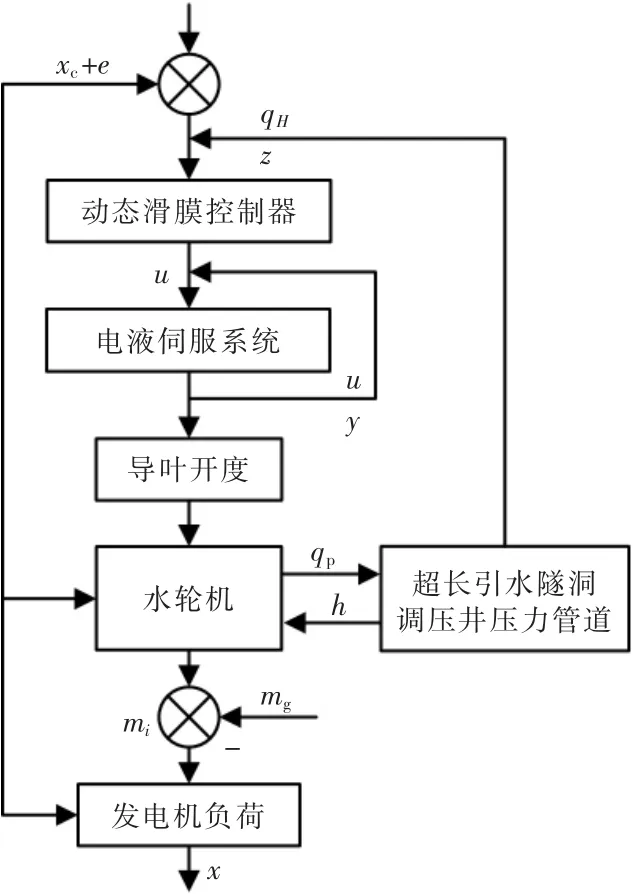
圖1 水輪機調(diào)節(jié)系統(tǒng)動態(tài)滑膜控制系統(tǒng)框架圖Fig.1 Frame diagram of dynamic sliding film control system of hydraulic turbine governing system

該隧洞的動力學(xué)方程具有非線性，表達式為

式中：超長隧洞的水流慣性時間常數(shù)用TwH0描述；調(diào)壓室水位的變化幅度用z 來描述；水輪機的水頭損失用hH0描述；水頭用H0來表示；超長引水隧洞的流量用qH來描述。

調(diào)壓室的動力學(xué)方程表達式為

式中：壓力管道流量用qp表示；調(diào)壓室時間常數(shù)用TF表示。

水輪機力矩、流量的表達式為

式中：水輪機力矩的傳遞系數(shù)分別用eh、ex和ey表示；水輪機流量的傳遞系數(shù)分別用eqh、eqx和eqy表示；力矩偏差的相對值為mt；發(fā)電機轉(zhuǎn)速偏差的相對值為x；導(dǎo)葉開度的偏差相對值為y。

電液伺服機構(gòu)作為水輪機的主要驅(qū)動裝置，可以放大控制信號并驅(qū)動導(dǎo)葉機構(gòu)的運動。電液伺服機構(gòu)的動力學(xué)方程表達式為

式中：電液伺服機構(gòu)的時間常數(shù)用Ty描述；控制器輸出用u 來描述。

綜上所述，建立水輪機調(diào)節(jié)系統(tǒng)方程組表示為

水輪機調(diào)節(jié)系統(tǒng)的方程組轉(zhuǎn)換為標(biāo)準(zhǔn)形式來方便控制器的建立。n 階非線性動力系統(tǒng)的表達式為

式中：水輪機調(diào)節(jié)系統(tǒng)的狀態(tài)向量為X；n 維向量場為A（X）和B；有限控制輸出為u；輸出向量為Y。

通過式（6）能夠找到理想軌跡的控制律xd，達到動態(tài)滑膜控制下的水輪機調(diào)節(jié)系統(tǒng)按照理想軌跡進行輸出，目的是為了讓跟蹤誤差xd-x 無限趨近于0。

1.2 電液伺服系統(tǒng)

電液伺服系統(tǒng)通過液壓傳動原理創(chuàng)建的自動控制系統(tǒng)[4-5]。電液伺服系統(tǒng)具備輸出功率大、控制精度高等優(yōu)點，在工業(yè)生產(chǎn)的各個領(lǐng)域中廣泛應(yīng)用，可通過控制油缸位置，保障對水輪機狀態(tài)穩(wěn)定和精確調(diào)節(jié)，并及時跟蹤和響應(yīng)系統(tǒng)狀態(tài)的變化。其中位移傳感器用于采集實際位置信號，轉(zhuǎn)換成電壓電流信號后，反饋至動態(tài)滑膜控制器，形成閉環(huán)結(jié)構(gòu)。電液伺服系統(tǒng)結(jié)構(gòu)如圖2 所示。

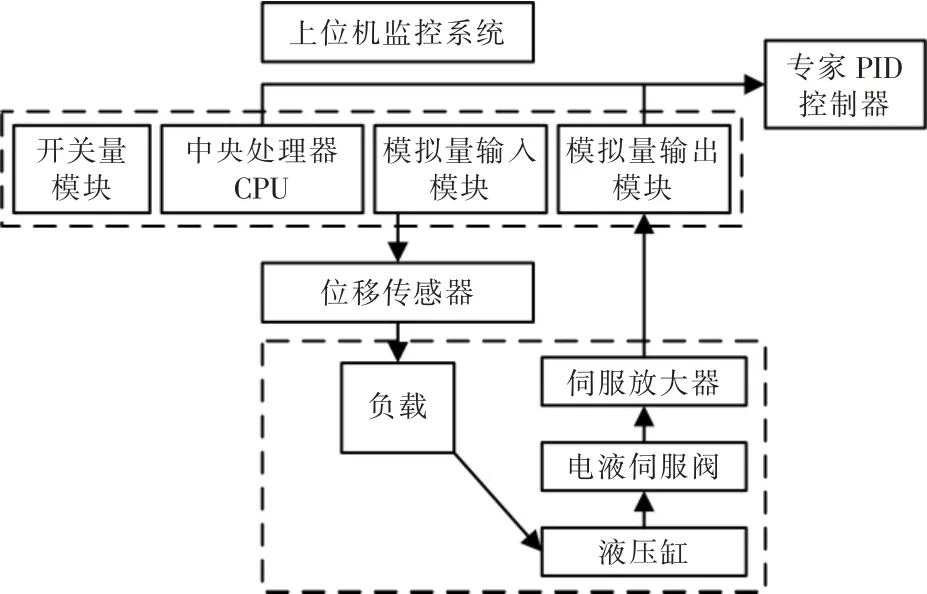
圖2 電液伺服系統(tǒng)框架圖Fig.2 Frame diagram of electro-hydraulic servo system

1.3 動態(tài)滑模控制器

在1.1 小節(jié)構(gòu)建水輪機調(diào)節(jié)系統(tǒng)狀態(tài)方程的基礎(chǔ)上，秉持水輪機調(diào)節(jié)系統(tǒng)的動態(tài)和穩(wěn)態(tài)運行目標(biāo)，布局與調(diào)節(jié)系統(tǒng)控制變量維度一致的輸出方程，即：

式中：布局的輸出變量用w 來描述；輸出的加權(quán)矩陣表達式為C=［c1c2c3c4］；輸出的積分項系數(shù)用k 描述；調(diào)速器永態(tài)轉(zhuǎn)差率用bp描述。

對控制系統(tǒng)動態(tài)性能的要求用Cx 表示，設(shè)Cj（j=1，2，3，4）分別對應(yīng)不同工況運行下的取值，系統(tǒng)運行過程中，水壓波動幅度小，與水壓相關(guān)的系數(shù)c3、c4通常取0；轉(zhuǎn)速加權(quán)系數(shù)用c1來描述，開度加權(quán)系數(shù)用c2來描述；進行構(gòu)建的輸出值全面考慮了水輪機調(diào)節(jié)過程中動態(tài)和靜態(tài)的要求。系統(tǒng)的動態(tài)輸出方程為

式中：動態(tài)滑模控制系統(tǒng)的不確定參數(shù)函數(shù)為f（x，θ）=CF（x，θ）+k（x1+bpx2）；輸入系數(shù)為b=-CB∈R，b≠0的前提條件是當(dāng)c2≠0。

滑模控制是采用控制輸入的增加來解決系統(tǒng)不確定動態(tài)特征的方法[6]。為此，需要對不確定動態(tài)特性具有已知上界的要求。假設(shè)存在已知的且滿足條件的正定上界函數(shù)ρ（·），即：

通過采用具有滑模結(jié)構(gòu)的魯棒控制方案，可以有效處理系統(tǒng)中的未知動態(tài)特性，并獲得期望的控制性能。

根據(jù)水輪機調(diào)節(jié)系統(tǒng)在不同運行工況下的性能要求，可以設(shè)計一個參考模型。對于式（9）所描述的不確定參數(shù)系統(tǒng)，其控制目標(biāo)是使系統(tǒng)的輸出w（t）跟蹤參考模型的輸出wd∈R。方便后續(xù)設(shè)計的跟蹤誤差定義為

基于根據(jù)誤差結(jié)果，建立動態(tài)方程，整理得到：

基于上述系統(tǒng)的動態(tài)方程，得到滑模控制器的輸出控制項表達式為

可通過控制項u 保障系統(tǒng)的輸出w（t）跟蹤參考模型的輸出wd∈R。式中，正反饋增益用ke∈R+表示，定義符號函數(shù)sgn（e）為

1.4 基于免疫粒子群算法的動態(tài)滑模控制器參數(shù)優(yōu)化

為進一步提升滑模控制器對水輪機調(diào)節(jié)系統(tǒng)控制效果，采用免疫粒子群優(yōu)化算法對系統(tǒng)滑模控制器的輸出控制項u 進行優(yōu)化[7]。通過優(yōu)化滑膜控制器的運行參數(shù)，提高系統(tǒng)整體性能。結(jié)合免疫種群和粒子群優(yōu)化算法的方式，達到對動態(tài)滑模控制系統(tǒng)最佳參數(shù)尋找的目的[8-9]。免疫粒子群算法是將粒子群個體描述為滑模控制器的輸出控制項u 的可行解，將尋找最優(yōu)控制參數(shù)的過程模仿成粒子個體搜查的過程，是一種全局搜索的優(yōu)化算法。設(shè)置Q為免疫種群，g 為供水系統(tǒng)的關(guān)系因子。免疫粒子群對滑模控制器的輸出控制項進行優(yōu)化的適應(yīng)度計算公式如下：

通過對其賦值得到每個控制輸入值的適應(yīng)度，即：

式中：代表各免疫粒子的適應(yīng)度概率用Pi（qi）描述；δ 代表免疫記憶細胞；qi表示迭代次數(shù)；N 代表粒子群規(guī)模；控制參數(shù)的適應(yīng)度和需求類型的選擇概率用Px描述，則有：

式中：控制參數(shù)u 的適應(yīng)度用f（qi）描述。

依據(jù)式（16）獲取適應(yīng)度最小的免疫粒子作為滑模控制器的輸出控制項u 的最優(yōu)解，完成水輪機調(diào)節(jié)系統(tǒng)的最佳控制。

2 實驗結(jié)果與分析

使用Octave 軟件搭建仿真實驗，深入研究本文設(shè)計水輪機調(diào)節(jié)系統(tǒng)動態(tài)滑膜控制系統(tǒng)的應(yīng)用情況，水輪機調(diào)節(jié)系統(tǒng)的實驗參數(shù)設(shè)置如表1 所示。

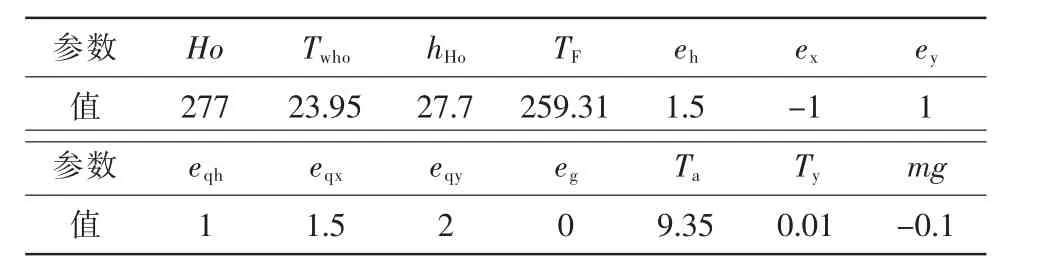
表1 水輪機調(diào)節(jié)系統(tǒng)參數(shù)Tab.1 Parameters of hydraulic turbine governing system

為驗證研究的水輪機調(diào)節(jié)系統(tǒng)動態(tài)滑模控制系統(tǒng)的有效性和適配性，選擇鋸齒波信號和階躍信號作為系統(tǒng)的輸入，設(shè)定動態(tài)滑模控制器的跟蹤軌跡，并通過與傳統(tǒng)滑模控制器對比檢驗本文系統(tǒng)的有效性。兩種控制器的鋸齒波、階躍信號參數(shù)如表2和表3 所示。

表2 動態(tài)滑模控制器參數(shù)Tab.2 Parameters of dynamic sliding mode controller

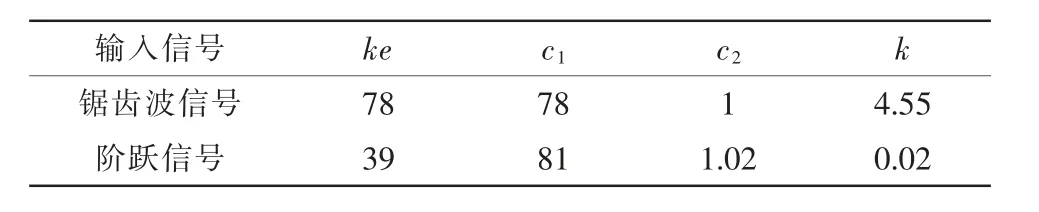
表3 傳統(tǒng)滑模控制器參數(shù)Tab.3 Parameters of traditional sliding mode controller

對水輪機調(diào)節(jié)系統(tǒng)的追蹤路線如圖3 所示。由圖3 可知，傳統(tǒng)的滑模控制器在兩種信號下的跟蹤軌跡有偏差，而設(shè)計的動態(tài)滑模控制器能夠保證水輪機調(diào)速裝置在選定的軌道上平穩(wěn)工作，同時在速度軌道跟蹤上動態(tài)反饋效果良好，并且不管是階躍還是鋸齒波，所設(shè)計的動態(tài)滑模控制器均具備魯棒性和強跟蹤能力。

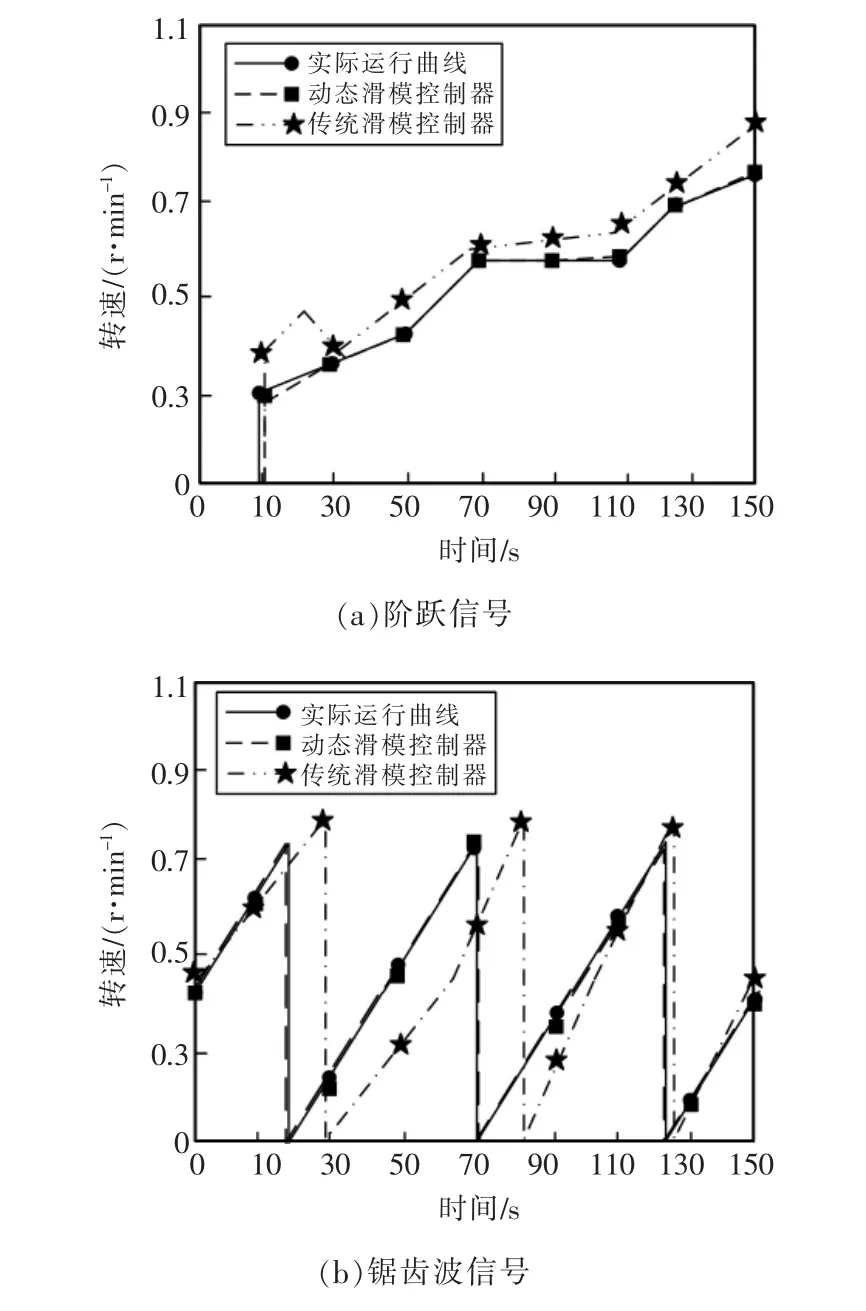
圖3 不同信號下動態(tài)滑模控制的軌跡跟蹤曲線Fig.3 Trajectory tracking curves of dynamic sliding mode control under different signals

為了分析比較研究所設(shè)計控制系統(tǒng)的動態(tài)滑模控制器和傳統(tǒng)滑模控制器對水輪機調(diào)節(jié)系統(tǒng)的控制性能，利用兩種控制器將水輪機穩(wěn)定在隨機的固定點，并采用兩種控制器來調(diào)整系統(tǒng)的響應(yīng)。在兩種信號下的轉(zhuǎn)速誤差情況如圖4 所示。由圖4（a）可知，在階躍信號下，兩種控制器的轉(zhuǎn)速在快穩(wěn)定之前，傳統(tǒng)滑模控制器抖振很嚴(yán)重，而且轉(zhuǎn)速誤差變化明顯。而研究的動態(tài)滑模控制器沒有出現(xiàn)明顯的抖振現(xiàn)象，轉(zhuǎn)速誤差幾乎為0，因此對水輪機調(diào)節(jié)系統(tǒng)的控制性起到了穩(wěn)定的作用。由圖4（b）可知，在鋸齒波信號下，兩種控制器的轉(zhuǎn)速在穩(wěn)定之后，傳統(tǒng)滑模控制器依然有連續(xù)的抖振現(xiàn)象，而研究的動態(tài)滑模控制器依然平穩(wěn)，而且誤差幾乎為0。因此對動態(tài)滑模控制器的應(yīng)用可以控制水輪機調(diào)節(jié)系統(tǒng)穩(wěn)定運行，具有良好的動態(tài)響應(yīng)。

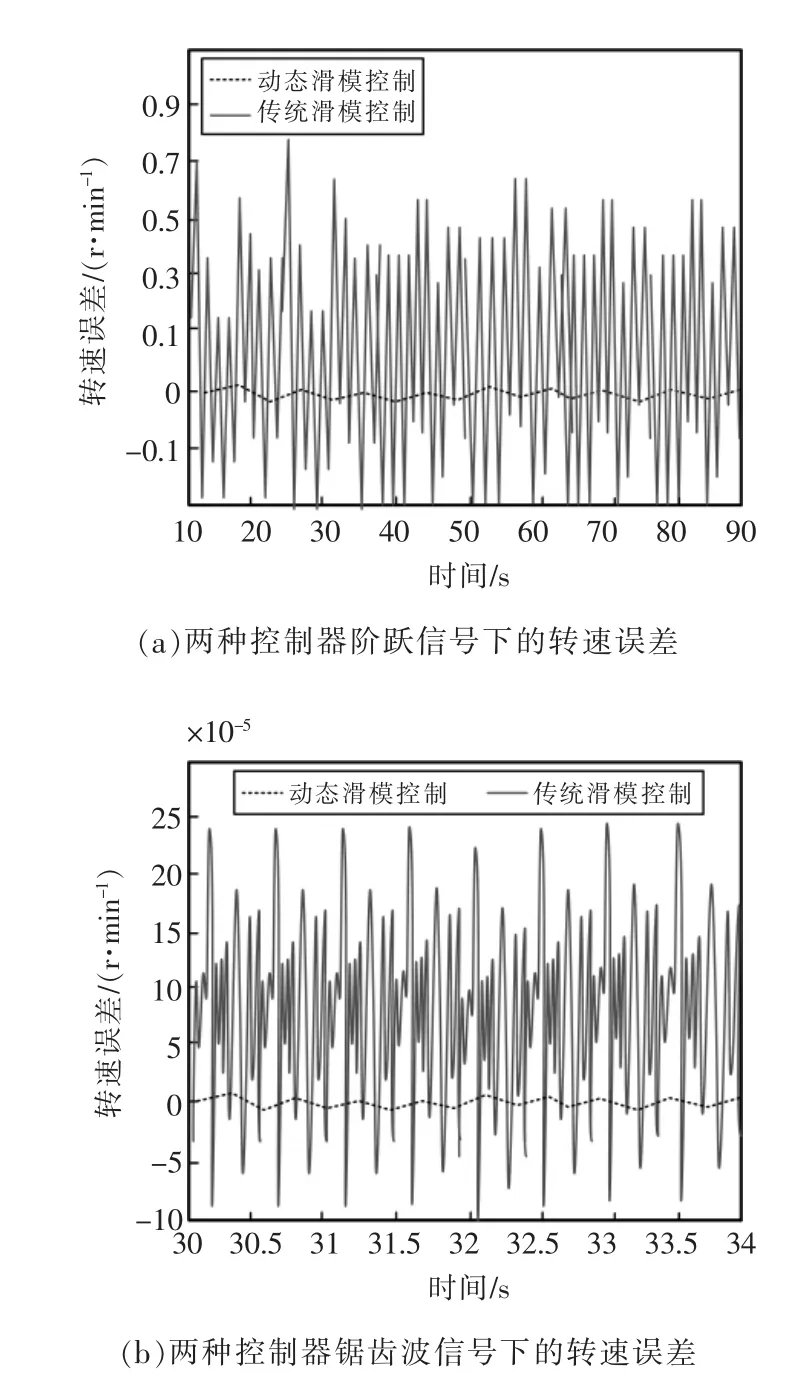
圖4 控制器在不同參考信號下的轉(zhuǎn)速誤差Fig.4 Speed error of controller under different reference signals

為了驗證免疫粒子群（IPSO）的性能，選取遺傳算法（GA）和混沌算法（CA）對水輪機調(diào)節(jié)系統(tǒng)動態(tài)滑模控制器進行參數(shù)優(yōu)化結(jié)果為對比。3 種算法的種群規(guī)模和最大迭代次數(shù)都相同。為了排除算法的隨機性，對3 種算法分別獨立運行100 次，統(tǒng)計結(jié)果得到最優(yōu)控制參數(shù)如表4 所示。由表4 可知，經(jīng)IPSO 算法得到的最優(yōu)值、平均值和標(biāo)準(zhǔn)差相較于GA 和CA 算法均有明顯降低，最優(yōu)適應(yīng)度值分別下降了2.12%和2.83%；平均適應(yīng)度值分別下降了3.34%和1.35%。研究選用的IPSO 的標(biāo)準(zhǔn)差僅為0.0086，明顯低于其他兩種算法。因此，基于免疫粒子群優(yōu)化的動態(tài)滑模控制器具有參數(shù)精度較高和穩(wěn)定性好的優(yōu)勢。

表4 三種算法參數(shù)優(yōu)化的統(tǒng)計結(jié)果Tab.4 Statistical results of parameter optimization of three algorithms

為了更加直觀的比較，對3 種算法進行100 次獨立計算得到最優(yōu)適應(yīng)度值，3 種算法收斂曲線如圖5 所示。由圖5 可知，GA 算法擁有較好的初始解，但是IPSO 算法的收斂速度明顯快于其他兩種算法，在13 代左右就已完成收斂，而GA 和CA 算法分別在21 和32 左右才成功收斂。實驗結(jié)果表明，研究的免疫粒子群算法對動態(tài)滑模控制器參數(shù)的尋優(yōu)能力優(yōu)于GA 和CA 算法，效率更高，能夠為水輪機調(diào)節(jié)系統(tǒng)的動態(tài)滑模控制器提供更優(yōu)的參數(shù)選取方案。

圖5 最優(yōu)適應(yīng)度值收斂曲線Fig.5 Convergence curve of optimal fitness value

3 結(jié)語

研究的基于免疫粒子群動態(tài)滑模控制系統(tǒng)，用于水輪機調(diào)節(jié)系統(tǒng)的精確跟蹤控制。對研究的控制系統(tǒng)的實際應(yīng)用效果進行相關(guān)數(shù)據(jù)分析，并確定免疫粒子群擁有計算精度高和收斂速率快的優(yōu)勢，為水輪機的控制系統(tǒng)提出更優(yōu)的參數(shù)選取；同時，對動態(tài)滑模控制系統(tǒng)的研究比一般的滑模控制器有著更好的特性，該系統(tǒng)研究了在不同條件下都能夠正確跟蹤，并能夠正確處理滑模的抖振問題，從而改善了水輪機調(diào)節(jié)系統(tǒng)的控制特性，具有高魯棒性。