不同控制策略下直驅風電機組的機網耦合特性及穩定性分析

饒儀明，呂 敬，戴金水，王 晗，蔡 旭

（電力傳輸與功率變換控制教育部重點實驗室（上海交通大學）,上海市 200240）

0 引言

直驅全功率風電機組是風力發電機的主流機型之一,尤其在海上風電中占主導地位［1］。然而,直驅風電機組與弱交流電網［2］、串補網絡［3］、柔性直流輸電系統［4-5］等交/直流電網間的動態交互易引發寬頻振蕩現象,近年來引起了工業界和學術界的廣泛關注。

直驅風電機組通過全功率背靠背變流器接入電網,包含機側變流器和網側變流器。機、網側變流器多采用傳統矢量控制策略,機側變流器通過控制永磁同步發電機的輸出功率實現最大功率跟蹤,網側變流器控制直流母線電壓恒定［6］。早期研究普遍認為,直驅風電機組的機、網側變流器通過直流母線電容解耦,其并網特性主要由網側變流器決定。因此,研究中通常忽略機側系統（包括發電機和機側變流器）動態,將機側系統簡化為一個理想功率源［7-9］。然而,文獻［10-11］定性分析了機側系統動態對直驅風電機組交流側阻抗特性的影響,指出忽略機側系統動態可能會導致并網穩定性的誤判。文獻［12］定量分析了直驅風電機組機網耦合特性及其關鍵影響因素,揭示了機側系統動態對直驅風電機組并網穩定性的影響機制。在傳統矢量控制外,文獻［13］提出了一種增強直驅風電機組電網故障穿越能力的新型雙閉環矢量控制策略,該控制策略通過機側變流器控制直流母線電壓,通過網側變流器控制有功功率。文獻［14］對比研究了直驅風電機組在該新型矢量控制策略和傳統矢量控制策略下的直流側動態及其關鍵影響因素,指出當直流母線電壓由機側變流器控制時,直流側動態的阻尼較弱,但并沒有分析兩種控制策略下直驅風電機組的機網耦合特性及并網穩定性。

近年來,隨著風電接入比例的不斷提高,具有電網主動支撐能力的構網型風電機組成為研究熱點［15］。為使并網逆變器模擬同步發電機的運行特性,文獻［16］依據同步發電機的轉子運動方程提出了虛擬同步機（virtual synchronous generator,VSG）控制策略,使并網逆變器具備功率同步特性；文獻［17］則依據并網逆變器和同步發電機在結構和特性上的對偶關系,提出了并網逆變器的慣性自同步控制（inertia synchronization control,ISynC）策略,利用直流母線電容的慣性實現同步并網。基于上述并網逆變器的兩種典型構網型控制,提出了兩種主流的構網型直驅風電機組控制策略:1）機側變流器采用矢量控制方案控制直流母線電壓,網側變流器采用VSG 控制實現功率同步并網［18］,即VSG 型直驅風電機組；2）機側變流器采用矢量控制方案控制有功功率或其相關量（如電磁轉矩）實現最大功率跟蹤,網側變流器采用直流電容慣性同步控制實現慣性同步并網［19］,即ISynC 型直驅風電機組。在構網型直驅風電機組的小信號穩定性分析方面,文獻［20］利用阻抗法研究了VSG 型直驅風電機組并弱電網的穩定性,指出VSG 型直驅風電機組交流側阻抗在基頻以下的容性特性可能導致其接入感性弱電網時產生失穩風險；文獻［21］采用特征值分析法研究了VSG 型直驅風電機組的并網穩定性,指出VSG 型直驅風電機組具有較好的弱電網適應性,但在強電網下容易出現低頻振蕩問題；文獻［19］分析了ISynC 型直驅風電機組接入弱電網的穩定性,指出附加慣量傳遞控制環節會降低ISynC 型直驅風電機組弱電網運行穩定性。然而,上述文獻沒有討論構網型直驅風電機組的機網耦合特性,對不同構網型控制策略下機側系統動態對直驅風電機組并網特性的影響尚不明確。

綜上所述,現有研究僅對傳統矢量控制策略下直驅風電機組的機網耦合特性進行了深入分析,但對其他典型控制策略下直驅風電機組的機網耦合特性及其關鍵影響因素尚不明確。此外,現有文獻尚缺乏針對不同控制策略下直驅風電機組統一形式的寬頻阻抗建模方法,尤其是尚無文獻建立ISynC 型直驅風電機組的阻抗模型。為此,本文針對直驅風電機組機網耦合特性開展深入研究,建立4 種典型控制策略下直驅風電機組統一形式的交流側寬頻阻抗模型,并進行掃頻驗證；基于解析阻抗模型和機網耦合度指標對不同控制策略下直驅風電機組的機網耦合特性及其關鍵影響因素進行對比分析；以直驅風電機組并弱交流電網為分析案例,驗證不同控制策略下機網耦合特性對直驅風電機組并網穩定性分析的影響。

1 不同控制策略下直驅風電機組的阻抗模型

1.1 直驅風電機組的主電路及控制結構

圖1 為直驅風電機組的主電路結構及4 種典型控制策略的控制框圖。圖中:s為拉普拉斯算子；PLL 表示鎖相環；MPPT 表示最大功率點跟蹤；SVPWM 表示空間矢量脈寬調制；PMSG 表示永磁同步發電機；Vmabc和Imabc分別為機側變流器交流側三相電壓和電流；Cdc為直流母線電容；Vdc為直流母線電壓；Vabc和Iabc分別為網側變流器交流側三相電壓和電流；Viabc為經過電感濾波器后的三相交流電壓；Lf和Rf分別為電感濾波器的等效電感和電阻；ωm為永磁同步發電機的轉速；θm和θe分別為轉子的機械角度和電角度；np為永磁同步發電機的極對數；Imd和Imq分別為Imabc經過Park 變換得到的機側變流器交流側電流的d、q軸分量；Vmd,ref和Vmq,ref分別為機側變流器控制器輸出的電壓調制信號d、q軸分量；Vmabc,ref為Vmd,ref和Vmq,ref經過反Park 變換得到的機側變流器三相電壓調制信號；dmabc為機側變流器的開關信號；P和Q分別為直驅風電機組輸出的有功功率和無功功率；θ為網側變流器控制器Park 變換所使用的同步旋轉角度；Id和Iq分別為Iabc經過Park 變換得到的網側變流器交流側電流的d、q軸分量；Vid和Viq分別為Viabc經過Park 變換得到的d、q軸分量；Vd,ref和Vq,ref分別為網側變流器控制器輸出的電壓調制信號d、q軸分量；Vabc,ref為Vd,ref和Vq,ref經過反Park 變換得到的網側變流器三相電壓調制信號；dabc為網側變流器的開關信號；Te為永磁同步發電機的電磁轉矩,Te,ref為其給定值；Imd,ref和Imq,ref分別為機側變流器交流側電流參考值的d、q軸分量；ωe和Lm分別為永磁同步發電機的轉子電角速度和繞組電感；ψr為磁鏈；ω0為基頻對應的角頻率；Id,ref和Iq,ref分別為網側變流器交流側電流參考值的d、q軸分量；Vdc,ref和Qref分別為直流電壓和無功功率的給定值；HT(s)、Hmc（s）、Hdc(s)、HQ（s）、Hc（s）分別為電磁轉矩控制器、機側電流控制器、直流電壓控制器、無功功率控制器和網側電流控制器的傳遞函數；HPQ（s）為網側變流器功率外環控制器的傳遞函數；Pref為有功功率的給定值；J為虛擬慣量；K為無功控制系數；Dp為頻率下垂系數；Dq為電壓下垂系數；Vt,ref為反電動勢電壓幅值的給定值；Vd為Vabc經過Park 變換得到的d軸分量；ω為有功控制環生成的同步角速度；Vdc,Base為直流電壓基準值；ωBase為網側變流器輸出電壓角頻率的基準值；Vd,Base為網側變流器交流側d軸電壓的基準值；Vt,Base為反電動勢電壓幅值的基準值；SBase為直驅風電機組的額定容量。

圖1 直驅風電機組主電路及4 種控制策略結構示意圖Fig.1 Schematic diagram of main circuit and four types of control strategies of direct-drive wind turbines

直驅風電機組的主電路結構及應用最為廣泛的雙閉環矢量控制策略——控制策略1（CS1）在文獻［12］中得到了詳細闡述,不再贅述。

對直驅風電機組的另外3 種典型控制策略描述如下:

控制策略2（CS2）［13］:機側和網側變流器均采用雙閉環矢量控制,但與CS1 不同的是,CS2 機側變流器控制直流母線電壓,網側變流器控制有功功率。

控制策略3（CS3）［18］:機側變流器控制直流母線電壓,其控制結構與CS2 的機側控制完全一致,但網側變流器采用VSG 控制。VSG 控制無需PLL,而是利用有功控制環和無功控制環分別生成同步旋轉角度θ和d軸調制電壓Vd,ref。

控 制 策 略4（CS4）［19］:機 側 變 流 器 控 制 有 功 功率,其控制結構與CS1 的機側控制完全一致,但網側變流器采用ISynC 控制。在ISynC 控制中,直流電壓標幺值被用作網側變流器輸出電壓角頻率的標幺值,進而經過積分器生成同步旋轉角度θ。直驅風電機組輸出的無功功率Q可通過調整調制電壓的幅值來調節。此外,ISynC 控制還采用了包含高通濾波器（Tdc為高通濾波時間常數）和致穩控制系數KPSS的附加穩定控制回路來增加系統阻尼。

當調制方式為補償調制時,直驅風電機組機/網側系統解耦,采用直接調制是探討直驅風電機組機網耦合特性的前提條件［12］。因此,本文工作建立在變流器采用直接調制的基礎上。

1.2 直驅風電機組的通用小信號阻抗建模方法

基于直驅風電機組的模塊化多端口小信號模型,可以推導得到直驅風電機組交流端口阻抗的通用求解表達式,從而將不同控制策略下直驅風電機組的阻抗模型納入統一架構。

直驅風電機組的模塊化多端口小信號模型在文獻［12］中已有詳細闡述,此處不再贅述。基于直驅風電機組的模塊化多端口小信號模型,可以推導得到直驅風電機組機側系統等效至直流端口的小信號導納YdcMSS,進而推導得到直驅風電機組整體交流端口dq阻抗Zac,即

式中:“Δ”表示相應變量的小信號分量；上標“s”表示電氣系統坐標系中相應變量；Imdc為機側變流器直流側電流,以流入機側變流器為正；ZPMSG為永磁同步發電機的小信號dq阻抗矩陣；Ymdq為機側變流器的交流側自導納矩陣,主要由機側變流器的控制系統決定；Ya和Yb為機側變流器的交直流側耦合導納矩陣；Ymdc為機側變流器的直流側自導納；Ydq為網側變流器的交流側自導納矩陣,主要由網側變流器的控制系統決定；Yc和Yd為網側變流器的交直流側耦合導納矩陣,Ydc為網側變流器的直流側自導納。

值得注意的是,當推 導得到Ymdq、Ya、Ydq和Yc的詳細表達式后,可分別根據機、網側變流器的交直流側功率守恒推導得到Yb、Ymdc、Yd和Ydc的詳細表達式,具體計算方法見文獻［12］。

根據式（1）和式（2）,直驅風電機組的交流側小信號阻抗模型可通過推導關鍵參數矩陣Ymdq、Ya、Ydq、Yc的詳細表達式來建立。在直驅風電機組的阻抗模型中,控制策略的不同體現為關鍵參數矩陣的詳細表達式不同。為區分不同控制策略下的關鍵參數矩陣,本文為相應矩陣名稱附加控制策略編號,例如Ya2表示CS2 的Ya。

值得說明的是,在機側變流器控制直流母線電壓時（如CS2 和CS3）,忽略機側系統動態的直驅風電機組交流側阻抗即為網側變流器的交流側自阻抗,即有Zac,sim=(Ydq)-1。對于通過機側變流器控制實現MPPT 的CS1 和CS4,忽略機側系統動態即意味著將機側系統簡化為恒功率源。因此,CS1 或CS4 控制下忽略機側系統動態的直驅風電機組交流側阻抗可由式（2）改寫得到,即

式中:Vdc0為直流母線電壓的穩態值。

上文所得阻抗為dq阻抗模型,可根據文獻［22］將所建立的dq阻抗模型進一步轉化為單輸入-單輸出正序阻抗模型。

下文在闡述不同控制策略下直驅風電機組的阻抗模型時,僅展示關鍵參數矩陣具體表達式的關鍵推導過程。

1.3 4 種控制策略下直驅風電機組的小信號阻抗模型

由于采用CS1 的直驅風電機組的小信號阻抗模型在文獻［12］中已得到詳細闡述,本文在附錄A式（A1）中直接給出了CS1 下關鍵參數矩陣的詳細表達式。下文分別介紹CS2、CS3 和CS4 下關鍵參數矩陣的推導過程。

由于變流器控制中的解耦項對直驅風電機組正序阻抗的影響較小［23］,本文在阻抗建模過程中省略了解耦項。

1）CS2

CS2 的控制結構與CS1 類似,僅在外環控制量上存在差別。因此,CS2 下的關鍵參數矩陣推導過程與CS1 一致。由于篇幅限制,本文僅給出CS2 下機側變流器和網側變流器的外環控制方程（式（4）和式（5））以及關鍵參數矩陣的詳細表達式（式（6））。

式中:I為單位矩陣；參數矩陣A2、B2的詳細表達式見附錄A 式（A2）。

2）CS3

由于CS3 的機側變流器控制結構與CS2 完全一致,有:

VSG 控制下網側變流器的有功控制環、無功控制環的控制方程可分別表示為:

將式（8）進行小信號線性化,并考慮直接調制過程和控制系統坐標系與電氣系統坐標系之間的轉換關系,可以推導得到:

式中:參數矩陣F3、G3的詳細表達式見附錄A式（A3）。

3）CS4

由于CS4 的機側變流器控制結構與CS1 完全一致,有:

ISynC 控制下網側變流器的控制方程為:

將式（11）進行小信號線性化,并考慮直接調制過程和控制系統坐標系與電氣系統坐標系之間的轉換關系,可以推導得到:

式中:Zdqf為交流濾波器的小信號dq阻抗矩陣；參數矩 陣Ts和Tv的 詳 細 表 達 式 見 附 錄A 式（A3）,A4、B4、C4的詳細表達式見式（A4）。

1.4 阻抗模型驗證

為驗證所建立阻抗模型的準確性,在MATLAB/Simulink 中分別搭建采用上述4 種控制策略的直驅風電機組時域仿真模型,主要參數見附錄B 表B1。其中,主電路參數來源于實際工程中的直驅風電機組,4 種控制策略的控制參數則是根據文獻［19,24-25］中的控制參數整定方法設計得到。

對于每一種控制策略下的直驅風電機組仿真模型,在交流側依次注入頻率在1～1 000 Hz 范圍內的擾動電壓信號（1～200 Hz 的頻率間隔為1 Hz,201～1 001 Hz 的頻率間隔為25 Hz）,測量對應頻率下的擾動電流響應,進而可計算得到直驅風電機組在對應頻率下的交流側小信號阻抗［26］。直驅風電機組交流側小信號阻抗掃頻測量的具體步驟如附錄B 圖B1 所示。

通過上述方法可獲得4 種控制策略下直驅風電機組的寬頻阻抗（掃頻測量阻抗,即阻抗的真實值）,基于所建立的阻抗模型可以計算得到4 種控制策略下直驅風電機組的理論計算阻抗,將掃頻測量阻抗與理論計算阻抗進行對比,結果如圖2 所示。可以看到,直驅風電機組在4 種控制策略下的理論計算阻抗與掃頻測量阻抗具有很好的一致性,驗證了所建立寬頻阻抗模型的準確性。

圖2 不同控制策略下直驅風電機組阻抗模型驗證Fig.2 Impedance model validation of direct-drive wind turbines with different control strategies

2 不同控制策略下直驅風電機組機網耦合特性分析

2.1 機側系統動態總體影響的對比分析

圖3 展示了不同控制策略下是否考慮機側系統動態對直驅風電機組交流側阻抗特性的影響。4 種控制策略下的直驅風電機組主電路參數完全一致。控制參數選取方法如下:對于4 種控制策略中的雙閉環矢量控制,按照相同或相似控制環節（例如均是電流內環或均是電流外環）的閉環帶寬保持一致的原則來確定控制器比例-積分（PI）參數（基本計算方法見文獻［24］）。具體地,機/網側電流內環帶寬被設置為200 Hz,直流電壓/轉矩/功率外環帶寬被設置為10 Hz,PLL 帶寬被設置為30 Hz；對于VSG 控制和慣性同步型控制,采用典型的電壓源控制參數設計方法設計相應參數［19,25］。對比考慮機側系統動態的直驅風電機組詳細阻抗特性和忽略機側系統動態的簡化阻抗特性,可以反映機側系統動態的總體影響。

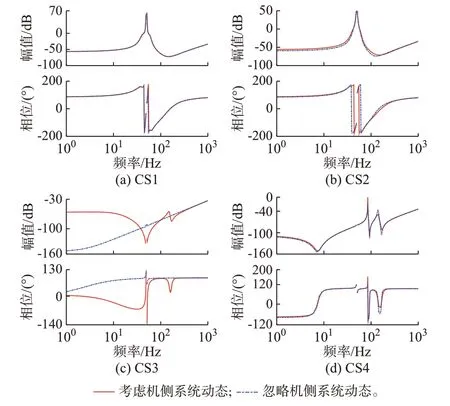
圖3 不同控制策略下直驅風電機組阻抗特性Fig.3 Impedance characteristics of direct-drive wind turbines with different control strategies

從圖3（a）可以看到,在CS1 下,紅色實線與藍色虛線幾乎完全重合,說明在CS1 下直驅風電機組的阻抗特性受其機側系統動態影響較小,即直驅風電機組機網耦合程度較低。然而,如圖3（b）所示,當直驅風電機組采用CS2 時,是否計及機側系統動態對直驅風電機組的交流側阻抗特性存在較為明顯的影響。如圖3（c）所示,在CS3 下,忽略機側系統動態的簡化阻抗特性與考慮機側系統動態的詳細阻抗特性在中低頻段（200 Hz 以下）完全不同:當忽略機側系統動態時,直驅風電機組的阻抗特性在全頻段內近似感性特性；當考慮機側系統動態時,直驅風電機組的阻抗在次同步頻段內呈現容性特性。如圖3（d）所示,采用CS4 的直驅風電機組交流側阻抗特性受機側系統動態的影響較小,與采用CS1 的直驅風電機組較為類似,說明在該控制策略下忽略機側系統動態不會對直驅風電機組的交流側阻抗模型精度產生較大影響。

因此,相較于采用CS1 或CS4,采用CS2 或CS3時直驅風電機組的機網耦合程度較高,意味著機側系統動態對直驅風電機組交流側中低頻段阻抗特性具有較大影響。

2.2 機網耦合特性的量化分析

為量化分析不同控制策略下直驅風電機組的機網耦合特性,定義機網耦合度λc,如式（13）所示。

式中:Zcom和Zsim分別為考慮和忽略機側系統動態的直驅風電機組交流側阻抗；f為頻率。

式（13）的物理含義為忽略機側系統動態對直驅風電機組交流側阻抗模型造成的相對誤差。因此,較高的耦合度說明直驅風電機組機網耦合效應較為顯著。研究發現,電網強度的變化不影響直驅風電機組在不同控制策略下機網耦合度的相對大小規律。因此,僅展示理想電網條件下采用不同控制策略的直驅風電機組的機網耦合度,結果如圖4 所示。可以看到,在大部分頻段內采用CS2 或CS3 時直驅風電機組的機網耦合度高于CS1 或CS4。

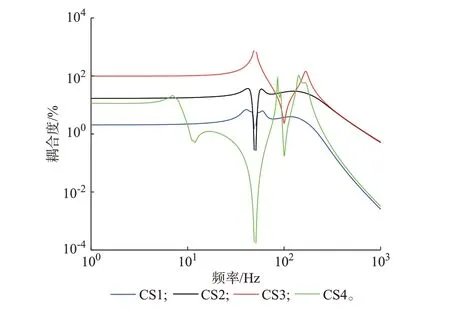
圖4 不同控制策略下直驅風電機組機網耦合度比較Fig.4 Comparison of generator-grid coupling degrees of direct-drive wind turbines with different control strategies

值得注意的是,CS2 和CS3 均是機側變流器控制直流母線電壓,而CS1 和CS4 均是網側變流器控制直流母線電壓。因此,可以得出如下結論:當機側變流器控制直流母線電壓時,直驅風電機組的機網耦合效應將會加劇,此時忽略機側系統動態會對直驅風電機組交流側阻抗模型的精度造成較大誤差。

圖4 所示為典型控制參數下不同控制策略直驅風電機組機網耦合度的比較。為說明本文研究結論具有普適性,對每一種控制方式,考慮各控制參數的不同取值,在各種參數組合下繪制直驅風電機組機網耦合度曲線,結果如附錄C 圖C1 所示。分析結果表明,即使在不同控制參數下,各控制策略的機網耦合度仍滿足上述結論,本文的研究結論具有較好的普適性。

不同控制策略下控制參數和直流母線電容對直驅風電機組機網耦合度的影響分析詳見附錄C。

3 案例研究

本章利用阻抗穩定性分析方法分析4 種控制策略下直驅風電機組并弱交流電網的穩定性。對于每一種控制策略,分別采用考慮機側系統動態的詳細阻抗模型和忽略機側系統動態的簡化阻抗模型來分析互聯系統的（潛在）振蕩頻率和穩定裕度,以驗證機網耦合特性對直驅風電機組并網系統穩定性分析的影響。圖5 展示了穩定性分析結果,其中,交流電網的短路比為3,直驅風電機組在4 種控制策略下均輸出1 MW 有功功率和0.1 Mvar 無功功率。由于交流電網等效阻抗的相位為90°,根據阻抗穩定性分析理論,當直驅風電機組與電網阻抗幅值曲線相交頻率處的直驅風電機組阻抗相位小于-90°時,互聯系統將失穩,失穩域如圖5 所示。

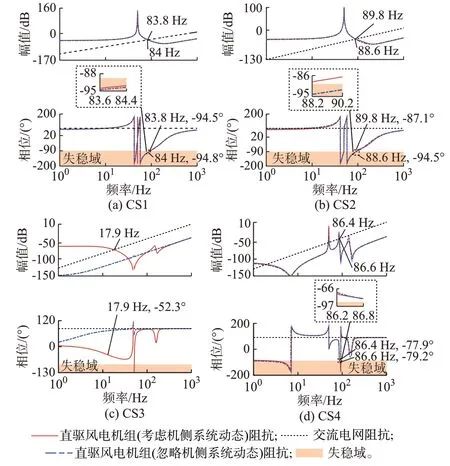
圖5 不同控制策略下直驅風電機組并網穩定性分析Fig.5 Analysis of grid-connected stability for directdrive wind turbines with different control strategies

由圖5 可以得出以下結論:

1）如圖5（a）所示,在CS1 下,無論是否考慮機側系統動態,互聯系統穩定性分析結果都落在失穩域內,且分析得到的振蕩頻率和相位裕度非常接近。具體地,當忽略機側系統動態時,分析得到的振蕩頻率和相位裕度分別為84 Hz 和-4.8°；當考慮機側系統動態時,分析得到的振蕩頻率和相位裕度分別為83.8 Hz 和-4.5°。因此,對于采用CS1 的直驅風電機組,忽略機側系統動態對其并網穩定性分析結果的影響較小。

2）如圖5（b）所示,在CS2 下,當考慮機側系統動態時,互聯系統穩定性分析結果落在失穩域外,相位裕度為2.9°,表明系統穩定；而當忽略機側系統動態時,互聯系統穩定性分析結果落在失穩域內,系統穩定裕度被誤判為-4.5°,表明系統失穩。因此,對于采用CS2 的直驅風電機組,忽略機側系統動態對其并網穩定性分析結果的準確性影響較大。

3）如圖5（c）所示,在CS3 下,考慮機側系統動態的詳細阻抗與忽略機側系統動態的簡化阻抗在中低頻段（如200 Hz 以下）存在較大差異。考慮機側系統動態的直驅風電機組詳細阻抗與交流電網阻抗的幅頻曲線在17.9 Hz 處相交,相位裕度為37.7°；忽略機側系統動態的直驅風電機組簡化阻抗與交流電網的阻抗幅頻曲線不存在任何交點,可視為相位裕度無窮大。雖然無論考慮機側系統動態與否對采用CS3 的直驅風電機組并網系統進行穩定性分析都能夠得出系統穩定的結論,但是所得到的系統穩定裕度的分析結果存在較大差別。需要說明的是,當采用CS3 的直驅風電機組接入柔性直流輸電系統時,由于柔性直流輸電系統在次同步頻段可能存在感性負電阻特性,可能與直驅風電機組在次同步頻段的容性特性相互作用,產生振蕩風險。然而,在CS3下,忽略機側系統動態的直驅風電機組阻抗在全頻段內均是感性,無法反映該場景下的振蕩風險。因此,對于采用CS3 的直驅風電機組,忽略機側系統動態對其并網穩定性分析結果的影響較大。

4）如圖5（d）所示,在CS4 下,無論考慮機側系統動態與否,互聯系統穩定性分析結果都落在失穩域外,表明系統穩定,且分析得到的振蕩頻率和相位裕度較為接近,與CS1 的情況類似。因此,對于采用CS4 的直驅風電機組,機網耦合效應對其并網穩定性分析結果的影響較小。

圖6 展示了相應的時域仿真結果,其中,交流電網的初始短路比為4,當仿真進行10 s 時,將交流電網的短路比降低至3。從圖中可以看出,當采用CS1 時,直驅風電機組在電網短路比降低至3 后發生振蕩現象,公共耦合點（point of common coupling,PCC）的電流IPCC迅速畸變,與上文忽略/考慮機側系統動態的穩定性分析結果一致；當采用CS2 時,直驅風電機組在電網短路比降低至3 后仍然能夠保持穩定,與前文考慮機側系統的穩定性分析結果一致,驗證了在CS2 下忽略機側系統動態會導致系統穩定性誤判的結論；當采用CS3 或CS4時,直驅風電機組在電網短路比降低至3 后均保持穩定,驗證了上文忽略/考慮機側系統動態的穩定性分析結果的準確性。

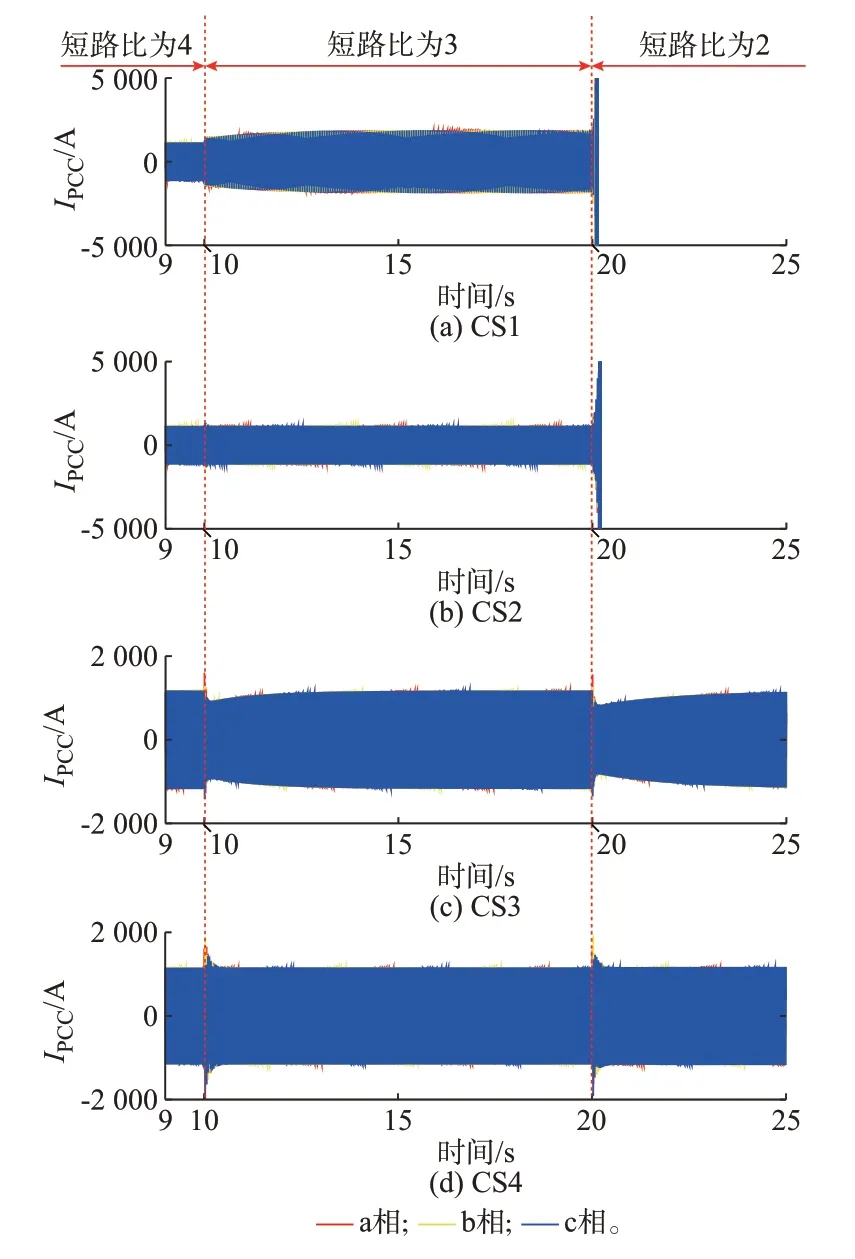
圖6 不同控制策略下直驅風電機組并網電流波形Fig.6 Grid-connected current waveforms of direct-drive wind turbines with different control strategies

另一方面,為對比不同控制策略下直驅風電機組的弱電網運行能力,在仿真第20 s 時,進一步將交流電網的短路比降低至2。對比不同控制策略下的仿真結果可以看到,當電網短路比降低至2 后,采用CS1 的直驅風電機組并網點電流由之前的等幅振蕩迅速發散,系統崩潰；采用CS2 的直驅風電機組也迅速失穩導致系統崩潰；而兩種電壓源型控制（CS3和CS4）的直驅風電機組則能在短路比為2 的極弱電網條件下繼續保持穩定運行,具有更好的弱電網運行能力。此外,對比CS1 和CS2 可知,機側變流器控制直流母線電壓的矢量控制策略可在一定程度上改善直驅風電機組的并網穩定性。

4 結語

本文建立了4 種典型控制策略下直驅風電機組的精細化寬頻阻抗模型,對比研究了不同控制策略下直驅風電機組的機網耦合特性,以及是否考慮機側系統動態對其并網穩定性分析精度的影響。結論如下:

1）當網側變流器控制直流母線電壓（如傳統矢量控制、ISynC 型直驅風電機組等）時,直驅風電機組的機網耦合程度較低,忽略機側系統動態對其并網穩定性分析精度的影響較小。

2）當機側變流器控制直流母線電壓（如VSG 型直驅風電機組等）時,直驅風電機組的機網耦合程度較高,機側系統動態對直驅風電機組交流側阻抗特性影響較大（主要體現在中低頻段）。特別地,當網側變流器采用VSG 控制時,機網耦合尤為顯著。在此類控制策略下,忽略機側系統動態可能會對直驅風電機組并網穩定性分析帶來較大誤差。

3）矢量控制策略下（如CS1 和CS2）,機側或網側變流器的控制參數以及直流母線電容值對機網耦合度具有較大影響；而電壓源控制策略下（如CS3和CS4）,機側或網側變流器控制參數對機網耦合度影響較小,且直流母線電容值主要影響中高頻段的機網耦合特性。

4）機側變流器控制直流母線電壓的矢量控制策略可在一定程度上改善直驅風電機組的并網穩定性；相較于采用電流源型控制的直驅風電機組,電壓源型控制的直驅風電機組具有更好的弱電網運行能力。

本文研究結論可為不同控制策略下直驅風電機組的建模與分析提供參考。

附錄見本刊網絡版（http：//www.aeps-info.com/aeps/ch/index.aspx），掃英文摘要后二維碼可以閱讀網絡全文。