爆破應力波對鄰近隧洞影響的有限元分析

王 丹 田安安 任喜平

(陜西引漢濟渭工程建設有限公司,陜西 西安 710010)

目前,在我國水利水電工程及其他地下工程建設中,爆破施工是隧洞掘進的常用和主要施工方法。由于爆破作業具有極大的破壞性,在隧洞爆破掘進時引起的振動會對臨近既有建筑物產生較大的影響,這也是現階段爆破施工的研究熱點和難點之一。爆破振動模型實驗具有操作過程的局限性和經濟指標的不合理性,選用數值模擬試驗分析研究爆破振動現象成為科學理論發展的必然選擇。

本文結合引漢濟渭二期工程黃池溝黑河供水連通洞出口段開挖爆破振動對臨近既有黑河引水洞圍巖穩定及襯砌結構安全性存在潛在影響的建設實際,根據隧洞爆破施工方法,通過搭建合理的三維有限元模型,選取六個爆破斷面及八個監測斷面的四個監測點,擬定相應的邊坡爆破動力荷載,對隧洞爆破開挖引起巖體振動對黑河引水洞襯砌結構的影響進行評估。

1 工程概況

引漢濟渭二期輸水工程主要由黃池溝配水工程、輸水南干線及北干線工程組成。南干線長度100.13km,始端設計流量47m3/s ,北干線長度89.54km,始端設計流量30m3/s。具體平面布置見圖1。

圖1 引漢濟渭二期輸水工程平面布置示意圖

2 計算原理

2.1 爆破機理

巖體在爆破過程中產生的破壞和炸藥耦合作用是一個動態且比較復雜的過程,其發生的時間非常短暫,往往在幾至幾十毫秒。在爆炸過程中,炸藥釋放能量的形式主要有兩種:以波的形式傳播釋放、以爆生氣體產生膨脹的作用釋放。本文選用爆炸產生應力波的作用理論[1],即設定巖體的破壞主要由巖體內部爆炸過程產生的應力波通過自由面的反射產生拉應力波導致。在數值模擬分析中,將爆破應力波作用的時間歷程和大小作為影響能量釋放的參數。

2.2 爆破荷載簡化

根據靜力平衡和圣維南原理,將等效的三角形脈沖荷載(見圖2)施加在同排炮孔的連心線與炮孔軸線所確定的平面上,不考慮炮眼的形狀[2],見圖3。

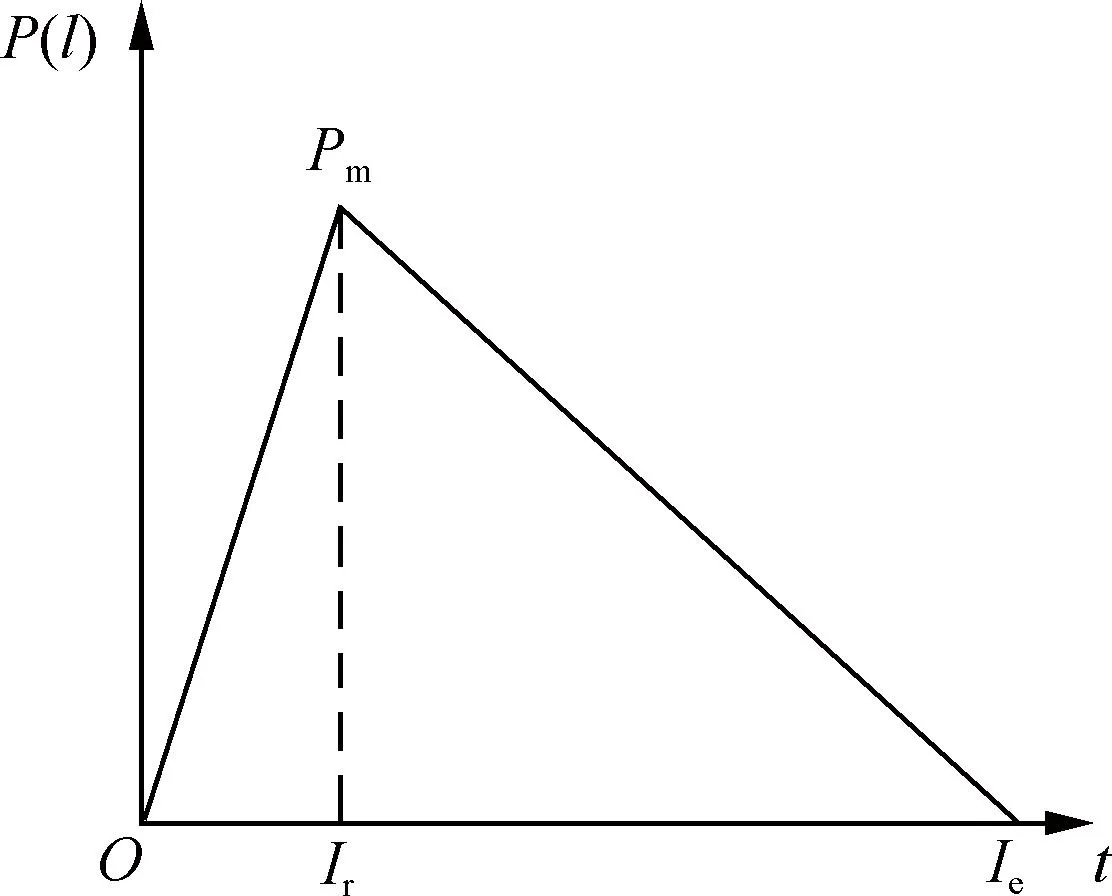
圖2 三角脈沖荷載作用時程曲線

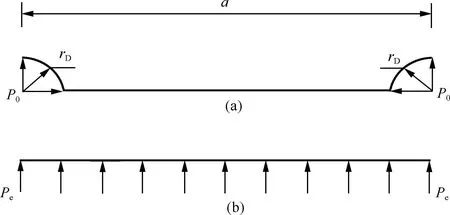
圖3 爆破荷載靜力等效示意圖

a.根據凝聚炸藥爆轟波的C-J理論計算單個炮孔的峰值荷載P0,計算公式[3-6]如下:

(1)

式中:P0為單個炮孔荷載峰值;ρe為炸藥的密度值;D為炸藥轟爆的速度值;γ為等熵指數值,一般可取3;r1為裝藥直徑;r0為炮孔半徑。

b.根據靜力等效理論計算群孔的等效爆破峰值荷載Pb,計算公式如下:

Pb=(2r0/a)P0

(2)

式中:a為炮孔間距;P0為單個炮孔荷載峰值;Pb為等效荷載峰值。

c.計算爆破荷載的加載時間和卸載時間,計算公式[7-9]如下:

(3)

(4)

式中:tr為上升段時間;ts為全段作用時間;μ為巖石泊松比;K為巖石體積壓縮模量;Q為炮孔總裝藥量;r為耦合系數。

3 模型及荷載

3.1 分析模型

為了模擬分析小凈距隧道爆破施工產生的縱向影響過程,以便分析結論具有較高的普遍性和適用性,選用MIDAS-GTS軟件構建三維有限元計算分析模型。同時,為了突出顯示重點,在模擬計算分析過程中忽略隧洞支護體系的影響,只考慮毛洞開挖過程中的爆破施工。有限元模型的尺寸長×寬×高為306m×102m×200m。隧道洞徑尺寸不變,截面選取單心圓仰拱形式,兩條隧道間的凈距選取27.6m。為盡量減少邊界效應對計算模型的影響,左、右邊界和埋深分別選取 4倍和3倍的洞徑。網格的劃分選用四節點四面體單元,模型共劃分的節點和單元分別為58185個、80638個。具體的有限元模型見圖4。

圖4 三維有限元模型

3.2 計算參數

出于最不利情況考慮,圍巖假定為Ⅳ類,重度為26.7kN/m3,彈性模量為1GPa,泊松比為 0.35,黏聚力為0.13MPa,摩擦角為23°。

在建模分析時,選取洞身段具有代表性的一部分段落(包含其影響范圍內的巖體)進行模擬分析研究。在選用特征值分析研究時模型邊界視為彈性邊界,在選用時程分析研究時模型邊界阻尼邊界。

3.2.1 彈性邊界狀況

MIDAS/GTS 通過選取曲面彈簧定義彈性邊界的方法進行特征值分析時,彈簧系數選用日本鐵道路規范中的地基反力系數方法的進行計算。

豎直地基反力系數的計算公式如下:

(5)

水平地基反力系數的計算公式如下:

(6)

式中:α為相關系數,取 0.1;E為巖體彈性模量值;Av為地基豎直方向上的截面積值;Ah為地基水平方向上的截面積值。

3.2.2 阻尼邊界狀況

選用1972年Lysmer和Wass提出的關于人工黏性阻尼邊界狀況的理論,在計算分析過程中模型邊界上施加人為阻尼器。為了擬定黏性邊界條件狀況,需計算分析相應巖體所有方向上相對應的單位面積上的阻尼系數[10]。其計算公式如下:

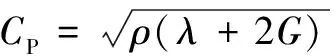
(7)

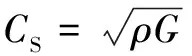
(8)

(9)

(10)

式中:CP為P波單位面積上的阻尼系數值;CS為S 波單位面積上的阻尼系數值;ρ為圍巖的密度值;λ為體積的彈性模量值;G為剪切彈性模量值;E為彈性模量值;μ為泊松比值。

通過式(7)和式(8)的計算可知,本Ⅳ級巖體計算模型中的單位面積上的阻尼系數值分別是CP=2026.9kPa·s/m,CS=973.7kPa·s/m。

3.3 計算斷面及荷載布置

為檢測間隔裝藥結構的爆破減振效果,在隧洞開挖過程中分段進行爆破,并在黑河引水1號洞選取8個斷面(見圖5中J1～J8)對裝藥結構爆破振動實時監測。在 MIDAS-GTS有限元數值分析軟件中選取黑河引水1號洞拱頂 (A節點),隧洞左側壁(D 節點),隧洞右側壁(B節點),隧洞底板中點(C節點)四個節點(見圖6)作為歷程測點,分別在一到六期(即距開挖洞口4m,8m,12m,16m,20m,40m,見圖7和圖8)爆破荷載情況下,計算五點豎直與水平徑向振動速度,觀察結果進行比對。

圖5 監測斷面選擇

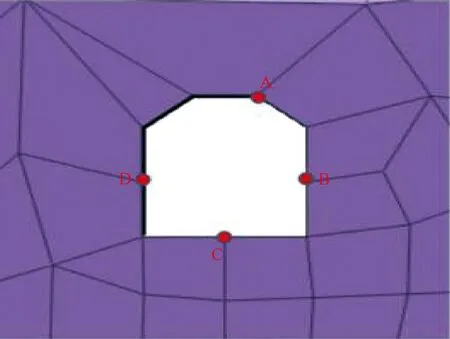
圖6 監測點選擇

圖7 爆破斷面選擇

圖8 爆破斷面與監測斷面之間距離示意圖

4 計算結果及分析

4.1 六期爆破質點振速分析

根據動力有限元分析結果,基于一到六期爆破荷載分別對已有洞室8個斷面上四點(A:頂部、B:右側壁、C:底板、D:左側壁)的振速影響分析,一期相同荷載在不同位置下隨質點振動速度隨時間變化關系見圖9～圖12。

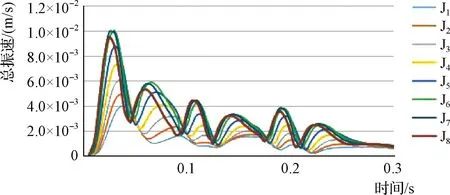
圖9 一期爆破右側壁(B點)總振速衰減模擬波形圖

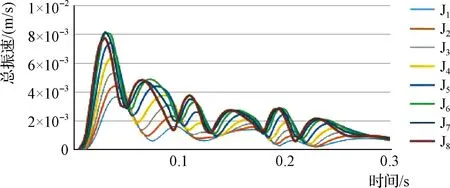
圖10 一期爆破頂部(A點)總振速衰減模擬波形圖

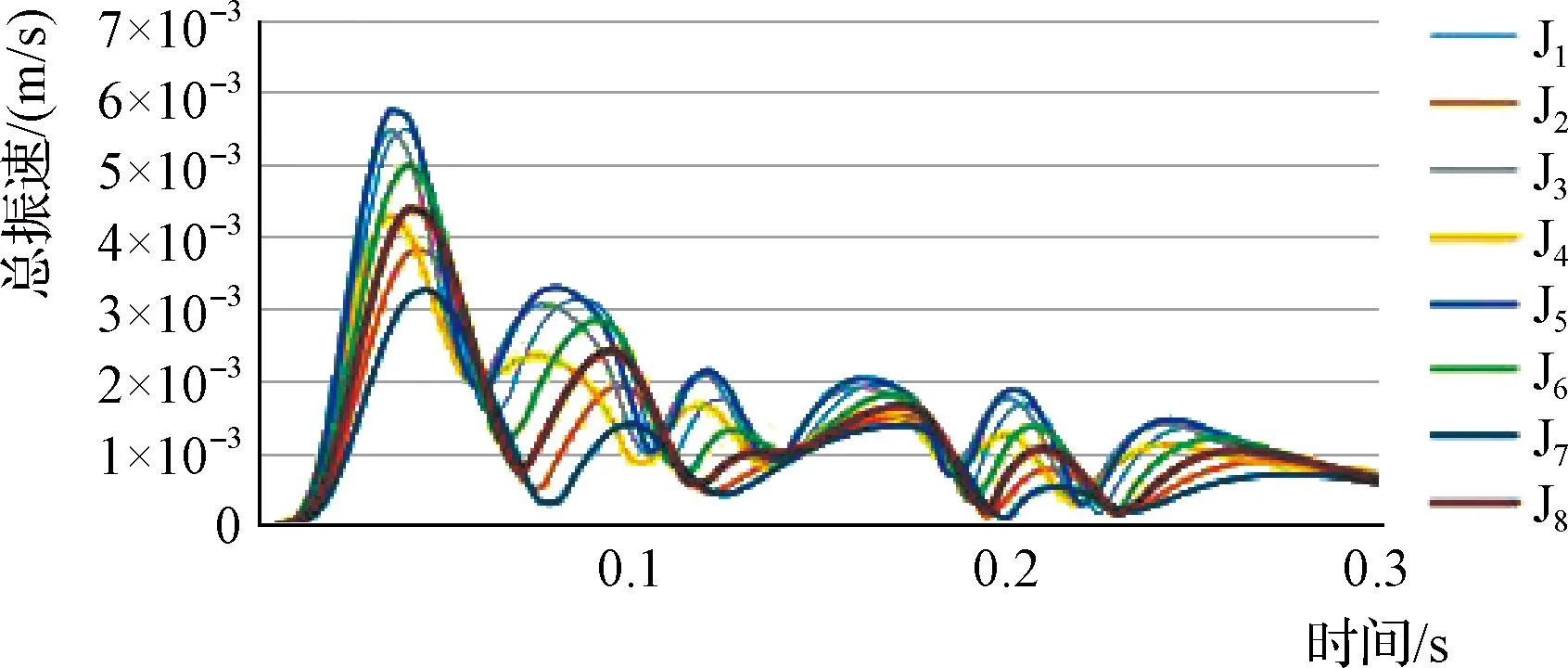
圖11 一期爆破左側壁(D點)總振速衰減模擬波形圖

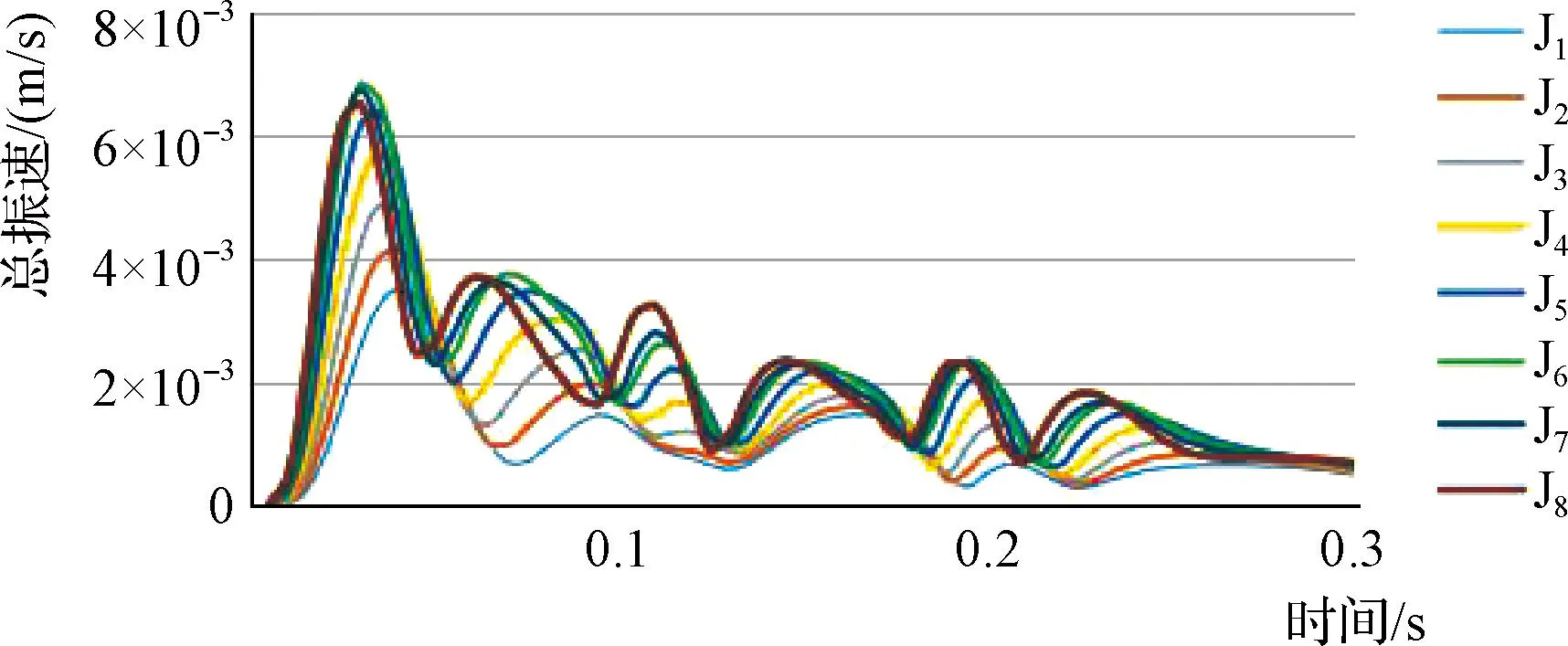
圖12 一期爆破底板(C點)總振速衰減模擬波形圖

右拱側(B 點)振速分析:六期爆破荷載影響均首先到達右拱側(B 點),其中:一至三期爆破荷載均在施加荷載 0.03s后,右拱側(B 點)振速達到最大,而四至六期爆破荷載則分別在施加荷載0.035s、0.065s、0.09s后,右拱側(B 點)振速出現峰值。右拱側(B 點)受到的爆破影響最快且最大,這是由于右拱側(B 點)距離爆振荷載施加位置距離最近。

拱頂(A 點)與底板(C點)振速分析:六期爆破荷載影響經過右拱側(B 點)后,拱頂(A 點)與底板(C點)振速幾乎同時達到最大,其中:一期爆破荷載是在施加荷載0.03s后,二至四期爆破荷載是在施加荷載0.035s后,五期、六期爆破荷載分別是在施加荷載0.075s、0.095s后,拱頂(A 點)和底板(C點)振速同時出現峰值。

左拱側(D 點)振速分析:一期爆破荷載在施加荷載0.035s后、二至四期爆破荷載在施加荷載0.04s后、五期爆破荷載在施加荷載0.09s后、六期爆破荷載在施加荷載0.105s后,左拱側(D 點)達到最大振速。

黃池溝爆破荷載最早到達黑河隧洞右拱側 (B 點),同時質點振動速度也達到最大,后經洞室自由面反射與后到應力波進行疊加,洞壁質點振動速度值逐漸衰減。

4.2 各測點最大振速分析

在各級隧洞開挖爆破施工過程中,六期爆破荷載下黑河引水1號洞襯砌各關鍵點最大振動速度變化見表1和圖13。

表1 六期爆破荷載下各關鍵點最大振速對比 單位:m/s

圖13 六期爆破荷載下各關鍵點振速峰值變化情況

由圖13可知,A、B、C、D分別代表黑河引水1號洞拱頂、右側壁、底板中點、左側壁,可以看出距離開挖洞最近的B點,即右側壁振速最大,最大振速為0.01m/s; 隨著開挖進程推進,振速逐步減小,影響最大的B點到五期開挖即距開挖洞口20m處時,振速僅為一期開挖即據開挖洞口4m處時的35.4%,到六期開挖即距開挖洞口40m處時,振速僅為一期開挖即據開挖洞口4m處時的18.7%。

5 結 論

本文根據黃池溝黑河供水連通洞出口段與黑河引水1號洞的關系,采用三維動力有限元分析方法開展了黃池溝隧洞爆破施工下黑河隧洞襯砌振動效應分析,主要結論如下:

a.在各級隧洞開挖爆破施工過程中,黑河引水1號洞襯砌各關鍵點振動速度隨著與爆破荷載距離增大而逐漸減小,距離黑河引水1號洞最近的右側壁(B點)振速最大,拱頂,左拱側,底板逐漸衰減。

b.在各級爆破開挖施工過程中,黑河引水1號洞的襯砌最大振速為0.129～1.004cm/s,低于規范允許的7～15cm/s,襯砌結構的安全是有保障的。

c.黑河引水1號洞襯砌的最大振速發生在黃池溝黑河供水連通洞洞口段10m范圍內的爆破施工階段。