基于國密SM2算法的局部可驗證聚合簽名算法研究

沈榮耀 馬利民 王佳慧 張 偉

1(北京信息科技大學北京未來區塊鏈與隱私計算高精尖中心 北京 100101)

2(北京信息科技大學計算機學院 北京 100101)

3(北京信息科技大學國家經濟安全預警工程北京實驗室 北京 100101)

4(國家信息中心信息與網絡安全部 北京 100045)

數字簽名是一種可以有效保障網絡安全的密碼技術,廣泛應用于我國政府、金融、商業等領域.在實際場景中,會持續產生海量的數字簽名,占據大量存儲空間,且對簽名逐個驗證會帶來較大計算開銷,因此,如何提高海量簽名的驗證效率,降低簽名存儲占用顯得尤為重要.

由于聚合簽名(aggregate signature, AS)可以提高批量驗證效率,降低存儲占用,所以尤其適用于解決大量簽名的存儲以及驗證的問題.聚合簽名由Boneh等人[1]于2003年首次提出.然而,對聚合簽名驗證時,驗證方需要獲取完整明文集合,當聚合的簽名數量較多時,驗證聚合簽名所需明文數量也隨之增大.有時驗證方僅需驗證指定明文,獲取完整明文集合會為驗證方增加計算負擔.針對這種情況,采用局部可驗證的聚合簽名可以大大降低驗證方的計算負擔.局部可驗證的聚合簽名由Goyal等人[2]首次提出.

SM2算法[3]由國家密碼管理局于2010年底發布,是一種基于橢圓曲線的密碼算法,其具有自主可控、安全性高、易于實現等優點,廣泛應用于各類信息系統之中.

本文提出一種安全、高效的基于國密SM2的局部可驗證聚合簽名方案.方案采用聚合簽名技術,提高批量驗證效率,同時采用局部可驗證技術,使驗證方對聚合簽名及指定明文驗證時,無需獲取全部明文,僅需短提示即可,進一步降低驗證方計算成本.

1 相關工作

根據采用的公鑰密碼體制,聚合簽名可以劃分成3類:基于身份的聚合簽名(identity-based aggregate signature, IBAS)、無證書聚合簽名(certificateless aggregate signature, CLAS)以及基于公鑰基礎設施(public key infrastructure, PKI)的聚合簽名.

1) 基于身份的聚合簽名:2006年,Gentry等人[4]提出一種高效的IBAS方案,然而該方案需要所有簽名者共享狀態信息,使應用場景受到限制;2007年,Boldyreva等人[5]提出有序IBAS方案,克服了Gentry方案的共享問題;2016年,Muranaka等人[6]改進了Boldyreva方案,針對動態源路由協議提出有序IBAS方案,該方案相較于Boldyreva方案,計算性能明顯提高;2019年,Kojima等人[7]在Muranaka方案基礎上進行改進,引入分布式密鑰生成中心(key generation center, KGC),消除集中式KGC;2020年,安濤等人[8]針對車輛自組織網(vechicular adhoc network, VANET)提出一種基于國密SM9算法的IBAS方案,然而該方案聚合簽名長度和簽名車輛數量呈線性相關,導致通信開銷較大.基于身份的聚合簽名雖然性能較好,但是其密鑰生成必須借助可信第三方,導致密鑰托管的問題無法避免.

2) 無證書聚合簽名:2018年,Kumar等人[9]針對醫療無線傳感器網絡(healthcare wireless sensor networks, HWSNs)構造CLAS方案,該方案計算開銷小于其他同類方案;2019年,Kumar等人[10]針對VANET,在其之前方案[9]上構造CLAS方案,通過偽身份實現車輛的隱私保護;2022年,蒙彤等人[11]針對HWSNs提出支持并行密鑰隔離CLAS方案,有效降低HWSNs系統的延遲.無證書聚合簽名方案中部分私鑰由半可信的第三方生成,另一部分私鑰由用戶自身產生,所以消除了密鑰托管問題.當前大部分CLAS方案中都基于雙線性對,導致效率較低,實用性較差.

3) 基于公鑰基礎設施的聚合簽名:2019年,Verma等人[12]針對醫療監控提出無配對的基于證書的AS方案,然而該方案存在聚合簽名長度與簽名者數量呈線性相關的問題;同年,Verma等人[13]提出另一種基于證書的AS方案,該方案聚合簽名更為緊湊;2021年,Verma等人[14]針對物聯網環境提出無配對的基于證書的短聚合簽名方案,計算開銷更小;同年,Zhu等人[15]分析文獻[14]方案安全缺陷,針對無線醫療傳感器網絡提出一種支持用戶匿名保護的基于證書的AS方案并證明其安全性.基于公鑰基礎設施的聚合簽名需要對證書的管理付出一定的代價,由于PKI已經廣泛應用于各種現實場景中,因此基于PKI的聚合簽名可以更好地與已部署的公鑰基礎設施相結合.

2022年,Goyal等人[2]針對驗證者驗證指定明文和聚合簽名時,仍需獲取完整明文集合的問題,提出局部可驗證聚合簽名的概念.驗證方對聚合簽名驗證時,無需完整明文集合,僅需指定消息及對應短提示即可,并給出基于RSA以及雙線性對的2種局部可驗證聚合簽名構造方案,并證明其安全性.

2 基于SM2的局部可驗證聚合簽名方案

本文基于聚合簽名和局部可驗證簽名的思想,對SM2算法進行適當的改造,提出了一種基于國密SM2算法的局部可驗證聚合簽名方案(locally verifiable aggregate signature scheme based on SM2, SM2-LVAS).形式化地表示為SM2-LVAS=(Setup,Key-Gen,Sign,Verify,Aggregate-Signature,Aggregate-Verify,Local-Open,Local-Aggregate-Verify),算法共8個步驟.

2.1 系統建立

定義大素數p,Fp為有限域,a,b∈Fp為橢圓曲線E的參數,橢圓曲線上的基點(x,y),其中x,y∈Fp,n為群G的階,Hv()為摘要長度為v(單位為b)的哈希算法.

2.2 密鑰生成

SM2算法密鑰生成流程如下:

1) 選取隨機數d,并且d∈[1,n-2];

2) 計算P=dG,則其公私鑰對為(P,d).

2.3 單個SM2簽名

假設簽名者為A,其公私鑰對為(PA,dA),對于待簽名消息Mi,隨機選取ki∈[1,n-1].

1) 計算ZA=H256(ENTLA‖IDA‖a‖b‖xG‖yG‖xA‖yA),其中IDA為用戶可辨識標識,ENTLA為IDA長度轉化而成的2B數據;

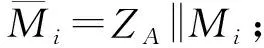
4) 計算(xi,yi)=kiG;

5) 計算ri=(ei+xi) modn;

6) 計算si=((1+dA)-1·(ki-ridA)) modn;

7) 計算vi=(ei+yi) modn.

單個簽名為(ri,si,vi).

2.4 單個SM2驗簽

對收到的消息Mi及其數字簽名(ri,si,vi)進行驗簽,其過程如下:

1) 檢驗ri,si,vi∈[1,n]是否成立,若不成立,則驗證不通過;

2) 計算ZA=H256(ENTLA‖IDA‖a‖b‖xG‖yG‖xA‖yA);

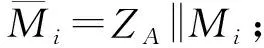
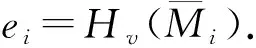
5) 計算ti=(ri+si) modn;

6) 計算(xi,yi)=siG+tiPA;

7) 計算R′=(ei+xi) modn.

檢查R′=ri是否成立,成立則驗證通過,否則失敗.

2.5 簽名聚合

消息集合{M1,M2,…,Mi,…,ML}的數字簽名為{(r1,s1,v1),(r2,s2,v2),…,(ri,si,vi),…,(rL,sL,vL)}.簽名聚合過程如下:

1) 計算E=Hv(e1‖e2‖…‖eL);

2) 計算xi=(ri-ei) modn;

3) 計算yi=(vi-ei) modn;

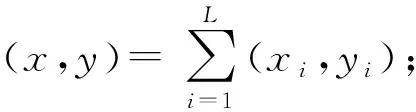
5) 計算R=(E+x) modn;

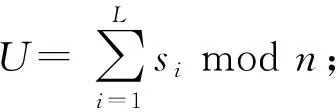
7) 計算ti=(ri+si) modn;

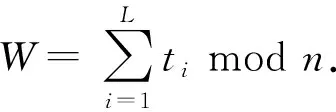
聚合簽名為σ=(R,U,W,t1,t2,…,tL).

2.6 聚合驗證

驗證方收到消息集合{M1,M2,…,Mi,…,ML}和聚合簽名σ.聚合驗證過程如下:

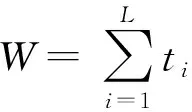
2) 計算ZAi=H256(ENTLAi‖IDAi‖a‖b‖xG‖yG‖xAi‖yAi);

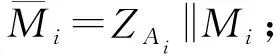
5) 計算d=Hv(e1‖e2‖…‖eL);

7) 計算R′=(d+x) modn.

當簽名者相同時,橢圓曲線上的點(x,y)的計算可簡化為(x,y)=UG+WPA.

檢查等式R′=R是否成立,若成立則驗證通過,否則驗證失敗.

2.7 提示生成

提示生成算法一般由存儲服務器或簽名聚合方進行計算.通過消息明文集合計算得到指定消息的短提示auxj.提示生成過程如下:

1) 計算ZAi=H256(ENTLAi‖IDAi‖a‖b‖xG‖yG‖xAi‖yAi);

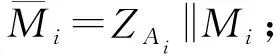
4) 計算E=Hv(e1‖e2‖…‖eL);

5) 計算auxj1=(E-ej) modn;

6) 計算h1=Hv(auxj1);

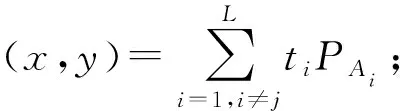
8) 計算auxj2=(h1+x) modn;

9) 計算auxj3=(h1+y) modn;

10)輸出短提示auxj=(auxj1,auxj2,auxj3).

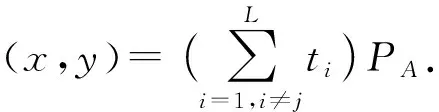
2.8 局部驗證

驗證方收到指定消息明文Mj、聚合簽名σ和短提示auxj.局部驗證過程如下:

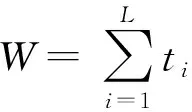
2) 計算ZAj=H256(ENTLAj‖IDAj‖a‖b‖xG‖yG‖xAj‖yAj);

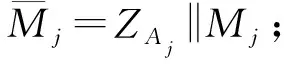
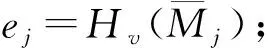
5) 計算d=(auxj1+ej) modn;

6) 計算h1=Hv(auxj1);

7) 計算xj=(auxj2-h1) modn;

8) 計算yj=(auxj3-h1) modn;

9) 計算(x,y)=(xj,yj)+UG+tjPAj;

10) 計算R′=(d+x) modn.

檢查等式R′=R是否成立,若成立則驗證通過,否則驗證不通過.

3 方案分析

3.1 正確性分析

令E=Hv(e1‖e2‖…‖eL),則相同簽名者時的聚合驗證公式為

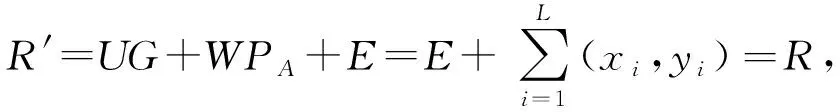
(1)

則只需驗證

(2)

其證明過程如式(3)所示.不同簽名者時及局部驗證時的證明過程與相同簽名者時相似,不再贅述.

(3)

3.2 安全性分析

SM2-LAVS方案單個SM2簽名步驟,相較于標準SM2算法簽名流程,對于明文Mi,生成簽名由(ri,si)變為(ri,si,vi),其中vi=(ei+yi).如果敵手得到明文Mi哈希值ei,則可計算出yi,而在SM2算法標準驗簽流程中,檢驗

R′=(ei+xi)=ri,

(4)

其中xi通過(xi,yi)=siG+tiPA計算得到.由此可知,敵手可通過一定的計算得到簽名時的xi,yi,因此,在單個SM2簽名步驟中新增vi字段并不會使本文方案安全性低于SM2標準算法.

在聚合驗證步驟時,需要驗證

(5)

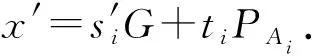
(6)

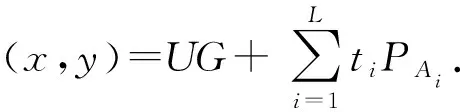
在局部驗證步驟時,需要驗證

R′=R,

(7)

auxj1+ej+x=R.

(8)

4 方案實現與性能分析

本文使用C++語言實現SM2-LAVS方案并調用GmSSL庫實現SM2中橢圓曲線上計算.實際開發環境中CPU為Intel i5-9400,內存為8GB,操作系統為Ubuntu 18.04.

表1定義了密碼運算的符號,并通過重復運行1000次運算取其平均值的方法得出單次運算所消耗時間.

表1 單次密碼運算所消耗時間 ms

表2分析了在相同簽名者和不同簽名者2種情況下各個步驟計算成本對比.

表3對比了幾種聚合簽名方案及本文方案的計算成本.

圖1所示為不同聚合簽名方案聚合驗證時間開銷對比.

由圖1可知,隨著明文消息數量增大,本文方案聚合驗證開銷在幾個方案中最小,因此,本文方案與同類方案相比,具有較高性能.

表2 各個步驟計算成本對比

表3 各個聚合簽名方案計算成本對比

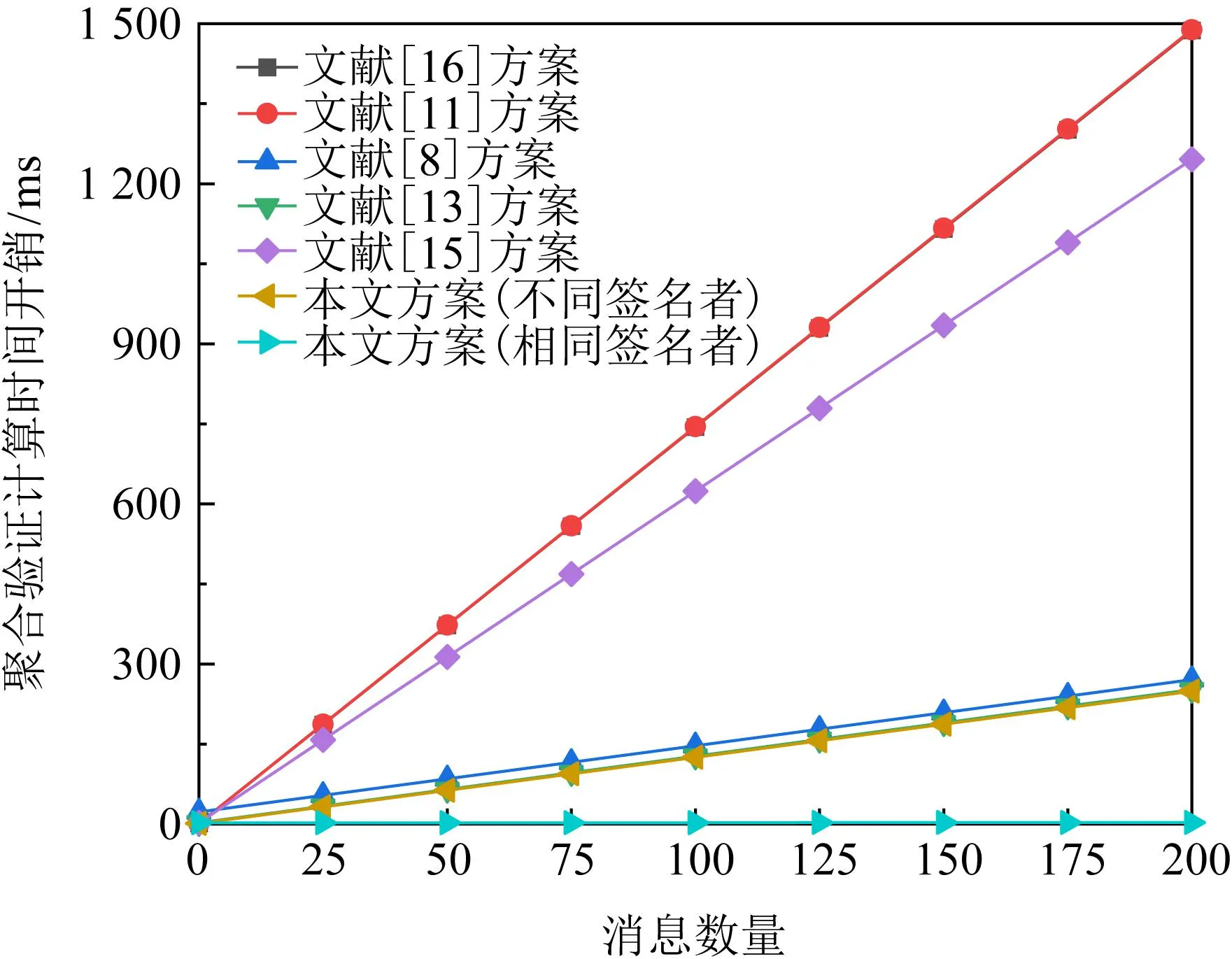
圖1 不同聚合簽名方案時間開銷對比

5 結 語

本文基于國密SM2算法設計一種局部可驗證聚合簽名方案,利用聚合簽名提高驗證方驗證效率,通過局部可驗證使驗證方對聚合簽名及指定明文驗證時,無需獲取全部明文.通過與現有若干個聚合簽名方案對比,證明本文方案聚合驗證開銷更低,具有一定優勢.但本文方案聚合簽名長度與簽名者數量呈線性相關,將來可以進一步優化,將簽名長度優化為常量值,降低通信開銷.