帶色散的四階拋物型方程的緊致差分格式

李冉冉,王紅玉,開依沙爾·熱合曼

(新疆大學 數學與系統科學學院,新疆 烏魯木齊 830046)

帶色散的四階拋物型方程是色散方程與四階拋物型方程的結合,在擴散、滲流、熱傳導等領域得到廣泛應用。在過去的幾十年里,研究者們對該類拋物型偏微分方程進行了大量的理論和數值研究,由于帶色散的四階拋物型方程的精確解一般不容易得到,因此相關的數值處理引起了許多學者的關注。因此,對帶色散的四階拋物型方程構造高精度穩定的數值格式是非常重要的問題之一。

本研究考慮如下一維帶色散的四階拋物型方程的初邊值問題:

(1)

式中:α、β為常系數且不同時為零,f、g1、g2為已知充分光滑的函數,u為待求未知量。

三階、四階空間導數項常見于復雜的偏微分方程,如KdV方程、RLW方程、Kuramoto-Sivashinsky方程等,因而許多學者對包含高階導數項的偏微分方程的數值格式進行了研究[1-11]。文獻[1]用局部間斷Petrov-Galerkin和TVDRK3方法求解了非線性色散方程;文獻[2]對該類方程構造了時間方向上具有二階精度、空間方向上具有四階精度的差分格式;文獻[3]針對KdV方程的初邊值問題構造了時間和空間方向上都具有二階精度的差分格式;文獻[4]提出一種求解廣義Rosenau-KdV方程的有限差分方法,數值結果表明該方法在時間和空間方向上分別達到了二階和四階的精度;文獻[5]提出一種時間二階精度、空間四階精度的差分格式來求解Rosenau-KdV-RLW方程;文獻[6]結合四階差分格式和TVDRK3方法求解了Kuramoto-Sivashinsky方程,文獻[7]對該類方程構造了時間二階精度、空間四階精度的差分格式;文獻[8-12]給出色散方程和四階拋物型方程的各種數值方法,不過這些數值方法僅適用于周期邊界條件;文獻[13]給出了兩點邊值問題的四階緊致差分格式,文獻[14-15]將該格式應用到了Burgers方程的數值模擬中;文獻[16]對雙曲型電信方程的空間變量用四階緊致差分格式,時間變量采用三次Hermite插值法,提出求解該方程的四階精度的格式。本研究結合四階緊致差分格式和三次Hermite插值法,構造出帶色散的四階拋物型方程的時間空間都具有四階精度的無條件穩定的差分格式。

1 空間離散

(2)

將式(2)寫作矩陣形式:

LxU′=MxU+b1。

(3)

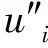
(4)

式(4)寫作矩陣形式:

LxxU″=MxxU+b2。

(5)

利用式(3)和式(5),空間變量的三階、四階導數的近似有:

(6)

(7)

將式(6)和式(7)代入方程(1),得到常微分方程組:

(8)

2 三次Hermite插值法

三次Hermite插值多項式Q(x)可以寫成[17]:

Q(x)=w(x0)v0(x)+w(x1)v1(x)+w′(x0)V0(x)+w′(x1)V1(x)。

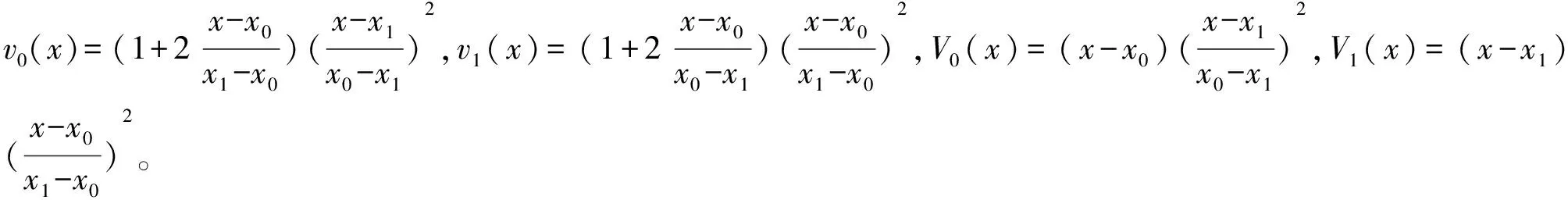
在下列定理1中,給出了三次Hermite插值的誤差。

定理1[17]設有兩個不同的點x0、x1,且w∈C4[x0,x1]。如果Q(x)是三次Hermite插值多項式,則在區間[x0,x1]中的每個x都對應于[x0,x1]中的一個點η,有

(9)

根據等式(9)和定理1,可以得到積分公式:

(10)

常微分方程(8)應用三次Hermite插值法(10),則在Dirichlet邊界下的帶色散的四階拋物型方程(1)的差分格式:

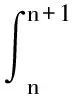
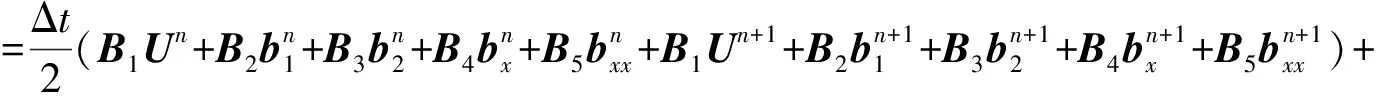
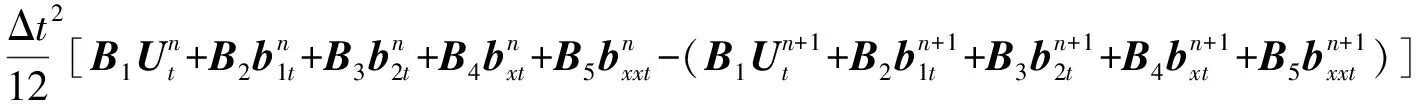
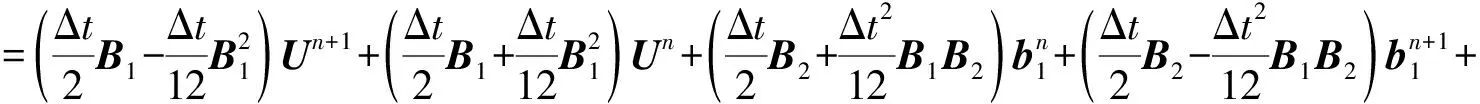
(11)

因此,式(1)的差分格式為:

(12)

3 穩定性分析

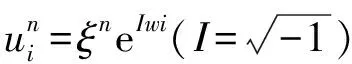
(13)

將式(13)代入格式(12),有

顯然S2≥0,因此|ξ|≤1,表明使用式(6)和式(7)近似式(1),格式(12)是無條件穩定的。

4 數值實驗

為了驗證本研究格式的可靠性,用所提方法進行數值計算,給出數值算例的各種誤差及收斂階。其中,L∞、L2誤差和收斂階的定義如下。

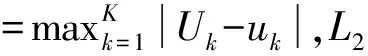
數值例子1色散方程

表1中給出色散方程在不同Δx、Δt下,當T=2時的格式(12)的L∞、L2誤差和收斂階。從數值結果可以看出該格式在空間和時間方向上都達到了預期的四階精度。表2針對色散方程在T=2,Δx=1/40下,給出不同Δt時L2誤差和收斂階對比。可以看出,當空間變量離散為式(8),時間變量離散為Crank-Nicolson格式時時間方向只有二階精度,本研究格式可以達到四階精度,且具有更小的誤差。

表1 T=2時不同Δx、Δt時的L∞、L2誤差和收斂階

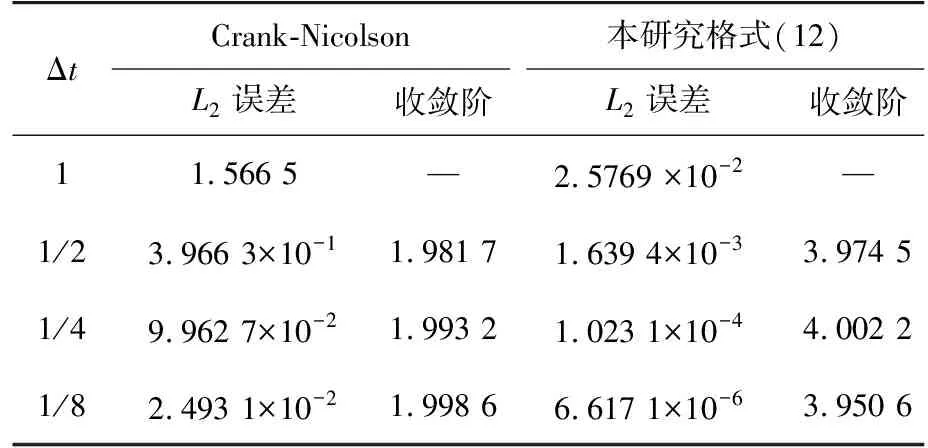
表2 T=2、Δx=1/40,不同Δt時的L2誤差和收斂階比較

數值例子2四階拋物型方程

表3給出四階拋物型方程在不同Δx、Δt下,當T=8時的本研究格式(12)的L∞、L2誤差和收斂階。結果表明該格式在空間和時間方向上都具有四階精度,這與格式的理論結果相吻合。表4中對該方程給出空間變量離散為式(8),時間變量離散為Crank-Nicolson格式和本研究格式(12)的L2誤差及時間方向收斂階的對比,數值結果表明三次Hermite插值法比Crank-Nicolson更具有精確性。

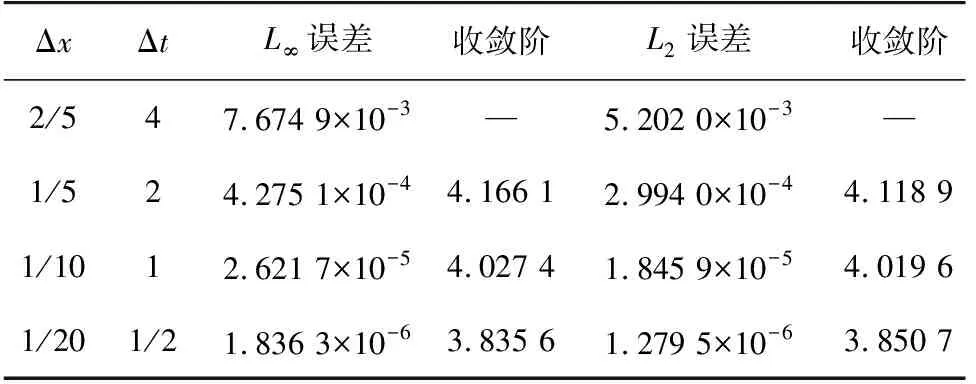
表3 T=8時不同Δx、Δt時的L∞、L2誤差和收斂階

表4 T=4、Δx=1/10,不同Δt時的L2誤差和收斂階比較

數值例子3帶色散的四階拋物型方程

表5中給出了帶色散的四階拋物型方程在不同Δx下,當T=1時刻的本研究格式(12)上的L∞、L2誤差及其收斂階。從數值結果可以看出,該格式在空間方向上達到四階精度,且隨著Δx的減小,計算結果更精確。表6中給出空間變量離散為式(8)、時間變量離散為Crank-Nicolson格式和本研究格式(12)的L2誤差及時間方向收斂階的比較,數值結果表明本研究格式的L2誤差比Crank-Nicolson格式小2～4個數量級,說明研究的格式具有更高的精度。

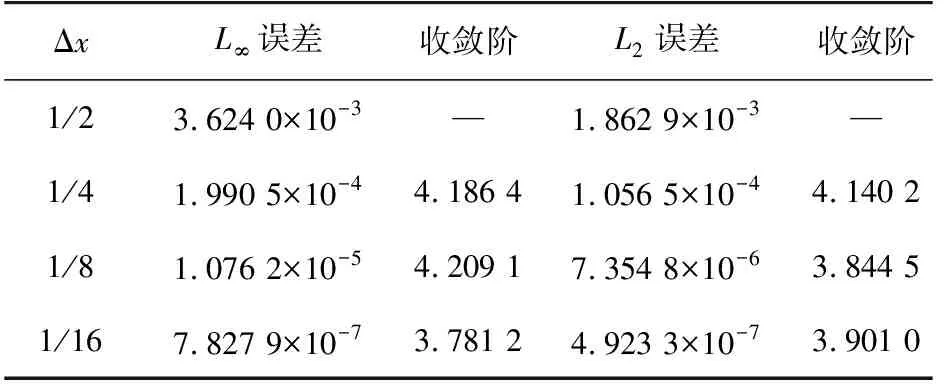
表5 T=1、Δt=Δx,不同Δx時的L∞、L2誤差和收斂階

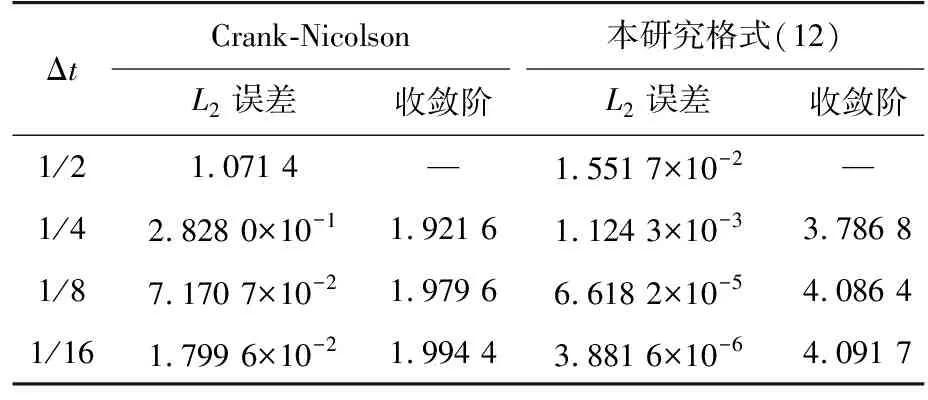
表6 T=1、Δx=1/10,不同Δt時的L2誤差和收斂階比較

5 結論

本研究針對具有Dirichlet邊界條件的帶色散的四階拋物型方程,空間的三階導數項和四階導數項用四階精度緊致格式離散,時間方向利用三次Hermite插值法,構造出一種時間空間同時具有四階精度的無條件穩定的差分格式,用傅里葉方法證明了所提格式的無條件穩定性。數值實驗中采用本格式分別計算了色散方程、四階拋物型方程、帶色散的四階拋物型方程等三種類型方程的算例,并與該三類方程的Crank-Nicolson格式進行了數值比較,結果表明本研究格式比Crank-Nicolson格式更具有精確性。從表1、表3、表5可知,本格式在空間方向上達到了四階的精度;從表2、表4、表6可知,本格式在時間方向上也達到了四階精度,數值結果與理論相符合。另外,該格式可以通過利用局部一維化方法推廣到二維和三維帶色散的四階拋物型方程問題的數值計算上。