炮口振動(dòng)特性對(duì)自動(dòng)炮射擊精度的影響研究

王二亮,劉 丹,王宏金,高 英,任弘毅

(西北機(jī)電工程研究所, 陜西 咸陽 712099)

0 引言

研究火炮結(jié)構(gòu)振動(dòng)對(duì)射擊精度的影響,可以從結(jié)構(gòu)層面上為火炮的射擊提供良好的外彈道炮口擾動(dòng)初始條件,從而提高射擊精度[1]。炮口振動(dòng)是影響自動(dòng)炮射擊精度的一個(gè)重要因素[2],在不考慮武器和彈藥自身的內(nèi)彈道和外彈道的設(shè)計(jì)精度影響,連發(fā)射擊精度主要取決于火炮系統(tǒng)的安裝間隙、搖架間隙、后座長度和后座軸向精度、載體和托架等剛強(qiáng)度等。因此通過優(yōu)化火炮系統(tǒng)的結(jié)構(gòu)設(shè)計(jì),改善彈丸出炮口一致性,可以有效控制火炮系統(tǒng)的射擊精度。許多科研人員考慮了身管柔性、結(jié)構(gòu)非線性等因素對(duì)火炮射擊時(shí)的炮口振動(dòng)特性進(jìn)行研究[3-6],以期提高火炮系統(tǒng)的射擊精度。

火炮作為一個(gè)結(jié)構(gòu)復(fù)雜、運(yùn)動(dòng)自由度多的機(jī)械系統(tǒng),傳統(tǒng)的動(dòng)力學(xué)分析方法已經(jīng)遠(yuǎn)不能滿足對(duì)其進(jìn)行振動(dòng)分析的需要。隨著科學(xué)技術(shù)的發(fā)展,多體動(dòng)力學(xué)已成熟應(yīng)用于汽車、機(jī)床、兵器等機(jī)械工程領(lǐng)域[7-9]。許多科研人員將火炮發(fā)射動(dòng)力學(xué)與多體動(dòng)力學(xué)相結(jié)合,用于研究火炮射擊振動(dòng)特性。王德石等[10]研究了火炮系統(tǒng)的沖擊響應(yīng)規(guī)律及固有振動(dòng)特性,獲得了火炮振動(dòng)與其結(jié)構(gòu)參數(shù)的內(nèi)在聯(lián)系,有效改善了火炮的振動(dòng)性能。張世明等[11]建立了中口徑自動(dòng)炮非線性動(dòng)力學(xué)有限元模型,能夠有效地反應(yīng)火炮射擊時(shí)的振動(dòng)特性,為中口徑埋頭彈火炮武器系統(tǒng)射擊密集度優(yōu)化提供參考。Jie等[12]分析了影響射擊密集度的浮動(dòng)機(jī)構(gòu)參數(shù),建立了剛?cè)狁詈隙囿w動(dòng)力學(xué)模型,對(duì)某榴彈機(jī)槍系統(tǒng)的二十發(fā)射擊過程進(jìn)行了仿真分析。王紅巖[13]則考慮了底盤振動(dòng)對(duì)射擊精度的影響。筆者為了進(jìn)一步探究火炮結(jié)構(gòu)振動(dòng)對(duì)射擊精度的影響,在火炮發(fā)射動(dòng)力學(xué)理論的基礎(chǔ)上,考慮自動(dòng)炮各部件之間的約束關(guān)系及身管柔性,建立了剛?cè)狁詈献詣?dòng)炮虛擬樣機(jī)模型,并進(jìn)行發(fā)射動(dòng)力學(xué)仿真,初步計(jì)算了射擊密集度,為自動(dòng)炮優(yōu)化設(shè)計(jì)提供參考依據(jù)。

1 自動(dòng)炮虛擬樣機(jī)建模

1.1 基本假設(shè)及系統(tǒng)拓?fù)浣Y(jié)構(gòu)分析

根據(jù)自動(dòng)炮的結(jié)構(gòu)特點(diǎn)及射擊過程各部件的運(yùn)動(dòng)規(guī)律,在不影響模型合理性的前提下,為便于理論分析,作如下假設(shè):

1) 除火炮身管外,炮塔及武器系統(tǒng)中各構(gòu)件均作剛體處理;

2) 忽略車體及地面的影響,自動(dòng)炮底座直接固定在臺(tái)架上;

3) 考慮身管與火炮前支撐架間隙和摩擦非線性因素的影響;

4) 不考慮供輸彈機(jī)構(gòu)的影響,連發(fā)射擊時(shí),每發(fā)彈丸已輸送到射擊位置;

5) 射擊時(shí)受到主動(dòng)力為火藥氣體壓力、緩沖彈簧提供的后坐阻力和復(fù)進(jìn)力,不考慮自動(dòng)機(jī)工作時(shí)自動(dòng)機(jī)零部件間接觸/碰撞的能量損耗,自動(dòng)機(jī)作為后坐部分參與運(yùn)動(dòng)。

火炮射擊時(shí),擊針擊發(fā)底火后,火藥氣體壓力推動(dòng)彈丸向前運(yùn)動(dòng),同時(shí)作用在炮閂底面,使自動(dòng)機(jī)閂體、炮尾、身管等部件沿著搖架導(dǎo)軌一起后坐,同時(shí)受到緩沖彈簧阻力的作用,后坐到位后,在緩沖彈簧復(fù)進(jìn)力的作用下完成復(fù)進(jìn)運(yùn)動(dòng)。后坐力通過搖架、緩沖彈簧作用在自動(dòng)炮架座上,并傳給固定臺(tái)架。圖1為主要部件間的約束關(guān)系。

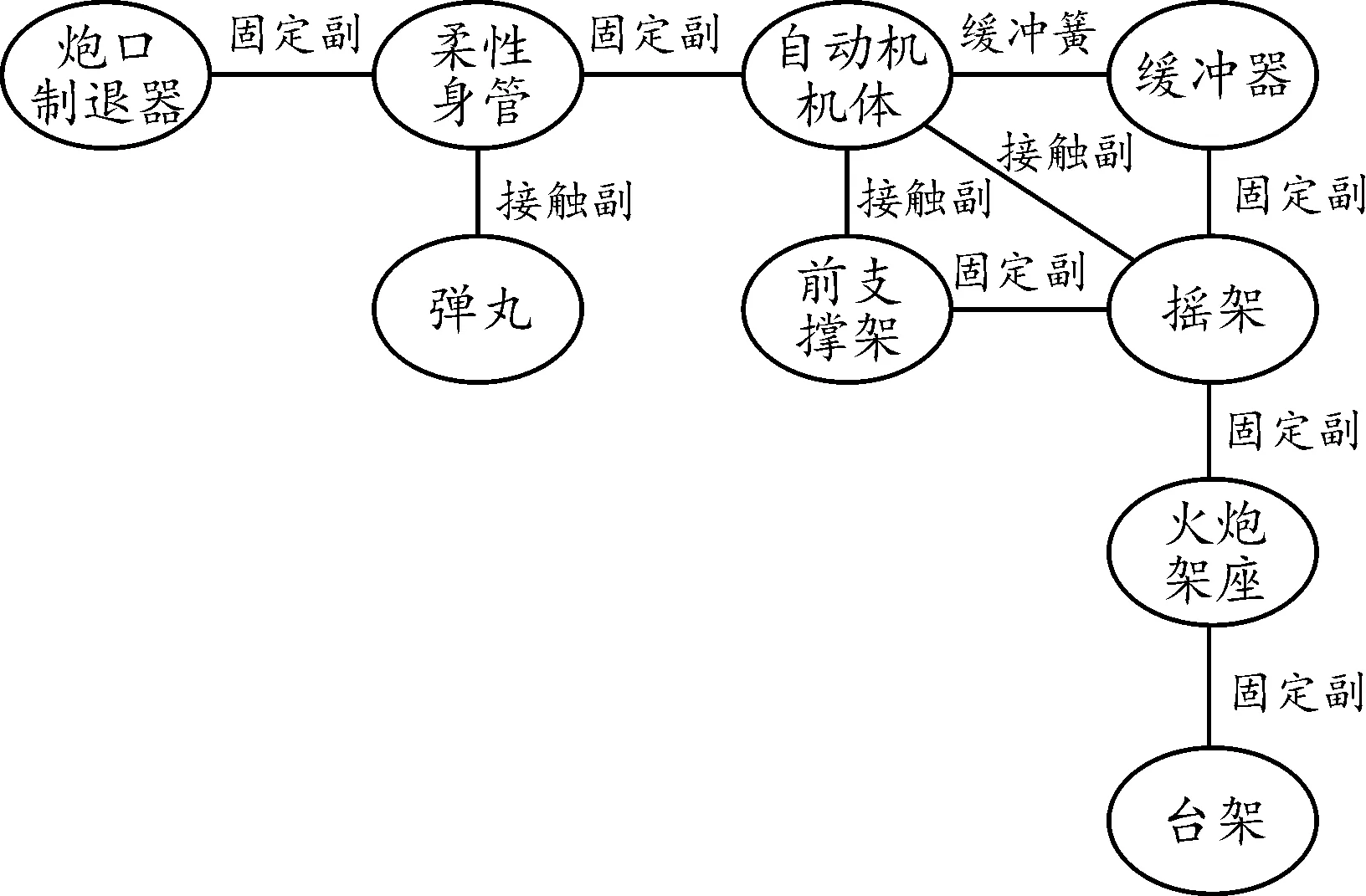
圖1 自動(dòng)炮主要部件間的約束關(guān)系

1.2 動(dòng)力學(xué)特性仿真模型

三維實(shí)體模型的作用是為動(dòng)力學(xué)分析提供各零部件的幾何形狀、裝配關(guān)系、全炮的質(zhì)量、質(zhì)心位置和轉(zhuǎn)動(dòng)慣量等。由于自動(dòng)炮系統(tǒng)各零部件外形比較復(fù)雜,文中利用三維建模軟件建立其實(shí)體模型,將各零部件進(jìn)行裝配,獲得裝配模型,再根據(jù)系統(tǒng)仿真模型的約束關(guān)系,將各子部件以動(dòng)力學(xué)軟件能識(shí)別的格式導(dǎo)出,并建立動(dòng)力學(xué)特性仿真模型。

根據(jù)假設(shè),建模時(shí)將自動(dòng)炮身管為柔性體。火炮射擊時(shí)身管會(huì)產(chǎn)生較大的變形,建立柔性體模型可分析身管的彈性變形對(duì)射擊精度的影響。

基于模態(tài)集成法建立身管柔性體模型。模態(tài)集成法將柔性身管看作是有限元模型的節(jié)點(diǎn)集合,其相對(duì)于局部坐標(biāo)系有小的線性變形,局部坐標(biāo)系可以有大的非線性整體平動(dòng)和轉(zhuǎn)動(dòng)。每個(gè)節(jié)點(diǎn)的線性局部運(yùn)動(dòng)近似為模態(tài)振型或模態(tài)振型向量的線性疊加。本文中采用模態(tài)集成法在ANSYS/Workbench軟件中生成零部件的柔性體中性文件流程如圖2所示,圖3是基于該方法建立的身管有限元模型。模型共有115 200個(gè)節(jié)點(diǎn)、66 569個(gè)元素,建立了6個(gè)外部節(jié)點(diǎn)與自動(dòng)機(jī)機(jī)體和炮口制退器相連。

將身管底部、前支撐面等部位固定,分析身管在約束條件下的模態(tài),部分頻率的下振型如圖4—圖6所示。各階模態(tài)信息如表1所示。

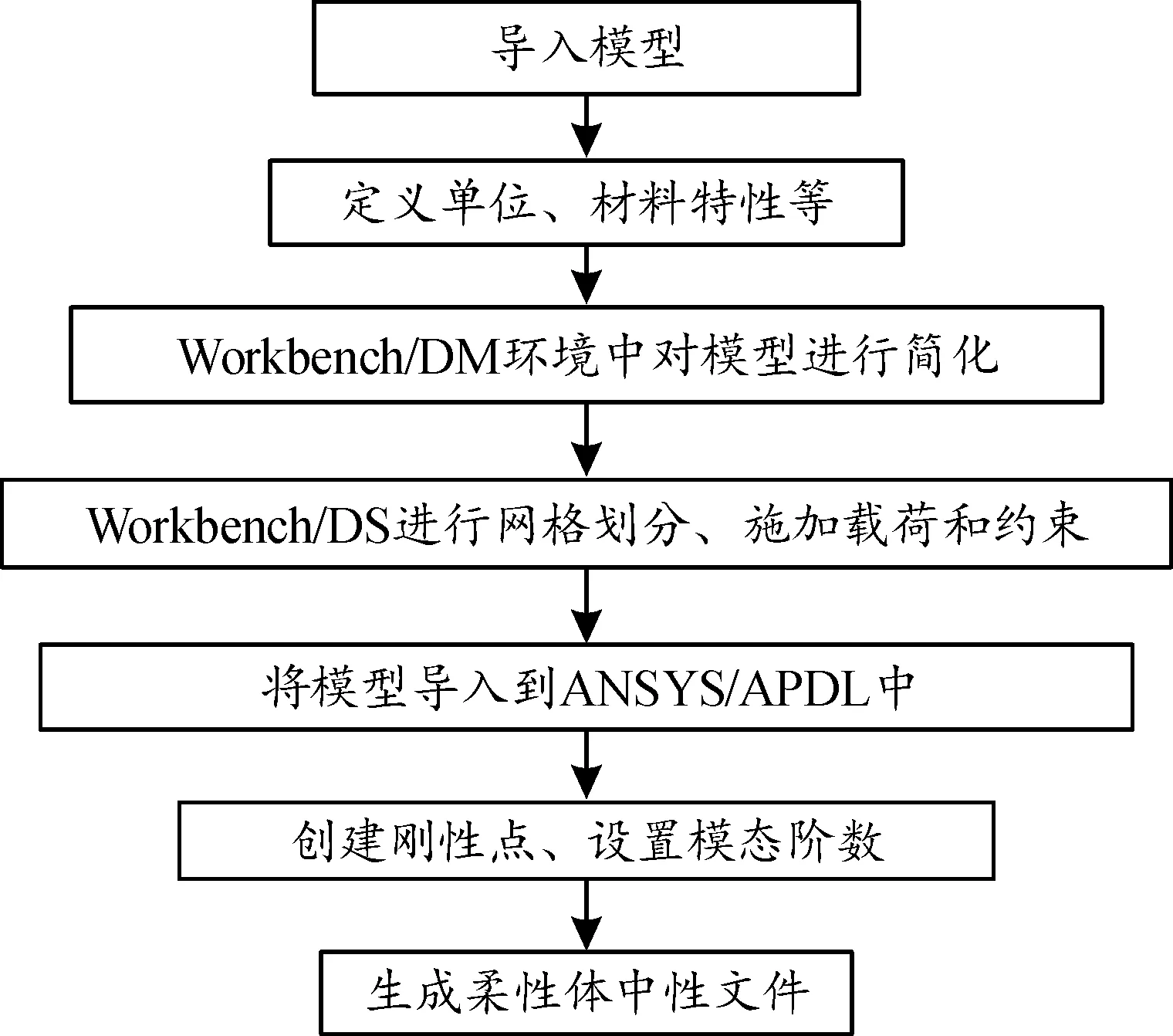
圖2 運(yùn)用ANSYS生成MNF文件流程圖

圖3 身管有限元模型

圖4 第1階模態(tài)振型

圖5 第4階模態(tài)振型

圖6 第8階模態(tài)振型

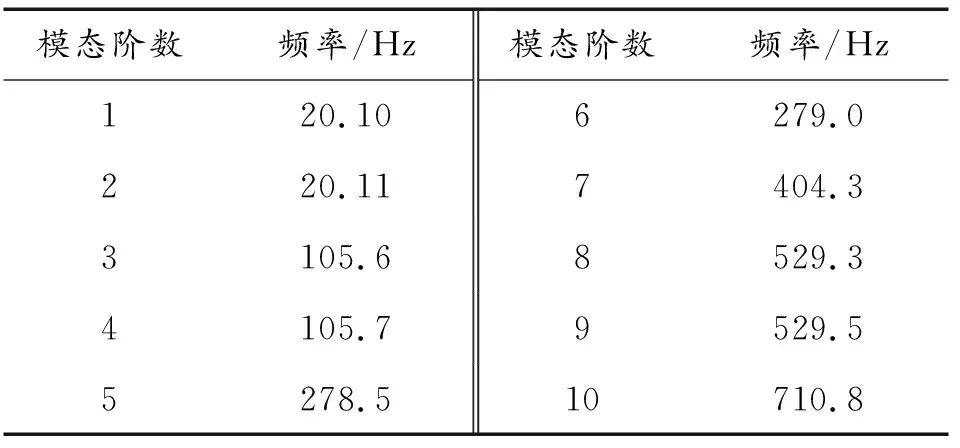
表1 身管前10階模態(tài)信息

將建立的自動(dòng)炮系統(tǒng)三維實(shí)體模型和身管柔性體模型導(dǎo)入動(dòng)力學(xué)軟件中,為各剛體零部件設(shè)定所用的材料屬性,使其自動(dòng)獲得質(zhì)量和轉(zhuǎn)動(dòng)慣量等物理信息,也可使用各零部件質(zhì)量和轉(zhuǎn)動(dòng)慣量的測試數(shù)據(jù),直接定義其物理屬性;根據(jù)圖1的系統(tǒng)動(dòng)力學(xué)拓?fù)浣Y(jié)構(gòu),定義零部件之間的運(yùn)動(dòng)副和運(yùn)動(dòng)約束。關(guān)于載荷的定義如下:

1) 自動(dòng)機(jī)受到的炮膛合力通過內(nèi)彈道計(jì)算得到的離散數(shù)據(jù)點(diǎn),將離散數(shù)據(jù)擬合成樣條曲線,以力的形式添加到自動(dòng)炮后坐部分上(自動(dòng)機(jī)機(jī)體尾部)。彈丸受到的彈底合力也采用同樣的方法施加。

2) 在自動(dòng)炮后坐部分和搖架之間添加螺旋彈簧(圖7所示),設(shè)置剛度為800 N/mm,彈簧預(yù)壓力為28 400 N,后坐阻尼系數(shù)40 N·s/mm,復(fù)進(jìn)阻尼系數(shù)1.4 N·s/mm。

圖7 緩沖彈簧添加位置

最后,根據(jù)實(shí)體模型與約束載荷等參數(shù)建立自動(dòng)炮動(dòng)力學(xué)特性仿真模型,如圖8所示。

圖8 自動(dòng)炮發(fā)射動(dòng)力學(xué)特性仿真模型

1.3 模型的驗(yàn)證

自動(dòng)炮動(dòng)力學(xué)仿真步長設(shè)置為一個(gè)射擊循環(huán),在實(shí)際射擊過程中,后坐力是一個(gè)非常重要的參數(shù),后坐力直接影響各個(gè)機(jī)構(gòu)件的運(yùn)動(dòng)行程以及射擊時(shí)傳遞的載荷大小,因此可以通過火炮水平射擊時(shí)后坐和復(fù)進(jìn)時(shí)后坐力及后坐位移曲線,來驗(yàn)證模型的準(zhǔn)確性。模型驗(yàn)證以及后續(xù)計(jì)算分析的邊界條件設(shè)定為:高低、方向射角0°,常溫穿甲彈射擊。圖9和圖10分別為后坐力和后坐位移的試驗(yàn)值和仿真值曲線。

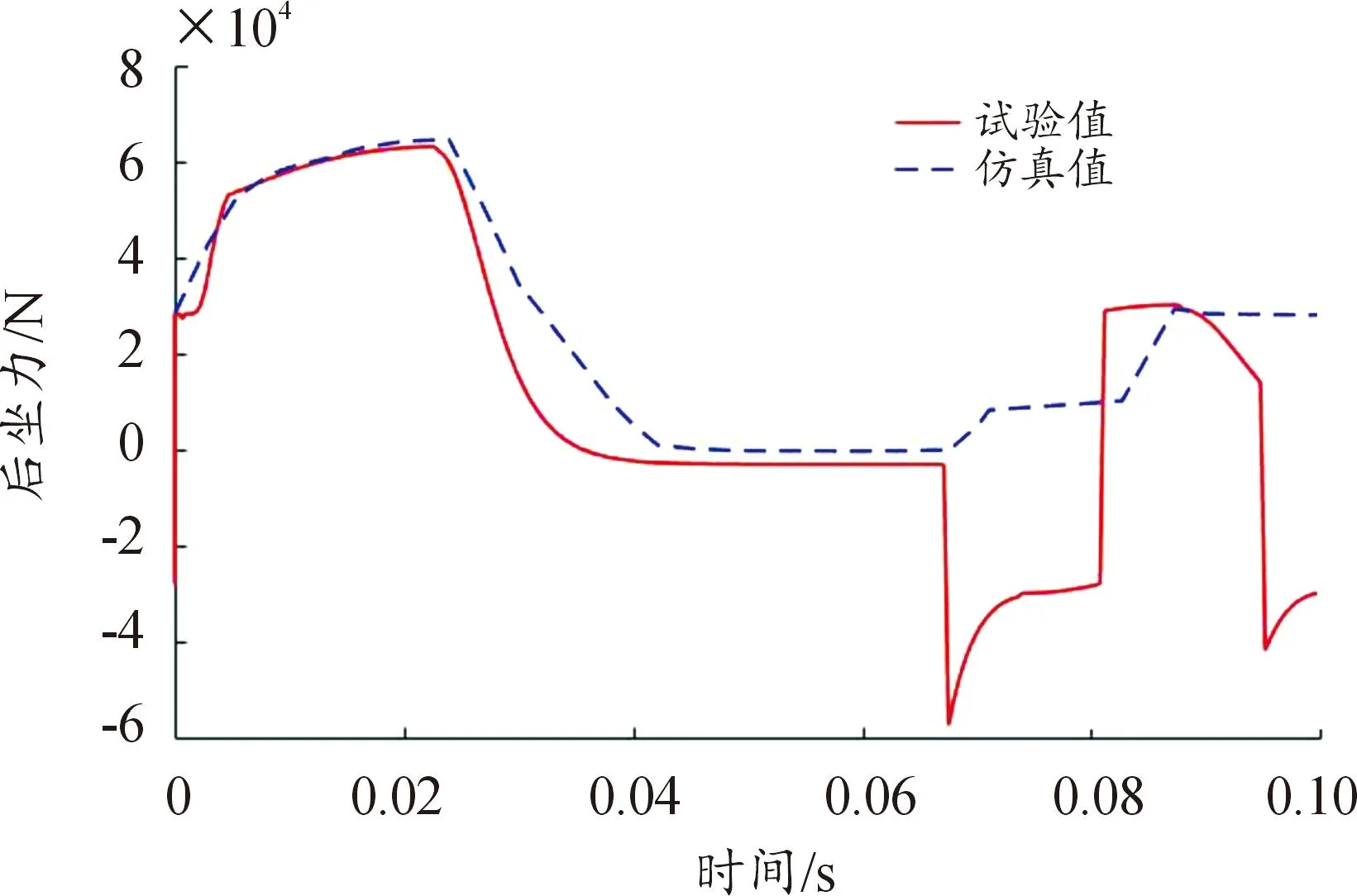
圖9 后坐力仿真值與測試值對(duì)比圖

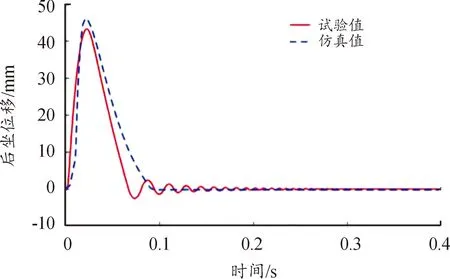
圖10 后坐位移仿真值與試驗(yàn)值曲線

經(jīng)過計(jì)算,后坐阻力相關(guān)系數(shù)89.3%,而后坐速度相關(guān)系數(shù)為87.1%,從數(shù)據(jù)上看出,后坐阻力和后坐位移曲線重合度比較高,說明自動(dòng)炮發(fā)射動(dòng)力學(xué)特性仿真模型有較高的可信度。

2 炮口振動(dòng)仿真結(jié)果

2.1 單發(fā)射擊仿真結(jié)果

對(duì)建立的自動(dòng)炮動(dòng)力學(xué)特性仿真模型進(jìn)行數(shù)值仿真計(jì)算,仿真工況為:高低射角和方向射角均為0°。下面給出彈丸出炮口瞬間及單發(fā)射擊循環(huán)周期內(nèi)的彈丸及炮口動(dòng)態(tài)特性仿真結(jié)果。

2.1.1彈丸出炮口瞬間仿真結(jié)果

彈丸出炮口瞬間仿真過程如圖11所示,由圖11可看出,擊發(fā)后4.2 ms,彈丸已到達(dá)炮口位置,這與內(nèi)彈道計(jì)算結(jié)果基本吻合。仿真結(jié)果顯示,彈丸出炮口時(shí),運(yùn)動(dòng)為位移2.59 m,速度為1 352.75 m/s,內(nèi)彈道計(jì)算結(jié)果分別為2.615 m和1 388.8 m/s,兩者計(jì)算結(jié)果基本一致。另外,從仿真結(jié)果可知:本文中計(jì)算的自動(dòng)炮為滑膛炮,彈丸出炮口的速度很高,彈丸質(zhì)心在高低向和方位向的振動(dòng)位移、速度及角位移、角速度等物理量都很小,此處不再給出仿真數(shù)據(jù)。

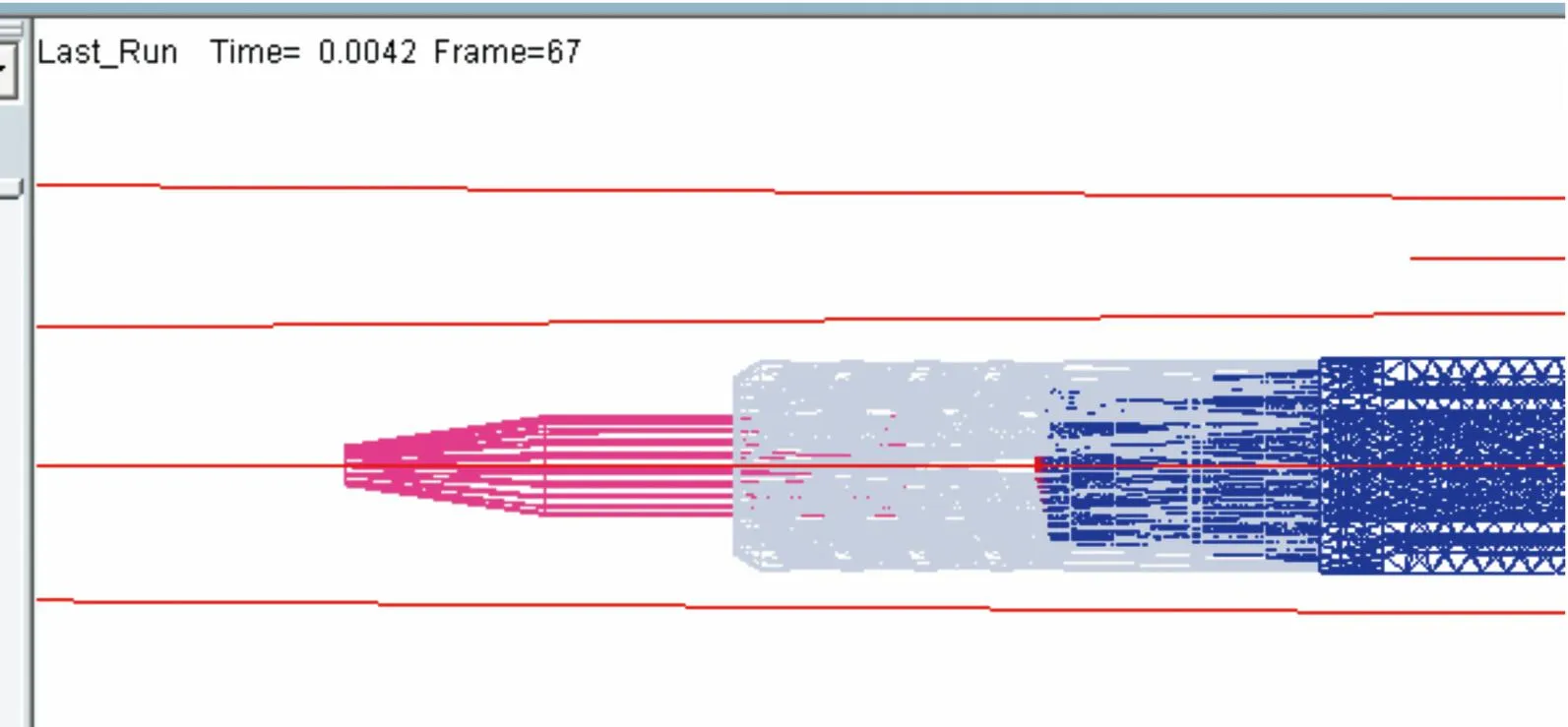
圖11 彈丸出炮口瞬間仿真過程

炮口高低向及方位向振動(dòng)位移曲線如圖12所示,炮口高低向及方位向振動(dòng)速度曲、線度曲線如圖13所示,炮口高低向及方位向振動(dòng)角速度曲線如圖14所示。設(shè)置炮口擾動(dòng)參數(shù):彈丸出炮口瞬間,炮口高低向和方位向的振動(dòng)位移分別為0.106 7 mm和-0.113 4 mm,振動(dòng)速度分別為-332.7 mm/s和-21.25 mm/s,振動(dòng)角速度分別為46.79 deg/s和-179.98 deg/s。根據(jù)炮口擾動(dòng)參數(shù),可估算出彈丸的落點(diǎn)偏差,從而計(jì)算火炮射擊密集度。

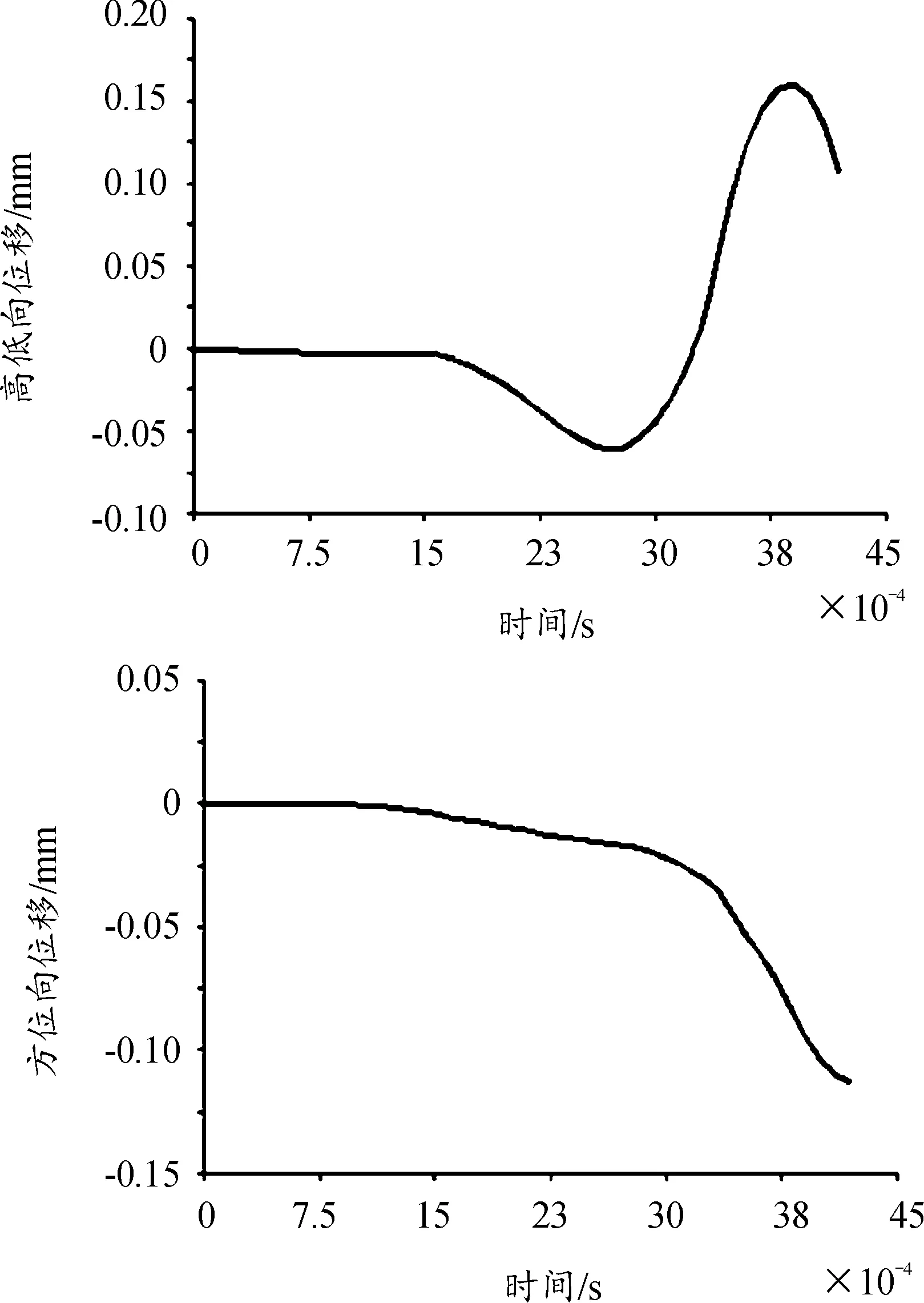
圖12 炮口高低向及方位向振動(dòng)位移曲線

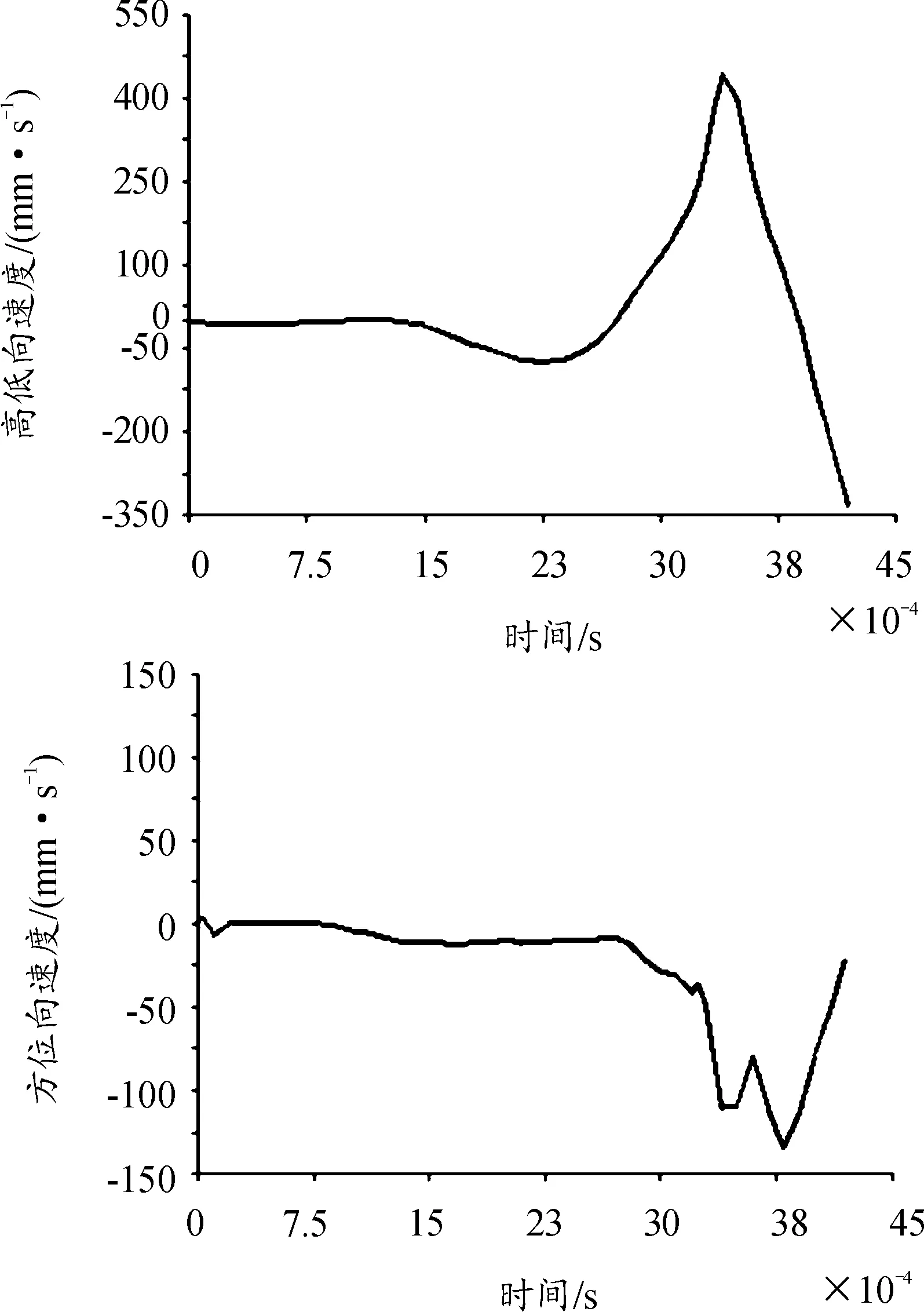
圖13 炮口高低向及方位向振動(dòng)速度曲線

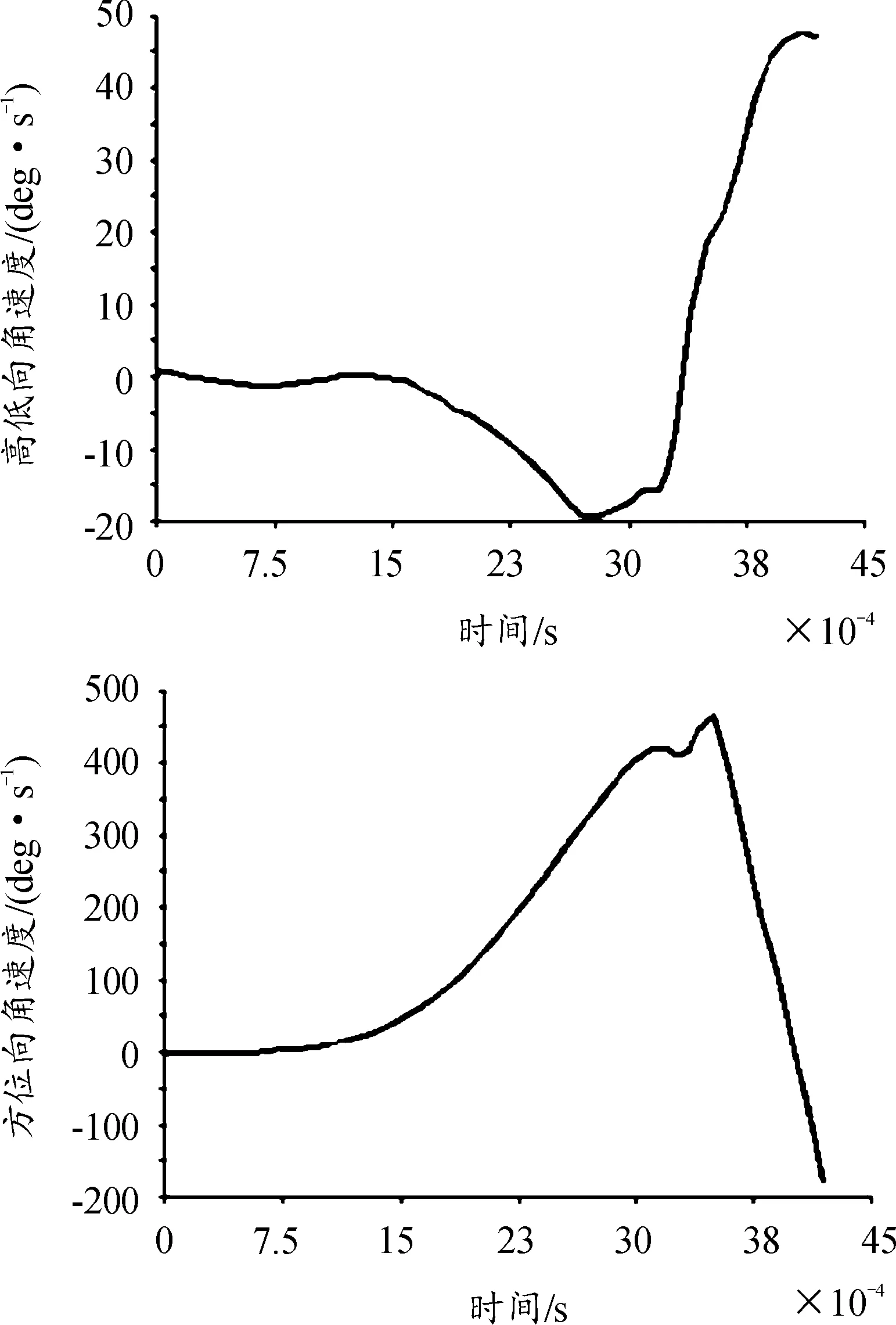
圖14 炮口高低向及方位向振動(dòng)角速度曲線

2.1.2單發(fā)射擊循環(huán)周期內(nèi)炮口振動(dòng)仿真結(jié)果

炮口高低向及方位向振動(dòng)位移曲線和振動(dòng)速度曲線分別如圖15、圖16所示。

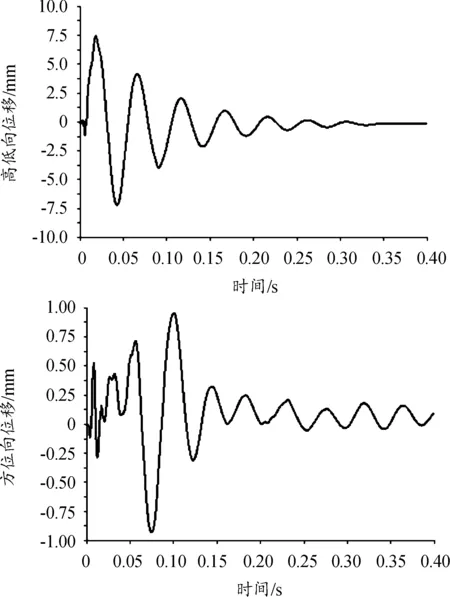
圖15 炮口高低向及方位向振動(dòng)位移曲線

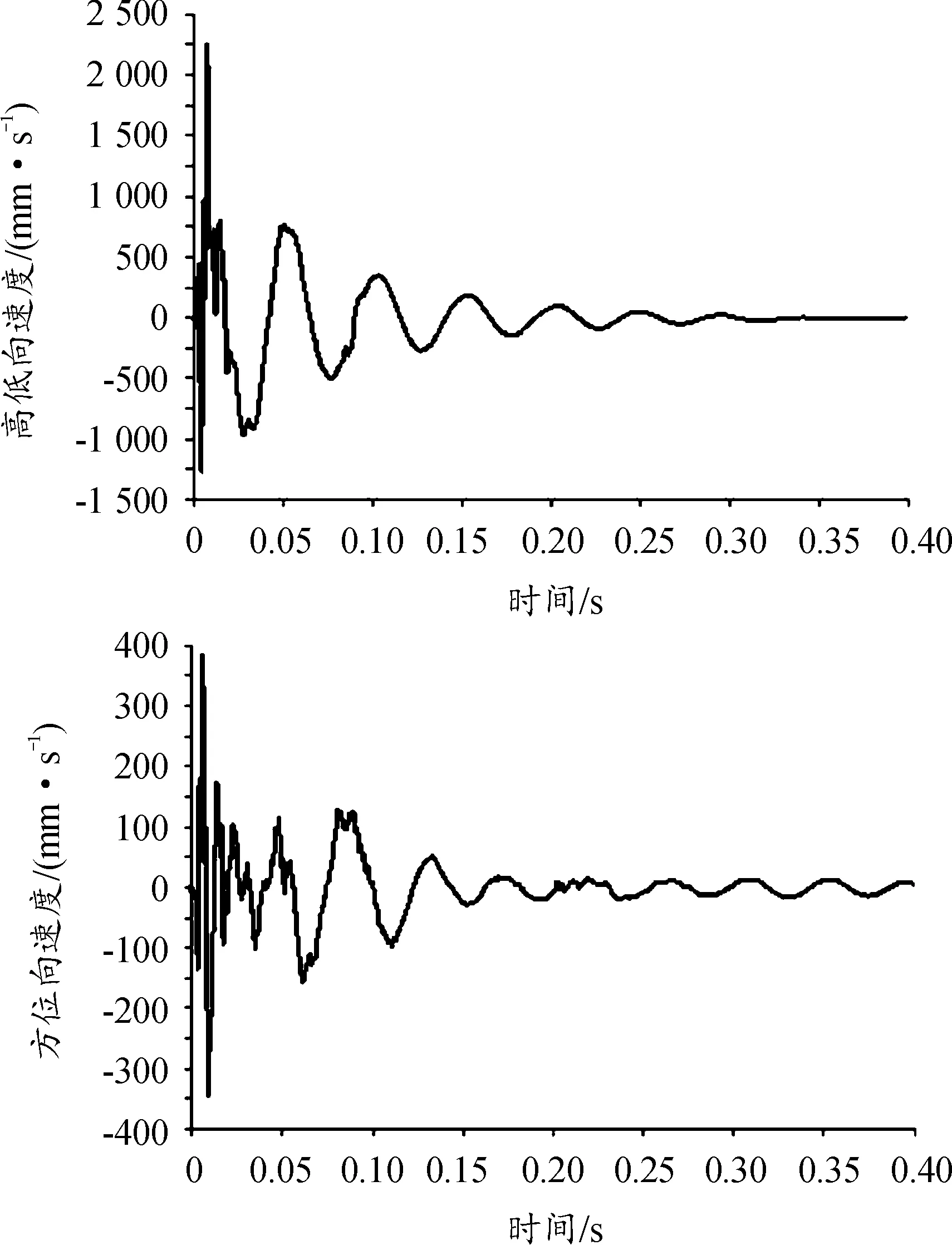
圖16 炮口高低向及方位向振動(dòng)速度曲線

從圖15、圖16可知:在一個(gè)射擊周期內(nèi),炮口高低向的振幅和振動(dòng)速度大于方位向,但高低向振動(dòng)在下一個(gè)射擊周期開始前能趨于穩(wěn)定,方位向的振動(dòng)在下一個(gè)射擊周期開始前沒有完全恢復(fù),前一發(fā)彈的射擊對(duì)下一發(fā)彈產(chǎn)生一定的影響。

2.2 連發(fā)射擊仿真結(jié)果

對(duì)上述自動(dòng)炮動(dòng)力學(xué)特性仿真模型進(jìn)行連發(fā)射擊數(shù)值仿真計(jì)算,仿真工況為:高低射角和方向射角為0°,射頻為150 rounds/min,5連發(fā)穿甲彈射擊,仿真時(shí)采用變步長方法,各發(fā)彈丸內(nèi)彈道時(shí)期,取計(jì)算步長為0.000 1 s,其他時(shí)期步長為0.01 s。

圖17—圖22為5連發(fā)射擊過程中,炮口高低向和方位向振動(dòng)特性圖。

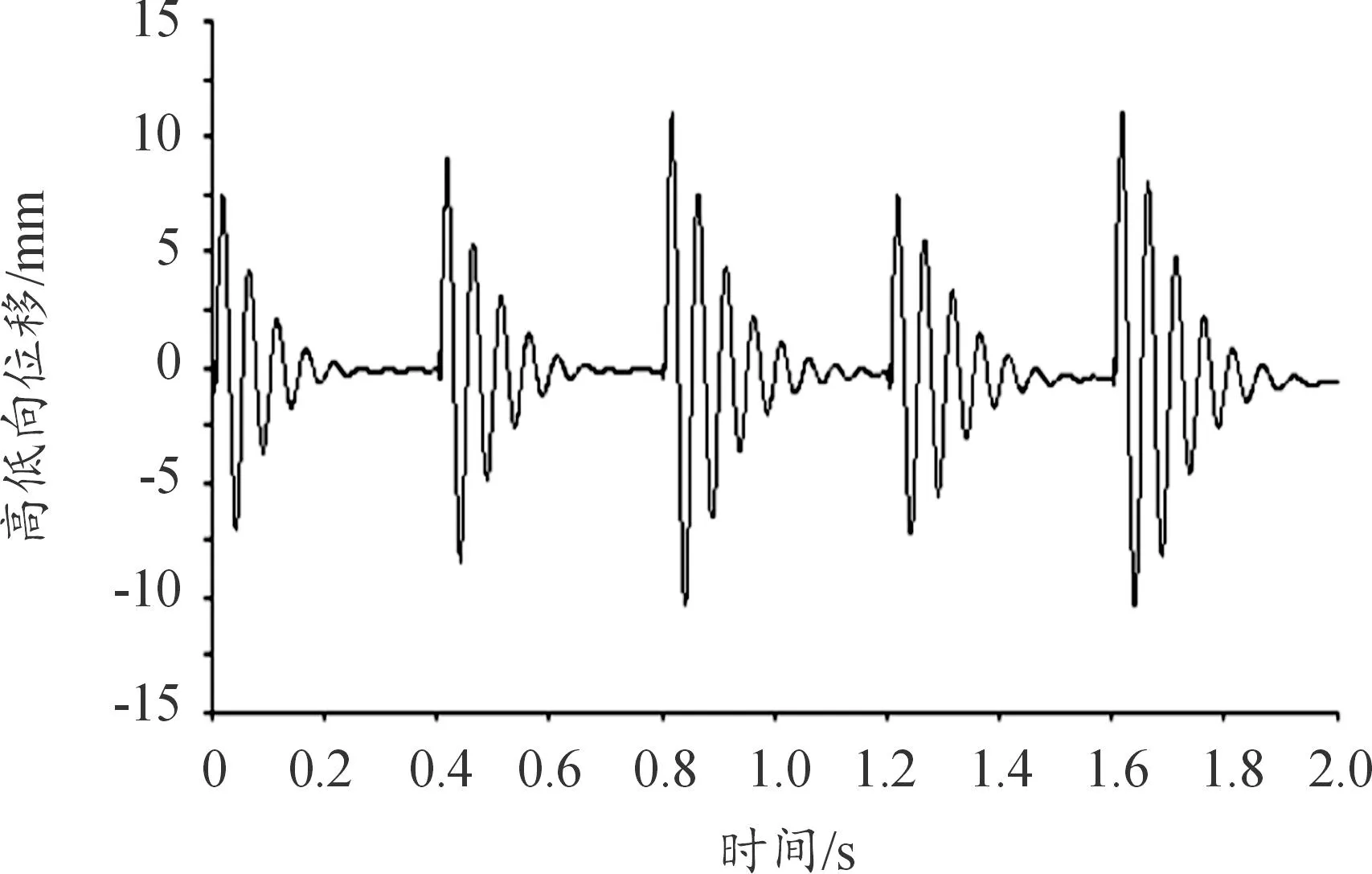
圖17 炮口中心點(diǎn)高低向振動(dòng)位移曲線

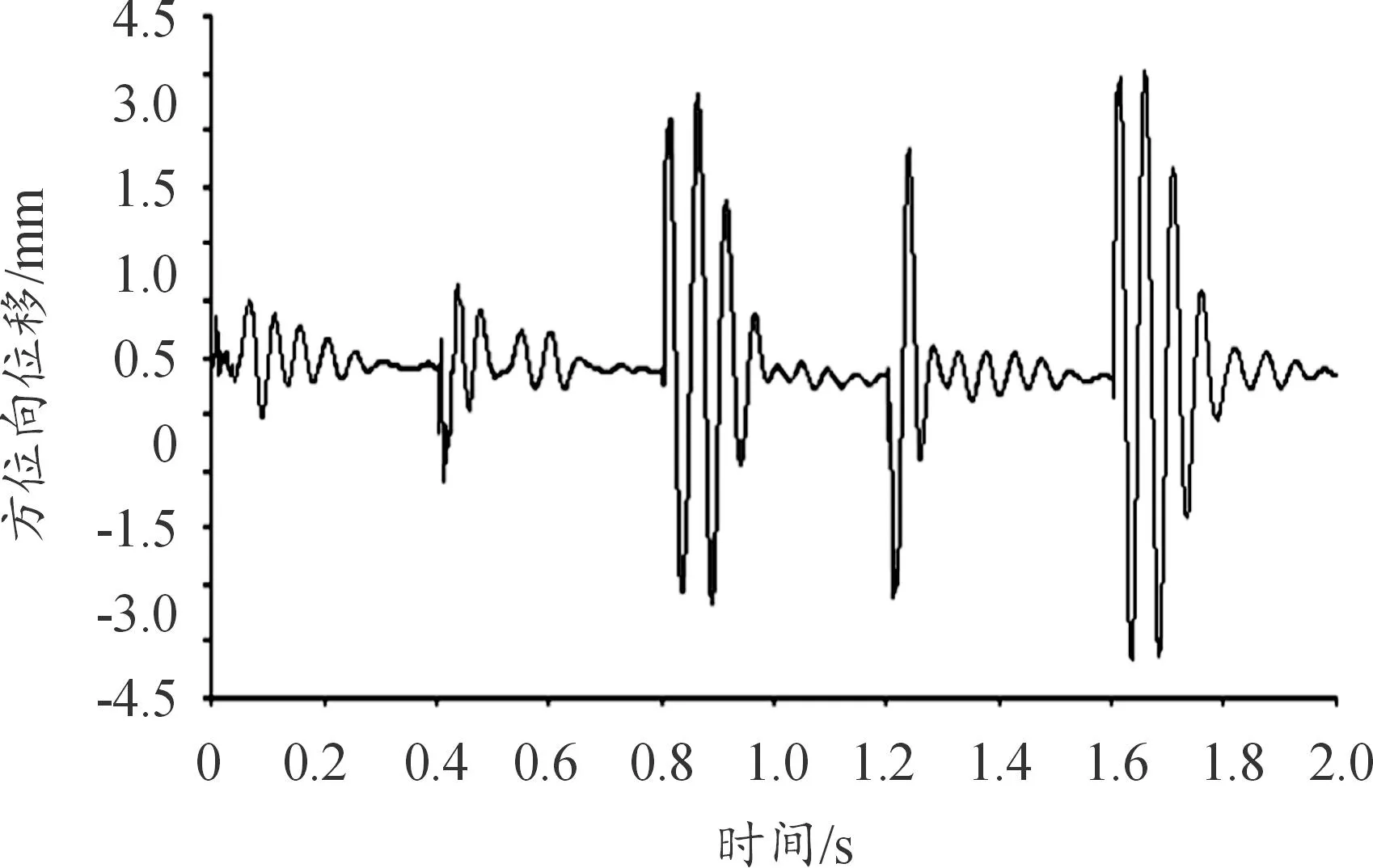
圖18 炮口中心點(diǎn)方位向振動(dòng)位移曲線

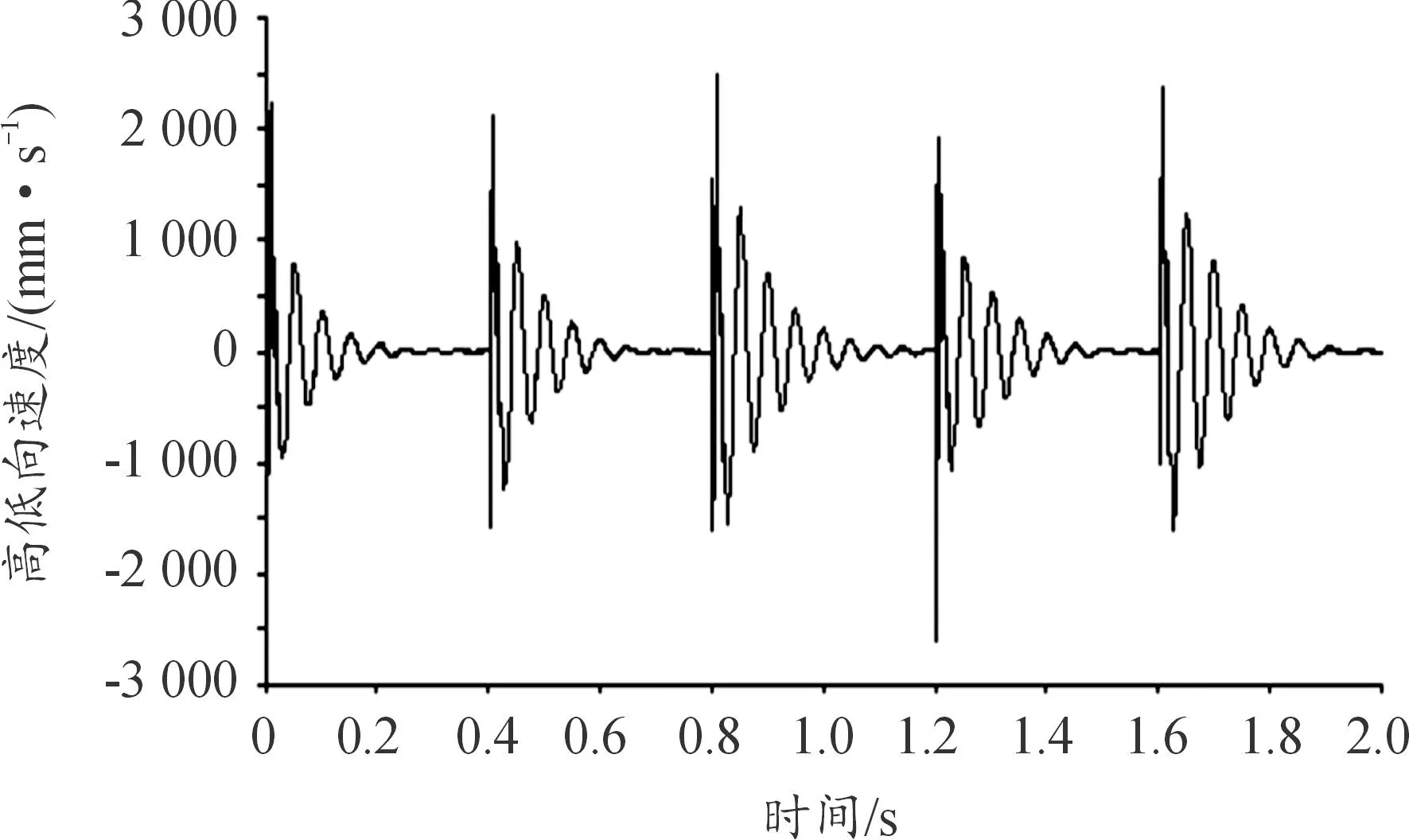
圖19 炮口中心點(diǎn)高低向振動(dòng)速度曲線

圖20 炮口中心點(diǎn)方位向振動(dòng)速度曲線

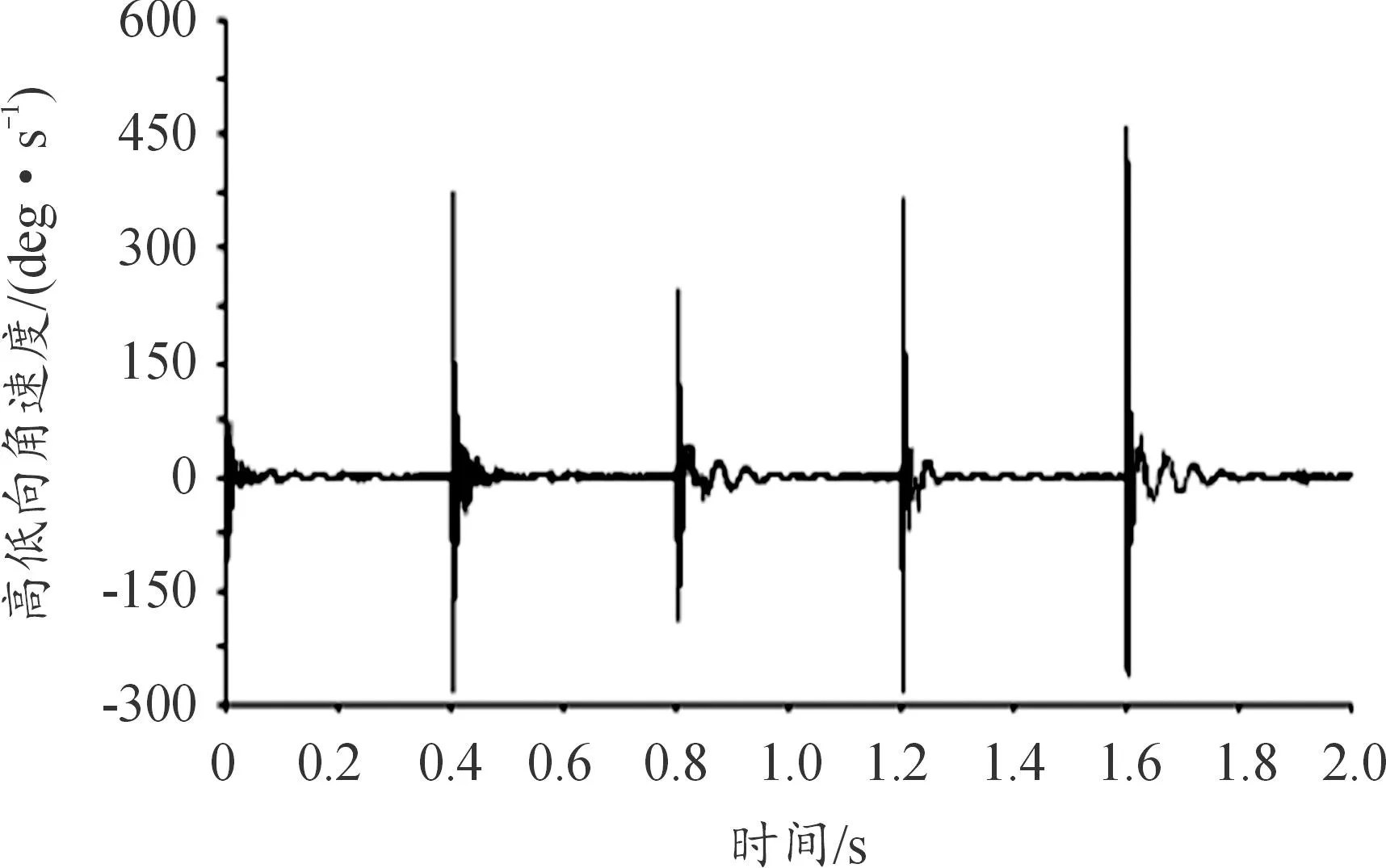
圖21 炮口中心點(diǎn)高低向振動(dòng)角速度曲線

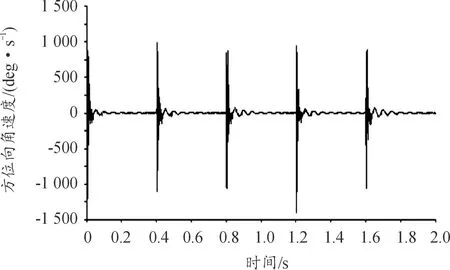
圖22 炮口中心點(diǎn)方位向振動(dòng)角速度曲線

由圖17—圖22可看出:連發(fā)射擊時(shí),前一發(fā)彈丸射擊后炮口中心點(diǎn)高低向和方位振動(dòng)在下一發(fā)彈丸射擊時(shí)沒有完全恢復(fù)初始狀態(tài),身管振動(dòng)將產(chǎn)生疊加現(xiàn)象,對(duì)下一發(fā)彈的射擊將產(chǎn)生影響。從圖17和圖18可看出,炮口高低向和方位向的最大振幅較前一發(fā)彈射擊時(shí)都有一些增加,特別是在方位向比較明顯,第3發(fā)彈擊發(fā)后的炮口最大振幅較前2發(fā)彈射擊時(shí)有明顯的增加;在高低向,隨著射彈發(fā)數(shù)的增加,炮口點(diǎn)的位置向下偏移。因此,設(shè)計(jì)時(shí)應(yīng)盡量使身管振動(dòng)在下一發(fā)彈丸射擊時(shí)恢復(fù)到最小,保持各發(fā)彈丸射擊的一致性,提高射擊密集度。

3 臺(tái)架射擊密集度計(jì)算

自動(dòng)炮通常用于近距離直瞄射擊,立靶密集度是其重要的戰(zhàn)技指標(biāo)之一[14]。根據(jù)彈道學(xué)理論,在忽略初速偏差和橫風(fēng)等次要因素后,近距離立靶散布的主要影響因素是跳角[15]。

跳角是指彈丸底部(或前定心部)脫離炮口瞬間彈丸速度矢量方向與火炮完成發(fā)射準(zhǔn)備后炮膛軸線(瞄準(zhǔn)線)的夾角,它分為起始跳角和動(dòng)力跳角,前者是由自重、加工誤差、受熱不對(duì)稱等非振動(dòng)因素引起的身管彎曲造成,而后者是由射擊載荷激發(fā)的振動(dòng)因素引起[16]。筆者主要討論與炮口振動(dòng)有關(guān)的動(dòng)力跳角。動(dòng)力跳角的高低分量為高低跳角,方向分量為方向跳角

影響動(dòng)力跳角的主要炮口振動(dòng)參數(shù)為彈丸出炮口瞬間的振動(dòng)角位移和振動(dòng)線速度。立靶散布模型為:

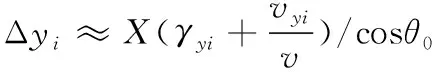
(1)

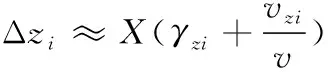
(2)

式(1)—式(2)中:Δyi、Δzi分別為高低和方位向的散布誤差;X為立靶距離;γyi、γzi分別為彈丸出炮口時(shí)的高低和方位向振動(dòng)角位移;vyi、vzi分別為高低和方位向的振動(dòng)線速度;彈丸速度矢量v是彈丸出炮口時(shí)彈丸沿炮口法線方向的線速度;θ0為射角。

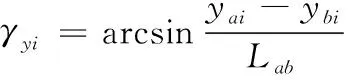
(3)

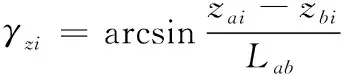
(4)

式(3)—式(4)中:yai、ybi分別高低向測量點(diǎn)a、b處的振動(dòng)位移;zai、zbi為方位向測量點(diǎn)a、b處的振動(dòng)位移;Lab為測量點(diǎn)a、b的距離。

根據(jù)以上立靶散布模型估算該自動(dòng)炮千米立靶散布精度。本文中計(jì)算的射擊工況為:0°射角,10連發(fā)穿甲彈射擊,立靶距離為1 000 m。動(dòng)力學(xué)仿真時(shí),記錄炮口附近相距300 mm的2個(gè)點(diǎn)在每發(fā)彈丸出炮口瞬間的高低向和方位向位移。

根據(jù)炮口振動(dòng)特性仿真結(jié)果及統(tǒng)計(jì)的十連發(fā)數(shù)據(jù),計(jì)算得到十發(fā)彈丸的散布誤差如表2所示。

根據(jù)表2中的數(shù)據(jù),并通過式(5)計(jì)算表示立靶密集度的高低中間誤差和方向中間誤差,計(jì)算得到該自動(dòng)炮的千米立靶散布精度為1.368 mil×1.164 mil。

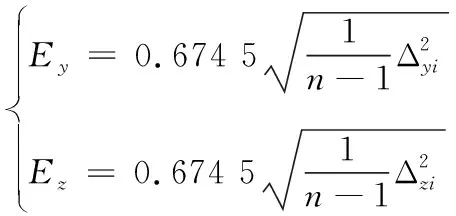
(5)

式(5)中:Ey式中為高低向密集度;Ez為方位向密集度;n為彈藥總數(shù)。

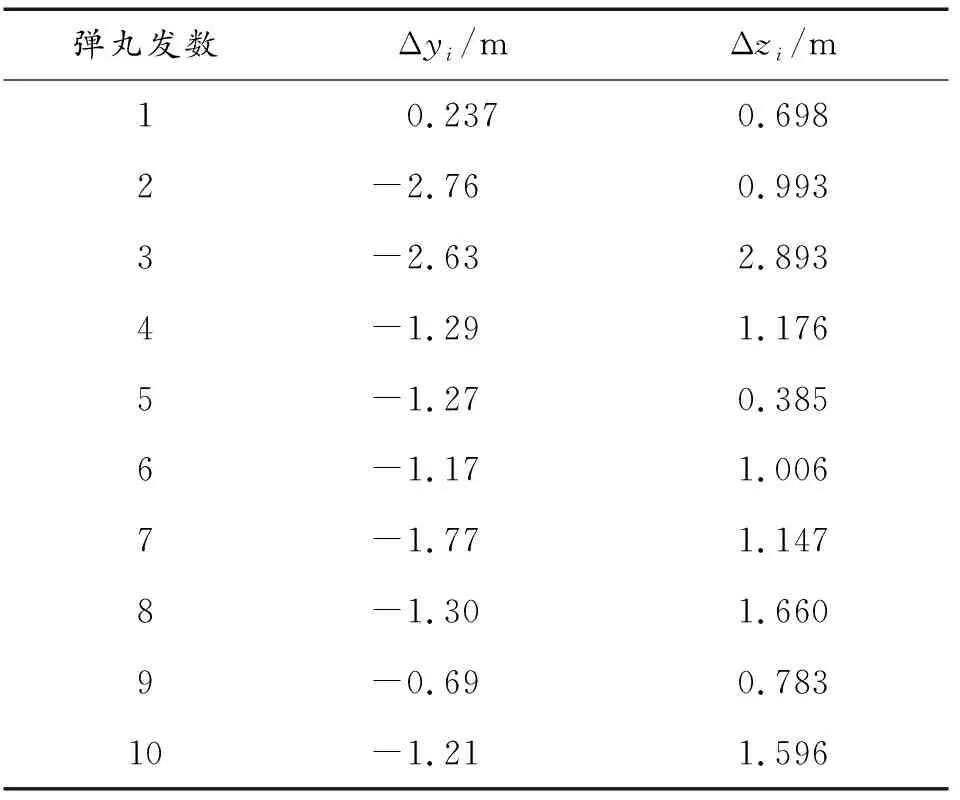
表2 各發(fā)彈丸散布誤差計(jì)算結(jié)果

從自動(dòng)炮射擊密集度計(jì)算過程可以看出,跳角分為起始跳角和動(dòng)力跳角,它是近距離立靶密集度的主要影響因素。起始跳角由身管的非振動(dòng)特性引起,一般難以控制,而動(dòng)力跳角受炮口振動(dòng)特性影響,主要包括彈丸出炮口瞬間的振動(dòng)角位移和振動(dòng)線速度。因此,在自動(dòng)炮設(shè)計(jì)過程中,可以考慮從結(jié)構(gòu)優(yōu)化層面上有效控制彈丸出炮口時(shí)的振動(dòng)特性,改善彈丸出炮口的一致性,從而提高火炮的射擊精度。

4 結(jié)論

本文中建立了某自動(dòng)炮發(fā)射動(dòng)力學(xué)特性仿真模型,仿真分析了射擊過程中炮口振動(dòng)特性及規(guī)律,并根據(jù)炮口特性數(shù)據(jù)對(duì)射擊密集度進(jìn)行初步計(jì)算。研究結(jié)果表明:

1) 該自動(dòng)炮建立的虛擬樣機(jī)模型后坐阻力和后坐位移曲線重合度比較高,模型具有較高的可信度;

2) 一個(gè)射擊周期內(nèi),炮口高低向的振幅和振動(dòng)速度大于方位向,且前一發(fā)彈的射擊對(duì)下一發(fā)彈產(chǎn)生一定的影響,連發(fā)時(shí)身管振動(dòng)將產(chǎn)生疊加現(xiàn)象;

3) 經(jīng)過估算,固定臺(tái)架上該自動(dòng)炮的射擊密集度為:1.368 mil×1.164 mil。設(shè)計(jì)時(shí)應(yīng)盡量使身管振動(dòng)在下一發(fā)彈丸射擊時(shí)恢復(fù)到最小,保持各發(fā)彈丸射擊的一致性,提高射擊密集度。

研究結(jié)果對(duì)火炮射擊精度的提高和火炮結(jié)構(gòu)優(yōu)化具有一定的參考價(jià)值。