基于螢火蟲算法和粒子群算法在產線平衡中的應用研究

聶湘萍

（廣西柳工機械股份有限公司，廣西 柳州 545007）

裝配作為生產制造的最終階段，在生產流程中起著非常關鍵的作用。裝配問題是指在一定的限制下，將多個相互關聯且相互制約的工藝節點進行有效的配置。裝配線平衡需要確保各個工位能高效、有序生產,達到減少人力和資源浪費、提高裝配效率和減少成本的目的。傳統的單產品裝配線已不能適應當下社會需求，因此，混流生產線逐漸被汽車和電子產品等制造業所采用。產線平衡（ALBP）是制造業領域中非常關鍵的研究方向，ALBP 平衡性關系到企業的生產效率、成本以及市場競爭力。Bryton 在1954 年首先對裝配線平衡問題進行了較為全面的探討。Scholl 等針對裝配線平衡問題所使用的分支定界方法，利用“局部下界”思想，提高了算法的計算效率；Mcmullen 等人利用螢火蟲算法求解多目標的產線平衡問題；彭慧等針對混合流水裝配線二級平衡問題，構建了生產節拍加權和平均負荷模型，并借助粒子群算法進行求解[1]。在現實生產中，多個度量因素都會對裝配線是否達到平衡狀態產生一定的影響，而單個指標的度量并不能精確地實現最佳平衡。基于此，螢火蟲算法和粒子群算法在產線平衡中的應用價值，根據裝配線平衡率與平滑指數來分析產線平衡。

1 裝配線平衡模型構建

產線平衡問題即在裝配線上，被處理的對象有序地沿著裝配線運行，在保證每個工件的裝配和生產優先次序的條件下，將各個工件進行適當地配置到特定數目的在線工作站，保證每個工作站的工作時長大致相同，并且不會超出生產節拍，盡量降低人員和機器的停留等情況，以達到生產目標最優化。具體研究內容為：（1）ALBP-I：在給定的生產線上得到了加工時間，并求解了極小化車間數目；（2）ALBP-II：已知流水線上的全部工位數目，并求出其最優加工時間；（3）ALBP-III：已知生產線上的機床數量，求出一種使生產線平滑指數最少的優化方案。

在平衡最優時，企業相當重視裝配線平衡率與平滑指數，平衡率愈高，整個裝配線的生產效益就愈好；此外，本項目還將重點研究裝配線的平滑指數，該指標較低說明裝配線上的各個工作站之間的負載更加平衡，從而使裝配線的總體平衡更加完美[2]。為此，本項目擬利用基于目標權重平均的優化思想，綜合考慮裝配線平衡率與平滑指數，實現裝配線的平衡度與平滑指數的有機結合，形成最優目標函數，描述如下。

1.平衡建模假設。在一條裝配線上，只能制造某種類型的一種商品；工作單元是最小的、不能重新劃分的工作單元，它的工作時間是一定的；工件可以根據工件的先后順序，將工件配置到任何一臺機床上，但任何工件都要并且只能夠被指派到確定的工作站；工件單元沒有被工作站限制，工件單元的工作時間在各個工作站之間沒有變化；在任何工作站上，其工作站工作時間均要大于產線上的生產節拍；裝配線上沒有平行工作站；裝配線上的工人技術等級沒有差別，可以在任何工作站上進行裝配；對車間閑置資源、成本等要素的沒有合理使用，忽略了工作人員在車間的行走時間。

2.目標函數。在沒有多余空閑的情況下，在裝配線上有很高的生產率，這就是最大的裝配線平衡率，表示為：

式中，N表示為裝配線上所有作業元素數量；M表示為所有工作站數量；CT表示裝配線上的生產節拍；ti表示為裝配線上i作業元素的作業時間。

在裝配線上，各工作站的工作負荷均一致，平衡性較優，即裝配線平衡指標最小化，表示為：

式中，Tk表示為裝配線上k工作站的作業時間。

目標函數F 的表達為：

約束條件為：

式中，Sa，Sb在裝配線a、b工作站上被指派的工件要素的組合；S是裝配線上各工作站上各工件單元的組合；Pij=1代表j的緊前作業元素；i∈Sk（k=1，2，…，M）代表工件i已在工作站k上進行。公式（3）是裝配線平衡度與裝配線平滑指數綜合構成的裝配線平衡最優目標方程。公式（4）代表每個工件可以被指派到一個確定的工作站；公式（5）代表工作站中全部任務單元要被分配到裝配線；公式（6）任意工作站的工作時間均要小于產線上生產節拍；公式（7）代表任務要素都要滿足任務的順序。

2 混合粒子群算法設計

當下針對產線平衡問題，可運用螢火蟲算法、粒子群算法、遺傳算法等解決。每一種算法都有著各自的特色，但是也都有著各自的缺點。1995 年，Kennedy和Eberhart 共同提出了粒子群算法，雖然粒子群算法的概念便于理解，但參數設置較多，易于實施，但是在搜索中容易出現“早熟”和容易陷入局部最優[3]。基于此，將螢火蟲算法與粒子群算法結合，以二者結合后的混合粒子群算法來求解產線平衡問題。

根據NFL 理論，任何一種算法在面對求解問題時，都會有失效的時候，但每一種算法都在各領域中具備應用價值。為此，針對產線平衡問題，功能模型復雜，“早熟”現象及粒子群算法存在的問題，故在運用粒子群算法的基礎上聯合螢火蟲算法來改善存在問題。

2.1 基本粒子群算法

粒子群算法（PSO）實質上是一種生物啟發式的迭代優化方法，它通過對兩個“極值”的比對，實現對自己搜索到的最佳點的搜索，從而獲得最優的搜索結果，從而實現對搜索結果的優化。

D 維空間內i 粒子的飛行速度和位置則為：

2.2 混合粒子群算法描述

粒子群算法在解決這一問題時具有很大的優越性，但是它依賴于初值的設置和靈敏度，且具有較低的全局尋優能力，從而降低了優化的準確性。因此，將螢火蟲算法應用于粒子群算法中，以提高其尋優能力[4]。

2.3 裝配線平衡模型與算法的映射

針對產線平衡問題中存在的一類具有離散形式的組合最優問題，傳統的H-CPSO 方法無法對其進行有效的處理，而必須對其進行適當的匹配。

1.在D 維空間內，粒子速度表示為vi=（v1，v2…vn），粒子的初始速度不定。

2.在裝配線上，每一個獨立的粒子都表示在一個裝配線的工位，xi（k）表示第i 個粒子在k 次迭代后的位置。

3.粒子的適應度函數。以產線平衡率和平滑指數為多目標平滑函數，同時將適合度功能與分配到工作站的總數量M 相對應，其表達式如下：

2.4 求解裝配線平衡模型的混合算法設計

1.種群初始化。為了保證H-CPSO 中的微粒群體產生方法的多樣化和合理性，采用了基于隨機產生的任務順序和基于位置加權的方法對群體進行了初始化，通過對各問題的隨機選擇，將權重高的問題按順序排列[5]。對粒子群產生、速率和位置進行初始化的運算如下：

2.粒子速度與位置更新。按照迭代方程，在確定了初始參數ω,c1,c2 后，可以用與這個粒子的最優位置相對應的一個隨機數目，用同樣的方法，把這個粒子的全球最優位置的隨機數字減到這個粒子的現在所在的那個隨機數字，并與c1r1 和c2r2 作積，這個計算表達式如（8）所示；在此基礎上，采用邏輯分析方法，對離子流速計算公式中的r1、r2進行了優選，計算如下：

3 計算實例

3.1 參數設定

在已有的試驗研究基礎上，從求解精度、搜索性能和計算速度三個方面，提出了一種基于遺傳算法的新型混合微粒群優化算法，參數為：種群規模m=40；慣性權重ω=0.9；學習因子c1=c2=2；初始接受概率Pr=0.8；最大迭代次數Gmax=300。

3.2 實例計算結果

工作站數量為4～9 個的6 種情況下，基本粒子群算法與混合粒子群算法裝配線作業分配方案見表1。

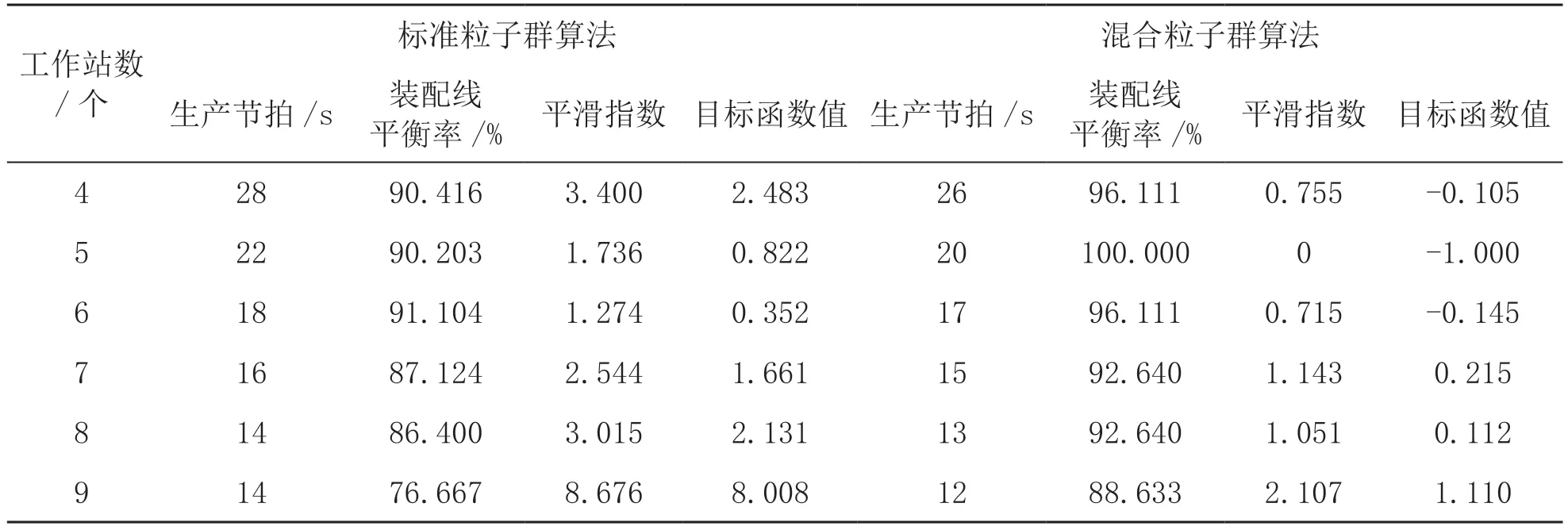
表1 MITCHELL 問題求解結果對比

實驗結果表明，不管工作站數量有多少，粒子群算法對應的目標函數值應大于混合粒子群算法對應的目標函數，因此，在產線均衡問題上，采用混合粒子群算法進行產線均衡問題的優化，并通過試驗驗證了該方法的有效性。

4 結語

本項目基于標準粒子群算法，結合多個度量裝配線運行狀態的基準參數，構建基于多個參數的裝配線平衡均衡模型。通過仿真實驗，驗證了H-CPSO 在整體搜索性能上優于傳統PSO，提高了系統的運行速度和穩定性，為裝配線平衡問題提供了更好的解決方案。