Note on: “Ballistic model for the prediction of penetration depth and residual velocity in adobe: A new interpretation of the ballistic resistance of earthen masonry”
Andreas Heine, Matthias Wickert
Fraunhofer EMI, Ernst-Zermelo-Str.4, 79104, Freiburg, Germany
Keywords: Penetration Adobe Modeling
ABSTRACT A recently published modeling approach for the penetration into adobe and previous approaches implicitly criticized are reviewed and discussed.This article contains a note on the paper titled“Ballistic model for the prediction of penetration depth and residual velocity in adobe:A new interpretation of the ballistic resistance of earthen masonry”(DOI:https://doi.org/10.1016/j.dt.2018.07.017).Reply to the Note from Li Piani et al is linked to this article.
1.Introduction
The authors of Ref.[1] suggest a model for the penetration of rigid projectiles into adobe.One of its predictions is a linear relationship between the depth of penetration in semi-infinite targets and the impact velocity,which is consistent with the experimental findings of Ref.[2].As will be shown below,the model also implies inconsistencies and predictions, which are not supported by the data.
1.1.Model evaluation
In the model of Ref.[1] it is assumed that, after an initial cratering phase at the target front side, during the main part of the penetration (tunnel region) there is a variation of the velocity v(deceleration) due to a resisting forceRwhich is directly proportional to the current penetration depthxof the projectile:
The projectile massmP, the friction coefficient μ, the target density ρT,and the projectile cross sectionAPare assumed as constants.Why there is a dependence on the gravitational accelerationgremains unclear, and the penetration process should be independent from any inclination of the shot axis with respect to the gravity field of the earth.The differential equation of Eq.(1)formally describes a harmonic oscillator and has two main implications.
Firstly, Eq.(1) implies a specific velocity-dependence of the resisting force.From the integration
it follows that
Substituting Eq.(3)into Eq.(1)shows that the effective force is:
This means that the resisting force is zero at the beginning(v =v0),and at the end of the penetration process the value of the force is.The force acting antiparallel to the direction of the penetration thus increases during the deceleration of the projectile.This reflects the fact that, as stated above, the used equations formally describe the fourth of a full period of a harmonic oscillator where, starting from zero elongation and maximum velocity, both maximum elongation and maximum acceleration appear at the turning point(zero-crossing of velocity).According to the model,the target would be loaded by the projectile like a linear spring.This is not physically consistent with the penetration processes occurring in the high-velocity impact cratering of adobe.
Secondly, as discussed in Ref.[1], the achieved penetration depthPof a spherical projectile follows as
from Eq.(3)by setting v=0 andx=P,withAP=πD2/4 andmP=ρPπD3/6, whereDand ρPare the projectile diameter and the projectile density,respectively.According to Eq.(5), the final depth of penetrationPis proportional to the impact velocity v0multiplied by the square root of the projectile diameter.This directly contradicts the data of Ref.[2],wherePwas shown to be proportional toD, thereforeP/Dbeing scale-independent.Accordingly, the predictions of Eq.(1) for spherical projectiles are not consistent with the experimentally observed phenomenology.
1.2.Application of established approaches to adobe
In view of the above it is obvious that established modeling approaches, as reviewed in Ref.[3], are more suitable also for adobe.The most promising are the R'esal equation and the widespread Poncelet form,cited here according to Ref.[4] as:
They provide as depth of penetration:
which can be approximated through Taylor expansions in the limits of αv0/β?1 and, i.e.when linear and static contribution in Eqs.(6) and (7), respectively, still dominate over the velocitysquare term.Regarding the R'esal equation, it was shown in Ref.[5] exemplarily that through the generic force law
and assumption of the drag coefficientcD(v) as v2·cD(v)=A1v+A2v2as an approximate solution
is obtainable for spherical projectiles.A second-order approximation is given in the appendix.Note that through the Poncelet form v2·cD(v) =A0+A2v2, the lowest-order approximation would already be quadratic:
The exact solutions as well as the Taylor approximations given in Eqs.(11) and (12) predict a constant ratio ofPandDat a given impact velocity, thus there is no size effect.More generically, the projectile velocity v after penetrating a distancexinto the target is dependent only on the ratio ofxandD.Specifically, the R'esal equation predicts that:
The semi-infinite penetration depth Eq.(11) depicts only the special case, where one sets v=0 andx=Pin Eq.(13).
2.Discussion
We deem the R'esal equation more suitable here, also because the static strength of adobe is small, thus negligible.The physical interpretation of this result is that - in the considered velocity regime-cavitation(inertia effects)still does not dominate and that the deceleration of the projectile is mainly due to a (linearly)velocity-dependent friction (A1≥A2v).Of course, all this still depicts a simplified model.Nonetheless,it is capable of explaining key properties of the available data [5]: By reformulating Eq.(6) as in Eq.(10),the constantsA1andA2are already independent from the projectile size (diameter of the sphere).Accordingly, the dependence of the penetration depths on impact velocityandprojectile diameter is approximately linear:
This is in contrast to the finding of Ref.[1]:
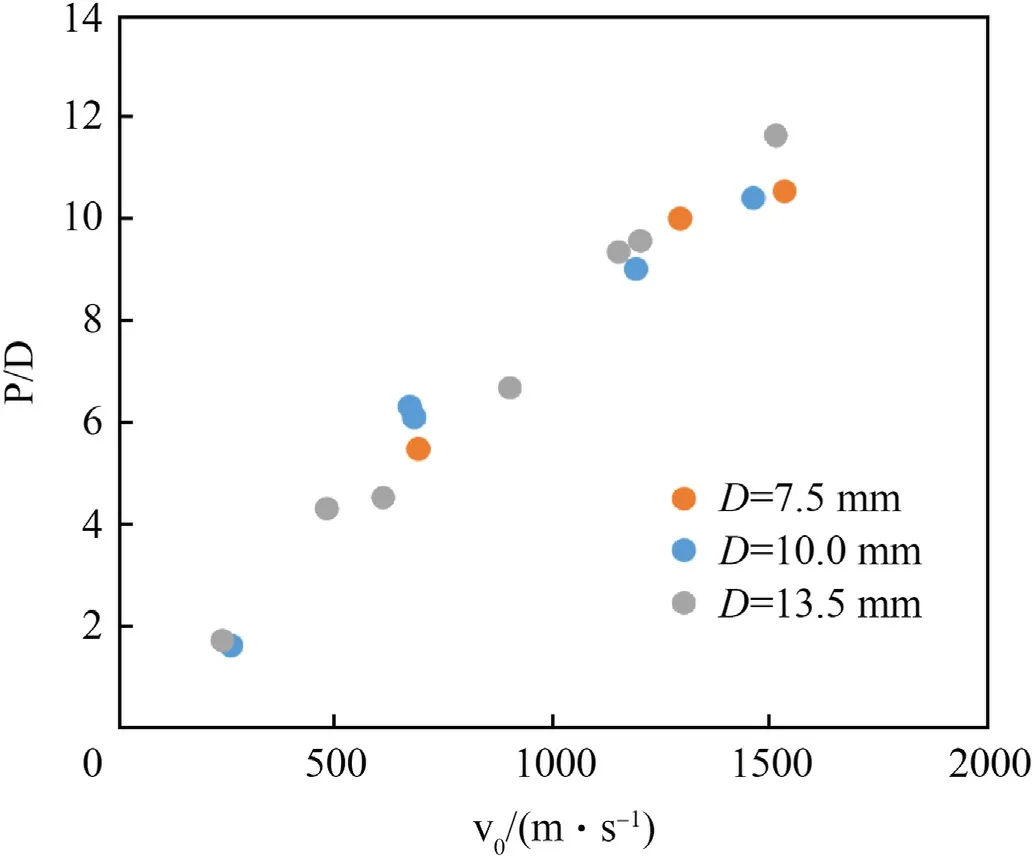
Fig.1.Data for steel spheres from Ref.[2].Only data for intact projectiles is plotted.
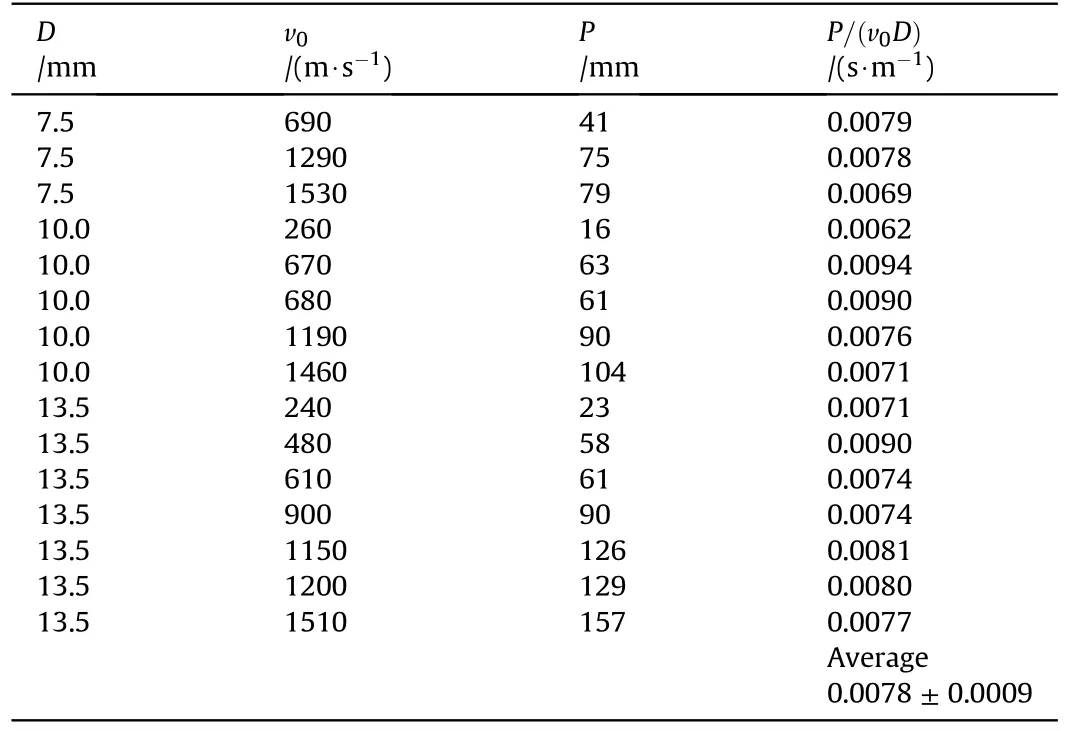
Table 1Data from Ref.[2] showing that P/(v0D)~1.Only data for intact projectiles is reported.
Independent from any modeling approach,Eq.(15),thereby Eq.(4)in Ref.[1],is not supported by the semi-infinite penetration data of Ref.[2] for steel spheres penetrating adobe of an approximate density of 1.8 g/cm3,besides that it appears to be inconsistent.This reference data is plotted in Fig.1.As shown in Table 1,the data from Ref.[2]is in good agreement with Eq.(14)and a computed constant value forP/(v0D)of(0.0078±0.0009)s·m-1,which is independent from the projectile diameter.
3.Conclusion
The alternative approach of Ref.[1] toward data and modeling considerations of Refs.[2,5] is refuted.While the theoretical interpretations given in Refs.[2,5]with the sole purpose of discussing the experimental data are simplifying but capable of reproducing key properties of the data, the alternative model of Ref.[1] even makes incorrect predictions.Accordingly,that model should not be a baseline for implicit criticism about Refs.[2,5].
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We thank BAAINBw, Koblenz, Germany for funding as well as Stefano Signetti(Fraunhofer EMI,Freiburg,Germany)for reviewing different versions of the manuscript prior to submission and for providing important comments.
Appendix
When including the second-order term of the Taylor expansion given in Eq.(11), the semi-infinite penetration depth following from the R'esal equation can be expressed as:
However,the quadratic term provides only a small correction to the linearized form for adobe[5].
- Defence Technology的其它文章
- Reply to the note by Li Piani et al.
- Book review:“Impact Engineering:Fundamentals,Experiments and Nonlinear Finite Elements”By Marcilio Alves(2020)Price at Amazon: US$ 85.67.www.impactbook.org
- Remote sensing of air pollution incorporating integrated-path differential-absorption and coherent-Doppler lidar
- Micro defects formation and dynamic response analysis of steel plate of quasi-cracking area subjected to explosive load
- Experimental and numerical study on protective effect of RC blast wall against air shock wave
- Predict the evolution of mechanical property of Al-Li alloys in a marine environment

