復(fù)雜事故樹(shù)最小割集和最小徑集求解模式研究

木拉里·馬扎甫 王越 黃超

作者簡(jiǎn)介：木拉里·馬扎甫、王越，講師；黃超，副高級(jí)工程師。

DOI：10.3969/j.issn.1671-489X.2024.02.053

摘? 要? 介紹復(fù)雜事故樹(shù)進(jìn)行最小割集和最小徑集分析過(guò)程中主要問(wèn)題，提出最小割集和最小徑集相互求解方法，建立不同結(jié)構(gòu)事故樹(shù)的最小割集和最小徑集求解模式，并通過(guò)事故樹(shù)實(shí)例驗(yàn)證最小割集和最小徑集相互求解方法及模式的正確性和有效性，為實(shí)現(xiàn)復(fù)雜事故樹(shù)分析提供有效的算法支撐。

關(guān)鍵詞? 事故樹(shù)；最小割集；最小徑集；求解模式

中圖分類號(hào)：G642.0? ? 文獻(xiàn)標(biāo)識(shí)碼：B

文章編號(hào)：1671-489X（2024）02-0053-03

0? 引言

事故樹(shù)分析是礦山及其他高危行業(yè)最常用的安全分析方法，其分析過(guò)程圍繞著最小割集和最小徑集進(jìn)行結(jié)構(gòu)重要度、概率重要度、臨界重要度及頂上事件概率分析計(jì)算，最終確定最危險(xiǎn)事故途徑和最佳控制方案[1]。因此，進(jìn)行事故樹(shù)分析必須先求出最小割集和最小徑集。但是事故樹(shù)的規(guī)模和結(jié)構(gòu)決定著最小割集和最小徑集求解的復(fù)雜程度及其數(shù)量。有些事故樹(shù)最小割集數(shù)量龐大且求解過(guò)程煩瑣，這類事故樹(shù)分析經(jīng)常只求最小徑集而不求最小割集，導(dǎo)致缺少對(duì)事故的規(guī)律性和危險(xiǎn)性的分析。有些事故樹(shù)求解最小徑集的工作量大，需要多次轉(zhuǎn)換邏輯門(mén)且畫(huà)出與原事故樹(shù)規(guī)模等同的成功樹(shù)，耗時(shí)且容易出錯(cuò)。若不求解最小徑集就不能正確分析控制事故的方案。針對(duì)此問(wèn)題，本文首先提出最小割集和最小徑集相互求解的方法，在此基礎(chǔ)上建立了不同結(jié)構(gòu)事故樹(shù)的最小割集和最小徑集的求解模式，并通過(guò)實(shí)例驗(yàn)證了該方法的正確性和有效性。

1? 通過(guò)最小割集求解最小徑集

1.1? 通過(guò)最小割集求解最小徑集的原理

最小徑集傳統(tǒng)求解方法首先需要把限制門(mén)、條件與門(mén)、條件或門(mén)等帶條件的邏輯門(mén)轉(zhuǎn)換成與門(mén)或者是與門(mén)和或門(mén)的組合，使事故樹(shù)中只有與門(mén)和或門(mén)[2]。再畫(huà)出與原事故樹(shù)規(guī)模等同的成功樹(shù)，目的就是寫(xiě)出成功樹(shù)的數(shù)學(xué)表達(dá)式，對(duì)其進(jìn)行邏輯運(yùn)算，求出成功樹(shù)的最小割集，再對(duì)偶轉(zhuǎn)換成事故樹(shù)的最小徑集。求解過(guò)程工作量大，耗時(shí)且容易出錯(cuò)。

而事故樹(shù)分析中，有了事故樹(shù)就可以寫(xiě)出對(duì)應(yīng)的數(shù)學(xué)表達(dá)式，即事故樹(shù)的數(shù)學(xué)模型，并可以利用布爾代數(shù)的知識(shí)對(duì)其進(jìn)行數(shù)學(xué)的邏輯運(yùn)算，實(shí)現(xiàn)模型的簡(jiǎn)化，從而突出頂上事件和基本事件之間的邏輯關(guān)系[3]。簡(jiǎn)化后的數(shù)學(xué)模型，即最簡(jiǎn)數(shù)學(xué)表達(dá)式，表示的邏輯關(guān)系和原事故樹(shù)表示的邏輯關(guān)系是一致的，也就是說(shuō)最初的事故樹(shù)和最簡(jiǎn)數(shù)學(xué)表達(dá)式是等同的[4]。因此，把事故樹(shù)轉(zhuǎn)換成功樹(shù)的畫(huà)圖過(guò)程用事故樹(shù)的最簡(jiǎn)數(shù)學(xué)表達(dá)式進(jìn)行對(duì)偶轉(zhuǎn)換寫(xiě)出成功樹(shù)的數(shù)學(xué)表達(dá)式來(lái)代替，對(duì)其進(jìn)行簡(jiǎn)化求出成功樹(shù)的最小割集，就能求出事故樹(shù)的最小徑集。

不難發(fā)現(xiàn)，事故樹(shù)的最簡(jiǎn)數(shù)學(xué)表達(dá)式其實(shí)就是該事故樹(shù)的最小割集。而最小割集的求解是所有事故樹(shù)分析的第一個(gè)定性分析步驟，在此基礎(chǔ)上利用該方法求解最小徑集，省略了傳統(tǒng)方法轉(zhuǎn)換帶條件邏輯門(mén)、畫(huà)成功樹(shù)等容易出錯(cuò)的、復(fù)雜的分析過(guò)程。

1.2? 實(shí)例應(yīng)用

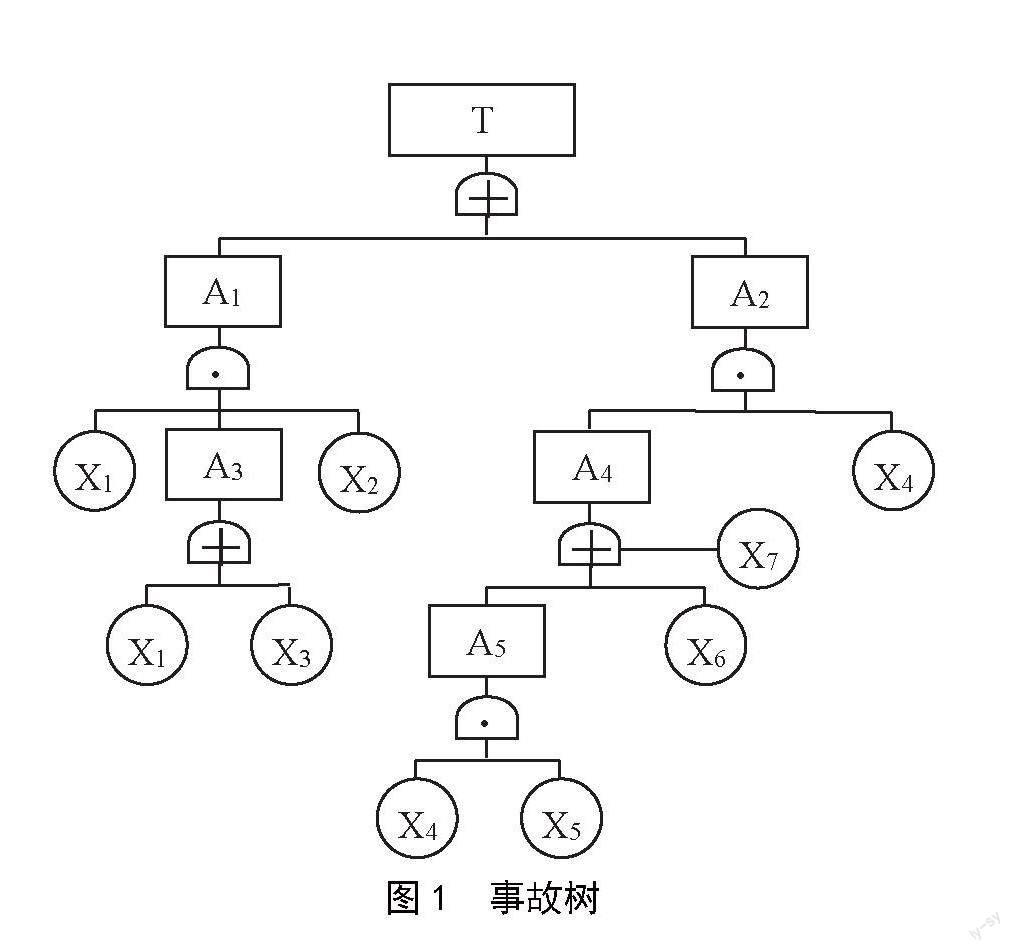
以圖1所示事故樹(shù)為例，先寫(xiě)出該事故樹(shù)的最簡(jiǎn)表達(dá)式，即最小割集。

T=A1+A2=x1x2A3+x4A4=x1x2（x1+x3）+x4x7（x6+x4x5）=x1x2+

x4x5x7+x4x6x7

事故樹(shù)最簡(jiǎn)表達(dá)式對(duì)偶轉(zhuǎn)換為成功樹(shù)的數(shù)學(xué)表達(dá)式，求解其最小割集：

則事故樹(shù)的最小徑集為：

T=（x1+x4）（x1+x7）（x1+x5+x6）（x2+x4）（x2+x7）（x2+x5+x6）

1.3? 分析

根據(jù)實(shí)例應(yīng)用可知通過(guò)最小割集求解最小徑集的方法具有以下特點(diǎn)。

1）求解最小徑集的同時(shí)，求出了最小割集，能更全面地了解事故的規(guī)律性和危險(xiǎn)性。

2）比傳統(tǒng)求解方法簡(jiǎn)單、省時(shí)，簡(jiǎn)化了轉(zhuǎn)換帶條件邏輯門(mén)的事故樹(shù)作圖和對(duì)偶轉(zhuǎn)換成功樹(shù)作圖過(guò)程，減小了手工計(jì)算的出錯(cuò)概率。尤其是對(duì)于大型復(fù)雜的事故樹(shù)，該方法更為高效。

3）因?yàn)槭鞘鹿蕵?shù)的最簡(jiǎn)數(shù)學(xué)表達(dá)式直接對(duì)偶轉(zhuǎn)換，得到的成功樹(shù)的表達(dá)式也較為簡(jiǎn)單，其簡(jiǎn)化過(guò)程，相比傳統(tǒng)求解方法中與原事故樹(shù)規(guī)模等同的、復(fù)雜的成功樹(shù)求解更為容易。

2? 通過(guò)最小徑集求解最小割集

2.1 通過(guò)最小徑集求解最小割集的原理

一般通過(guò)布爾代數(shù)對(duì)事故樹(shù)的數(shù)學(xué)表達(dá)式進(jìn)行簡(jiǎn)化求解最小割集[5]。但當(dāng)被分析的事故較危險(xiǎn)時(shí)，編制出的事故樹(shù)的規(guī)模較大，要逐步用下層事件的“與、或”組合代替上層事件，直至事故樹(shù)數(shù)學(xué)表達(dá)式中只剩基本事件，再用布爾代數(shù)對(duì)其進(jìn)行簡(jiǎn)化，這一過(guò)程非常容易出錯(cuò)。事故越危險(xiǎn)，事故樹(shù)結(jié)構(gòu)中基本事件和或門(mén)的數(shù)量越多，出現(xiàn)很多個(gè)基本事件的“與、或”組合交集的情況，導(dǎo)致簡(jiǎn)化過(guò)程煩瑣，很容易出錯(cuò)，也不能估計(jì)最小割集的數(shù)量。

在這種情況下，事故樹(shù)對(duì)應(yīng)的成功樹(shù)的結(jié)構(gòu)中與門(mén)較多，或門(mén)較少，布爾代數(shù)簡(jiǎn)化較為簡(jiǎn)單，求出的成功樹(shù)的最小割集，即事故樹(shù)的最小徑集數(shù)量較少[6]。此時(shí)，用最小徑集可以寫(xiě)出事故樹(shù)的數(shù)學(xué)表達(dá)式，其主要形式是基本事件并集的交集，它是事故樹(shù)的另外一種最簡(jiǎn)數(shù)學(xué)表達(dá)式，其邏輯關(guān)系和原事故樹(shù)的邏輯關(guān)系是一致的。對(duì)該最簡(jiǎn)數(shù)學(xué)表達(dá)式用布爾代數(shù)進(jìn)行簡(jiǎn)化，使之變成基本事件交集的并集，既是事故樹(shù)的最小割集。

2.2 實(shí)例應(yīng)用

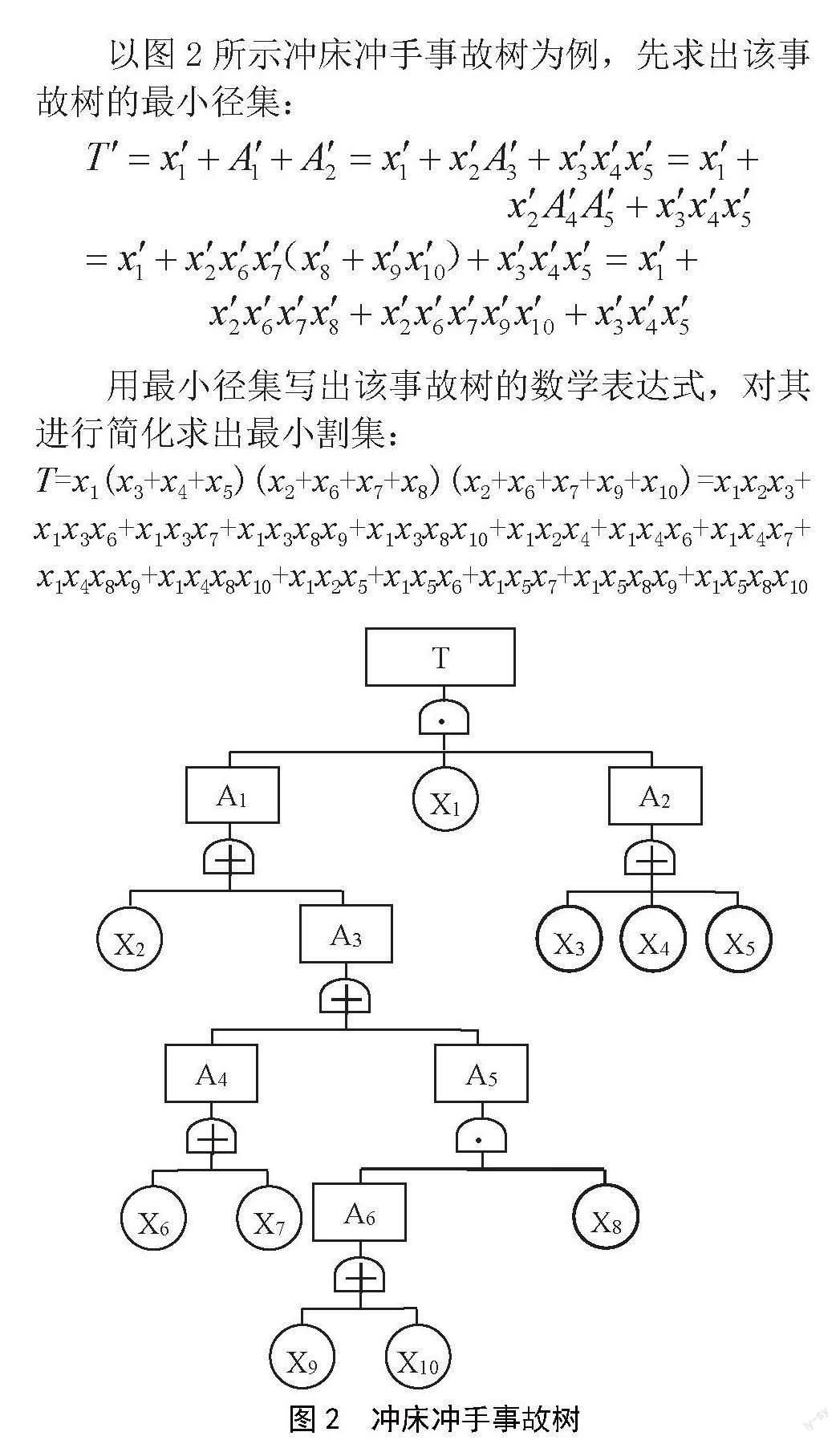
以圖2所示沖床沖手事故樹(shù)為例，先求出該事故樹(shù)的最小徑集：

用最小徑集寫(xiě)出該事故樹(shù)的數(shù)學(xué)表達(dá)式，對(duì)其進(jìn)行簡(jiǎn)化求出最小割集：

T=x1（x3+x4+x5）（x2+x6+x7+x8）（x2+x6+x7+x9+x10）=x1x2x3+

x1x3x6+x1x3x7+x1x3x8x9+x1x3x8x10+x1x2x4+x1x4x6+x1x4x7+

x1x4x8x9+x1x4x8x10+x1x2x5+x1x5x6+x1x5x7+x1x5x8x9+x1x5x8x10

2.3 分析

1）求解最小割集的同時(shí)，求出了最小徑集，能更全面地了解預(yù)防事故的方案，真正達(dá)到事故分析的目的。

2）因?yàn)樾韬?jiǎn)化的數(shù)學(xué)表達(dá)式是基本事件并集的交集，即最小徑集的邏輯乘，簡(jiǎn)化過(guò)程相比逐步用下層事件代替上層事件寫(xiě)出表達(dá)式進(jìn)行簡(jiǎn)化要簡(jiǎn)單，且不容易出錯(cuò)。

3）若對(duì)邏輯運(yùn)算熟練，可以很快算出最小割集的數(shù)量。

3? 復(fù)雜事故樹(shù)最小割集和最小徑集求解模式

以上分析證明最小割集和最小徑集是可以相互求解的，但不同的事故樹(shù)其求解難易程度大不一樣。合理的求解模式能夠高效、正確地求出最小割集和最小徑集，起到事半功倍的效果[7]。

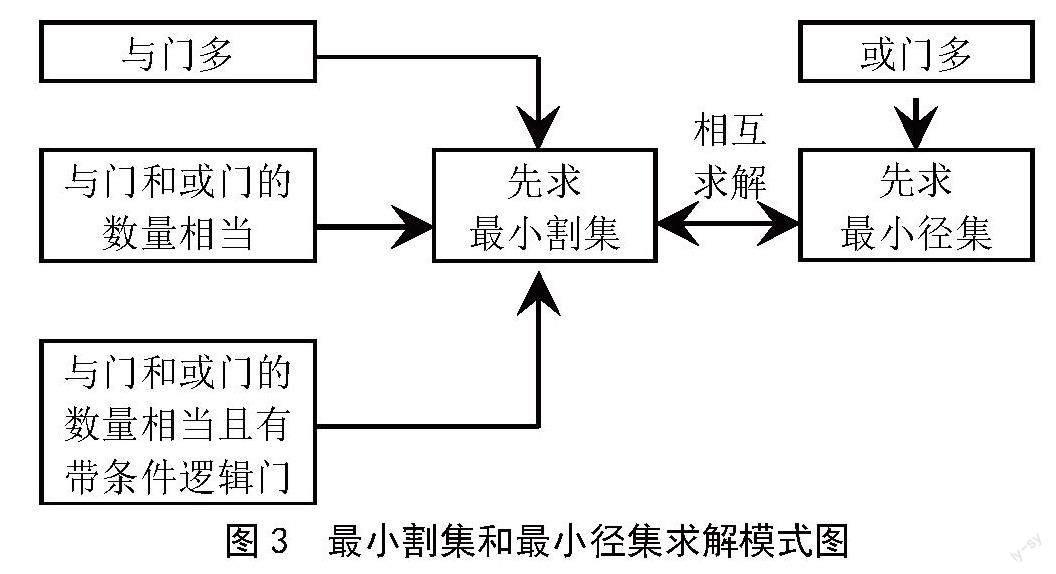
一般事故樹(shù)中或門(mén)增加最小割集的數(shù)量，與門(mén)增加最小割集的容量[8]。因?yàn)閷?duì)偶性的關(guān)系，對(duì)于最小徑集正是相反，或門(mén)增加最小徑集的容量，與門(mén)增加最小徑集的數(shù)量。根據(jù)這一規(guī)律本文提出如圖3所示的求解模式。

1）與門(mén)多。當(dāng)事故樹(shù)中與門(mén)多時(shí)，最小割集數(shù)較少，而最小徑集數(shù)較多，此時(shí)應(yīng)先求最小割集，再通過(guò)最小割集求解最小徑集。

2）或門(mén)多。當(dāng)事故樹(shù)中或門(mén)多時(shí)，最小割集數(shù)較多，而最小徑集數(shù)較少，此時(shí)應(yīng)先求最小徑集，再通過(guò)最小徑集求解最小割集。

3）或門(mén)和與門(mén)數(shù)量相當(dāng)。當(dāng)事故樹(shù)中與門(mén)和或門(mén)的數(shù)量相當(dāng)時(shí)，最小割集和最小徑集數(shù)量也相當(dāng)，但先求解最小徑集需要畫(huà)成功樹(shù)，因此該情況下應(yīng)先求最小割集，再通過(guò)最小割集求解最小徑集。

4）或門(mén)和與門(mén)數(shù)量相當(dāng)且有帶條件邏輯門(mén)。事故樹(shù)中或門(mén)和與門(mén)數(shù)量相當(dāng)且有帶條件邏輯門(mén)的情況下，先求最小割集，再通過(guò)最小割集求解最小徑集[9]。因?yàn)橛袔l件邏輯門(mén)的事故樹(shù)轉(zhuǎn)換為成功樹(shù)更為麻煩，需要先將這些帶條件邏輯門(mén)轉(zhuǎn)換為與門(mén)或者是與門(mén)和或門(mén)的組合。

4? 結(jié)束語(yǔ)

文章提出并驗(yàn)證了最小割集和最小徑集相互求解方法，該方法在最小割集的基礎(chǔ)上不畫(huà)成功樹(shù)就能求出最小徑集，在最小徑集的基礎(chǔ)上可以較為簡(jiǎn)單的求出最小割集，相比傳統(tǒng)求解方法更為簡(jiǎn)潔、高效。其次可以用該方法驗(yàn)證已經(jīng)求出的最小割集和最小徑集是否正確。在相互求解方法的基礎(chǔ)上建立了最小割集和最小徑集的求解模式，明確了不同結(jié)構(gòu)的事故樹(shù)應(yīng)該先求最小割集還是先求最小徑集，從而使事故樹(shù)分析變得更為簡(jiǎn)單。

5? 參考文獻(xiàn)

[1] 徐志勝，姜學(xué)鵬.安全系統(tǒng)工程[M].北京：機(jī)械工業(yè)出

版社，2019：110-112.

[2] 楊宏亮，黃觀明.基于故障樹(shù)最小割集的解脫器活塞斷

裂分析[J].艦船科學(xué)技術(shù)，2019，41（1）：133-137，151.

[3] 武欣，戚彬，孫曉明，等.基于模糊事故樹(shù)的農(nóng)機(jī)事故

影響因素分析[J].中國(guó)農(nóng)機(jī)化學(xué)報(bào)，2022，43（1）：211-

218.

[4] 張小浩.基于事故樹(shù)分析法的企業(yè)安全生產(chǎn)風(fēng)險(xiǎn)管理研

究[D].安徽：安徽財(cái)經(jīng)大學(xué)，2021.

[5] 耿羅通.客車(chē)制造企業(yè)安全生產(chǎn)風(fēng)險(xiǎn)分級(jí)管控模式研究

[D].北京：中國(guó)地質(zhì)大學(xué)，2020.

[6] 韓梅，吳珊，常青，等.基于事故樹(shù)和模糊貝葉斯網(wǎng)絡(luò)

的鐵路超限貨物運(yùn)輸風(fēng)險(xiǎn)評(píng)估[J].鐵道學(xué)報(bào)，2021，

43（5）：9-17.

[7] 鄒敏，王洪春.利用Petri網(wǎng)模型的求解因果圖最小割

集的算法[J].重慶師范大學(xué)學(xué)報(bào)（自然科學(xué)版），2018，

35（3）：130-136.

[8] 木拉里·馬扎甫，陸衛(wèi)東，王悅.基于最小割集求解最

小徑集的方法研究[J].煤炭技術(shù)，2017，36（8）：302-304.

[9] 代張音.煤礦復(fù)雜事故樹(shù)最小徑集算法研究[J].工業(yè)安

全與環(huán)保，2015，41（2）：44-45，61.