基于自回歸EIV模型的高鐵橋墩沉降預測方法研究

王 鵬

(中國鐵路設計集團有限公司,天津 300308)

引言

高速鐵路以其運行速度快、安全性能好、舒適度高、運輸能力大等特點,已成為當前中遠途出行的主要交通工具之一[1]。截止2022年底,我國高速鐵路運營總里程已超過4.2萬km,在建和擬建高速鐵路達數千公里,如何確保這些高鐵線路的施工建設和運營管理安全,是當前高速鐵路基礎研究的重要課題。國內外高速鐵路建設和運營維護的實踐經驗表明,要保證高速列車快速、安全、舒適運行,必須確保鐵路軌道的高平順性和高穩定性[2-3]。前者是以高精度的軌道控制網為基準,并通過軌道精調來實現;后者則要求對線下工程進行定期沉降監測和沉降控制,以此確定科學、合理的軌道板及軌道鋪設時間,并為運維方案、決策的制定提供數據支持[4-6],是前者的前提和基礎。由此可見,高速鐵路線下工程的沉降監測工作,對高速鐵路施工建設和運營管理至關重要。

橋梁是高速鐵路線下工程的重要結構形式,目前我國已建成高鐵工程中,橋梁總里程占高鐵線路總里程的50%以上,通過開展高鐵橋墩沉降測量和監測數據處理分析,及時掌握高鐵橋梁的變形情況并準確、有效預測后續可能的形變趨勢,對保障鐵路橋梁自身結構安全、線上工程穩定性、鐵路軌道平順性,進而確保高速列車行駛安全以及高速鐵路網運營安全具有重大意義[7-9]。在沉降監測數據分析的基礎上對橋墩變形趨勢進行預報,是高鐵橋墩沉降監測工作的重要環節,也是施工建設、運營維護決策制定的重要依據。目前,國內外有關沉降監測預報分析研究成果很多,有雙曲線法、指數曲線法[10]、三點法[11]等靜態預測方法,以及時間序列法[12-13]、人工神經網絡法[14]、灰色系統分析法[15]等動態預測方法。已有研究表明,受施工、運營等復雜因素影響,采用動態預測方法進行高鐵線下工程沉降預測較靜態方法更為合理。在眾多動態預測方法中,時間序列分析方法中的自回歸(AutoRegressive, AR)模型是其中最為常用的經典模型,具有理論嚴密、原理簡單、易于被測量技術人員理解和掌握等特點。將其用于高鐵橋墩沉降預報分析時,建立科學合理、符合橋墩沉降變形實際的AR模型,是保證預測結果準確、可靠的關鍵。為此,在建立顧及模型變量誤差的自回歸EIV模型基礎上,提出一種高鐵橋墩沉降預測模型選擇方法,并通過實際案例驗證了該方法的可行性和有效性。

1 基于自回歸EIV模型的高鐵橋墩沉降預報

1.1 經典AR模型

高速鐵路橋墩沉降預報分析,是基于時間序列的橋墩監測點累積沉降量進行的,對應的經典p階AR模型為

Ht=φ1Ht-1+φ2Ht-2+…+φpHt-p+εt

(1)

式中,Ht、Ht-1、…、Ht-p為同一橋墩沉降監測點(p+1)次相同時間間隔監測得到的累積沉降量;φ1、φ2、…、φp為回歸系數;εt為模型的隨機誤差;p為模型的階數。

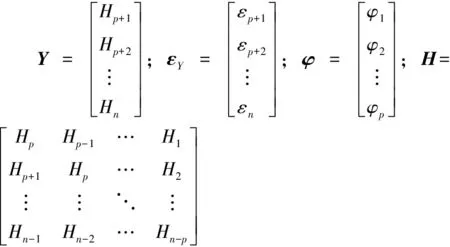
設某橋墩沉降監測點連續n期沉降監測得到的累積沉降量為H1、H2、…、Hn,則其p階自回歸模型為

Y=Hφ+εY

(2)

采用最小二乘平差方法[16],可得回歸系數估值為

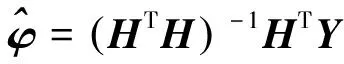
(3)

據此,可求得第n+1、n+2、n+3期橋墩沉降監測點累積沉降量預測值分別為

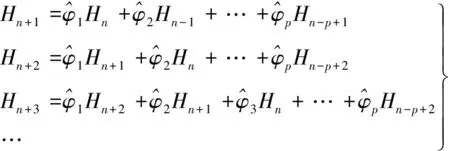
(4)

由式(1)～式(4)可以看出,p階自回歸模型的系數矩陣H由n期橋墩監測點累積沉降量組成,不可避免地會受到測量誤差的影響。因此,基于以上經典線性回歸模型,并采用最小二乘求解自回歸系數,得到的解具有偏性[17-18]。

1.2 顧及模型變量誤差的自回歸EIV模型

在經典的AR(p)模型基礎上,為模型變量引入誤差向量,式(2)可表示為

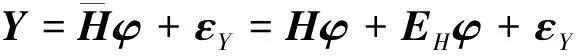
(5)

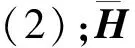
式(5)可視為非線性高斯赫爾默特模型。將EH中元素作為待估參數,有

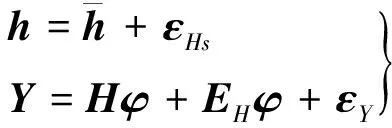
(6)

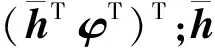
式(6)為非線性模型,將其線性化并采用高斯-牛頓法迭代求解。設第i次迭代后,參數φ的估值為φ(i),εHs的估值為εHs(i),將式(6)右端在(φ(i),εHs(i))處用泰勒級數展開并取至一階項

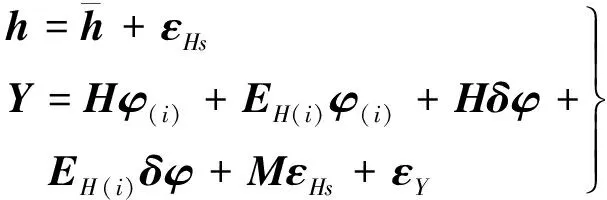
(7)

式中,δφ為φ(i)的微小改正值;M為與φ(i)及EH有關的(n-p)×(n-1)矩陣,滿足MεHs=EHφ(i)。

構造目標函數

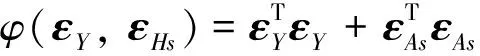
(8)

對式(8)中各變量求偏導,并令導數為0,可得

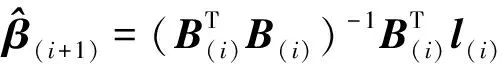
(9)

(10)

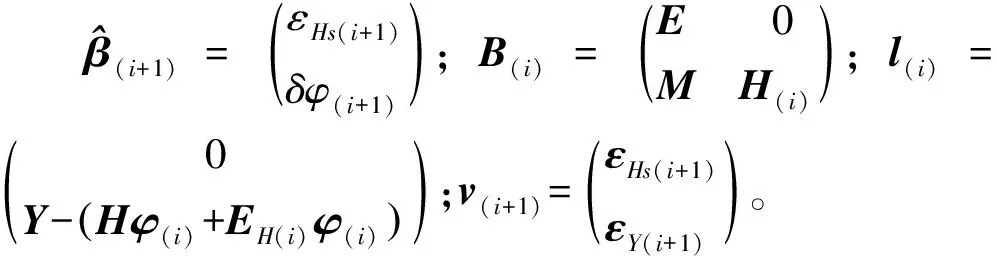
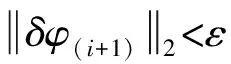
實際應用中,要建立科學合理、符合高鐵橋墩沉降實際的最佳AR模型,建模時除了要顧及模型變量誤差之外,還應選用合適的模型參數,即要合理確定模型的階數,所建模型才能準確表達橋墩沉降變形的動態特征。

2 高鐵橋墩沉降預測模型選擇

自回歸模型定階可歸結為最佳線性回歸模型的選擇問題。在眾多模型優選方法中,線性假設法是目前國內外公認的有效方法,且其原理簡單,易于測量技術人員掌握和運用。因此,在此采用線性假設法進行高鐵橋墩沉降預測模型的優選分析。

設有n期連續時間序列的橋墩沉降監測高程值。假設其自回歸模型階數為p,則式(5)即為建立的p階自回歸EIV模型。再考慮p-1階情況,其可通過在式(5)基礎上增加一個約束方程φp=0得到,即

(11)

式中,G=(0,…,0,1)為1×p向量。

以溫室內營養缽的方式來替代傳統的冷床育苗，其不僅能為幼苗的生長過程創造更加有利的環境，且能促使幼苗生長得更加健壯。與此同時，絕大多數蔬菜種類，其本身在低溫與弱光的環境下將更有助于自身生長，且同時基于高壟栽培、膜下暗灌等技術，對于病蟲害亦能起到良好的控制作用[2]。

首先,采用1.2節的方法對式(5)進行求解,設在第m次迭代后參數向量滿足收斂條件,由此可得p階自回歸EIV模型的回歸系數估值的總體最小二乘解φ(m)及觀測值殘差v(m),記殘差平方和為Sp。再對式(11)進行求解,以得到(p-1)模型的回歸系數估值的總體最小二乘解φ(m+1)、觀測值殘差v(m+1)及殘差平方和Sp-1,具體過程如下。

結合式(7),將式(11)在(φ(m),εHs(m))處采用泰勒級數展開并取至一階項,有

(12)

按求條件極值法構造目標函數

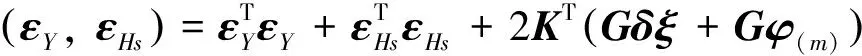
(13)

式中,K為對應約束條件的拉格朗日算子。

對各變量求偏導并令導數為0,得

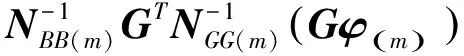
(14)

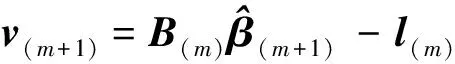
(15)

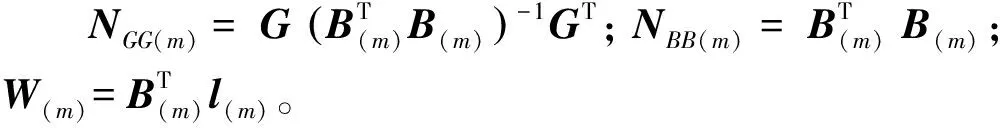
需要說明的是,預設的擬合最高階數p可首先選擇[n/3]～[2n/3]之間的整數,若在后續分析中接近預設最高階數仍未得到最佳模型,則再作調整。大量高速鐵路橋墩沉降監測工程實踐統計分析表明,其最佳自回歸EIV模型階數往往小于n/3,因此,本文預設的擬合最高階數p=n/3。

要判斷(p-1)階自回歸EIV模型是否成立,需對線性約束φp=0是否成立進行檢驗和顯著性分析。為此,提出原假設和備選假設分別為

(16)

式中,H0為原假設;H1為備選假設。當參數約束φp=0對回歸模型影響不顯著時,接受H0,p、(p-1)階模型之間無顯著差異;反之則拒絕。在H0成立時,可構造F分布的假設檢驗統計量[20],有

(17)

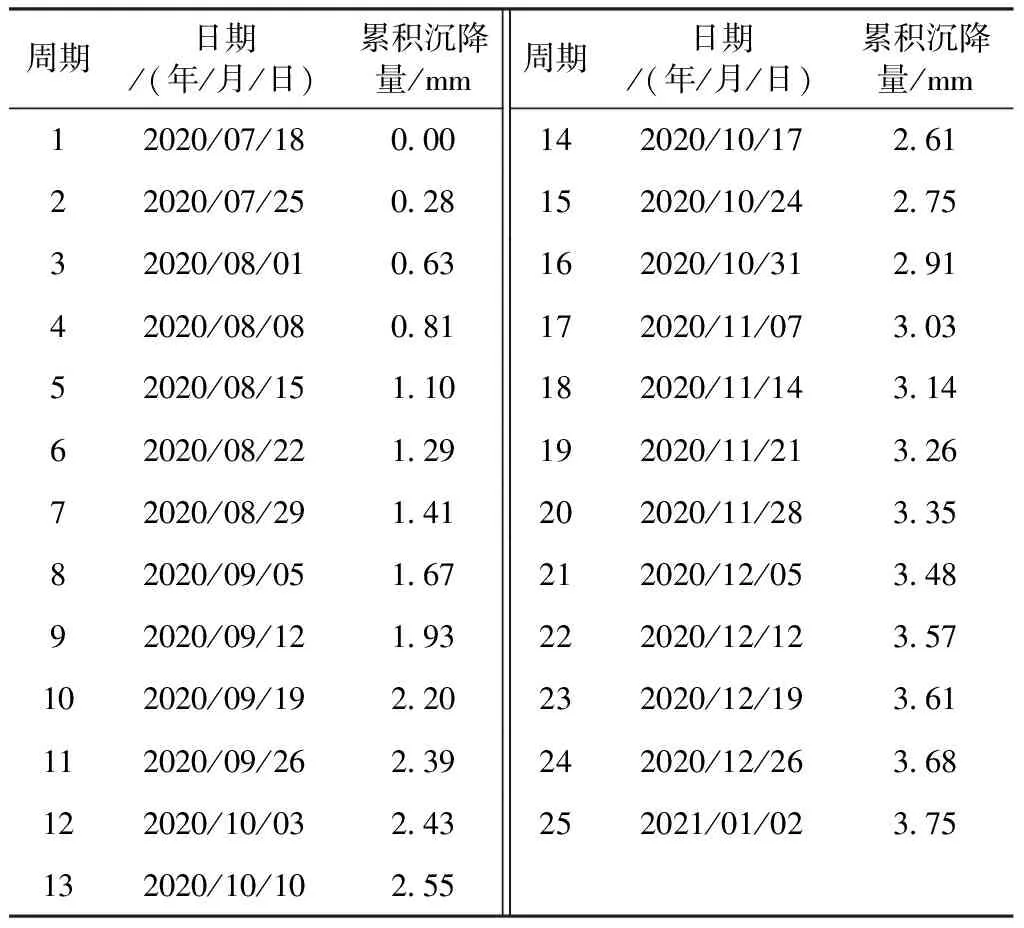
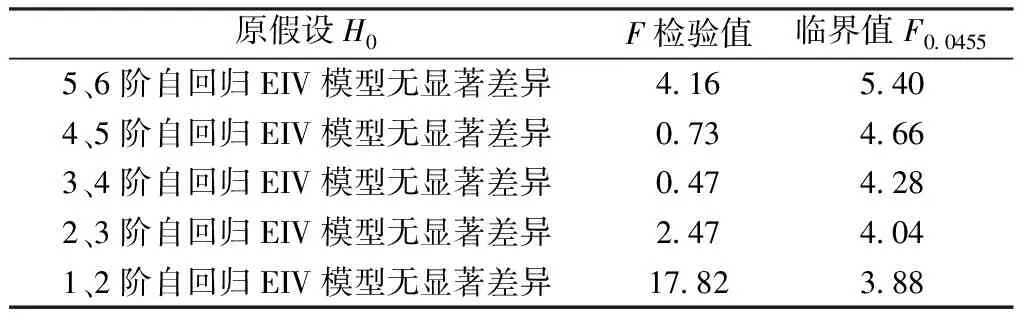
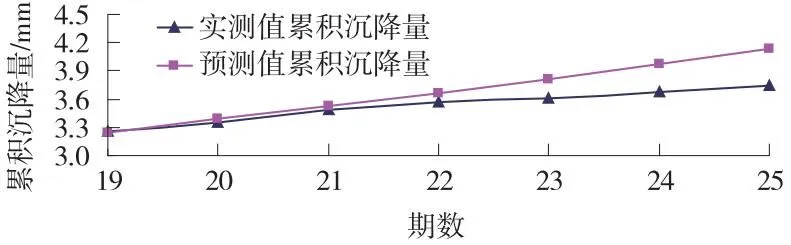
測量中常取2倍中誤差為極限誤差,在此顯著水平α取為4.55%。若F

當接受H0時,為了得到最佳的自回歸EIV模型,需要采用上述方法進一步對p-2階、p-3階…等低階模型作檢驗分析,直至i+1階、i階模型間存在顯著差異。

3 高鐵橋墩沉降預測方法

進行高鐵橋墩的沉降預報分析,關鍵是要確保所建模型能夠準確反映橋墩變形的動態特征。綜合前文分析,對有n期沉降監測高程值的高鐵橋墩沉降預測分析問題,給出一種基于自回歸EIV模型的高鐵橋墩沉降預測方法,具體步驟如下。

(1)取擬構建的自回歸EIV模型的預設擬合最高階數p=n/3。

(2)結合式(5)、式(6)建立p階自回歸EIV模型,并利用1.2節提出的方法,求得回歸系數的總體最小二乘解φp以及殘差平方和Sp。

(3)根據式(11)、式(12)建立(p-1)模型,并利用式(13)～(15)求得其回歸系數的總體最小二乘解φp-1及殘差平方和Sp-1。

(4)據式(17)構造假設檢驗統計量并進行F檢驗,若F

(5)在(p-1)階模型基礎上附加參數約束(φp-1=0)得到(p-2)階模型,利用式(13)～式(15)求得(p-2)階模型的回歸系數總體最小二乘解φp-2及殘差平方和Sp-2。根據式(17),由Sp-1和Sp-2構造假設檢驗統計量進行(p-1)、(p-2)階模型的差異性檢驗,若FFα,取(p-1)階模型為最佳高鐵橋墩沉降預測模型。

(6)基于步驟5得到的最佳高鐵橋墩沉降預測自回歸EIV模型,結合式(4),計算得到第n+1期、n+2期…橋墩沉降監測點的高程預測值。

為敘述方便,以下將基于自回歸EIV模型的高鐵橋墩沉降預測方法(prediction method of high-speed railway pier settlement based on autoregressive EIV model)簡稱為PMPS-AR-EIV法。

4 實例分析

某高速鐵路特大橋全長約9.2 km,樁基均位于W2泥巖弱風化層內,共有橋墩261個,目前正處于“等待架梁”階段。為了驗證PMPS-AR-EIV方法的應用效果,對261個橋墩的沉降監測數據進行實驗分析。考慮篇幅限制,以0009356G6墩身觀測標的沉降監測為例進行說明。該橋墩為岸上簡支梁墩,墩高11.5 m,其在“等待架梁”階段的25期沉降監測數據見表1。

表1 0009356G6墩身觀測標沉降實測數據

采用PMPS-AR-EIV方法,以前18期的數據進行橋墩沉降預測建模分析,并用后7期數據對所建模型的效果進行檢驗。建模分析結果見表2。

表2 最佳自回歸EIV模型分析結果

由表2可知,進行1階、2階自回歸EIV模型差異性檢驗時,檢驗值超出臨界值,說明2個模型間差異顯著;其他模型間的差異性檢驗F檢驗值均小于臨界值,模型間差異不顯著。由此可以得出,最佳的橋墩沉降預測模型為2階自回歸EIV模型

Hi=1.7957Hi-1-0.7853Hi-2

(18)

結合橋墩沉降監測點累積沉降量預測值計算式(式(4)),利用第19～25期數據進一步分析建立的2階自回歸EIV模型的檢驗效果。對所建模型的預測效果,可以依據橋墩預測累積沉降量與實測累積沉降量之間的差異大小來判斷,若預測值與實測值的差異較小,則說明模型的預測效果較好,反之則預測效果較差。

以預測期數為橫坐標,對應的橋墩累積沉降量為縱坐標,繪制第19～25期橋墩累積沉降量的觀測值和預測值的對比結果,見圖1。

圖1 19～25期橋墩累積沉降量觀測值與預測值比較Fig.1 Comparison between observed and predicted cumulative settlement values of bridge piers in phases 19-25

由圖1可知,采用PMPS-AR-EIV算法得到的橋墩累積沉降量預測值與實測值之間差異較小,且預測周期較短時預測值十分接近實測值,如第19～22期,其最大差異為0.1 mm;隨著預測周期的變長,預測值和實測值之間的差異呈增大的趨勢,最大差異出現在第25期,為0.39 mm。由此可見,提出的PMPS-AR-EIV算法用于高鐵橋墩沉降監測的預報分析是可行和有效的,基于其建立沉降預測自回歸EIV模型可以準確反映出時間序列的橋墩累積沉降量間的相關關系,能夠對高鐵橋墩的沉降變形趨勢作出準確預測,且其原理簡單,易于編程實現。

5 結論

(1)在顧及模型變量誤差的高階自回歸EIV模型基礎上,通過附加約束條件得到低階自回歸EIV模型,從而實現將各待選模型統一為附有參數約束的線性回歸模型,該觀點是基于線性假設法獲得,符合橋墩沉降變形動態特征的最佳自回歸EIV模型的依據。

(2)PMPS-AR-EIV算法能夠建立符合高鐵橋墩沉降變形實際的最佳自回歸EIV模型,從而可以客觀、準確地對橋墩的沉降變形趨勢作出預判,為施工建設和運營維護決策的制定提供依據。